Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модуляция и демодуляция
Содержание
- 1. Модуляция и демодуляция
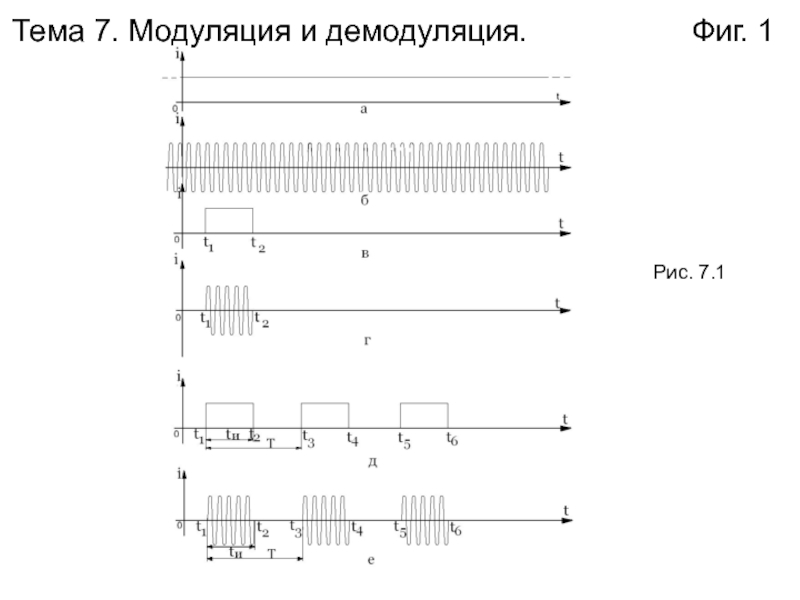
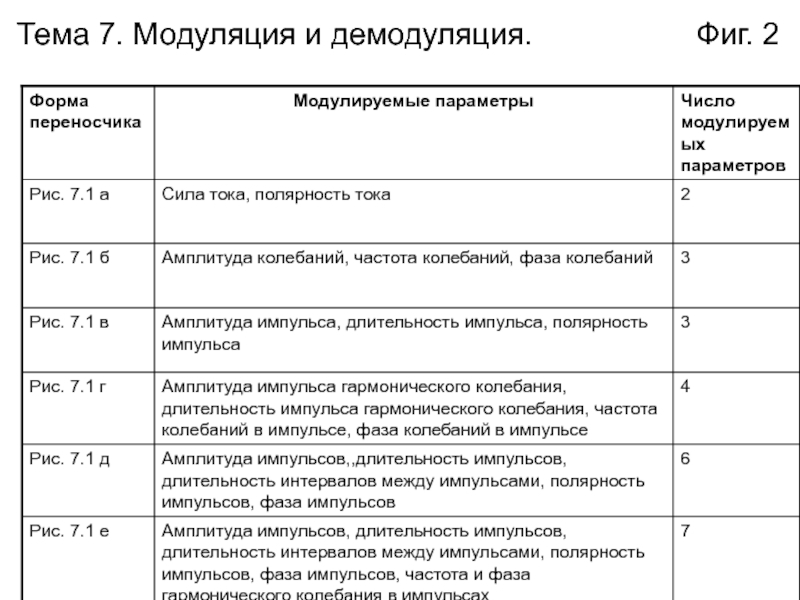
- 2. Тема 7. Модуляция и демодуляция. Фиг. 2
- 3. Тема 7. Модуляция и демодуляция.
- 4. Тема 7. Модуляция и демодуляция.
- 5. Тема 7. Модуляция и демодуляция.
- 6. Тема 7. Модуляция и демодуляция.
- 7. Тема 7. Модуляция и демодуляция.
- 8. Тема 7. Модуляция и демодуляция.
- 9. Тема 7. Модуляция и демодуляция.
- 10. Тема 7. Модуляция и демодуляция.
- 11. Тема 7. Модуляция и демодуляция.
- 12. Тема 7. Модуляция и демодуляция.
- 13. Тема 7. Модуляция и демодуляция.
- 14. Тема 7. Модуляция и демодуляция.
- 15. Тема 7. Модуляция и демодуляция.
- 16. Тема 7. Модуляция и демодуляция.
- 17. Тема 7. Модуляция и демодуляция.
- 18. Тема 7. Модуляция и демодуляция.
- 19. Тема 7. Модуляция и демодуляция.
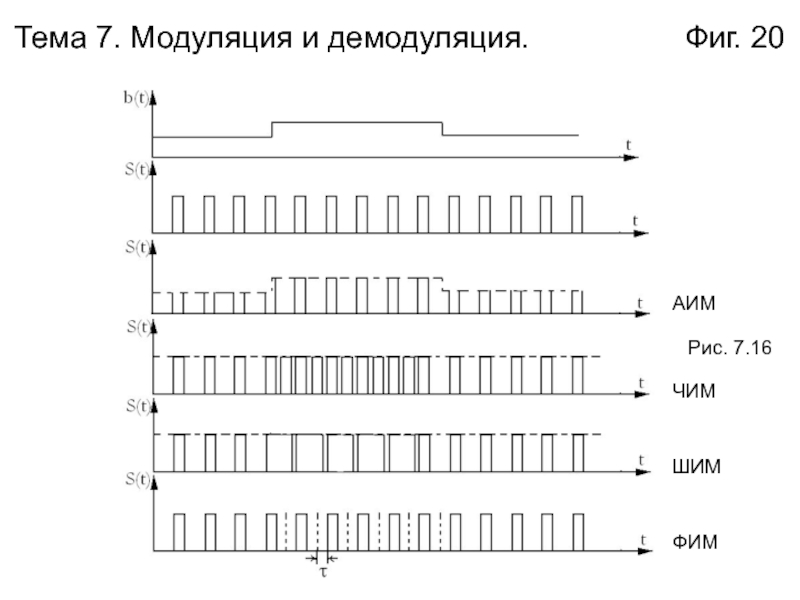
- 20. Тема 7. Модуляция и демодуляция. Фиг. 20Рис. 7.16АИМЧИМШИМФИМ
- 21. Тема 7. Модуляция и демодуляция.
- 22. Тема 7. Модуляция и демодуляция.
- 23. Тема 7. Модуляция и демодуляция.
- 24. Тема 7. Модуляция и демодуляция.
- 25. Тема 7. Модуляция и демодуляция.
- 26. Тема 7. Модуляция и демодуляция.
- 27. Скачать презентанцию
Слайды и текст этой презентации
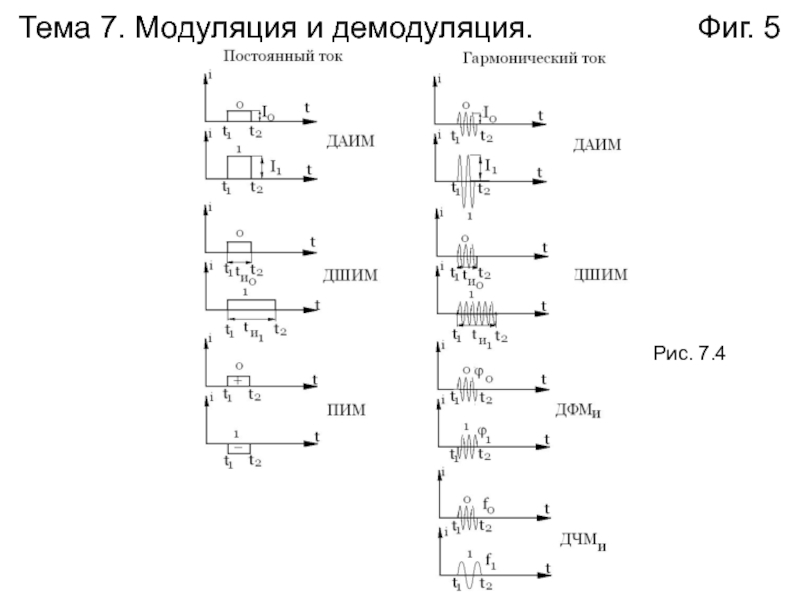
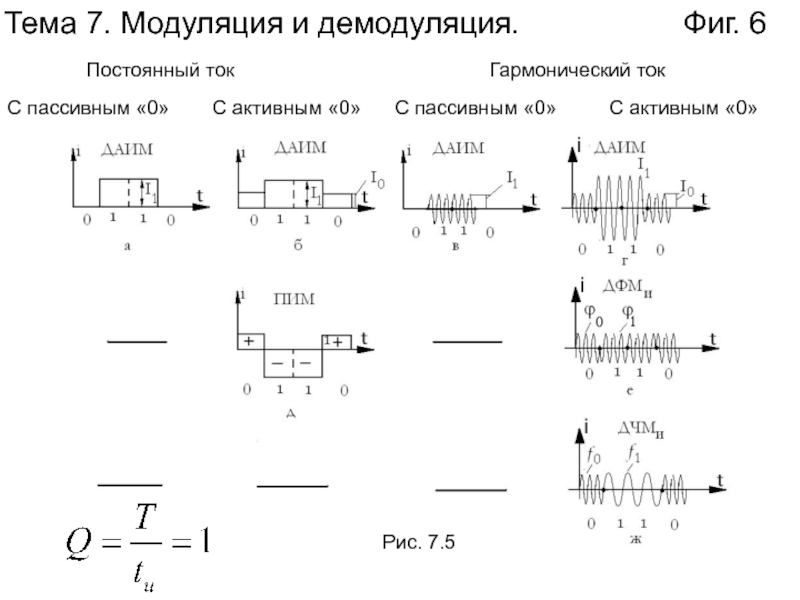
Слайд 6Тема 7. Модуляция и демодуляция.
Фиг. 6
Постоянный ток
Гармонический ток
С пассивным «0»
С
пассивным «0»С активным «0»
С активным «0»
Рис. 7.5
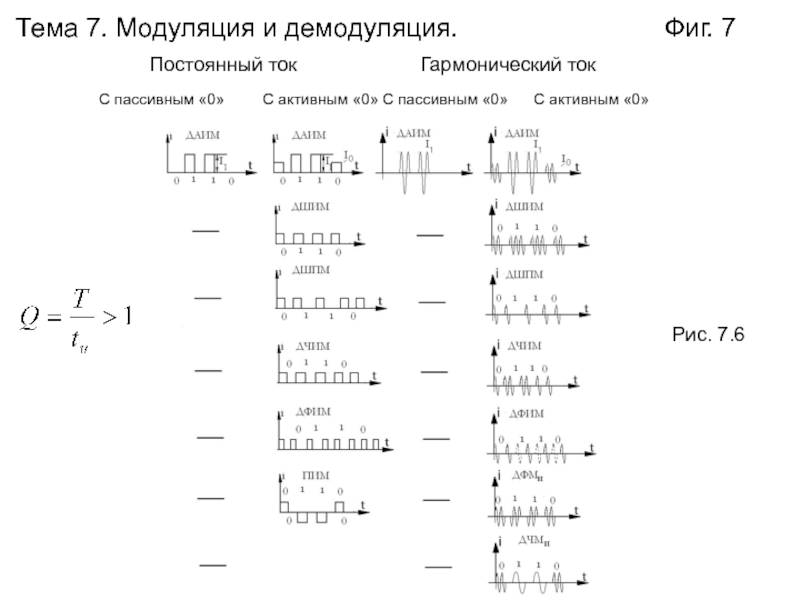
Слайд 7Тема 7. Модуляция и демодуляция.
Фиг. 7
Постоянный
токГармонический ток
С пассивным «0»
С пассивным «0»
С активным «0»
С активным «0»
Рис. 7.6
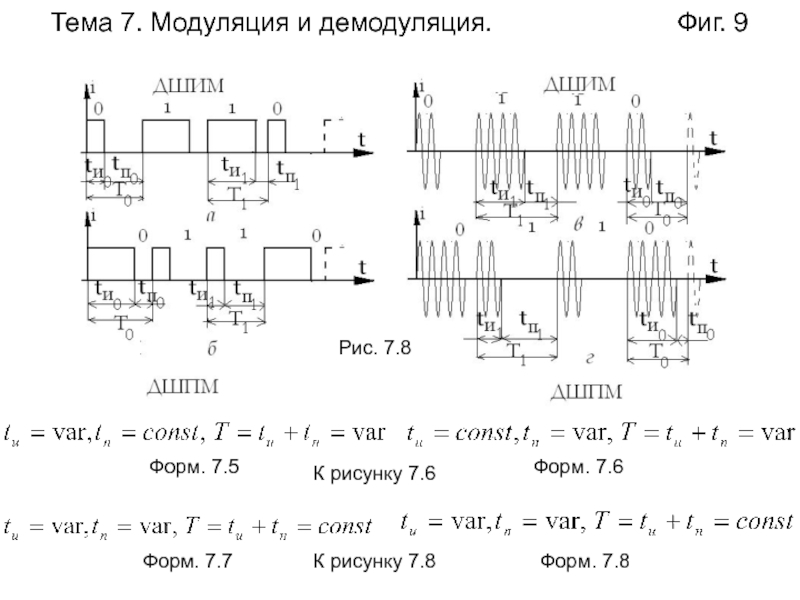
Слайд 9Тема 7. Модуляция и демодуляция.
Фиг. 9
Рис. 7.8
Форм.
7.5Форм. 7.6
Форм. 7.7
Форм. 7.8
К рисунку 7.6
К рисунку 7.8
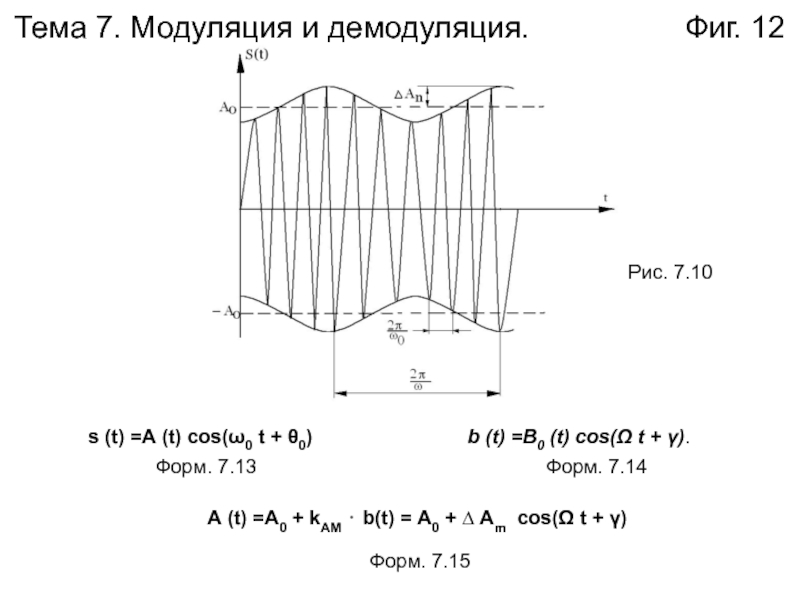
Слайд 12Тема 7. Модуляция и демодуляция.
Фиг. 12
s (t) =А (t) cos(ω0 t + θ0) b (t) =B0 (t) cos(Ω t + γ).
А (t) =А0 + kАМ ⋅ b(t) = А0 + ∆ Аm cos(Ω t + γ)
Рис. 7.10
Форм. 7.13
Форм. 7.14
Форм. 7.15
Слайд 13Тема 7. Модуляция и демодуляция.
Фиг. 13
s (t) =А0 [1 +M cos(Ω t + γ)] cos( ω0 t + θ0) А (t) =А0 [1 + М cos (Ω t + γ)]
s (t) =А0 [cos(ω0 t + θ0 ) + M cos(Ω t + γ) cos(ω0 t + θ0 )]
M cos(Ω t + γ) cos( ω0 t + θ0 ) = (М/2) cos [( ω0 + Ω ) t + (θ0 + γ) ] +
+ (М/2) cos [( ω0- Ω) t + (θ0 - γ) ]
А min = А 0 (1 - М)
А mах = А 0 (1 + М).
Форм. 7.16
Форм. 7.17
Форм. 7.18
Форм. 7.19
Форм. 7.20
Форм. 7.21
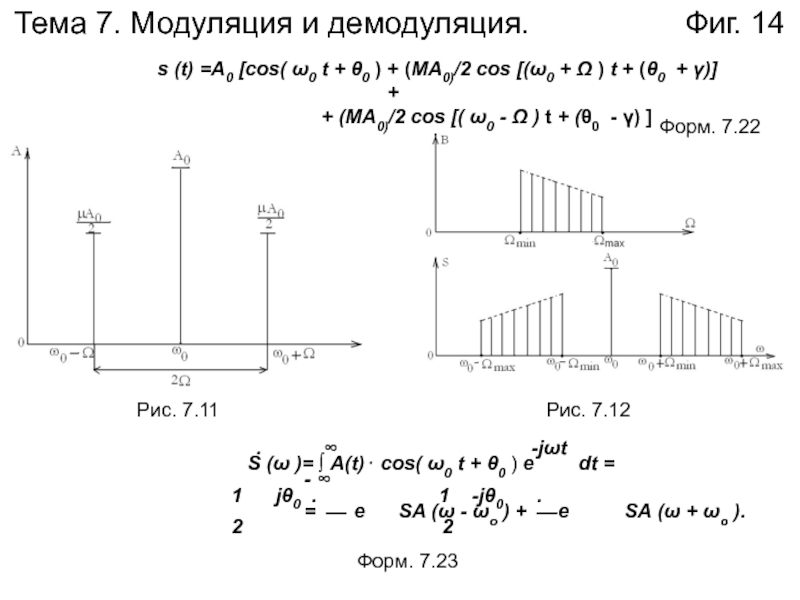
Слайд 14Тема 7. Модуляция и демодуляция.
Фиг. 14
s (t) =А0 [cos( ω0 t + θ0 ) + (МА0)/2 cos [(ω0 + Ω ) t + (θ0 + γ)] ++ (МА0)/2 cos [( ω0 - Ω ) t + (θ0 - γ) ]
. ∞ -jωt
S (ω )= ∫ А(t)⋅ cos( ω0 t + θ0 ) е dt =
- ∞
1 jθ0 . 1 -jθ0 .
= ⎯ е SA (ω - ωo ) + ⎯ е SA (ω + ωo ).
2 2
Форм. 7.22
Форм. 7.23
Рис. 7.11
Рис. 7.12
Слайд 16Тема 7. Модуляция и демодуляция.
Фиг. 16
s (t) =А0 cos( ω0 t
+ θ0 ) = А0cos ψ (t)ψ(t2) - ψ(t1) = ( ω0 t2 + θ0 ) - ( ω0 t1 + θ0 ) = ω0 (t2 - t1)
ψ(t2) - ψ(t1)
ω0 = ⎯⎯⎯⎯⎯
t2 – t1
∞
ψ(t2) - ψ(t1) = ∫ ω(t) dt,
-∞
dψ(t)
ω(t) = ⎯⎯
dt
t
ψ(t) = ∫ ω(t) dt + θ0
0
ψ(t) =ω0(t) + θ(t) +θ0
Форм. 7.24
Форм. 7.25
Форм. 7.26
Форм. 7.27
Форм. 7.28
Форм. 7.29
Форм. 7.30
Слайд 17Тема 7. Модуляция и демодуляция.
Фиг. 17
s (t) =А0 cos [ωδ t
+ θ(t) + θ0] ω(t) = ω0 +ωδ cos Ωt
t ωδ
ψ(t) = ∫ ( ω0 + ωδ cos Ωt) dt + θ0 = ω0 t + ⎯ sin Ωt + θ0
0 Ω
ωδ
s (t) =А0 cos [ω0 t + ⎯ sin Ωt + θ0]
Ω
ωд
θmaх = ⎯ = m
Ω
s (t) =А0 cos [ω0 t + θmaх sinΩt + θ0]
d
ω(t) = ⎯ (ω0 t + θmaх sinΩt + θ0) = ω0 + θmaх Ω cos Ωt.
dt
θmaх Ω = ωд
Форм. 7.31
Форм. 7.37
Форм. 7.36
Форм. 7.35
Форм. 7.34
Форм. 7.33
Форм. 7.38
Форм. 7.32
Слайд 18Тема 7. Модуляция и демодуляция.
Фиг. 18
s (t) =А0 cos (ω0 t + m sinΩt) s (t) =А0 cos (m sinΩt) cosω0 t - А0 sin (m sinΩt) sinω0 t
sin (m sinΩt) = 2J1 (m) SinΩt +
+2J3(m) sin3Ωt + 2J5(m) sin5Ωt + …
cos(m sinΩt) = J0 (m) + 2J2(m)cos2Ωt +
+ 2J4(m)cos4Ωt + …
s (t) =А0 cos (ω0 t + m sin Ωt) = А0 { J0 (m) cosω0 t +
+J1(m) [cos (ω0 + Ω)t - cos(ω0 - Ω)t] +
+J2(m) [cos (ω0 +2Ω)t - cos(ω0 - 2Ω)t] +
+J3(m) [cos (ω0 + 3Ω)t - cos(ω0 - 3Ω)t] + …}
Форм. 7.39
Форм. 7.40
Форм. 7.43
Форм. 7.41
Форм. 7.42
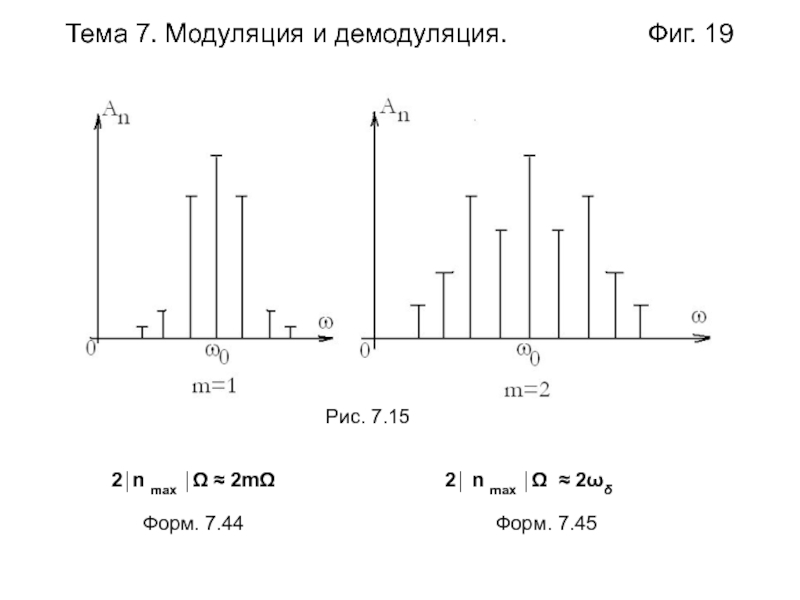
Слайд 19Тема 7. Модуляция и демодуляция.
Фиг. 19
2⏐n maх ⏐Ω ≈ 2mΩ
2⏐ n maх ⏐Ω ≈ 2ωδ
Форм. 7.44
Форм. 7.45
Рис. 7.15
Слайд 21Тема 7. Модуляция и демодуляция.
Фиг. 21
2E nω1τиАn = ⎯⎯ sin ⎯⎯⎯
πn 2
Е (t) = Е0 + ∆ Е (t)
1 ∞ jnω1t
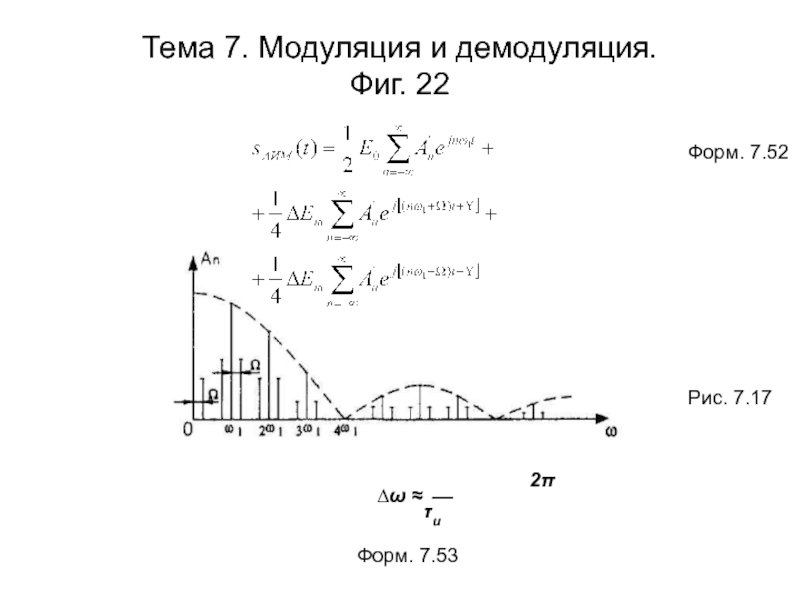
sАИМ (t) = ⎯ [Е0 + ∆ Е (t)] Σ А′ e
2 n= -∞
∆ Е (t) = ∆ Еm cos (Ωt + γ)
1 j(Ωt + γ) - j(Ωt + γ)
∆ Е (t) = ⎯ ∆ Еm [e + e ]
2
Форм. 7.46
Форм. 7.47
Форм. 7.48
Форм. 7.49
Форм. 7.50
Форм. 7.51
Слайд 23Тема 7. Модуляция и демодуляция.
Фиг. 23
s (t) = А(t)cos ψ(t)
s (t) = А0 cosω0 t
s (t) = А (t) cosω t
А0 cosω0 t = А (t) cos (ω0 + ∆ω)t
A0cosω0t
А (t) = ⎯⎯⎯⎯⎯⎯ =
cos (ω0 + ∆ω)t
A0cosω0t
= ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ =
cos ∆ωt ⋅ cosω0 t - sin ∆ωt ⋅ sin ω0 t
A0
= ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
cos ∆ωt - sin ∆ωt ⋅ tg ω0 t
Форм. 7.54
Форм. 7.55
Форм. 7.56
Форм. 7.57
Форм. 7.58
Форм. 7.59
Слайд 24Тема 7. Модуляция и демодуляция.
Фиг. 24
s1(t)ω(t) = arctg [ ⎯⎯ ]
s(t)
1 ∞ s(τ)
s1(t) = – ⎯ ∫ ⎯⎯ dτ
π -∞ τ – t
1 ∞ s1(τ)
s(t) = ⎯ ∫ ⎯⎯ dτ
π -∞ τ – t
s (t) = Σ (аn cosωn t +bn sin ωn t)
s1 (t) = Σ (аn sinωn t -bn cos ωn t)
1 ∞
s (t) = ⎯ ∫ [ а(ω) cosω t + -b(ω) sin ω t] dω
π 0
Форм. 7.60
Форм. 7.61
Форм. 7.62
Форм. 7.63
Форм. 7.64
Форм. 7.65
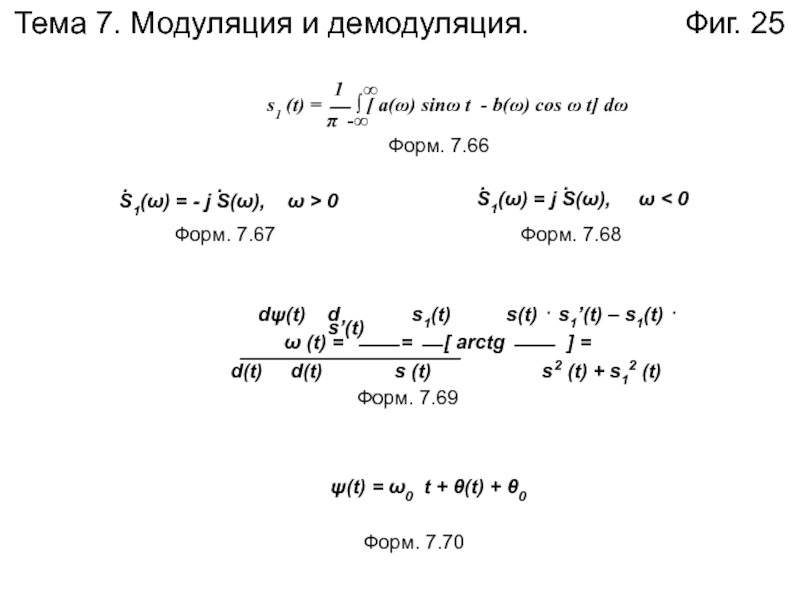
Слайд 25Тема 7. Модуляция и демодуляция.
Фиг. 25
1 ∞
s1 (t) = ⎯ ∫ [ а(ω) sinω t - b(ω) cos ω t] dωπ -∞
. .
S1(ω) = - j S(ω), ω > 0
. .
S1(ω) = j S(ω), ω < 0
dψ(t) d s1(t) s(t) ⋅ s1’(t) – s1(t) ⋅ s’(t)
ω (t) = ⎯⎯ = ⎯ [ arctg ⎯⎯ ] = ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
d(t) d(t) s (t) s2 (t) + s12 (t)
ψ(t) = ω0 t + θ(t) + θ0
Форм. 7.66
Форм. 7.67
Форм. 7.68
Форм. 7.69
Форм. 7.70
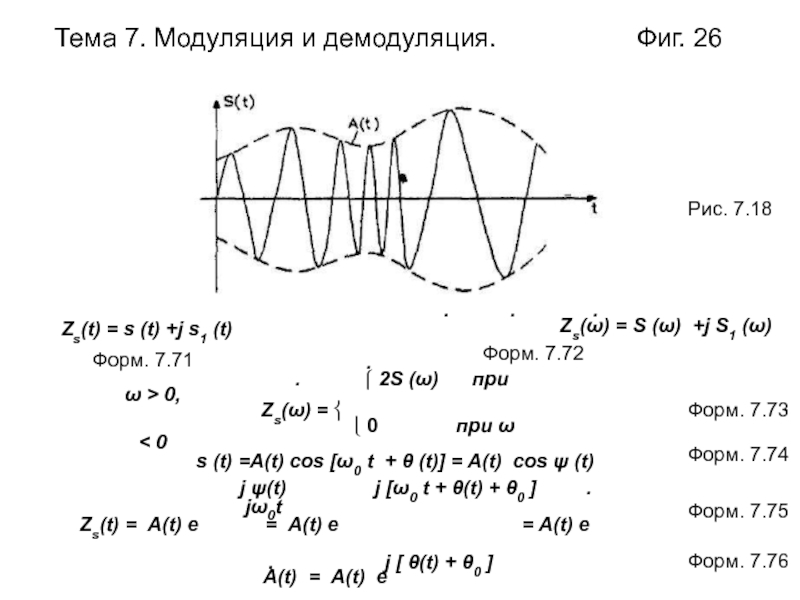
Слайд 26Тема 7. Модуляция и демодуляция.
Фиг. 26
Zs(t) = s (t) +j
s1 (t) . . .
Zs(ω) = S (ω) +j S1 (ω)
.
. . ⎧ 2S (ω) при ω > 0,
Zs(ω) = ⎨
⎩ 0 при ω < 0
s (t) =А(t) cos [ω0 t + θ (t)] = А(t) cos ψ (t)
j ψ(t) j [ω0 t + θ(t) + θ0 ] . jω0t
Zs(t) = А(t) е = А(t) е = А(t) е
. j [ θ(t) + θ0 ]
А(t) = А(t) е
Форм. 7.71
Форм. 7.72
Форм. 7.73
Форм. 7.74
Форм. 7.75
Форм. 7.76
Рис. 7.18