Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Молекулярно-кинетическая теория
Содержание
- 1. Молекулярно-кинетическая теория
- 2. Молекулярная физикаМолекулярная физика – раздел физики, изучающий физические свойства вещества на основе рассмотрения его молекулярного строения
- 3. Основные положения МКТ:1. Все тела – твердые,
- 4. МолекулаМолекула – наименьшая частица вещества, определяющая все
- 5. Вероятностный метод в молекулярной физикеМолекулярная физика пользуется
- 6. 2. Масса и размеры молекулЛЕКЦИЯ 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА
- 7. Атомная единица массы (а.е.м)Атомная единица массы (а.е.м)
- 8. Относительная атомная массаОтносительной атомной массой Ar химического
- 9. Относительная молекулярная массаОтносительной молекулярной массой Mr вещества называется отношение массы молекулы этого вещества к 1 а.е.м.
- 10. Количество веществаМоль (единица измерения количества вещества в
- 11. Число АвогадроЧисло Авогадро NA – число частиц а одном моле вещества:
- 12. Молярная массаМолярной массой M называется масса одного
- 13. 3. Модель идеального газаЛЕКЦИЯ 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА
- 14. Идеальный газИдеальным газом называется газ, молекулы которого:не
- 15. Уравнение состояния идеального газаУравнение состояния идеального газа (уравнение Менделеева – Клапейрона):
- 16. Уравнение состояния идеального газа
- 17. Закон АвогадроВ одинаковых объемах идеальных газов при
- 18. Плотность идеального газа
- 19. Закон ДальтонаДавление смеси идеальных газов равно сумме
- 20. Уравнение состояния для смеси идеальных газов
- 21. 4. Основное уравнение молекулярно-кинетической теорииЛЕКЦИЯ 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА
- 22. Основное уравнение МКТОсновное уравнение молекулярно-кинетической теории газов
- 23. Предположения, при которых получено основное уравнение МКТ:Газ
- 24. 5. Распределение энергии по степеням свободы молекулЛЕКЦИЯ 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА
- 25. Число степеней свободыЧислом степеней свободы механической системы
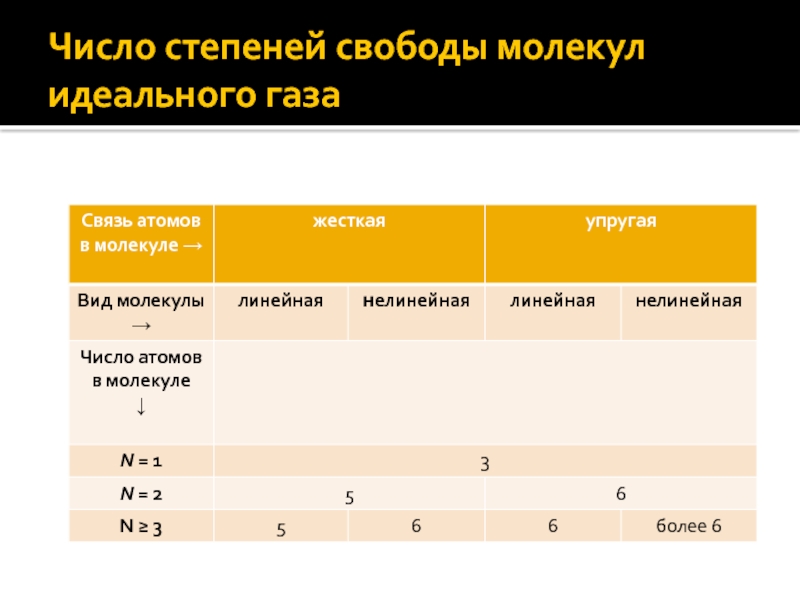
- 26. Число степеней свободы молекул идеального газа
- 27. Закон БольцманаЗакон Больцмана (закон равнораспределения энергии по
- 28. Упругая молекула (молекула, атомы которой совершают колебания),
- 29. Эффективное число степеней свободы
- 30. Средняя энергия одной молекулы и N молекул
- 31. Скачать презентанцию
Молекулярная физикаМолекулярная физика – раздел физики, изучающий физические свойства вещества на основе рассмотрения его молекулярного строения
Слайды и текст этой презентации
Слайд 11. Основные положения молекулярно-кинетической теории вещества
ЛЕКЦИЯ 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА
Слайд 2Молекулярная физика
Молекулярная физика – раздел физики, изучающий физические свойства вещества
на основе рассмотрения его молекулярного строения
Слайд 3Основные положения МКТ:
1. Все тела – твердые, жидкие, газообразные –
состоят из атомов и молекул.
2. Молекулы всех тел находятся в
беспорядочном хаотическом движении, не имеющем какого-либо выбранного направления; такое движение называется тепловым, т.к. его скорость зависит от температуры вещества.
Слайд 4Молекула
Молекула – наименьшая частица вещества, определяющая все его химические свойства;
молекула состоит из атомов.
Атом – наименьшая частица химического элемента, способная
к самостоятельному существованию и являющаяся носителем его индивидуальных свойств.
Слайд 5Вероятностный метод в молекулярной физике
Молекулярная физика пользуется вероятностными (статистическими) методами
и объясняет наблюдаемые на опыте свойства тел суммарным результатом действия
отдельных молекул; поэтому молекулярная физика часто называется статистической физикой
Слайд 7Атомная единица массы (а.е.м)
Атомная единица массы (а.е.м) – единица измерения
массы атомов и молекул.
1 а.е.м. называется масса, равная 1/12
массы атома 12С (изотопа углерода с массовым числом 12):1 а.е.м. = 1,66 ⋅ 10-27 кг
Слайд 8Относительная атомная масса
Относительной атомной массой Ar химического элемента называется отношение
массы атома этого элемента к 1 а.е.м.
Слайд 9Относительная молекулярная масса
Относительной молекулярной массой Mr вещества называется отношение массы
молекулы этого вещества к 1 а.е.м.
Слайд 10Количество вещества
Моль (единица измерения количества вещества в МКТ) – количество
вещества, в котором содержится столько структурных единиц (атомов, молекул, ионов,
кластеров, электронов и т.д.), сколько атомов содержится в 12 г изотопа углерода 12С.
Слайд 12Молярная масса
Молярной массой M называется масса одного моля вещества:
Молярная масса,
выраженная в граммах на моль, численно равна относительной молекулярной массе:
M = Mr (г/моль)
Слайд 14Идеальный газ
Идеальным газом называется газ, молекулы которого:
не взаимодействуют друг с
другом на расстоянии (при столкновении друг с другом и со
стенками сосуда молекул ведут себя как абсолютно упругие шары).Собственный объем молекул газа ничтожно мал по сравнению с объемом сосуда, в котором находится газ.
Слайд 15Уравнение состояния идеального газа
Уравнение состояния идеального газа (уравнение Менделеева –
Клапейрона):
Слайд 17Закон Авогадро
В одинаковых объемах идеальных газов при одинаковых температурах и
давлении содержится одно и то же число молекул (верно и
обратное утверждение: различные газы, содержащие одинаковое число молекул, при одинаковых температуре и давлении занимают одинаковые объемы).В частности, при нормальных условиях
(T0 = 273,15 K, p0 = 1,0132 ⋅ 105 Па) 1 моль любого газа занимает объем Vm = 22,415 ⋅ 10-3 м3
Слайд 19Закон Дальтона
Давление смеси идеальных газов равно сумме парциальных давлений этих
газов:
Парциальным давлением компоненты газовой смеси называется давление, которые производила бы
она, если бы занимала весь объем смеси в отсутствии других компонентПри этом каждая и газовая компонента смеси подчиняется уравнению Менделеева – Клапейрона.
Слайд 214. Основное уравнение молекулярно-кинетической теории
ЛЕКЦИЯ 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА
Слайд 22Основное уравнение МКТ
Основное уравнение молекулярно-кинетической теории газов связывает давление p,
оказываемое газом на стенки сосуда, со средней кинетической энергией поступательного
движения молекулы <εпост>:
Слайд 23Предположения, при которых получено основное уравнение МКТ:
Газ находится в состоянии
термодинамического равновесия со стенками сосуда; давление газа не зависит от
формы и размеров сосуда.Взаимодействие молекул со стенками сосуда описывается моделью упругих соударений с зеркальным отражением.
Все направления движения молекул равновероятны.
Слайд 245. Распределение энергии по степеням свободы молекул
ЛЕКЦИЯ 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ
ВЕЩЕСТВА
Слайд 25Число степеней свободы
Числом степеней свободы механической системы называется число независимых
величин, полностью определяющих положение системы в пространстве.
Степени свободы молекул идеального
газа могут быть поступательными (т. е. соответствовать поступательному движению), вращательными и колебательными
Слайд 27Закон Больцмана
Закон Больцмана (закон равнораспределения энергии по степеням свободы): в
состоянии теплового равновесия на каждую степень свободы в среднем приходится
одинаковая энергия, равная (½)kT
Слайд 28Упругая молекула (молекула, атомы которой совершают колебания), обладает как кинетической,
так и потенциальной энергией, связанной с колебаниями, поэтому колебательная степень
свободы характеризуется удвоенной энергетической емкостью: средняя энергия, приходящаяся на колебательную степень свободы, равна kT (по (1/2)kT на кинетическую и на потенциальную энергии колебаний)
