Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МОУ Высокоярская сош Бакчарского района Томской области Теорема Пифагора: вне
Содержание
- 1. МОУ Высокоярская сош Бакчарского района Томской области Теорема Пифагора: вне
- 2. Слайд 2
- 3. Цели и задачи:Кто на самом деле открыл
- 4. Из истории теоремы Пифагора Древний КитайМатематическая книга
- 5. Теорема Пифагора у древних египтянКантор (крупнейший немецкий
- 6. Теорема в Вавилонии«Заслугой первых греческих математиков, таких
- 7. У индусовГеометрия у индусов, как и у
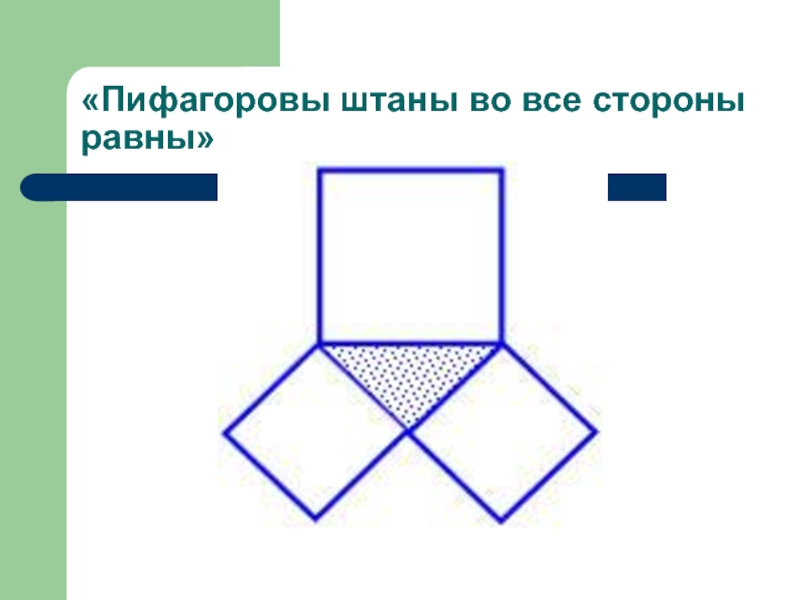
- 8. «Пифагоровы штаны во все стороны равны»
- 9. В течение двух тысячелетий наиболее распространенным доказательством
- 10. Рисунки учащихся средних веков
- 11. ПРОСТЕЙШИЕ ДОКАЗАТЕЛЬСТВА Простейшее доказательство теоремы получается в простейшем
- 12. Доказательство 9 века н.э.На рисунке квадраты, построенные
- 13. Доказательство Перигаля.В учебниках нередко встречается разложение указанное
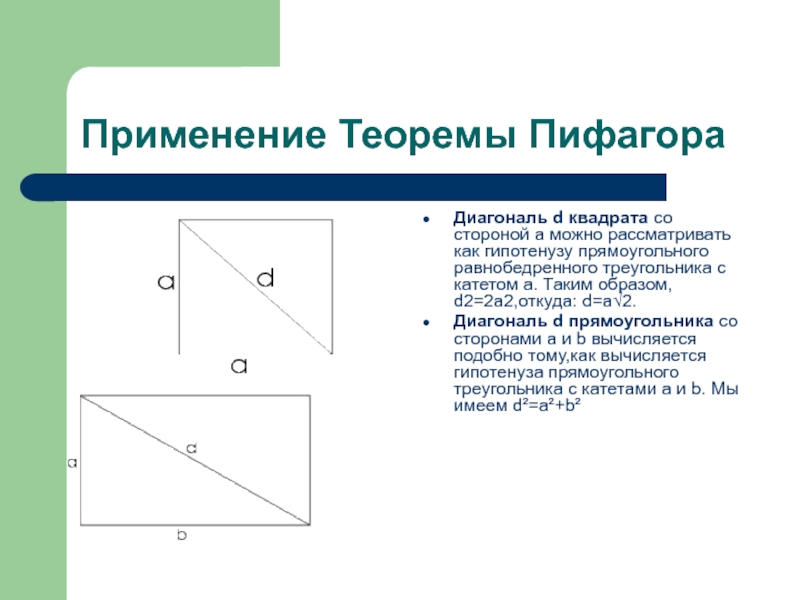
- 14. Применение Теоремы ПифагораДиагональ d квадрата со стороной
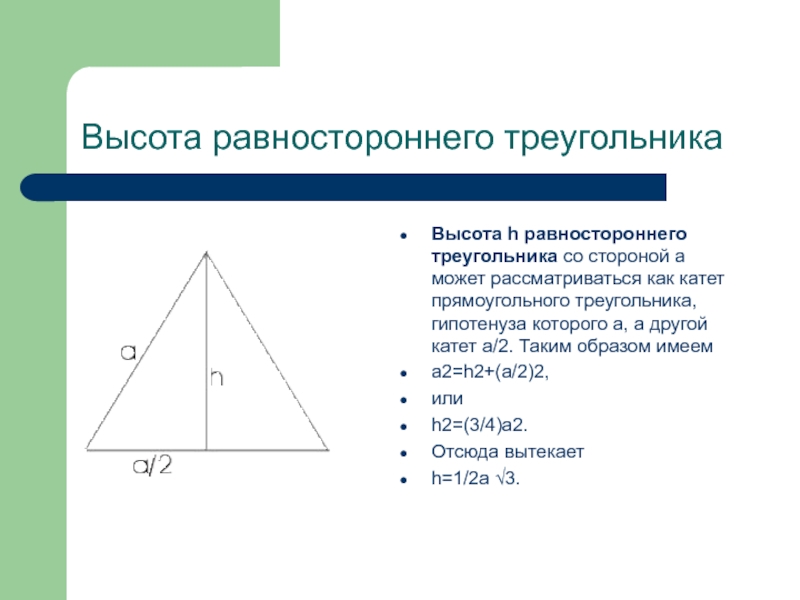
- 15. Высота равностороннего треугольника Высота h равностороннего треугольника
- 16. На рисунке изображен куб, внутри которого проведена
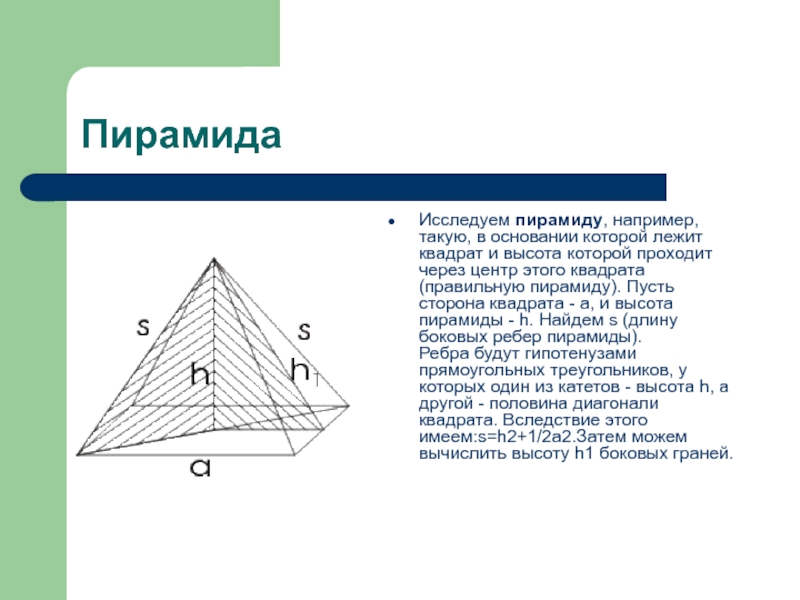
- 17. ПирамидаИсследуем пирамиду, например, такую, в основании которой
- 18. Готические и Романские стили
- 19. Послание марсианам в виде теоремы Пифагора
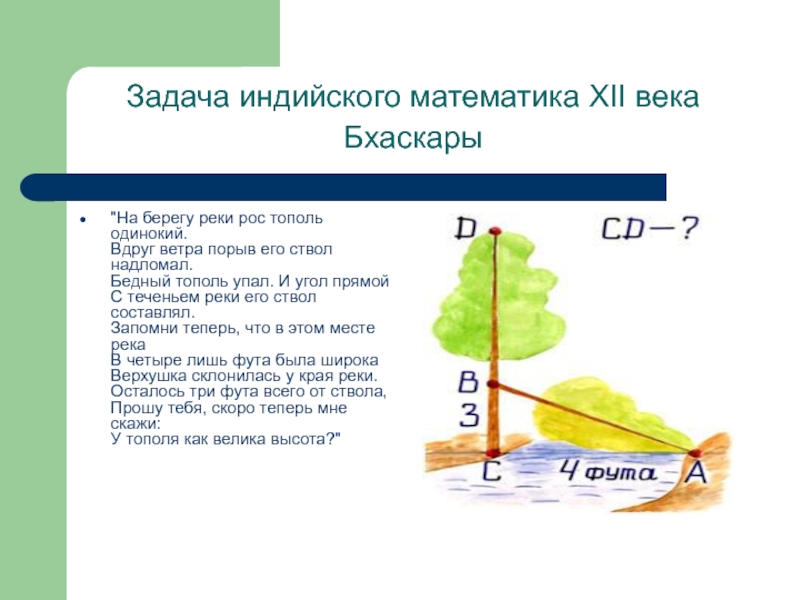
- 20. Задача индийского математика XII века Бхаскары "На
- 21. Задача из китайской "Математики в девяти
- 22. Задача из учебника "Арифметика" Леонтия Магницкого«Случится
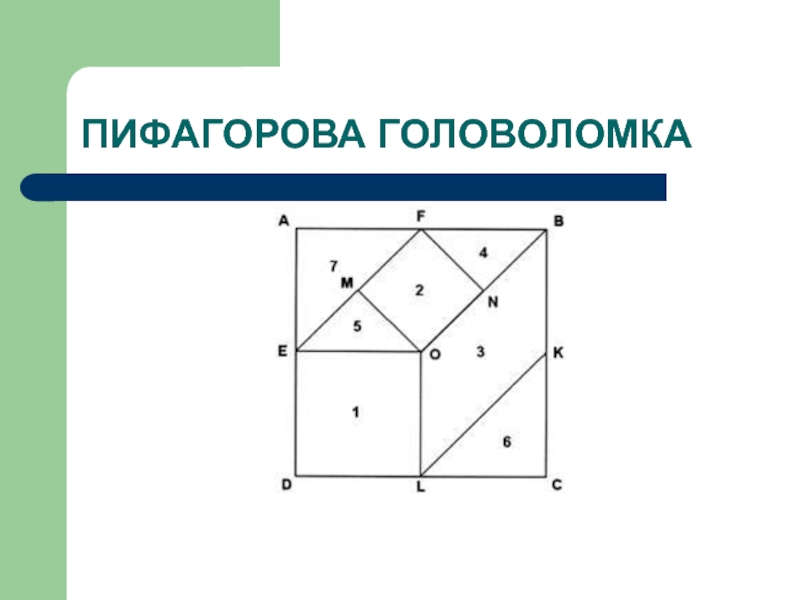
- 23. ПИФАГОРОВА ГОЛОВОЛОМКА
- 24. Учебное исследование по теме "Теорема Пифагора"Задача.
- 25. Скачать презентанцию
Цели и задачи:Кто на самом деле открыл теорему?Почему она долгое время называлась «теоремой невесты»?Почему «пифагоровы штаны во все стороны равны»?Существуют ли другие доказательства теоремы?Как используется теорема Пифагора в решении задач; в
Слайды и текст этой презентации
Слайд 1МОУ «Высокоярская сош» Бакчарского района Томской области Теорема Пифагора: вне
урока.
Васильевна, учитель физики и математикиСлайд 3Цели и задачи:
Кто на самом деле открыл теорему?
Почему она долгое
время называлась «теоремой невесты»?
Почему «пифагоровы штаны во все стороны равны»?
Существуют
ли другие доказательства теоремы?Как используется теорема Пифагора в решении задач; в искусстве?
Поиск исторических задач на теорему Пифагора
Слайд 4Из истории теоремы Пифагора
Древний Китай
Математическая книга Чу-пей:
"Если прямой угол разложить
на составные части, то линия, соединяющая концы его сторон, будет
5, когда основание есть 3, а высота 4".Слайд 5Теорема Пифагора у древних египтян
Кантор (крупнейший немецкий историк математики) считает,
что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300
г. до н. э., во времена царя Аменемхета(согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.Слайд 6Теорема в Вавилонии
«Заслугой первых греческих математиков, таких как Фалес, Пифагор
и пифагорейцы, является не открытие математики, но ее систематизация и
обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку."Слайд 7У индусов
Геометрия у индусов, как и у египтян и вавилонян,
была тесно связана с культом. Весьма вероятно, что теорема о
квадрате гипотенузы была известна в Индии уже около 18 века до н. э.Слайд 9В течение двух тысячелетий наиболее распространенным доказательством теоремы Пифагора было
придуманное Евклидом. Оно помещено в его знаменитой книге «Начала».
Евклид
опускал высоту СН из вершины прямого угла на гипотенузу и доказывал, что её продолжение делит достроенный на гипотенузе квадрат на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах.Чертёж, применяемый при доказательстве этой теоремы, в шутку называют «пифагоровы штаны». В течение долгого времени он считался одним из символов математической науки.
Слайд 11ПРОСТЕЙШИЕ ДОКАЗАТЕЛЬСТВА
Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного
треугольника. В самом деле, достаточно просто посмотреть на мозаику равнобедренных
прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Например, для треугольника ABC : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,- по дваСлайд 12Доказательство 9 века н.э.
На рисунке квадраты, построенные на катетах, размещены
ступенями один рядом с другим. Эту фигуру, которая встречается в
доказательствах, датируемых не позднее, чем 9 столетием н. э., индусы называли "стулом невесты".Слайд 13Доказательство Перигаля.
В учебниках нередко встречается разложение указанное на рисунке (так
называемое "колесо с лопастями"; это доказательство нашел Перигаль). Через центр
O квадрата, построенного на большем катете, проводим прямые, параллельную и перпендикулярную гипотенузе. Соответствие частей фигуры хорошо видно из чертежаСлайд 14Применение Теоремы Пифагора
Диагональ d квадрата со стороной а можно рассматривать
как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом,
d2=2a2,откуда: d=а√2.Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому,как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем d²=a²+b²
Слайд 15Высота равностороннего треугольника
Высота h равностороннего треугольника со стороной а
может рассматриваться как катет прямоугольного треугольника, гипотенуза которого а, а
другой катет a/2. Таким образом имеемa2=h2+(a/2)2,
или
h2=(3/4)a2.
Отсюда вытекает
h=1/2а √3.
Слайд 16На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся
одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат
ребро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна а √2. Отсюда имеемd2=a2+2a2, d2=3a2, d=a√3.
Слайд 17Пирамида
Исследуем пирамиду, например, такую, в основании которой лежит квадрат и
высота которой проходит через центр этого квадрата (правильную пирамиду). Пусть
сторона квадрата - а, и высота пирамиды - h. Найдем s (длину боковых ребер пирамиды). Ребра будут гипотенузами прямоугольных треугольников, у которых один из катетов - высота h, а другой - половина диагонали квадрата. Вследствие этого имеем:s=h2+1/2a2.Затем можем вычислить высоту h1 боковых граней.Слайд 20Задача индийского математика XII века Бхаскары
"На берегу реки рос
тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И
угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?"Слайд 21Задача из китайской
"Математики в девяти книгах"
"Имеется водоем со стороной
в 1 чжан = 10 чи. В центре его растет
камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его.Спрашивается: какова глубина воды и какова длина камыша?"
Слайд 22Задача из учебника "Арифметика"
Леонтия Магницкого
«Случится некому человеку к стене
лестницу прибрати, стены же тоя высота есть 117 стоп. И
обретете лестницу долготью 125 стоп.И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать»
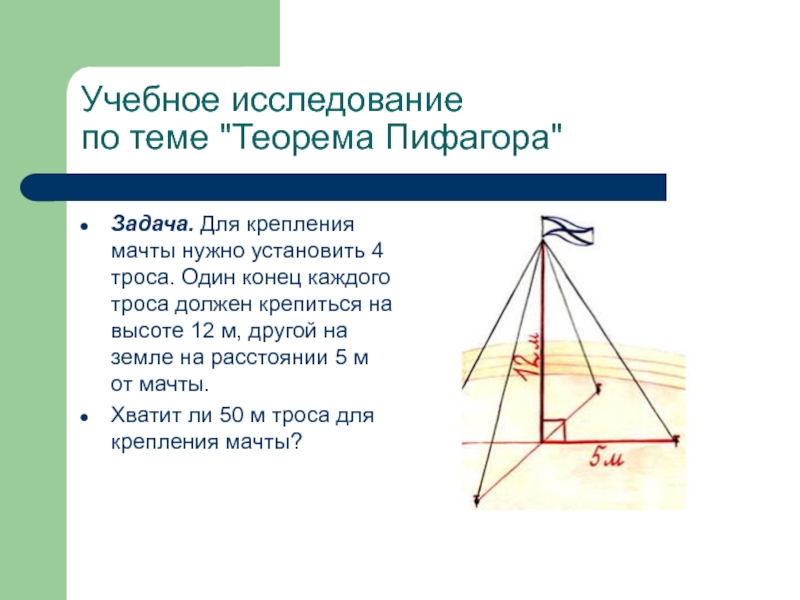
Слайд 24Учебное исследование
по теме "Теорема Пифагора"
Задача. Для крепления мачты нужно
установить 4 троса. Один конец каждого троса должен крепиться на
высоте 12 м, другой на земле на расстоянии 5 м от мачты.Хватит ли 50 м троса для крепления мачты?