Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
№ 6 дәріс
Содержание
- 1. № 6 дәріс
- 2. Болжам: F(t) және Fв(t) тарату функциялары бұрынғы
- 3. Тоқтап қалу және қалпына келу ағымдарыҚалпына келетін
- 4. Тоқтап қалу жоқ болғанда жұмысқа қабілеттілігінің мүмкіндігі
- 5. Фвi(t) қалпына келудің i тарату функциясының аяқталу уақыты бойынша
- 6. Бір уақыт аралығындағы аяқталған қалпына келу циклінің
- 7. Қалпына келудің тұрақты процессі үшін Блекуэлланың шектік
- 8. Ф’в1(s)=s2F(s)Fв(s)=/[(s+)(s+)]Ф’в2(s)=s2Ф2(s)Fв(s)=s2Ф’в1(s)F(s)Fв(s);
- 9. Слайд 9
- 10. Ауыспалы мүмкіндік әдісі 1- Жұмыс істеу қабілеттілігі;
- 11. і уақыт аралығынан кейін кез келген жағдайда
- 12. Слайд 12
- 13. Скачать презентанцию
Болжам: F(t) және Fв(t) тарату функциялары бұрынғы тоқтап қалу және қалпына келу сандарына тәуелді емес болып саналады (алмасатын қалпына келу).Егер қалпына келу қорытындысы бойынша жүйенің қасиеті бастапқы деңгейде сақталса, онда бұл
Слайды и текст этой презентации
Слайд 2Болжам: F(t) және Fв(t) тарату функциялары бұрынғы тоқтап қалу және
қалпына келу сандарына тәуелді емес болып саналады (алмасатын қалпына келу).
қалпына келу қорытындысы бойынша жүйенің қасиеті бастапқы деңгейде сақталса, онда бұл процесс регенииривті деп аталады.
Слайд 3Тоқтап қалу және қалпына келу ағымдары
Қалпына келетін жүйенің жұмыс істеу
диаграммасы
t1=T1; t2=T1+Tв1+ T2+…; ti=T1+Tв1+ T2+… + Ti; tв0=0; tв1=T1+Tв1; tвi=T1+Tв1+
T2+… + Tвi; Фi(t) и Фвi(t)
Слайд 4Тоқтап қалу жоқ болғанда жұмысқа қабілеттілігінің мүмкіндігі Po(t) i+1 тоқтап қалу
болмаған жағдайда, t моментіне і қалпына келуінің аяқталу мүмкіндігі Pi(t)
Слайд 6Бір уақыт аралығындағы аяқталған қалпына келу циклінің саны
, где
’=M[T+Tв] = +в, с учетом 6.1
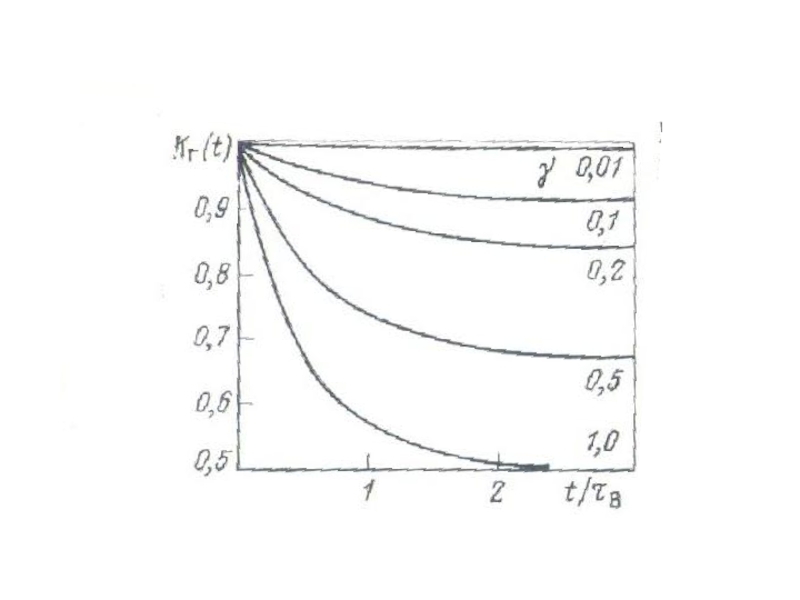
kг=limKг(t)=/(+в)
Слайд 7Қалпына келудің тұрақты процессі үшін Блекуэлланың шектік теоремасын қолданып, аламыз
Бір
уақыт аралығында t
lim[W(t+t) – W(t)]=t/(M[T]+M[Tв])=t/(+в);
Мұндағы w=1/(+в)=kг/
Лаплас бойынша пайдалану кезінде
тоқтаусыз жұмыс істеу уақытын бөлу және қалпына келу былай суреттеледі:F(s)= (1-e -t) e –st dt=/s(s+ );
Fв(s)= (1-e -t) e –st dt=/s(s+ );
![Қалпына келудің тұрақты процессі үшін Блекуэлланың шектік теоремасын қолданып, аламызБір уақыт аралығында t lim[W(t+t) – W(t)]=t/(M[T]+M[Tв])=t/(+в);Мұндағы w=1/(+в)=kг/Лаплас](/img/thumbs/a68a5af30dfb831ac5df92b7e3d13900-800x.jpg "№ 6 дәріс Қалпына келудің тұрақты процессі үшін Блекуэлланың шектік теоремасын қолданып, аламызБір уақыт")
![Ф’в1(s)=s2F(s)Fв(s)=/[(s+)(s+)]Ф’в2(s)=s2Ф2(s)Fв(s)=s2Ф’в1(s)F(s)Fв(s);](/img/tmb/3/233815/30eafbab68fdcfb45905247ef5d1c02e-800x.jpg "№ 6 дәріс Ф’в1(s)=s2F(s)Fв(s)=/[(s+)(s+)]Ф’в2(s)=s2Ф2(s)Fв(s)=s2Ф’в1(s)F(s)Fв(s);")
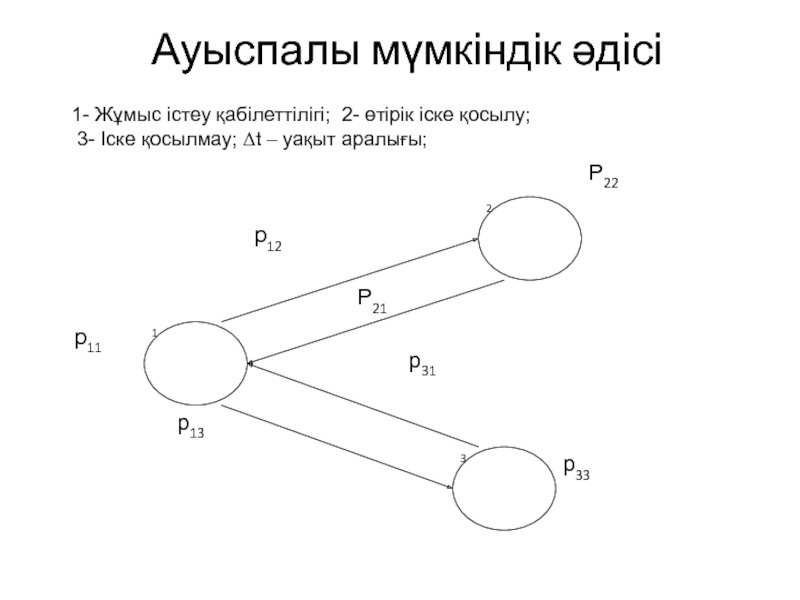
Слайд 10Ауыспалы мүмкіндік әдісі
1- Жұмыс істеу қабілеттілігі; 2- өтірік іске қосылу;
3- Іске қосылмау; t – уақыт аралығы;
Слайд 11і уақыт аралығынан кейін кез келген жағдайда жүйенің табу мүмкіндігі:
P1(i)
=p11*P1(i-1)+p12*P2(i-1)+p31*P3(i-1);
P2(i) = p12*P1(i-1)+p22*P2(i-1);
P3(i) = p13*P1(i-1)+p33*P3(i-1);
Кез келген сан аралығынан кейін:
P1(i) +
P2(i) + P3(i) =1;Бастапқы жағдай:
P1(0) =1; P2(0) = P3(0) =0;
i-аралықтан кейін жүйені табу мүмкіндігі j жағдайында мына формула бойынша есептеледі:
Pj(i) =M(0)*Mi*Dj;
M(0)= P1(0) P2(0) P3(0) ;
Слайд 12
1i
2i 3i0 1(i-1) p11 p12 p13
Dj= 1 ; M= 2(i-1) p21 p22 0
0 3(i-1) p31 0 p33
M –ауысудың матрицасы
Dj –талданатын жағдайдың векторлық бағаны
