Слайд 1НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ
Слайд 2Метрические характеристики графа
Длина маршрута v0v1…vn равна п, т. е. количеству
ребер в нем.
Длина цепи v0v1…vn равна п, т. е.
количеству ребер в ней.
Обхват графа G — это длина кратчайшего простого цикла графа G (если он есть). Это понятие не определено в случае, когда в G нет циклов.
Окружение графа G — это длина самого длинного простого цикла графа G (если он есть). Это понятие не определено в случае, когда в G нет циклов.
Слайд 3Расстояние
Расстоянием d(u, v) между двумя вершинами и и v графа
G называется длина кратчайшей простой цепи, соединяющей их; если и
и v не соединены, то полагаем d(u, v) = . В связном графе расстояние является метрикой, т.е. удовлетворяет следующим аксиомам (аксиомам метрики): для любых трех вершин и, v и w
d(u, v) 0 и d(u, v) = 0 тогда и только тогда, когда u = v;
d(u, v) = d(v, u);
d(u, v) + d(v, w) d(u, w)
Кратчайшая простая (u-v)-цепь часто называется геодезической.
Слайд 4Эксцентриситет вершины графа — расстояние до максимально удаленной от него
вершины.
Радиус графа — минимальный эксцентриситет вершин.
Диаметр d(G) связного графа G
— максимальный эксцентриситет вершин, иначе, это длина самой длинной геодезической.
Центр графа образуют вершины, у которых эксцентриситет равен радиусу. Центр графа может состоять из одной, нескольких или всех вершин графа.
Периферийные вершины имеют эксцентриситет, равный диаметру.
Простая цепь с длиной, равной диаметру, называется диаметральной.
Медиана графа — это такая его вершина, расстояние от которой до всех остальных вершин графа минимально.
Слайд 5Нагруженные (взвешенные) графы
Будем рассматривать ориентированные графы G = V, E, дугам которых приписаны
веса. Это означает, что каждой дуге u, v E поставлено
в соответствие некоторое вещественное число a (u, v), называемое весом данной дуги.
Полагаем, кроме того, a (u, v) = , если u и v не связаны дугой.
Если последовательность вершин v0, v1,..., vp определяет путь в G, то его длина определяется как сумма
Слайд 6Кратчайшие пути
Принцип оптимальности Беллмана: если ищется кратчайший путь между двумя
точками, то длина пути между любыми двумя точками кратчайшего пути
тоже будет минимальна
Слайд 7Нахождение кратчайшего пути между фиксированными вершинами s, t V
Данные:
Расстояния D[v] от фиксированной вершины s до всех остальных вершин
v V, фиксированная вершина t, матрица весов ребер, A[u, v], u, v V.
Результаты: СТЕК содержит последовательность вершин, определяющую кратчайший путь из s в t.
begin
CTEK := ; CTEK t; v:= t;
while v s do
begin
u := вершина, для которой D[v] = D[u] + A[u, v];
CTEK u;
v:= u
end
end.
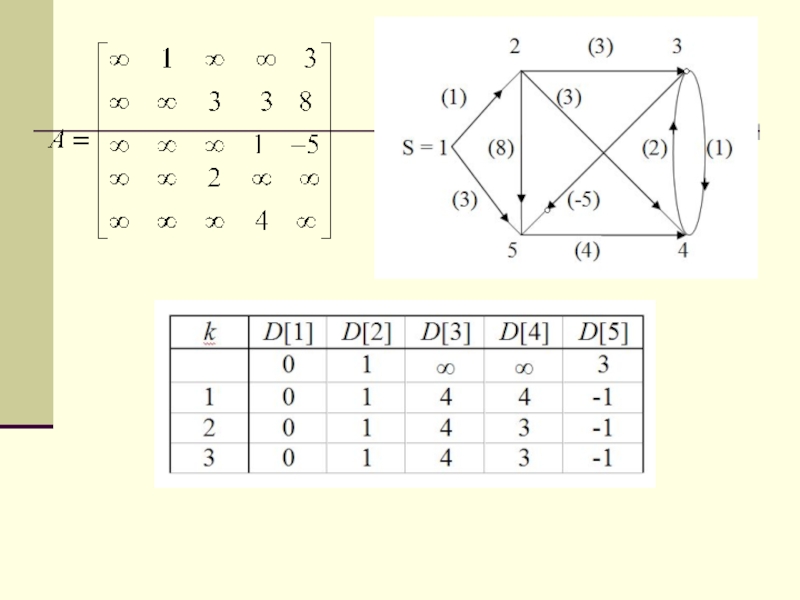
Слайд 8Пример: поиск кратчайшего пути
по известному кратчайшему расстоянию
Известно: d[2]=1, d[3]=4, d[4]=3,
d[5]=-1
Восстановим путь до вершины 5
Найдется вершина u, для которой
D[5] = D[u] + A[u,
5] очевидно u – вершина 3
-1 =4 -5
Найдется вершина u, для которой
D[3] = D[u] + A[u, 3] очевидно u – вершина 2
4 =1 +3
Найдется вершина u, для которой
D[2] = D[u] + A[u, 2] очевидно u – вершина 1
1 =0 +1
Итак, путь восстановлен
1-2-3-5
Слайд 9Сложность этого алгоритма
Пусть V, E —ориентированный граф, V = n, E = m. Если выбор
вершины u происходит в результате просмотра всех вершин, то сложность
нашего алгоритма — O(n2). Если мы просматриваем только список ПРЕДШ[v], содержащий все вершины u, такие что u v, то в этом случае сложность будет O(m).
Для неориентированного графа в случае положительных весов заменяем каждое ребро парой дуг!!!
Слайд 10Кратчайшие пути от фиксированной вершины
При данной матрице весов дуг A[u,
v], u, v V, вычисляются некоторые верхние ограничения D[v]
на расстояния от s до всех вершин v V. Каждый раз, когда мы устанавливаем, что D[u] + A[u, v] < D[v], оценку D[v] улучшаем: D[v] = D[u] + A[u, v].
Процесс прерывается, когда дальнейшее улучшение ни одного из ограничений невозможно.
Слайд 11Не известен ни один алгоритм нахождения расстояния между двумя фиксированными
вершинами, который был бы существенным образом более эффективным, нежели известные
алгоритмы определения расстояния от фиксированной вершины до всех остальных.
Слайд 12Алгоритм нахождения расстояния от источника до всех вершин —
метод
Форда — Беллмана
Данные: Ориентированный граф V, E с n вершинами с
выделенным источником s V, матрица дуг A[u, v], u, v V (граф не содержит контуров отрицательной длины).
Результаты: Расстояния от источника до всех вершин графа: D[v]=d(s, v), vV.
1 begin
2 for v V do D [v] := A[s, v]; D [s] := 0;
3 for k := 1 to n – 2 do
4 for v V \ {s} do
5 for u V do D [v] := min(D[v], D[u] + A [u, v])
6 end
Слайд 13Очевидно, что временная сложность алгоритма есть O(n3). Мы можем, конечно,
закончить вычисления, когда выполнение цикла 4 не вызывает изменения ни
одной из переменных D[v], v V. Это может наступить для k < n – 2, однако такая модификация алгоритма не изменяет существенным образом его сложности. Для редких графов (m << n2) удобнее представлять граф списками антецидентности ПРЕДШ[v], v V. Заменяя строку 5 на
for u ПРЕДШ[v] do D [v] := min(D[v], D[u] + A [u, v]),
получаем алгоритм со сложностью O(nm).
Слайд 15Случай неотрицательных весов — алгоритм Дейкстры
Пусть (V,E) — нагруженный граф,
и s — его вершина.
Алгоритм выбирает кратчайший путь от вершины
s до любой вершины v и присваивает его длину переменной d[v].
В списке PathTo(v) перечисляются вершины кратчайшего пути от s к v.
Слайд 16Begin
For каждой do
Begin
d[v] :=A(s, v)
PathTo(v):=s
end
Отметить
вершину s;
While есть неотмеченные вершины do
Begin
u:=неотмеченную вершину с мин. расст. от s;
отметить вершину u;
for каждой неотмеченной вершины v с условием uv E do
begin
d’ := d[u] + A(u, v) ;
If d’ < d[v] then begin
d[v] := d’ ; PathTo(v):=PathTo(u), v;
end;
end
End;
End
Слайд 19Пути в бесконтурном графе
Второй случай, для которого известен алгоритм нахождения
расстояний от фиксированной вершины за время O(n2) — случай, когда
граф является бесконтурным (веса дуг могут быть произвольными). Сначала докажем следующую лемму.
Лемма. В произвольном бесконтурном графе вершины можно перенумеровать так, что каждая дуга будет иметь вид vi, vj, где i < j.
Слайд 20Система ПЕРТ
Бесконтурные орграфы полезны в качестве моделей ситуаций, задачи
в которых должны выполняться в определенном порядке (контур в такой
интерпретации означает, что та или иная задача выполняется с некоторой периодичностью и должна предшествовать сама себе). В задаче о планировании заданий соответствующий бесконтурный граф имеет кодовое название «система ПЕРТ».
ПЕРТ — система планирования и руководства разработками. PERT — Program Evaluation and Review Technigue
Предположим, что необходимо определить порядок, в котором следует изучать предметы, учитывая их зависимость друг от друга. Это позволяет сделать алгоритм топологической сортировки. Алгоритм создает последовательность согласованных меток для вершин бесконтурного графа таким образом, что если 1, 2, 3, … — метки вершин и uv — дуга орграфа, идущая от вершины u с меткой i к вершине v с пометкой j, то .
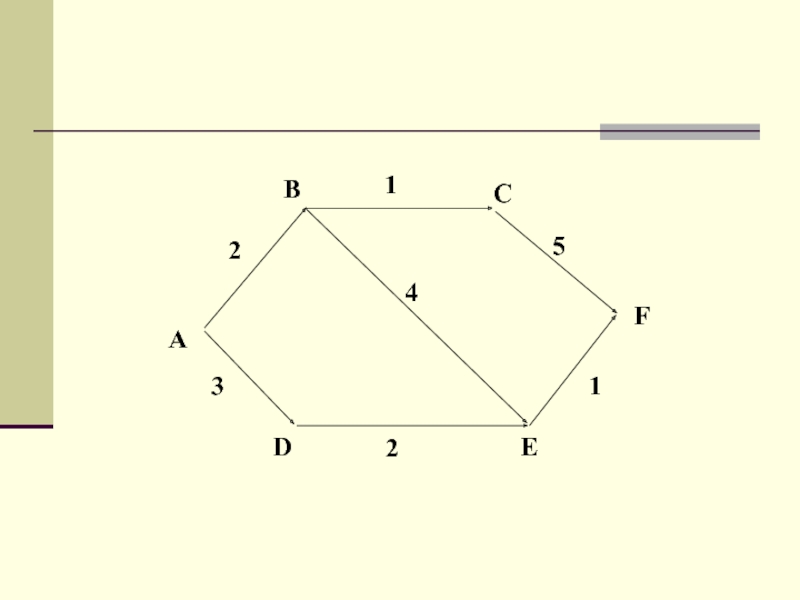
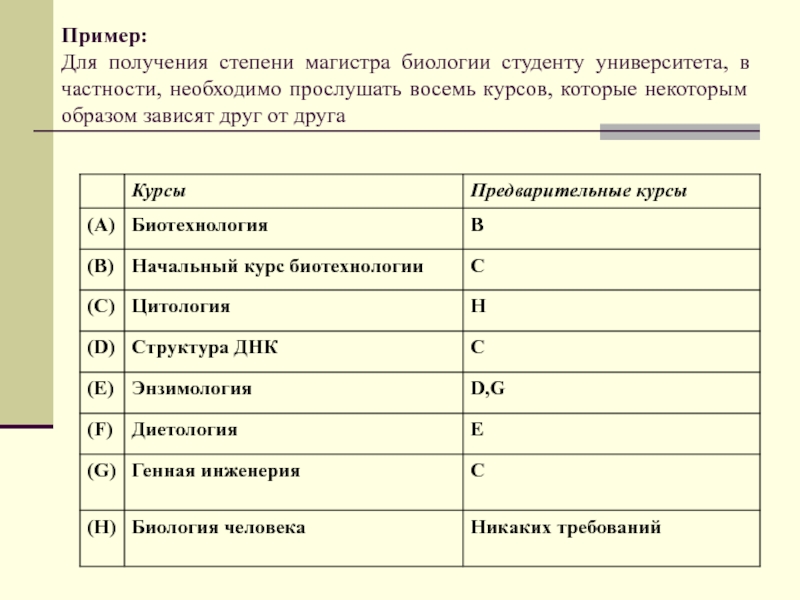
Слайд 21Пример:
Для получения степени магистра биологии студенту университета, в частности,
необходимо прослушать восемь курсов, которые некоторым образом зависят друг от
друга
Слайд 22Алгоритм нумерации вершин бесконтурного графа (топологической сортировки)
Данные: Ориентированный бесконтурный граф
V, E, определяемый списками инцидентности ЗАПИСЬ [v], v V.
Результаты: Для
каждой вершины v V номер NR[v], такой что для произвольной дуги u, v E выполняется неравенство NR[u] < NR[v].
Слайд 231 begin
2 for v V do
ЧЗАХ [v] := 0;
{ ЧЗАХ
[v] = число дуг, заходящих в v }
3 for u V do
4 for v ЗАПИСЬ [u] do ЧЗАХ [v] := ЧЗАХ [v] + 1;
5 СТЕК := ;
6 for v V do
7 if ЧЗАХ [v] = 0 then СТЕК v;
8 num := 0;
9 while СТЕК do
10 begin u СТЕК;
11 num := num + 1; NR[u] := num;
12 for v ЗАПИСЬ [u] do
13 begin ЧЗАХ [v] := ЧЗАХ [v] – 1;
14 if ЧЗАХ [v] = 0 then СТЕК v;
15 end
16 end
17 end
Слайд 24Алгоритм основывается на следующем простом факте: в произвольном (непустом) бесконтурном
графе существует вершина, в которую не заходит ни одна дуга.
В нашем алгоритме вершины, в которые не заходит ни одна дуга, накапливаются в стеке. В строке 10 выбирается верхний элемент стека u (это мог бы быть произвольный элемент стека), и этой вершине присваивается самый маленький из еще неиспользованных номеров. Таким образом, мы гарантируем то, что все дуги, выходящие из этой вершины, ведут к вершине с большими номерами. Затем вершина u вместе с выходящими из нее дугами удаляется из графа. Это приводит к уменьшению на единицу числа дуг, заходящих в каждую вершину v, такую что u v ; это число запоминается в ЧЗАХ [v]. Если для какой-нибудь из вершин v это число сводится к нулю, то v помещается в стек.
В силу бесконтурности графа и наших предыдущих замечаний полное опустошение стека, вызывающее окончание выполнения алгоритма (см. цикл 9), наступает не раньше, чем после присвоения номеров всем вершинам графа.
Легко заметить, что каждая дуга анализируется алгоритмом один раз в строке 4 и один раз в строке 12. Таким образом, сложность алгоритма есть O(m) (остается в силе предположение m = (n), в противном случае следовало бы написать O(m + n)).

Слайд 25Алгоритм нахождения расстояний от источника до всех вершин в бесконтурном
графе
Согласно вышеизложенному алгоритму при описании алгоритма нахождения путей в бесконтурном
графе мы можем предположить, что каждая дуга идет из вершины с меньшим номером в вершину с большим номером.
Данные: Ориентированный граф V, E, где V = {v1, ... , vn}, и для произвольной дуги vi, vj E имеем i < j. Этот граф определен списками антецедентности ПРЕДШ[v], v V.
Результаты: Расстояния от v1 до всех вершин графа:
D[vi] = d(v1, vi), i = 1, ..., n.
Слайд 261 begin
2 D[v1] := 0;
3 for j := 2 to
n do D[vj] := ;
4 for j := 2 to n do
5 for vi ПРЕДШ [vj] do D[vj] :=
min(D[vj]), D[vi] + A[vi, vj])
6 end
Слайд 27Сложность алгоритма порядка O(m), так как каждая дуга vi, vj анализируется
а строке 5 в точности один раз.
Описанные алгоритмы находят применения
в методах PERT (Project Evaluation and Review Technique) или CPM (Critical Path Method). Эти методы основываются на построении графа (сети PERT или сети CPM), дуги которого соответствуют некоторым элементарным задачам, составляющим проект, а их веса указывают на время, необходимое для решения отдельных задач.
Кроме этого, мы предполагаем, что для произвольных дуг этого графа u, v и v, t задача, изображаемая дугой u, v, должна быть закончена перед началом решения задачи, изображаемой дугой v, t.
Легко заметить, что такой граф должен быть бесконтурным. Нашей задачей является нахождение самого длинного пути из вершины s, соответствующей началу проекта, до вершины t, соответствующей его окончанию. Такой путь называется критическим путем. Его длина определяет время, необходимое для реализации всего проекта. Очевидно, что задача сводится к задаче о кратчайшем пути путем изменения знака каждого веса a(u, v), где u v, на обратный.

Слайд 28Кратчайшие пути между всеми парами вершин
Очевидно, что задачу определения расстояния
между всеми парами вершин можно решить, используя n раз один
из ранее изложенных методов нахождения расстояний от фиксированной вершины. Таким образом, мы получаем алгоритм со сложностью O(n4) (при использовании метода Форда — Беллмана) или O(n3) для бесконтурных графов или неотрицательных весов. Однако оказывается, что в общем случае n–кратное использование метода Форда — Беллмана не является наилучшим методом.
Слайд 29Улучшение. Способ 1
Рассмотрим ориентированный граф G = V, E, где V = {v1, ..., vn},
и предположим, что A = [aij] есть матрица весов (aij = a(vi, vj)). Обозначив через
dij(m) длину кратчайшего пути из vi в vj, содержащего не более m дуг, получаем следующие уравнения:
Слайд 30Если операцию min трактовать как «сумму», операцию «+» — как
«произведение», то матрица [dij(m+1)] является «произведением» матриц [dij(m)] и A = [aij].
Обозначим такое «произведение» двух матриц A и B через A*B. Для этой операции единичным элементом служит матрица
Слайд 32Произведение A*B двух матриц размерности n n можно вычислить за
время O(n3) (n сложений и n – 1 сравнений на
каждый из n2 элементов произведения A*B). Следовательно, матрицу и тем самым расстояние между всеми парами вершин можно вычислить за время O(n4) (как и для случая n–кратного использования алгоритма Форда — Беллмана).
Однако!!! заметим, что операция * ассоциативна (т.е. (A*B)*C = A*(B*C)). Этот факт позволяет вычислять произведение, поочередно возводя матрицу A в квадрат и тем самым заменяя n – 1 умножение матрицы log n умножениями. Таким образом, мы получаем алгоритм сложности O(n3log n), отыскивающий расстояния между всеми парами вершин в графе без контуров отрицательной длины.
Слайд 33Способ 2. Алгоритм Уоршалла и Флойда.
Обозначим через dij(m) длину кратчайшего
из путей из vi в vj с промежуточными вершинами в
множестве {v1, ..., vm}.
Тогда имеем следующие уравнения:
Обоснование второго уравнения достаточно простое. Рассмотрим кратчайший путь из vi в vj с промежуточными вершинами из множества {v1, ..., vm, vm+1}. Если этот путь не содержит vm+1, то
Если же он содержит vm+1, то деля путь на отрезки от vi до vm+1 и от vm+1 до vj, получаем равенство
Слайд 34Кратчайшие пути между всеми парами вершин
Данные: Матрица весов дуг
A[i, j], 1 i, j n, ориентированного графа без контуров отрицательной
длины.
Результаты: Расстояния между всеми парами вершин D[i, j] = d(vi, vj).
1 begin
2 for i := 1 to n do
3 for j := 1 to n do D[i, j] := A[i, j];
4 for i := 1 to n do D[i, i] := 0;
5 for m := 1 to n do
6 for i := 1 to n do
7 for j := 1 to n do
8 D[i, j] := min(D[i, j], D[i, m] + D[m, j];
9 end
Слайд 35Очевидно, что сложность этого алгоритма есть O(n3). !!! Такую же
сложность имел алгоритм Форда —Беллмана нахождения расстояний от фиксированной вершины
до всех остальных вершин. Любопытно, что для общего случая (т.е. без предположения о неотрицательности весов либо о бесконтурности графа) не известен ни один алгоритм нахождения расстояния между одной фиксированной парой вершин, который был бы значительно эффективнее алгоритма нахождения расстояний между всеми парами вершин.
Слайд 36С задачей определения кратчайших путей в графе тесно связана задача
транзитивного замыкания бинарного отношения. Отношение является транзитивным, если выполняется условие
если x, y E и y, z E , то x, z E
для произвольных x, y, z E.
Заметим, что бинарное отношение E VV можно однозначно представить ориентированным графом G = V, E. Для произвольного такого отношения мы определяем E* = { x, y: в V, E существует путь ненулевой длины из x в y}.
Нетрудно заметить, что E* — транзитивное отношение на множестве V и E E*. Более того, E* является наименьшим транзитивным отношением, содержащим E, т.е. для произвольного транзитивного отношения F E выполняется включение E* F. Отношение E* называется транзитивным замыканием отношения E.
Слайд 37Если отношение E представить в виде графа V, E, в котором
каждая дуга имеет вес 1, то транзитивное замыкание E* можно
вычислить с помощью алгоритма Флойда за время O(n3); после завершения работы имеем
vi, vj E* D[i, j] < .
При вычислении транзитивного замыкания удобно принять
Слайд 38Тогда строку 8 в алгоритме можно заменить на
D[i, j] := D[i, j] (D[i, m]
D[m, j] ),
где и — обычные булевы операции.
После
завершения работы алгоритма, модифицированного таким образом (принадлежащего Уоршаллу), очевидно, имеем
Слайд 39Известен алгоритм построения транзитивного замыкания, более эффективный, чем алгоритм Уоршалла.
Он использует связь этой задачи с умножением матриц. Эта связь
для матриц A приводит к обычному умножению булевых матриц по формуле
Слайд 40Такое умножение можно выполнить за время O(nlog 7), что дает алгоритм
построения транзитивного замыкания, имеющего сложность O(nlog 7 log n). Такой алгоритм имеет скорее
теоретическое значение, поскольку метод умножения матриц за время O(nlog 7) является довольно сложным и, следовательно, обнаруживает свое преимущество перед обычным «школьным» методом только при очень больших значениях n. На практике обычно самым эффективным оказывается алгоритм Уоршалла, соответствующим образом запрограммированный.
Слайд 41Другим способом построения транзитивного замыкания отношения E является применение поиска
в глубину (или в ширину) в графе V, E. Этот способ
особенно выгоден, когда отношение E симметрично; очевидно, что тогда транзитивное замыкание строится отдельно для каждой связной компоненты, на которые разбивается неориентированный граф, определяемый отношением E, и это построение может быть получено за время O(m + n).
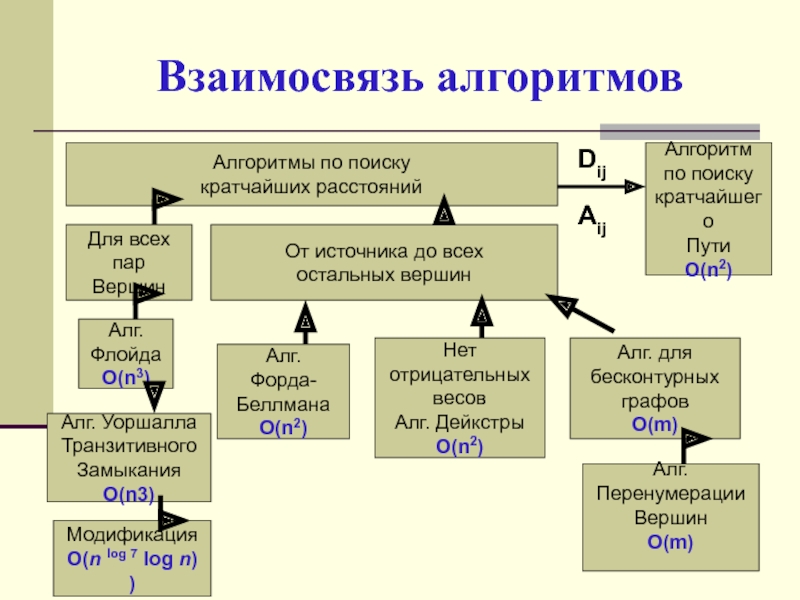
Слайд 42Взаимосвязь алгоритмов
Алгоритмы по поиску
кратчайших расстояний
Алгоритм
по поиску
кратчайшего
Пути
О(n2)
Dij
Aij
Для всех
пар
Вершин
Алг.
Форда-
Беллмана
O(n2)
От источника до всех
остальных вершин
Алг.
Флойда
O(n3)
Нет
отрицательных
весов
Алг. Дейкстры
O(n2)
Алг. для
бесконтурных
графов
О(m)
Алг.
Перенумерации
Вершин
О(m)
Алг. Уоршалла
Транзитивного
Замыкания
O(n3)
Модификация
O(n log 7 log n) )






![НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ Нахождение кратчайшего пути между фиксированными вершинами s, t VДанные: Расстояния Нахождение кратчайшего пути между фиксированными вершинами s, t VДанные: Расстояния D[v] от фиксированной вершины s до](/img/tmb/3/294301/5ef20882469f3693da89eeb96ea46c52-800x.jpg)
![НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ Пример: поиск кратчайшего пути по известному кратчайшему расстояниюИзвестно: d[2]=1, d[3]=4, d[4]=3, Пример: поиск кратчайшего пути по известному кратчайшему расстояниюИзвестно: d[2]=1, d[3]=4, d[4]=3, d[5]=-1Восстановим путь до вершины 5Найдется вершина](/img/tmb/3/294301/9ea63b4973dd791b86318e9a7a9121e3-800x.jpg)

![НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ Кратчайшие пути от фиксированной вершиныПри данной матрице весов дуг A[u, v], Кратчайшие пути от фиксированной вершиныПри данной матрице весов дуг A[u, v], u, v V, вычисляются некоторые](/img/thumbs/2b00cfd66fc63b7753c3c3d1b5196f01-800x.jpg)




![НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ Begin For каждой do Begin d[v] :=A(s, v) Begin For каждой do Begin d[v] :=A(s, v)](/img/thumbs/d14a19de1aa89bdcb14b7f6e79de4a1a-800x.jpg)



![НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ Алгоритм нумерации вершин бесконтурного графа (топологической сортировки) Данные: Ориентированный бесконтурный граф Алгоритм нумерации вершин бесконтурного графа (топологической сортировки) Данные: Ориентированный бесконтурный граф V, E, определяемый списками инцидентности ЗАПИСЬ [v],](/img/thumbs/883e807cdc9502084bca5ccd79c09d80-800x.jpg)
![НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ 1 begin2 for v V do ЧЗАХ [v] := 0; 1 begin2 for v V do ЧЗАХ [v] := 0;](/img/thumbs/b8c113e9a8c60b9b034f22f735417081-800x.jpg)


![НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ 1 begin2 D[v1] := 0;3 for j := 2 to n do D[vj] := ;4 1 begin2 D[v1] := 0;3 for j := 2 to n do D[vj] := ;4 for j := 2](/img/thumbs/1861cc83873ca40f28bfd284df8ca873-800x.jpg)


![НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ Улучшение. Способ 1Рассмотрим ориентированный граф G = V, E, где V = {v1, ..., vn}, и Улучшение. Способ 1Рассмотрим ориентированный граф G = V, E, где V = {v1, ..., vn}, и предположим, что A = [aij] есть матрица весов](/img/thumbs/2008be6d60f9263b372d928cc1daf173-800x.jpg)
![НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ Если операцию min трактовать как «сумму», операцию «+» — как «произведение», Если операцию min трактовать как «сумму», операцию «+» — как «произведение», то матрица [dij(m+1)] является «произведением» матриц](/img/thumbs/109eaf2ba230bdfd54de0b695dcfa79c-800x.jpg)
![НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ Тогда [dij(0)] = U и Тогда [dij(0)] = U и](/img/tmb/3/294301/0dc0348905ef44fd7d315d0ff956c6c0-800x.jpg)


![НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ Кратчайшие пути между всеми парами вершин Данные: Матрица весов дуг A[i, j], Кратчайшие пути между всеми парами вершин Данные: Матрица весов дуг A[i, j], 1 i, j n, ориентированного графа](/img/thumbs/53fc8374cdef02310881f3d30d4faeef-800x.jpg)



![НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ Тогда строку 8 в алгоритме можно заменить наD[i, j] := D[i, j] (D[i, m] D[m, j] ),где Тогда строку 8 в алгоритме можно заменить наD[i, j] := D[i, j] (D[i, m] D[m, j] ),где и — обычные булевы](/img/thumbs/f23ae2667c7034c68e43cd7a45127904-800x.jpg)