Національний університет "Львівська політехніка" Фінансовий

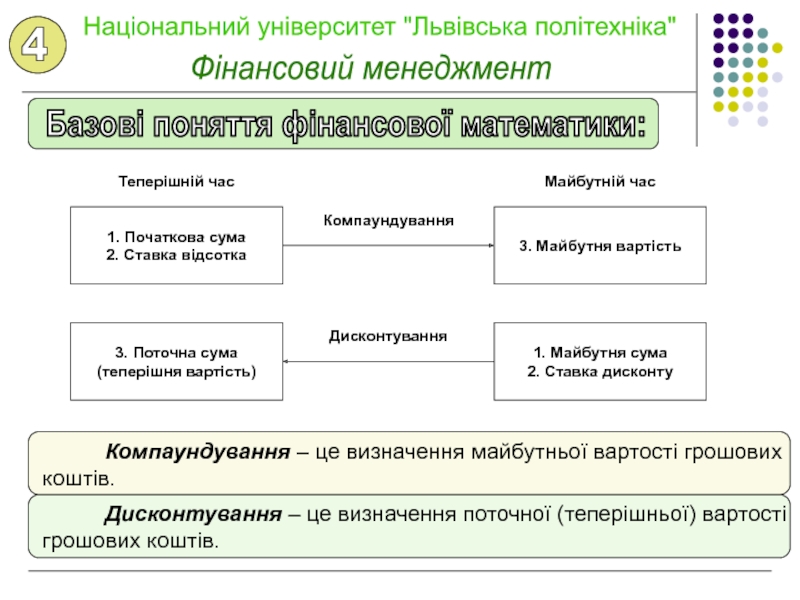
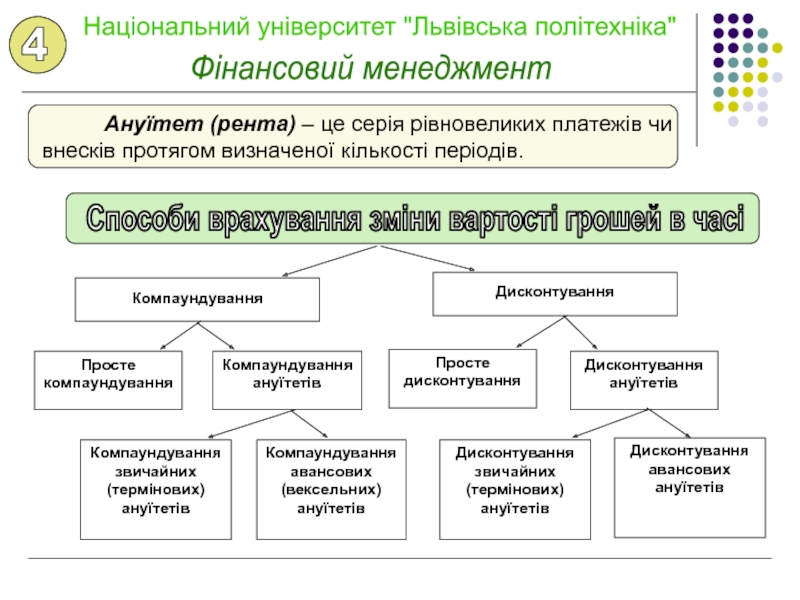
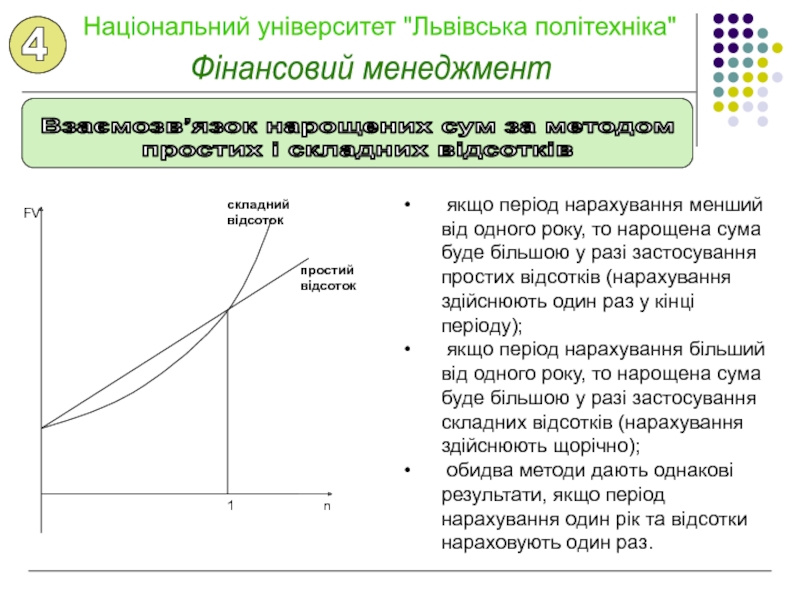
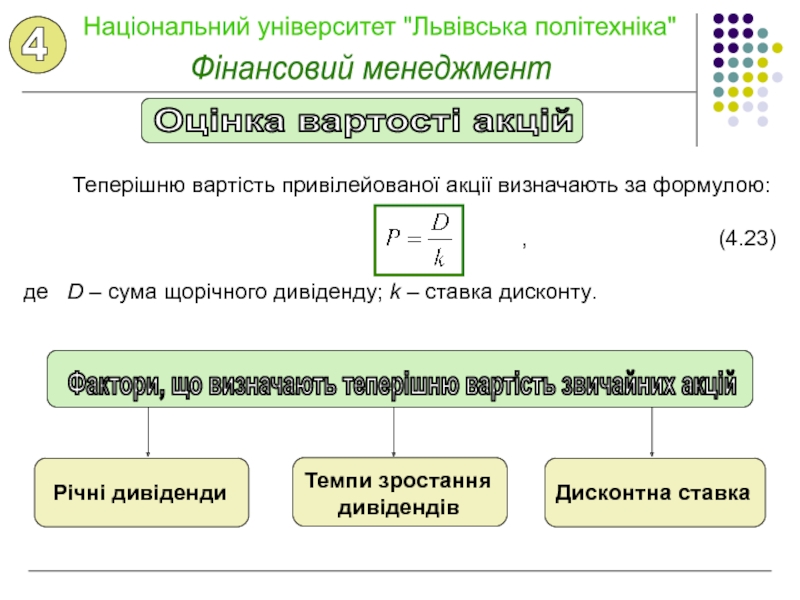
грошей з часом змінюється з урахуванням норми прибутку на фінансовому

ринку. Як норму прибутку переважно вибирають ставку позикового відсотка.
Отже, згідно з цією концепцією, одна грошова одиниця сьогодні має більшу вартість, ніж в будь-якому майбутньому періоді.

необхідно років, щоб при встановленому відсотку сума капіталу подвоїлася. Наприклад,

за відсотка 9 для подвоєння капіталу необхідно 8 років (72 / 9 = 8 років).

= PV · n · i ,

(4.1)
де PV – початкова сума грошових коштів (теперішня вартість);
n – кількість інтервалів, за якими здійснюється розрахунок відсоткових платежів за обумовлений період;
і – відсоткова ставка.


Майбутня вартість вкладених сьогодні грошових коштів визначається за формулою:
FV = PV + I = PV · ( 1 + n · i ) , (4.2)
де (1 + n × i ) – коефіцієнт нарощення суми простих процентів.

(n

якими здійснюють розрахунок відсоткових платежів; К – кількість днів у році.

Можливі такі варіанти обчислень:
звичайні відсотки: t – наближене, K = 360 днів. Такий підхід ще називають німецьким методом нарахування відсотків;
комерційні відсотки: t – точне, K = 360 днів. Його називають банківським або французьким;
точні відсотки: t – точне, K = 365 днів або K = 366 днів. Цей метод ще називають англійським.

обчислюють за формулою:

,

(4.4)

де n – кількість років накопичення.

З огляду на це сума відсотків дорівнює:

(4.5)

Майбутню вартість коштів FV у разі нарахування складних відсотків m разів за рік протягом n років обчислюють за формулою:
(4.6)

сума буде більшою у разі застосування простих відсотків (нарахування здійснюють

один раз у кінці періоду);
якщо період нарахування більший від одного року, то нарощена сума буде більшою у разі застосування складних відсотків (нарахування здійснюють щорічно);
обидва методи дають однакові результати, якщо період нарахування один рік та відсотки нараховують один раз.

(4.7)

б) пренумерандо:

, (4.8)

де PMT – абсолютна величина періодичних рівновеликих виплат (ануїтетів).

) складають рівняння еквівалентності:

(4.10)

визначається приведенням – дисконтування на величину (суму) відсотка, який міг

би бути заробленим, якщо б грошові кошти були доступні для їх використання на момент оцінювання.
Застосовують такі моделі дисконтування:
просте дисконтування;
дисконтування ануїтетів (теперішньої або авансової ренти).

Дисконтування майбутніх грошових потоків здійснюють використанням:
а) простого відсотка:
(4.11)
б) складного відсотка
(4.12)

визначити за формулами:
при звичайному (терміновому) ануїтеті (постнумерандо):

,

(4.13)

де PMT – абсолютна величина періодичних виплат за ануїтетом.
– дисконтний множник ануїтету

при авансовому (вексельному) ануїтеті (пренумерандо).
(4.14)
Теперішню вартість довічної ренти визначають за формулою:

(4.15)

(4.16)
де Sінф

– номінальна майбутня вартість грошових коштів, яка враховує фактор інфляції;
Р – початкова сума вкладу;
іp – реальна відсоткова ставка, виражена десятковим дробом;
α – прогнозований темп інфляції, виражений десятковим дробом;
n – кількість інтервалів, за які здійснюють кожний відсотковий платіж, в загальному періоді часу.

, (4.17)

де ін – номінальна (фактична) відсоткова ставка.

(4.18)
де Sл – майбутня вартість грошових коштів, яка враховує фактор ліквідності;
іл – середня річна норма дохідності за інвестиційними проектами (інструментами) з абсолютною ліквідністю, виражена десятковим дробом;
rл – необхідний рівень премії за ліквідність, виражений десятковим дробом.

, (4.19)
де ЗПл — загальний період ліквідності конкретного об’єкту інвестування.

(4.20)
де Sр – майбутня вартість з урахуванням фактора ризику;
іб – безризикова норма дохідності на фінансовому ринку, виражена десятковим дробом;
rр – рівень премії за ризик для конкретного фінансового інструменту (фінансовій операції), виражений десятковим дробом.

, (4.21)
де — середня норма дохідності на фінансовому ринку, %;
іб — безризикова норма дохідності на фінансовому ринку, %;
β — бета-коефіцієнт, що характеризує рівень систематичного ризику для конкретного фінансового (фондового) інструмента

(4.22)

де – сума отриманих відсотків (купонного доходу) в кожному і-му періоді, який обчислюють як добуток номінальної вартості облігації на оголошену купонну ставку відсотка;
Но – номінальна вартість облігації;
е – дисконтна ставка;
n – термін погашення облігації.

формулою:

,

(4.23)

де D – сума щорічного дивіденду; k – ставка дисконту.

оцінки вартості акцій з постійними дивідендами застосовують формулу:
,

(4.24)
де Ра — реальна вартість акцій зі стабільним рівнем дивідендів; D – річна сума постійного дивіденду; Ks – необхідна ставка доходу звичайних акцій, виражена десятковим дробом.

Для оцінки акцій з постійним приростом дивідендів застосовують формули, запропоновані Майроном Дж. Гордоном:

або
(4.25)
де Р0 —реальна вартість акції з постійно зростаючим рівнем дивідендів;D0 – сума останнього сплаченого дивіденду на акцію; D1 – сума очікуваного дивіденду на акцію через рік; d – темп приросту дивідендів, виражений десятковим дробом; КS – необхідна ставка доходу на акції, виражена десятковим дробом.

оцінки вартості акцій з плаваючим приростом дивідендів слід обчислити майбутні

дивіденди окремо за кожен період, потім дисконтувати ці суми до теперішньої вартості і підсумувати отримані результати:

, (4.31)


Необхідну ставку доходу на акції визначають за формулою:

, (4.32)
де Rf – безпечна ставка доходу (дохідність державних облігацій), %;
Rm – ринкова ставка доходу, %;
β – бета-коефіцієнт підприємства.