Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нелинейная оптимизация. Метод Нелдера-Мида
Содержание
- 1. Нелинейная оптимизация. Метод Нелдера-Мида
- 2. В презентацииМинимизацияМетоды нулевого порядкаМетод Нелдера-МидаАлгоритмОбласти применения Программа на паскале Обзор Сходимость Приложения Заключение Рекомендации
- 3. Цель проекта Разработка и внедрение программы минимизации функцийПриемы программирования
- 4. Историческая справкаJEFFREY C. LAGARIAS, JAMES A. REEDS,
- 5. Метод впервые был опубликован в работеJ. A.
- 6. Историческая справкаМетод активно используется при решении прикладных
- 7. Алгоритм Нелдера-МидаАлгоритм Нелдера-Мида минимизирует скалярную нелинейную функцию
- 8. Алгоритм Нелдера-МидаОбычно метод, базирующийся на итерациях на
- 9. Алгоритм Нелдера-МидаИтак, метод Нелдера-Мида минимизации функции определяется
- 10. Одна итерация метода1. Упорядочивание. Сортировка n +
- 11. Одна итерация метода3. Растяжение. Если
- 12. 4. Сжатие. Если
- 13. Одна итерация метода4. Сжатие. Внутреннее. Если
- 14. Одна итерация метода5. Глобальное сжатие. Вычисляем значения
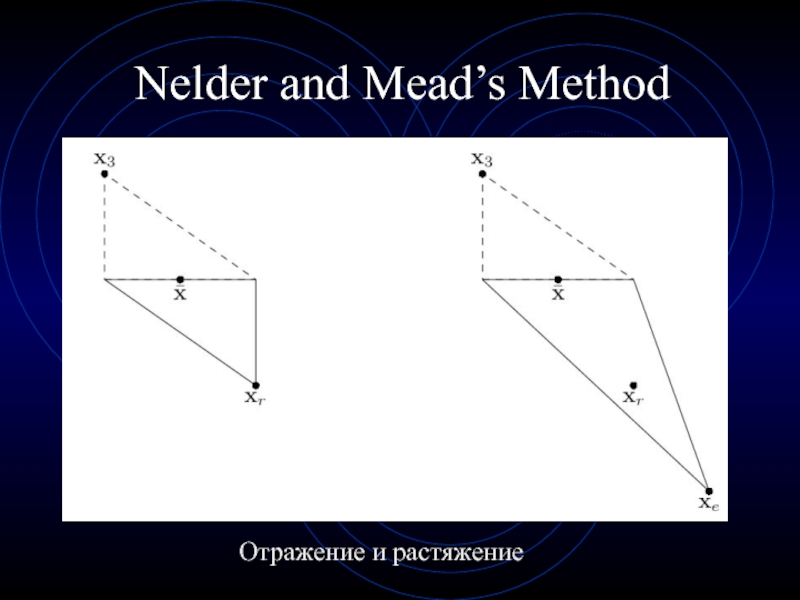
- 15. Nelder and Mead’s MethodОтражение и растяжение
- 16. Nelder and Mead’s MethodВнешнее, внутреннее и глобальное сжатие
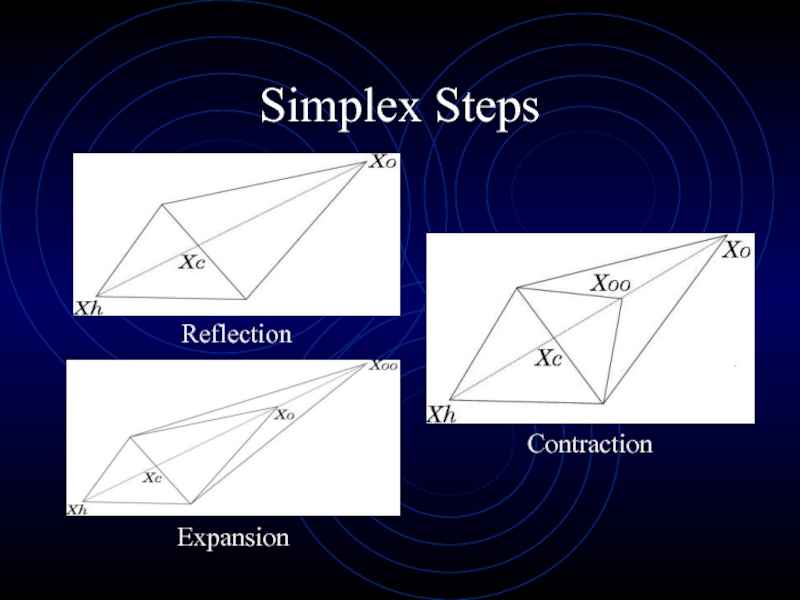
- 17. Simplex StepsReflectionExpansionContraction
- 18. Limitations An interesting open problem concerns whether
- 19. Applicationsfunction Func(X : TeVector) : Extended;begin result
- 20. function Simplexfunction Simplex(Func: TFuncNVar; X: TeVector; Lbound,
- 21. ConclusionsOur general conclusion about the Nelder{Mead algorithm
- 22. RecommendationsИспользуйте алгоритм Нелдера-Мида в случаях:Необходимо быстро написать
- 23. Questions?
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Нелинейная оптимизация.
Метод Нелдера-Мида
Константин Ловецкий
Кафедра телекоммуникаций
Сентябрь, 2012
Слайд 2В презентации
Минимизация
Методы нулевого порядка
Метод Нелдера-Мида
Алгоритм
Области применения
Программа на паскале
Обзор
Сходимость
Слайд 4Историческая справка
JEFFREY C. LAGARIAS, JAMES A. REEDS, MARGARET H. WRIGHT,
AND PAUL E. WRIGHT.
NELDER-MEAD SIMPLEX METHOD IN LOW DIMENSIONS
SIAM
J. OPTIM. °c 1998 Society for Industrial and Applied MathematicsVol. 9, No. 1, pp. 112-147
Симплекс-метод Нелдера-Мида, впервые опубликованный в 1965 году, неимоверно популярен в качестве метода прямого поиска решения в задачах многомерной оптимизации без ограничений. Однако, несмотря на широкое распространение метода, теоретические результаты о его сходимости практически отсутствуют.
Рассмотрим сходимость этого метода для строго выпуклых функций в пространствах размерности 1 и 2 по материалам статьи авторов, работающих в AT&T Labs-Research, Florham Park, NJ 07932 и Bell Laboratories, Murray Hill, NJ 07974
Докажем сходимость метода к минимуму в пространстве размерности 1 и несколько более слабых результатов о сходимости в пространстве размерности 2. Контрпример МакКиннона (McKinnon) показывает, что существует семейство строго выпуклых функций в пространстве размерности 2 и существуют множества начальных условий, при которых метод Нелдера-Мида не сходится к точке минимума. Поэтому остается открытым вопрос, можно ли доказать сходимость метода для некоторого специального, но достаточно широкого класса выпуклых функций даже в двухмерном пространстве.
Слайд 5Метод впервые был опубликован в работе
J. A. Nelder and R.
Mead, A simplex method for function minimization, Computer Journal 7
(1965), 308-313.Историческая справка
С момента первой публикации симплекс метод Нелдера и Мида стал одним из наиболее популярных методов решения задач многомерной минимизации без ограничений. Сам метод не надо путать с (возможно) более известным методом Данцига (Dantzig) решения задач линейного программирования; оба метода при решении задач используют последовательность симплексов, однако на этом их сходство заканчивается.
Метод Нелдера-Мида предназначен исключительно для решения задач минимизации без ограничений.
Слайд 6Историческая справка
Метод активно используется при решении прикладных оптимизационных задач в
таких областях, как инженерная химия и медицина.
Особую популярность метод
приобрел после появления его описания в известной книге Numerical Recipes, где он появился под названием «амеба-алгоритм» и в пакете Matlab.Слайд 7Алгоритм Нелдера-Мида
Алгоритм Нелдера-Мида минимизирует скалярную нелинейную функцию n действительных переменных
используя лишь вычисление значений функции и не используя информацию о
ее производных (явно либо неявно). Тем самым метод попадает в общий класс прямых методов поиска.Большой подкласс таких методов, включая и метод Нелдера-Мида, опирается на вычисление на каждом шаге невырожденного симплекса, геометрической фигуры ненулевого объема в n-мерном пространстве, являющейся выпуклой оболочкой n + 1 вершины.
Слайд 8Алгоритм Нелдера-Мида
Обычно метод, базирующийся на итерациях на основе симплекса, начинает
с определения самого симплекса и определения его (n+1)-ой вершины, а
также вычисления соответствующих этим вершинам значений функции.Затем вычисляются одна или несколько пробных вершин и значений функции в них. Переход к новой итерации осуществляется после замены одной из предыдущих вершин новой вершиной.
Итерации прекращаются по достижении заданной точности (определяется как по разности значений функции, так и по объему многогранника – симплекса).
Слайд 9Алгоритм Нелдера-Мида
Итак, метод Нелдера-Мида минимизации функции
определяется четырьмя скалярными параметрами:
коэффициентами
отражения ( ),
растяжения( ),
сжатия (
), и глобальное сжатие ( ) — гомотетия к точке с наименьшим значением.
В оригинальной работе авторов на эти параметры накладывались условия:
Обычно в стандартной реализации алгоритма выбирают
Слайд 10Одна итерация метода
1. Упорядочивание. Сортировка n + 1 вершины так,
что f(x1) ≤ f(x2) ≤… ≤ f(xn+1);
2. Отражение. Вычислить
точку отражения по формулегде - центр тяжести n лучших точек. Вычислить .
Если ,, то добавить в набор точку отражения и закончить итерацию.
Слайд 11Одна итерация метода
3. Растяжение. Если
, то вычисляем точку растяжения xe,
Вычисляем
. Если , то добавляем эту точку в набор и переходим к новой итерации. В противном случае ( ) добавляем в набор точку xr.
Итерация закончена.
Слайд 124. Сжатие. Если ,
то проводим операцию сжатия между и лучшей точкой из
и :Внешнее. Если , то есть существенно лучше , то проводим внешнее сжатие:
Вычисляем и добавляем в набор, если . Переходим к (п.5)
Одна итерация метода
Слайд 13Одна итерация метода
4. Сжатие.
Внутреннее. Если
, то проводим внутреннее сжатие:
Вычисляем
и добавляем точку в набор, если .Переходим к глобальному сжатию (п.5)Слайд 14Одна итерация метода
5. Глобальное сжатие.
Вычисляем значения функции f(x) в
n точках
Упорядочиваем их. Новыми вершинами являются точки
Слайд 18Limitations
An interesting open problem concerns whether there exists any
function f(x) in R2 for which the Nelder-Mead algorithm always
converges to a minimizer. The natural candidate is f(x; y) = x2 + y2, which by ane-invariance is equivalent to all strictly convex quadratic functions in two dimensions. A complete analysis of Nelder-Mead for x2 + y2 remains an open problem.Слайд 19Applications
function Func(X : TeVector) : Extended;
begin
result := sqr(x[1]-1)+sqr(x[2]-1)+sqr(x[3]-1);
end;
procedure TForm1.btCalculateClick(Sender:
TObject);
var
X : TeVector; MaxIter, Iter: integer; F_min
: extended;begin
setlength(x, 4);
MaxIter:= 1500; // максимальное число итераций
x[1] := -0.1; // начальное приближение
x[2] := 1.1;
x[3] := 2.1;
Simplex(Func, X, 1, 3, MaxIter, 1.e-14, F_min, Iter, 0.1, 1.0e-8, nil, 0, '');
Label1.Caption := floattostr(x[1])+'; '+floattostr(x[2])+'; '+floattostr(x[3]);
Label2.Caption := Inttostr(Iter)+'; ';
x := nil;
end;
Слайд 20function Simplex
function Simplex(Func: TFuncNVar; X: TeVector; Lbound, Ubound: Integer;
MaxIter: Integer; Tol:
Extended;var F_min: Extended; var Iter: Integer{Iteration count};
Step: Extended; {для задания начального многогранника: скорее процент от текущей координаты}
ZeroCoordinateValue: Extended; {ноль, при котором шаг следует брать специфическим}
SB: TStatusBar; PanelN: Integer; PrefixStr: string): Integer;
{ ----------------------------------------------------------------------
Minimization of a function of several variables by the simplex method
of Nelder and Mead
----------------------------------------------------------------------
Input parameters : Func = objective function
X = initial minimum coordinates
Lbound,
Ubound = indices of first and last variables
MaxIter = maximum number of iterations
Tol = required precision
Step = Step used to construct the initial simplex ~ 1.5
----------------------------------------------------------------------
Output parameters : X = refined minimum coordinates
F_min = function value at minimum
Possible results : OPT_OK
OPT_NON_CONV
---------------------------------------------------------------------- }
















![Нелинейная оптимизация. Метод Нелдера-Мида Applicationsfunction Func(X : TeVector) : Extended;begin result := sqr(x[1]-1)+sqr(x[2]-1)+sqr(x[3]-1);end;procedure TForm1.btCalculateClick(Sender: TObject);var Applicationsfunction Func(X : TeVector) : Extended;begin result := sqr(x[1]-1)+sqr(x[2]-1)+sqr(x[3]-1);end;procedure TForm1.btCalculateClick(Sender: TObject);var X : TeVector; MaxIter, Iter:](/img/thumbs/097f29d439877dd1b03bd645112ed9cd-800x.jpg)























