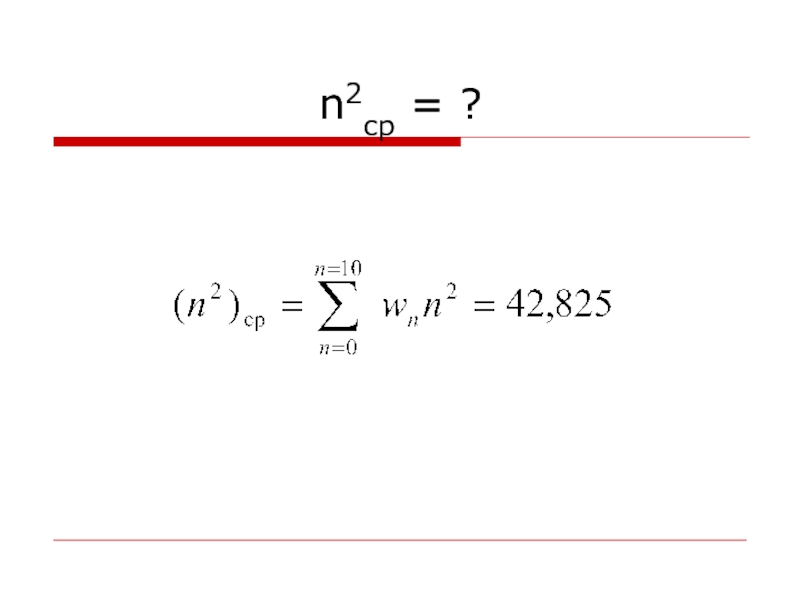Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Олимпиадный эксперимент – в школьный практикум
Содержание
- 1. Олимпиадный эксперимент – в школьный практикум
- 2. Все задачи в предлагаемой презентации - авторские
- 3. Полезные сайтыОлимпиадная школа МФТИ, курс «Экспериментальная физика»:
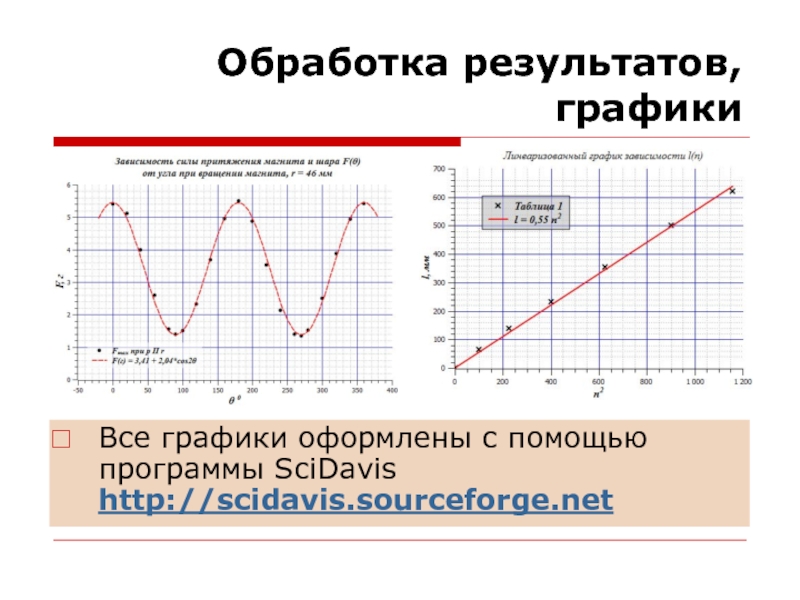
- 4. Обработка результатов, графикиВсе графики оформлены с помощью программы SciDavis http://scidavis.sourceforge.net
- 5. Наши планыIEPhO-4 (2016 г.)Неваляшка ЛестницаЛягушкаЗубочисткаСлинки (Slinky)IEPhO-3 (2015 г.)Удельное сопротивление воздуха Гук или не Гук
- 6. Неваляшка, IEPhO-4 (8, 9 классы)
- 7. ОборудованиеНеваляшкадеревянная линейка 50 см кусок пластилинакарандаш (ручка) лист бумаги
- 8. ЗаданиеС помощью имеющегося оборудования определите как можно
- 9. Решение. Шаг № 1По длине окружности C
- 10. Шаг № 2Подбираем кусок пластилина такой массы
- 11. Шаг № 3Уравновешиваем Неваляшку на «рычажных весах»,
- 12. Шаг № 4Отношение масс линейки и пластилина
- 13. Заключительный шаг (без картинки)Центр масс Неваляшки расположен
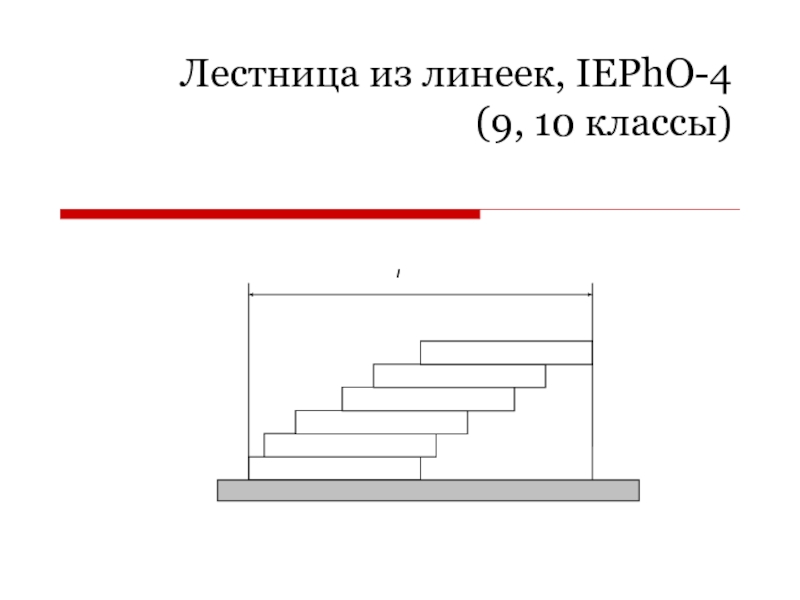
- 14. Лестница из линеек, IEPhO-4 (9, 10 классы)
- 15. Оборудование 11 деревянных линеек длиной ℓ0 = 21 см каждая, линейка 50 см
- 16. ЗаданиеПостройте ступенчатую лестницу максимальной (по горизонтали) длины
- 17. Строим лестницы
- 18. Теория: Δk = ℓ0/2k; ℓТ =
- 19. Наши линейкиΔ1=0,5ℓ0/1 = 105 ммΔ2=0,5ℓ0/2 = 52,5
- 20. 12 линеек, 240 линеекN = 12 ℓT(8)≈
- 21. Лягушка (8, 9 классы)Оборудование: кистевой эспандер
- 22. Решение: коэффициент трения полиэтилена μп Кладём «Лягушку»
- 23. Решение: коэффициент трения «лягушки» μл Переворачиваем «установку»
- 24. Определение числа π вероятностным методом (11 класс)Случайность – форма проявления закономерности
- 25. Задача Бюффона о бросании иглы (1777
- 26. Оборудование10 зубочисток лист бумаги с параллельными линиями. Расстояние между линиями равно длине зубочистки ℓ0
- 27. ЗаданиеЭкспериментально исследовать закон распределения w(n) случайной величины
- 28. Причём здесь π? (теория)Вероятность пересечь линию для
- 29. Как проводим опытОдновременно бросаем с высоты ~
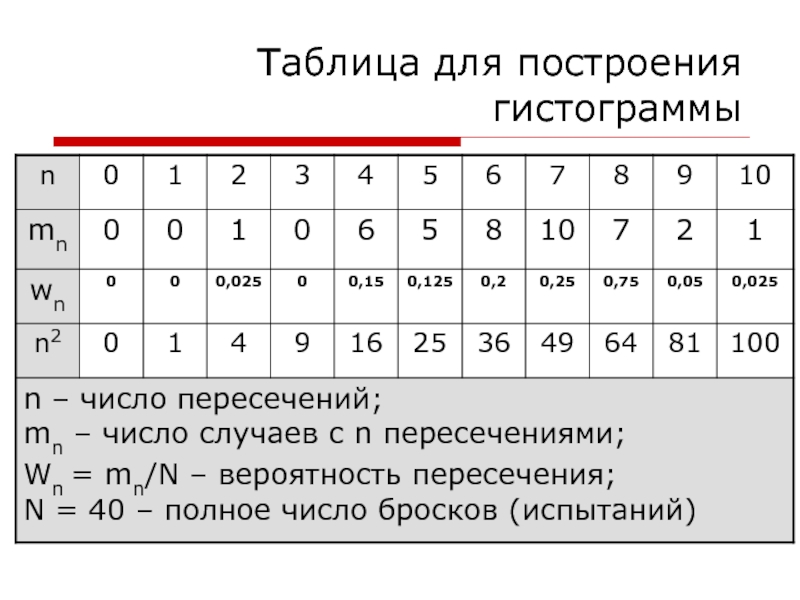
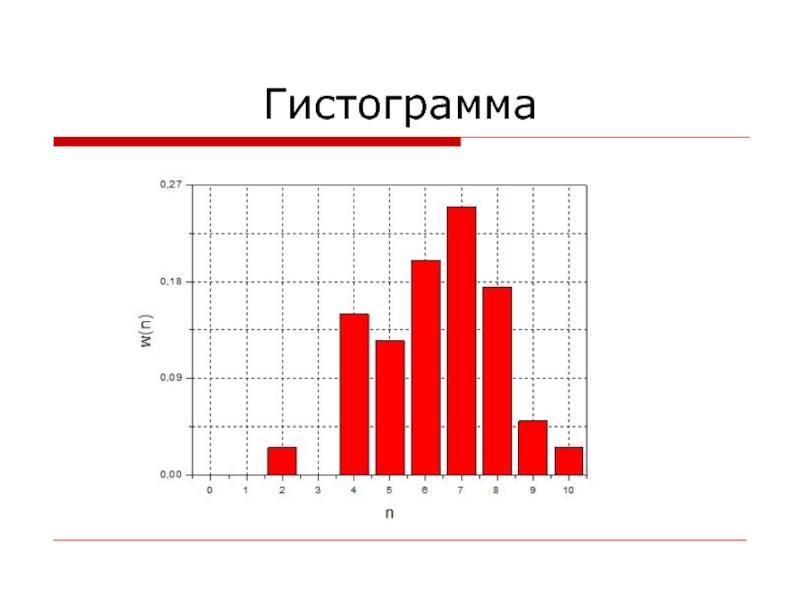
- 30. Таблица для построения гистограммы
- 31. Гистограмма
- 32. Считаем среднее nсрnср = ∑ni/N = ∑mnn/N = 6,325
- 33. Погрешность среднего σ
- 34. n2ср = ?
- 35. Результат: wтеор = 2/π π =
- 36. Изучение упругих свойств пластиковой пружины Слинки
- 37. Задание (статика)Снимите зависимость ℓ(n) длины ℓ
- 38. ℓ(n) - теорияПолучим теоретическую зависимость ℓ(n), выразив
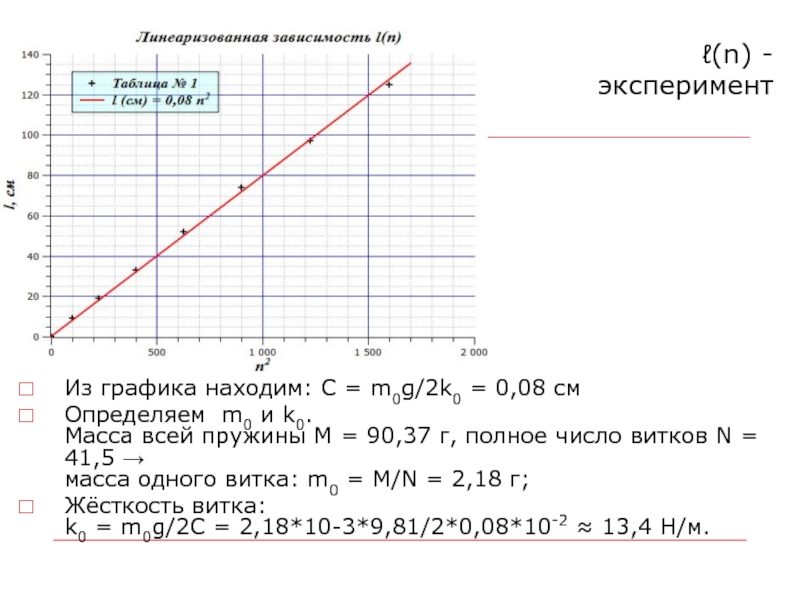
- 39. ℓ(n) - экспериментИз графика находим: C =
- 40. Задание (динамика)Снимите зависимость T(n) периода колебаний
- 41. T(n) - теорияT = 2π(βm/k)1/2 = 2π(βnm0/(k0/n))1/2
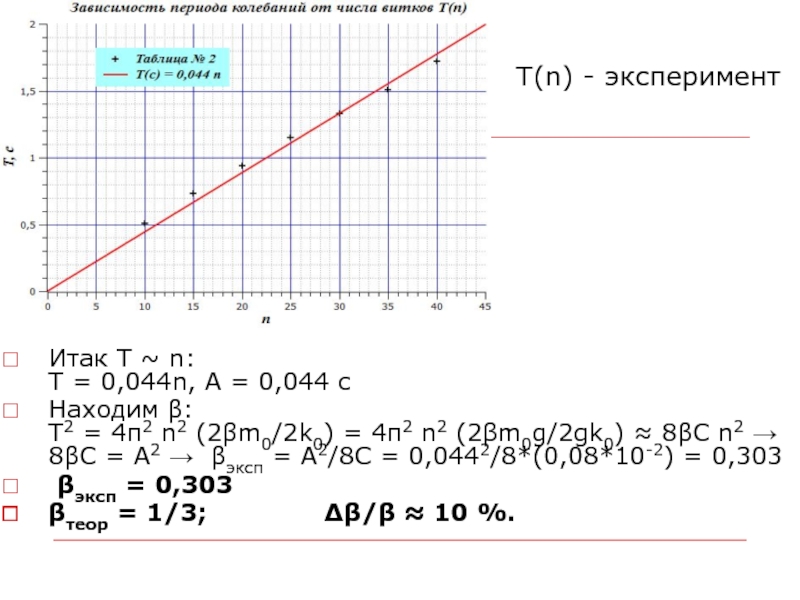
- 42. T(n) - экспериментИтак T ~ n: T
- 43. Удельное электросопротивление воздуха
- 44. ОборудованиеДва теннисных шарика с небольшим ушком, покрытые
- 45. ПогрешностиОценки погрешности в этой работе не требуется
- 46. ЗаданиеС помощью имеющегося оборудования определите удельное сопротивление воздуха.
- 47. Авторское решениеУдельное сопротивление можно определить по скорости
- 48. ТеорияЗакон Ома в дифференциальной форме: j =
- 49. ЭкспериментПодвешиваем шарики на длинных нитях (ℓ =
- 50. Калибровка
- 51. КалибровкаЗаряжаем шарики с помощью пластмассовой палочки, наэлектризованной
- 52. Основной экспериментВновь заряжаем шарики так, что расстояние
- 53. РезультатыT1/2 ≈ 14 мин = 840 c
- 54. Тянем резинуГук или не Гук ???
- 55. ОборудованиеРезиновый шнур диаметром d0 = 2,5 мм;
- 56. Оборудование (картинка)
- 57. Задание №1Снимите зависимость относительной длины ℓ/ℓ0 резинового
- 58. Установка (например, вот так)
- 59. Задание № 2Выразите коэффициент жёсткости резинового шнура
- 60. Задание № 3Предполагая, что модуль Юнга и
- 61. Теоретическая зависимость ℓ(F)По закону Гука для небольших
- 62. Рабочая формулаℓ/ℓ0 = 1/(1 – F/ES0) –
- 63. Задание № 4Сравните экспериментальную зависимость с теоретической, полученной в П.3
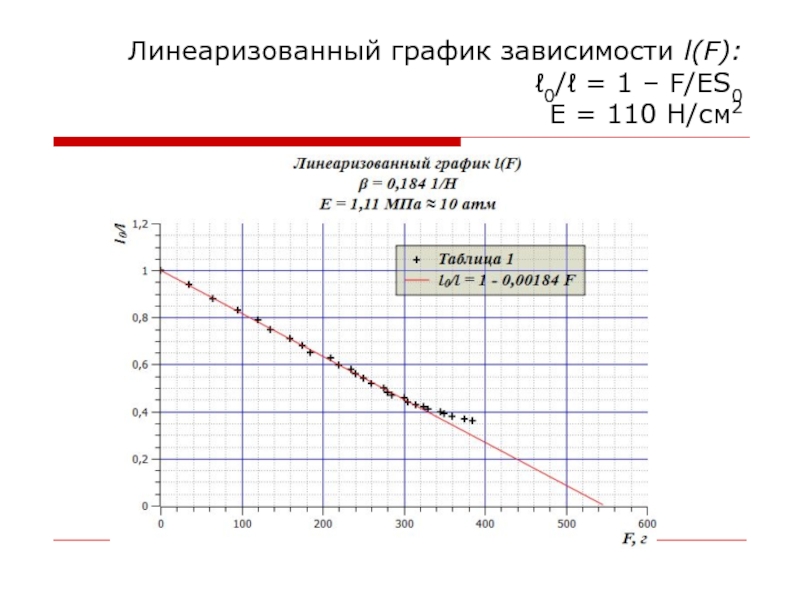
- 64. Линеаризованный график зависимости l(F): ℓ0/ℓ = 1 – F/ES0 E = 110 H/см2
- 65. ВыводыВплоть до деформаций l/l0 ~ 2,5 модуль
- 66. Задание № 7Найдите теоретическое значение коэффициента Пуассона
- 67. При каких μ объём не изменяется? Для
- 68. Задание № 8Определите экспериментально коэффициент Пуассона резины, из которой изготовлен резиновый бинт
- 69. Определяем коэффициент Пуассона (установка)
- 70. Теорияdb/b = -μdℓ/ℓ → b(ℓ): b/b0 =
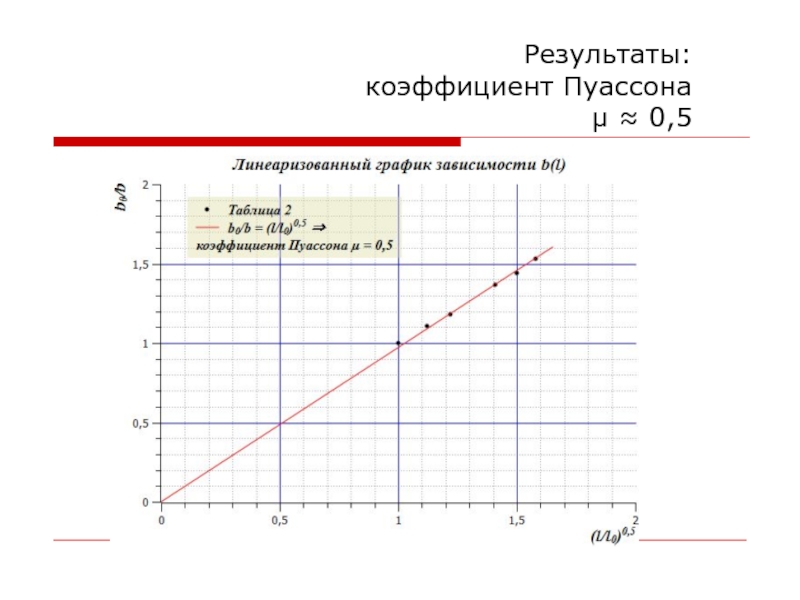
- 71. Результаты: коэффициент Пуассона μ ≈ 0,5
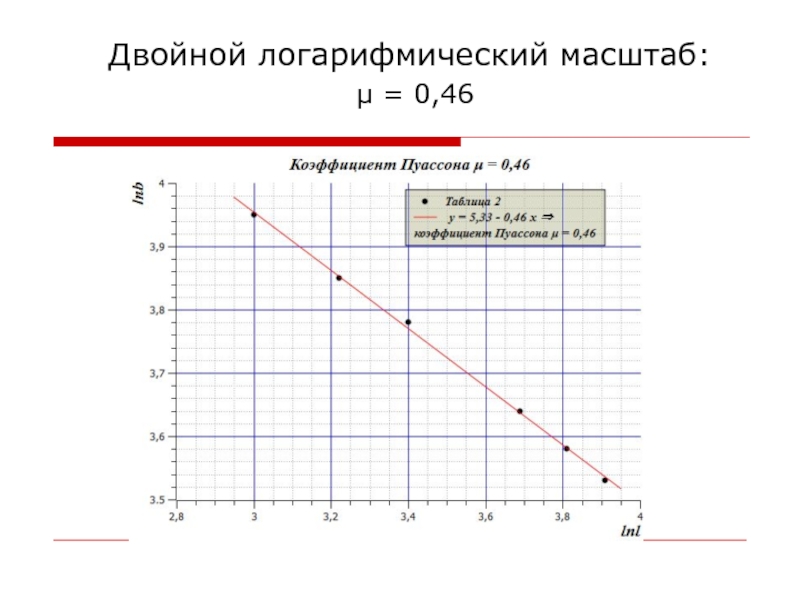
- 72. Двойной логарифмический масштаб: μ = 0,46
- 73. ВСЁ. СПАСИБО
- 74. Скачать презентанцию
Все задачи в предлагаемой презентации - авторские
Слайды и текст этой презентации
Слайд 1Олимпиадный эксперимент – в школьный практикум
Алексей Гуденко
к.ф.м.н.,
доцент кафедры общей
физики МФТИ,
Слайд 3Полезные сайты
Олимпиадная школа МФТИ, курс «Экспериментальная физика»:
http://edu-homelab.ru
Международная олимпиада по
экспериментальной физике (IEPhO): http://iepho.com
Информационный сайт Всероссийской олимпиады по физике:
http://4ipho.ru
Слайд 4Обработка результатов,
графики
Все графики оформлены с помощью программы SciDavis http://scidavis.sourceforge.net
Слайд 5Наши планы
IEPhO-4 (2016 г.)
Неваляшка
Лестница
Лягушка
Зубочистка
Слинки (Slinky)
IEPhO-3 (2015 г.)
Удельное сопротивление воздуха
Гук или не Гук
Слайд 8Задание
С помощью имеющегося оборудования определите как можно точнее высоту центра
тяжести h неваляшки относительно уровня стола, на котором она расположена
Указание:
Основание
неваляшки считать сферическим,неровностями его поверхности пренебречь.
Массу подвижных частей колокольчика внутри
неваляшки считать пренебрежимо малой
Слайд 9Решение. Шаг № 1
По длине окружности C = 283 мм
(Неваляшку оборачиваем бумагой) определяем радиус сферического основания Неваляшки: R =
С/2π = 45 мм.
Слайд 10Шаг № 2
Подбираем кусок пластилина такой массы m, чтобы ось
Неваляшки расположилась горизонтально.
Из условия равновесия относительно точки опоры (точки
касания сферы со столом) получаем:
mgb = MgΔℓ, где b = 100 мм – рычаг куска пластилина, а MgΔℓ - момент силы тяжести Неваляшки (Δℓ - расстояние от центра сферического основания Неваляшки вдоль её оси до центра масс Неваляшки) →
Δℓ = (m/M) b
Цель дальнейших действий - найти отношение m/M. 
Слайд 11Шаг № 3
Уравновешиваем Неваляшку на «рычажных весах», изготовленных из линейки
(рычаг) и карандаша (опора). Из условия равновесия получаем (mл – масса
линейки): Mgℓ1 = mgℓ2 + mлgℓ3 Делаем необходимые измерения: ℓ1 = 49 мм – рычаг Неваляшки; ℓ2 = 341 мм – рычаг пластилина; ℓ3 = 146 мм – рычаг линейки (расстояние от точки опоры до середины линейки). Из уравнения моментов: m/M = ℓ1/(ℓ2 + mл/m ℓ3)
Слайд 12Шаг № 4
Отношение масс линейки и пластилина находим, уравновесив пластилин
линейкой. Из уравнения моментов: mл/m = ℓm/ℓл, где ℓm = 95
мм – рычаг пластилина; ℓл = 100 мм – рычаг линейки. Подставляя численные значения, находим: mл/m = 0,95. Отношение масс пластилина и Неваляшки (см. Шаг № 3): m/M = ℓ1/(ℓ2 + mл/m ℓ3) = 49/(341 + 0,95*146) = 0,102 (точные измерения на весах дают следующие значения масс: масса Неваляшки M = 148 г, масса пластилина: m = 15,26 г → m/M = 0,103 (!))
Слайд 13Заключительный шаг (без картинки)
Центр масс Неваляшки расположен на
Δℓ =
m/M b = 0,102*100 = 10 мм ниже центра сферы
основания, т.е. на высоте: h = R – Δℓ = 35 мм над уровнем стола
Слайд 16Задание
Постройте ступенчатую лестницу максимальной (по горизонтали) длины из n =
2, 3, 4, …12 линеек. Для каждого n измерьте длину
получившейся у вас лестницы и результаты измерений занесите в таблицу, как в абсолютных, так и в относительных единицах.Получите теоретическую зависимость максимальной длины лестницы от числа линеек n.
Сравните теоретические значения c соответствующими экспериментальными значениями.
Оцените максимальную длину лестницы, которую можно составить из линеек всех участников, выполняющих эту работу. Считайте, что работу пишет 20 участников.
Слайд 18Теория:
Δk = ℓ0/2k; ℓТ = ℓ0 + ½ℓ0∑1/k
центр масс
стопки, лежащей над какой-то линейкой, приходится точно на её опорный
край →смещение k-ой сверху линейки относительно (k+ 1)-ой должно удовлетворять условию: mg(ℓ0/2 – Δk) = (k – 1)mgΔk → ширина k-ой ступеньки: Δk = ℓ0/2k
Полная длина лестницы складывается из длины линейки ℓ0 и сумме ширин всех её ступенек: ℓ = ℓ0 + Δ1 + Δ2 + Δ3 + ….
Общая длина лестницы: ℓТ = ℓ0 + ½ ℓ0[1 + ½ + 1/3 + ¼ +…+ 1/(n-1)]
Слайд 19Наши линейки
Δ1=0,5ℓ0/1 = 105 мм
Δ2=0,5ℓ0/2 = 52,5 мм
Δ3 =0,5ℓ0/3 =
35 мм
Δ4=0,5ℓ0/4 = 26,25 мм
Δ5=0,5ℓ0/5 = 21 мм
Δ6=0,5ℓ0/6 = 17,5
ммΔ7=0,5ℓ0/7 = 15 мм
Δ8=0,5ℓ0/8 = 13 мм
Δ9=0,5ℓ0/9 = 11,7 мм
Δ10=0,5ℓ0/10 = 10,5 мм
Δ11=0,5ℓ0/11 = 9,5 мм
Слайд 2012 линеек, 240 линеек
N = 12
ℓT(8)≈ ℓ = ℓ0 +
Δ1 + Δ2 + Δ3 + …. Δ10 + Δ11
≈ 2,51ℓ0 = 52,7 смN = 240 ∑1/k ≈ ∫dz/z ≈ ℓn n
L ≈ ℓ0 + 0,5ℓ0(1+1/2 + 1/3 +…1/11 + ℓnN/11) = ℓ0 + 0,5ℓ0(3,02 + ℓn21,7) = 4,05ℓ0 ≈ 85 см
«Честный» подсчёт:
Слайд 21Лягушка (8, 9 классы)
Оборудование:
кистевой эспандер из мягкой резины («лягушка»),
полиэтилен, дощечка, линейка
Задание:
определите коэффициент трения полиэтилена и «лягушки» о
поверхность дощечки
Слайд 22Решение:
коэффициент трения полиэтилена μп
Кладём «Лягушку» на полиэтилен и по
критическому углу определяем коэффициент трения:
μп = tgαкрит = 0,32
Слайд 23Решение:
коэффициент трения «лягушки» μл
Переворачиваем «установку» и по крит. углу
находим коэффициент трения дощечки по «лягушке»: μл = tg630 ≈ 2
Слайд 24Определение числа π вероятностным методом
(11 класс)
Случайность – форма проявления закономерности
Слайд 25Задача Бюффона
о бросании иглы (1777 г.)
Французский натурфилософ и естествоиспытатель
Иностранный
член Российской Академии наук
член Лондонского королевского общества
Жорж-Луи Леклерк де Бюффон
(Buffon) (1707 – 1788)
Слайд 26Оборудование
10 зубочисток
лист бумаги с параллельными линиями. Расстояние между линиями
равно длине зубочистки ℓ0
Слайд 27Задание
Экспериментально исследовать закон распределения w(n) случайной величины n, где n
– число пересечений зубочисток с линиями при броске n0 =
10 штукПо результатам эксперимента определите число π
Слайд 28Причём здесь π? (теория)
Вероятность пересечь линию для зубочистки, образующей угол
φ (в интервале dφ) с осью x, перпендикулярной линиям: dw =
(|ℓ0x|dφ/2π)/ℓ0 = |cosφ| dφ/2π → wтеор = ∫|cosφ|dφ/2π = 2/π
Слайд 29Как проводим опыт
Одновременно бросаем с высоты ~ 15-20 см n0
= 10 зубочисток и подсчитываем число n пересечений с линиями
в каждом опыте;Делаем N = 40 бросков;
Результаты испытаний заносим в Таблицу
Слайд 35Результат: wтеор = 2/π π = 2/ wэкс = 3,16
± 0,13 (επ = 4 %)
n = 6,33 ± 0,27
– среднее число пересечений, если бросать n0 = 10 штук Вероятность пересечения: wэкс = n/n0 = 0,633 ± 0,027 (εw = 4 %)
Из теории: wтеор = 2/π → πэкс = 2/wэкспер →
π = 3,16 ± 0,13 (επ = 4 %)
Слайд 36Изучение упругих свойств
пластиковой пружины Слинки (Slinky)
Цель работы:
изучение
упругих свойств пластиковой пружины Слинки; исследование колебаний массивной пружины.
Оборудование:
Пластиковая пружина
Слинки (Slinky), штатив с лапкой, линейка, мерная лента, секундомер, весы, скотч.
Слайд 37Задание
(статика)
Снимите зависимость ℓ(n) длины ℓ пружины от числа n
свободно свисающих витков. Для этого закрепите в штативе деревянную линейку.
Разделите линейкой пружину так, чтобы под линейкой оказалось n витков. Для каждого значения n измерьте общую длину свободно свисающих витков. Измерения проведите для n ≥ 10. Результаты измерений занесите в Таблицу №1.Получите теоретическую зависимость ℓ(n), выразив ℓ через массу m0 и жёсткость k0 одного витка
Сравните теоретическую зависимость ℓ(n) с экспериментальной.
Определите m0 и k0
Слайд 38ℓ(n) - теория
Получим теоретическую зависимость ℓ(n), выразив ℓ через массу
m0 и жёсткость k0 одного витка: Δx1 = 0 Δx2 = m0g/k0 Δx3
= 2m0g/k0 ……………… Δxn = (n – 1)m0g/k0 - арифметическая последовательность → ℓ(n) = ΣΔxi = n(n – 1)m0g/2k0 ≈ n2 m0g/2k0, т.е. ℓ = Cn2, где C = m0g/2k0
Слайд 39ℓ(n) - эксперимент
Из графика находим: C = m0g/2k0 = 0,08
см
Определяем m0 и k0.
Масса всей пружины M = 90,37
г, полное число витков N = 41,5 →
масса одного витка: m0 = M/N = 2,18 г;Жёсткость витка: k0 = m0g/2C = 2,18*10-3*9,81/2*0,08*10-2 ≈ 13,4 Н/м.
Слайд 40Задание
(динамика)
Снимите зависимость T(n) периода колебаний T пружины, подвешенной вертикально,
от числа n колеблющихся витков. Измерения проведите для n ≥
10. Результаты измерений занесите в Таблицу №2Считая, что период T колебаний массивной пружины, подвешенной вертикально, определяется формулой T = 2π(βm/k)1/2, где m – масса пружины, k – жёсткость пружины, β – константа, получите теоретическую зависимость T(n).
Сравните теоретическую зависимость T(n) с экспериментальной и определите значение константы βэксп
Сравните экспериментальное значение β с теоретическим.
Слайд 41T(n) - теория
T = 2π(βm/k)1/2 = 2π(βnm0/(k0/n))1/2 = 2πn (βm0/k0)1/2
= An, где A = 2π(βm0/k0)1/2.
Итак T ~ n:
T
= An, где A = 2π(βm0/k0)1/2
Слайд 42T(n) - эксперимент
Итак T ~ n:
T = 0,044n, A =
0,044 c
Находим β:
T2 = 4π2 n2 (2βm0/2k0) = 4π2
n2 (2βm0g/2gk0) ≈ 8βC n2 → 8βC = A2 → βэксп = A2/8C = 0,0442/8*(0,08*10-2) = 0,303βэксп = 0,303
βтеор = 1/3; Δβ/β ≈ 10 %.
Слайд 44Оборудование
Два теннисных шарика с небольшим ушком, покрытые проводящей (графитовой) краской;
пластмассовая трубка; полиэтиленовый пакет; нить; две деревянные линейки; секундомер, скотч,
ножницыПримечание: в качестве вспомогательного оборудования можно использовать стол, стул, а также элементы конструкции вашей кабинки
Слайд 47Авторское решение
Удельное сопротивление можно определить по скорости уменьшения заряда шарика:
q(t) = q0exp(-t/τ)
τ=ρε0 – время релаксации (Максвелловская релаксация)
Слайд 48Теория
Закон Ома в дифференциальной форме:
j = 1/ρ E
Заряд
изменяется (убывает) со скоростью: dq/dt = - ∫jdS = -1/ρ ∫EdS
= {теорема Гаусса} = - 1/ρε0 q Дифферециальное уравнение для q: dq/dt = -q/ρε0 = -q/τ dq/q = -t/τ
q(t) = q0exp(-t/τ)
Слайд 49Эксперимент
Подвешиваем шарики на длинных нитях (ℓ = 130 см). Расстояние
между нитями = d (диаметр шарика ) Незаряженные шарики при
этом слегка соприкасаютсяНа высоте ~ 20 см от шариков подвешиваем линейку в горизонтальном положении.
Слайд 51Калибровка
Заряжаем шарики с помощью пластмассовой палочки, наэлектризованной трением о полиэтиленовый
пакет. Измеряем расстояние между нитями на высоте линейки: d1 ≈
80 мм.Разряжаем один из шариков, коснувшись его рукой. После соприкосновения между собой шарики расходятся так, что расстояние между нитями на уровне линейки оказывается равным d ≈ 60 мм. Заряды шариков при этом уменьшаются вдвое.
Калибровка проведена.
Слайд 52Основной эксперимент
Вновь заряжаем шарики так, что расстояние между нитями, отсчитанное
по линейке, вновь становится равным d1= 80 мм.
С помощью
секундомера измеряем время T1/2, за которое расстояние между нитями уменьшается до d2= 60 мм. Это время соответствует уменьшению заряда вдвое. 
Слайд 53Результаты
T1/2 ≈ 14 мин = 840 c
τ =
ρε0 = T1/2/ℓn2 ρ = T1/2/ε0ℓn2 = 840/8,85*10-12*0,7 ≈
1,4*1014 Ом мρ ≈ 1,4*1014 Ом м
ρтабл ≈ (1-2)*1014 Ом м
Слайд 55Оборудование
Резиновый шнур диаметром d0 = 2,5 мм; резиновая лента (бинт);
динамометр; две канцелярские клипсы; две струбцины; четыре деревянных бруска (два
из них – с саморезами); мерная лента; линейка; ножницы; скотч.
Слайд 57Задание №1
Снимите зависимость относительной длины ℓ/ℓ0 резинового шнура от приложенной
силы F вплоть до значений ℓ ~ 3ℓ0, где ℓ0
– длина недеформированного куска шнура.
Слайд 59Задание № 2
Выразите коэффициент жёсткости резинового шнура через модуль Юнга
и его геометрические параметры.
Решение:
По закону Гука:
Δℓ/ℓ = ΔF/ES →
ΔF = (ES/ℓ) Δℓ = kΔℓ →
k = ES/ℓ,
где S = πd2/4 – поперечное сечение цилиндрического шнура 
Слайд 60Задание № 3
Предполагая, что модуль Юнга и объём резины в
процессе деформации не изменяются, получите теоретическую зависимость ℓ/ℓ0 от F
Слайд 61Теоретическая зависимость ℓ(F)
По закону Гука для небольших деформаций:
∂ℓ/ℓ = ∂F/ES
→ ∂ℓ/ℓ2 = ∂F/ESℓ = ∂F/EV0. V = Sℓ = S0ℓ0
= πd02ℓ0/4 – объём ℓ0, d0 – длина и диаметр S0 = πd02/4 - площадь сечения недеформированного шнура. Интегрируем уравнение: ∂ℓ/ℓ2 = ∂F/EV0 → 1/ℓ0 – 1/ℓ = F/EV0 →
Слайд 62Рабочая формула
ℓ/ℓ0 = 1/(1 – F/ES0) –
зависимость ℓ(F) при
условии, что:
модуль Юнга E = const
объём резины V =
const
Слайд 65Выводы
Вплоть до деформаций l/l0 ~ 2,5 модуль Юнга резины в
пределах точности эксперимента является постоянной величиной E = (110 ±
10) Н/см2 (~ 10 бар)Для справки: Сталь: E = 2 1011 Па = 2 Мбар Медь: E = 1,3 1011 Па = 1,3 Мбар Лёд: E = 3 1010 Па = 0,3 Мбар
Слайд 66Задание № 7
Найдите теоретическое значение коэффициента Пуассона μ, при котором
объём резинового шнура при деформациях не изменяется.
Слайд 67При каких μ объём не изменяется?
Для шнура цилиндрической формы
длиной ℓ и диаметром d объём: V = πℓd2/4 =
πℓ0 d02/4 → (d/d0)2 = ℓ0/ℓ → 2Δd/d = - Δℓ/ℓ → Δd/d = - ½ Δℓ/ℓ → μ = - ½ - при таком значении коэффициента Пуассона объём материала при его деформациях не изменяется.
Слайд 68Задание № 8
Определите экспериментально коэффициент Пуассона резины, из которой изготовлен
резиновый бинт
Слайд 70Теория
db/b = -μdℓ/ℓ → b(ℓ):
b/b0 = -(ℓ/ℓ0)μ
lnb = C
– μℓnℓ → в двойном логарифмическом масштабе тангенс угла наклона
прямой b(ℓ) равен коэффициенту Пуассона
