Операторный метод анализа переходных процессов

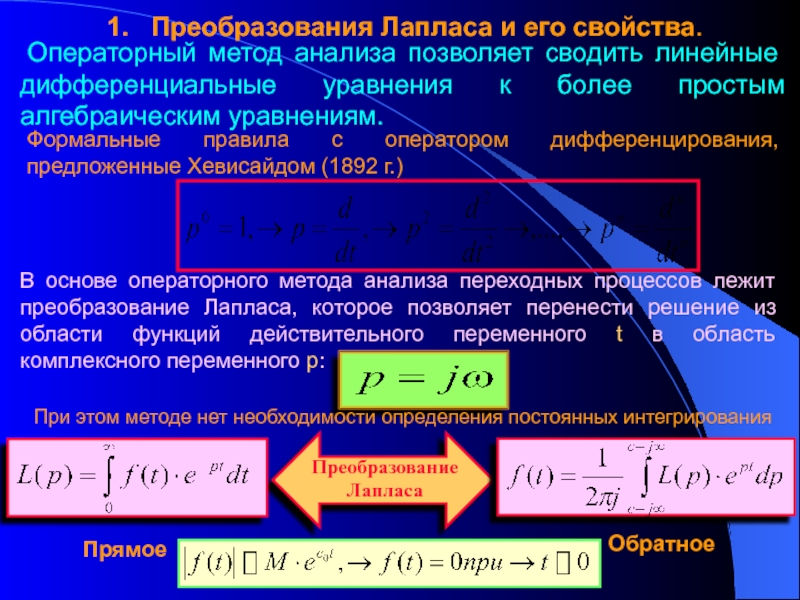
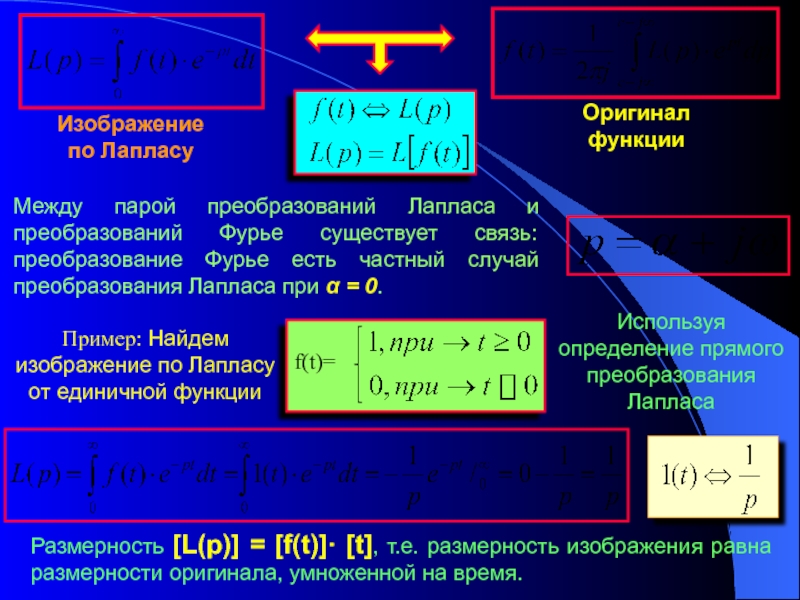
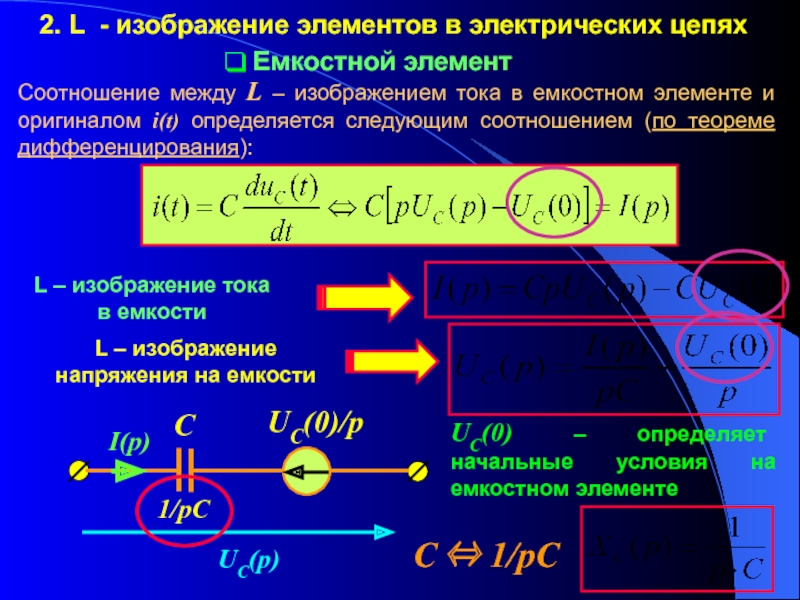
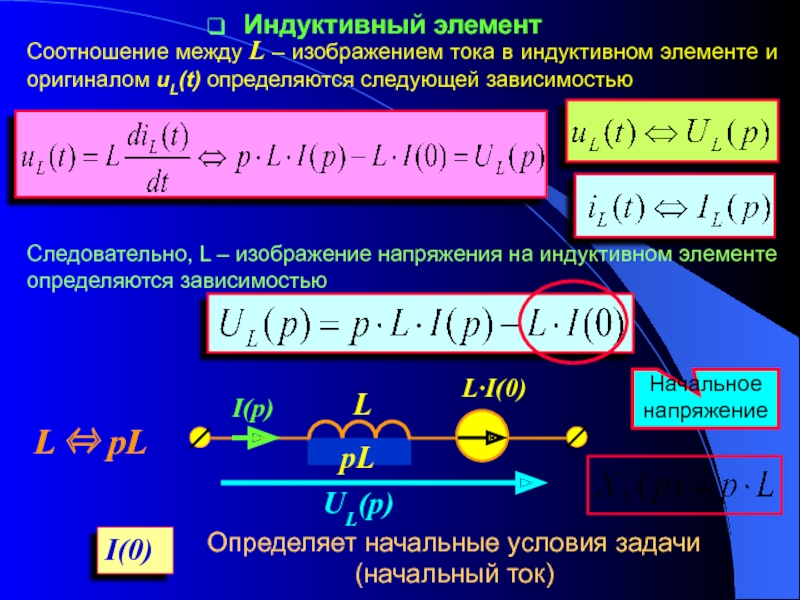
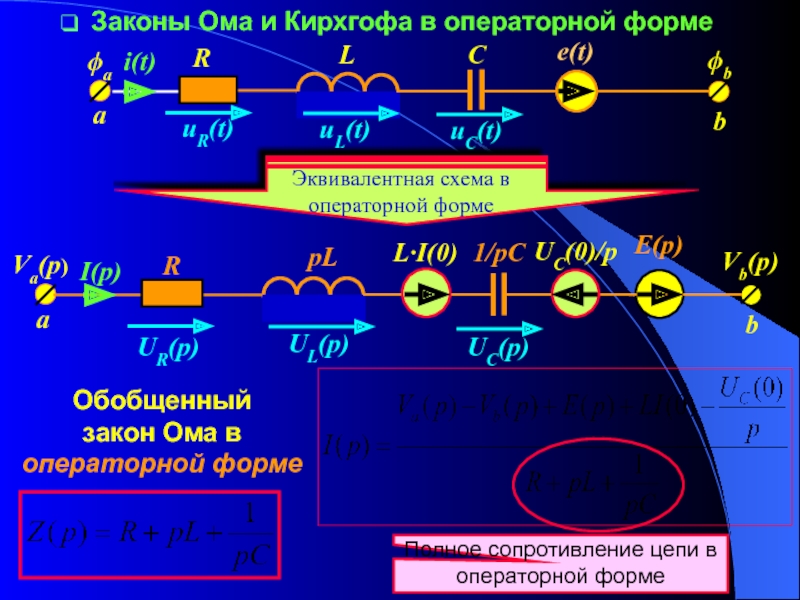
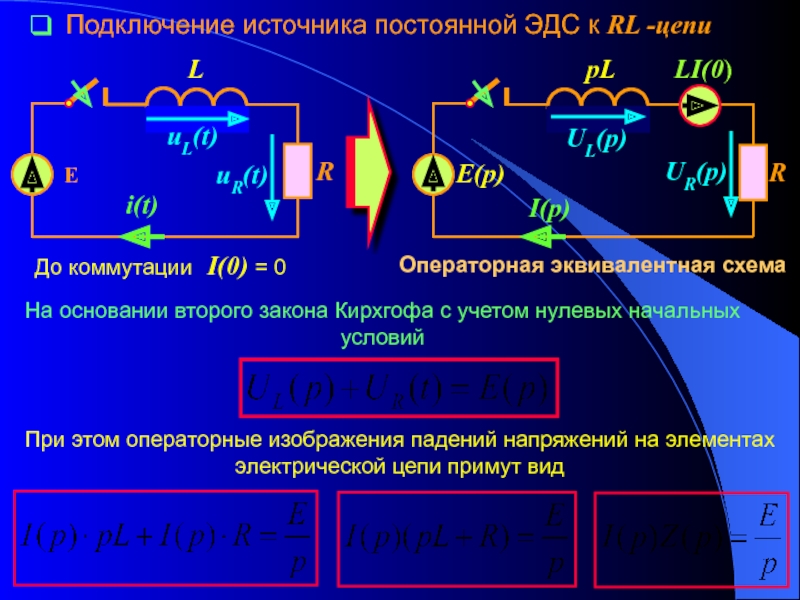
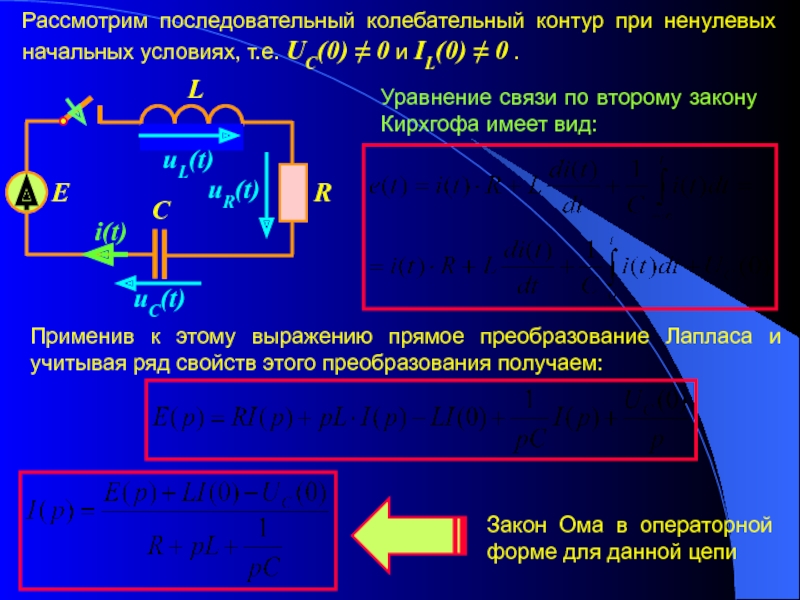
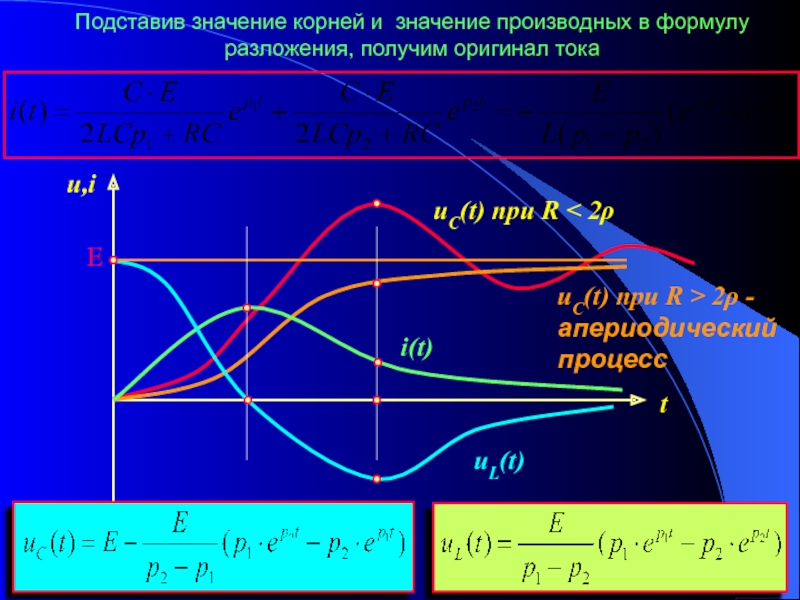
переходных процессов
Кубанский государственный технологический университет
Кафедра компьютерных технологий и информационной

Институт информационных технологий и безопасности

элементов в электрических цепях.
3. Методика анализа переходных процессов в

Литература:

1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 185 –187.

2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 121 –132.

3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.: Высшая школа, 2003 г, с. 114 –122.

позволяет сводить линейные дифференциальные уравнения к более простым алгебраическим уравнениям.
Формальные

В основе операторного метода анализа переходных процессов лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительного переменного t в область комплексного переменного p:

При этом методе нет необходимости определения постоянных интегрирования

Фурье есть частный случай преобразования Лапласа при α = 0.
Пример:

Используя определение прямого преобразования Лапласа

Размерность [L(p)] = [f(t)]· [t], т.е. размерность изображения равна размерности оригинала, умноженной на время.

таких сигналов, которые могут быть представлены суммами относительно простых слагаемых

2. Дифференцирование оригинала

3. Интегрирование оригинала

4. Теорема запаздывания

5. Теорема смещения

цепей в операторной форме.

между L – изображением тока в емкостном элементе и оригиналом

L – изображение тока в емкости

L – изображение напряжения на емкости

UC(0) – определяет начальные условия на емкостном элементе

С ⇔ 1/pС

индуктивном элементе и оригиналом uL(t) определяются следующей зависимостью
Следовательно, L –

I(0)

Определяет начальные условия задачи (начальный ток)

Начальное напряжение

L ⇔ pL

напряжение на емкостном элементе
Операторное напряжение на индуктивном элементе
Операторные сопротивление и

Операторные сопротивление и проводимость индуктивного элемента

Резистивный элемент

закон Ома в операторной форме

Полное сопротивление цепи

в узле равна нулю

Второй закон Кирхгофа в операторной форме
Методика

1. Из расчета цепи до коммутации найти токи в индуктивности IL(0) и напряжения на емкости UC(0).

2. По виду топологии исследуемой цепи, получившейся после коммутации, составить эквивалентную операторную схему.

3. Выбрать метод расчета и найти изображение искомых величин.

4. По изображению искомых величин (с помощью таблицы преобразований Лапласа) найти оригинал, т.е. искомую функцию

Алгебраическая сумма операторных падений напряжений в контуре равна алгебраической сумме операторных ЭДС и напряжений контура

= 0
Операторная эквивалентная схема
На основании второго закона Кирхгофа с учетом

При этом операторные изображения падений напряжений на элементах электрической цепи примут вид

и затем его предельное значение

Переходный процесс заканчивается через время →

≠ 0 и IL(0) ≠ 0 .
Уравнение связи по второму

Применив к этому выражению прямое преобразование Лапласа и учитывая ряд свойств этого преобразования получаем:

Закон Ома в операторной форме для данной цепи

по закону Ома для нулевых начальных условий примет вид:
Определим корни

Воспользовавшись теоремой разложения, которая позволяет при нахождении оригинала операцию интегрирования заменить операцией суммирования, что значительно упрощает расчеты

pk – корни характеристического уравнения

оригинал тока

uC(t) при R < 2ρ



i(t)
uL(t)
uC(t) при R >

изображений выходной реакции электрической цепи к изображению входного воздействия
В связи

Передаточная функция по напряжению

Передаточная функция по току

Передаточная функция сопротивления

Передаточная функция проводимости

Комплексные передаточные функции (p ⇒ jω) – частотный метод анализа

цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с.

2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 121 –132.

3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.: Высшая школа, 2003 г, с. 114 –122.

Задание на самостоятельную работу