Описание движения материальной точки

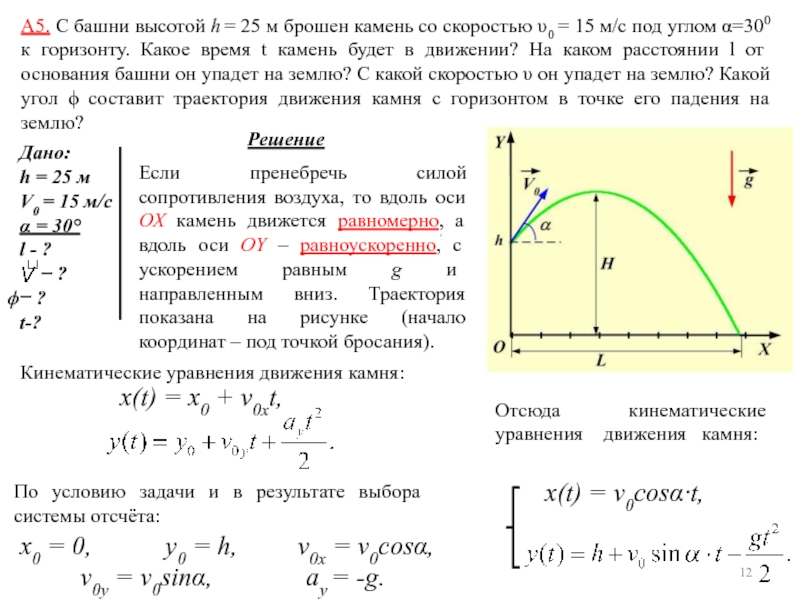
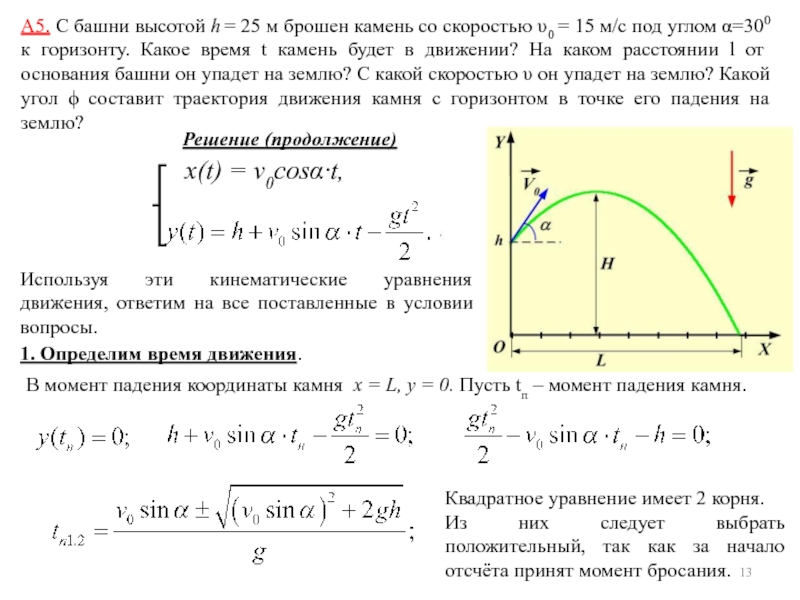
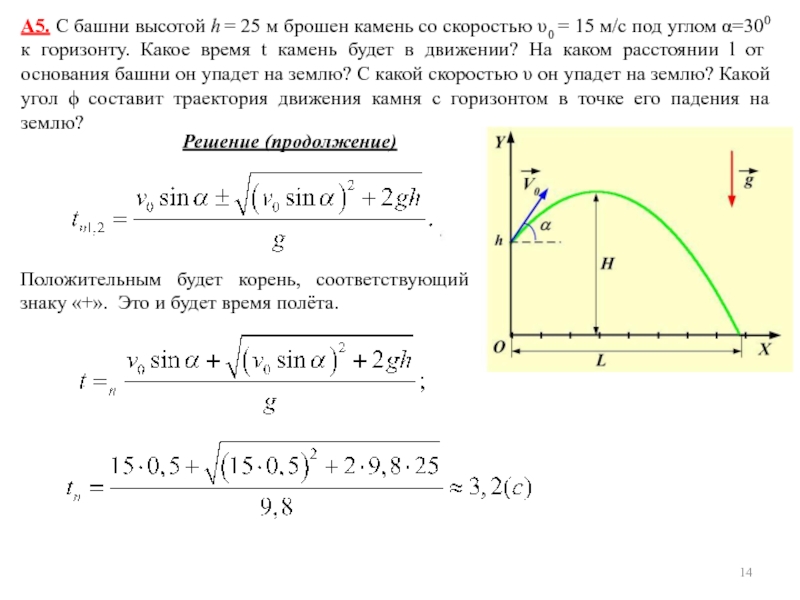
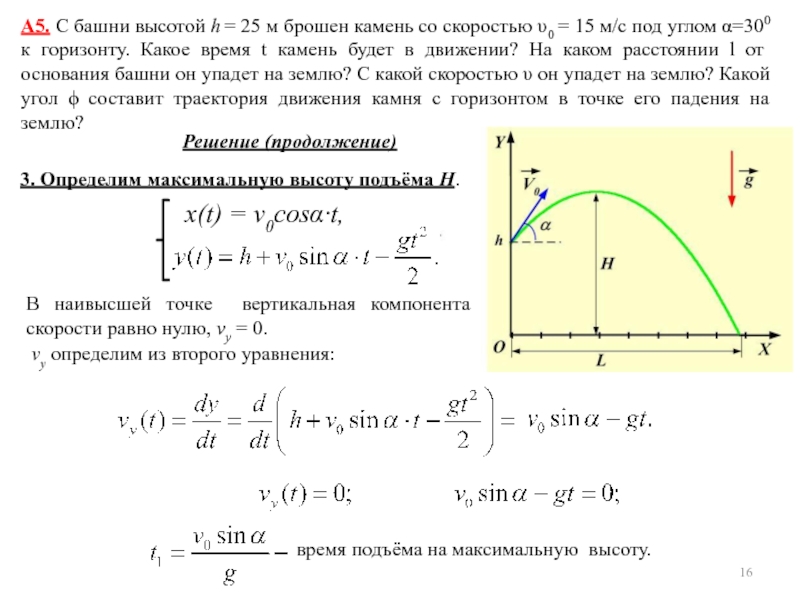
уравнением s = A + Bt + Ct2 + Dt3,

Дано:
s = A + Bt+Ct2+Dt3
B = 0,01 м/с
C = 0,14 м/c2
D = 0,01 м/с3
a = a0 = 1 м/с2
v - ?
- ?

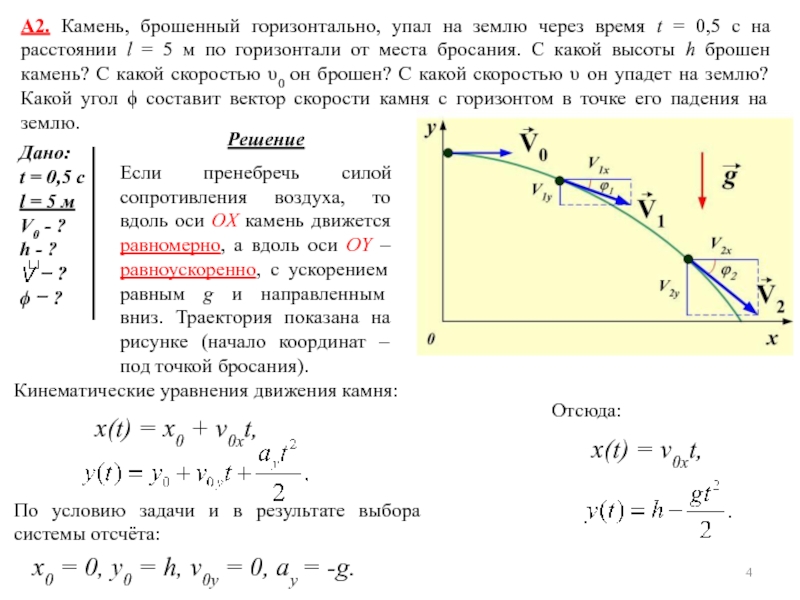
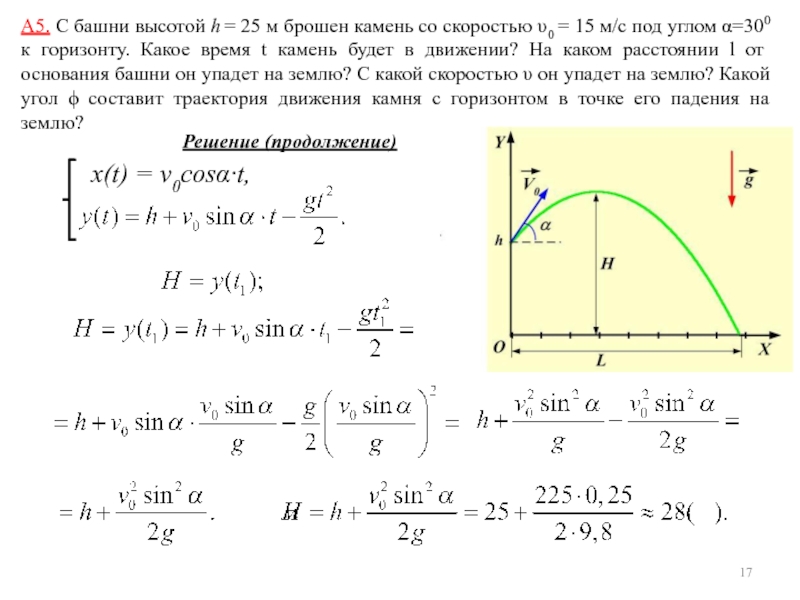
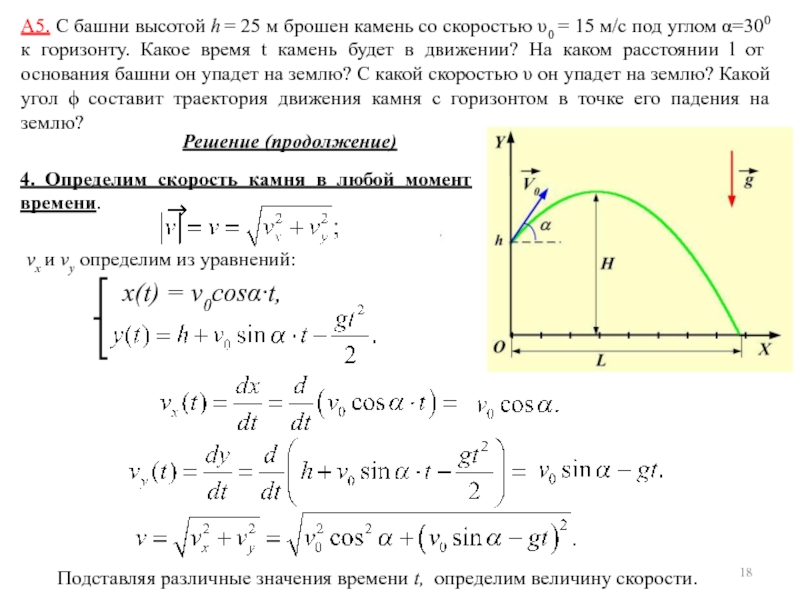
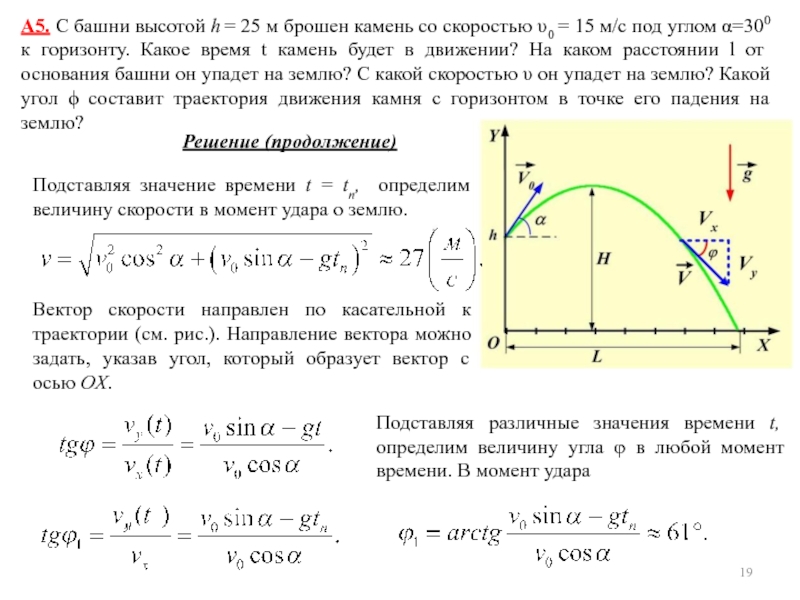
Материальная точка движется прямолинейно. Выберем ось OX направленной вдоль траектории точки. В этом случае величина пройденного пути равна s = x(t) - x(t0).

x(t) = A + Bt+Ct2 + Dt3.

Начало координат выберем так, что x(t0) = 0. Тогда кинематическое уравнение движения имеет вид:

Проекция скорости на ось OX:

Проекция ускорения на ось OX:

По условию ax = a0 = 1 м/с, поэтому

уравнением s = A + Bt + Ct2 + Dt3,

Ответ: t = 12 c; = 0,64 м/с2.

t = 0,5 с на расстоянии l = 5 м

Дано:
t = 0,5 c
l = 5 м
V0 - ?
h - ?
− ?
ϕ − ?

Решение

Если пренебречь силой сопротивления воздуха, то вдоль оси OX камень движется равномерно, а вдоль оси OY – равноускоренно, с ускорением равным g и направленным вниз. Траектория показана на рисунке (начало координат – под точкой бросания).

Кинематические уравнения движения камня:

x(t) = v0xt,

x(t) = x0 + v0xt,

По условию задачи и в результате выбора системы отсчёта:

x0 = 0, y0 = h, v0y = 0, ay = -g.

Отсюда:

t = 0,5 с на расстоянии l = 5 м

Решение (продолжение)

x(t) = v0xt,

Итак, кинематические уравнения движения

Когда камень упадёт на землю,
x = l, y = 0 (см. рис.).

x(t) = v0xt = l,

t = 0,5 с на расстоянии l = 5 м

Решение (продолжение)

x(t) = v0xt,

Из уравнений движения определим, как зависят от времени проекции скорости на оси координат.

Величина скорости в любой момент времени:

Величина скорости в момент падения (t = 0,5 c):

t = 0,5 с на расстоянии l = 5 м

Решение (продолжение)

x(t) = v0xt,

Тангенс угла, образуемого вектором скорости с осью OX в любой момент времени (см. рис.):

В момент падения (t = 0,5 c):

Ответ: h = 1,25 м; v0 = 10 м/с, v = 11,1 м/с, φ = 26˚.

Найти нормальное аn и тангенциальное аτ ускорения камня через время

Дано:
υ0 = 15 м/с
t = 1 с
аn - ?
аτ - ?

Решение

Вектор ускорения камня во время полёта всегда направлен вниз, а по величине равен g (см.рис.).

Вектор ускорения камня можно представить, как сумму двух векторов, перпендикулярных друг другу

Углы между вектором скорости и осью OX и векторами полного и нормального ускорения равны, как острые углы со взаимно перпендикулярными сторонами (см.рис.).

Найти нормальное аn и тангенциальное аt ускорения камня через время

Решение (продолжение)

Камень падает в поле силы тяжести и воль оси OX движется равномерно, а вдоль оси OY – с постоянным ускорением g. Проекции скорости камня зависят от времени так (см. решение предыдущей задачи):

Подставим выражения для модулей проекций скорости в формулы для an и at:

Ответ: an = 8,2 м/c2; at = 5,4 м/с2.

Найти радиус кривизны R траектории камня через время t =

Дано:
υ0 = 10 м/с
t = 3 с
R - ?

Решение

Вектор ускорения камня во время полёта всегда направлен вниз, а по величине равен g (см.рис.).

Вектор ускорения камня можно представить, как сумму двух векторов, перпендикулярных друг другу

Углы между вектором скорости и осью OX и векторами полного и нормального ускорения равны, как острые углы со взаимно перпендикулярными сторонами (см.рис.).

Найти радиус кривизны R траектории камня через время t =

Решение (продолжение)

Согласно определению величина нормального (центростремительного) ускорения равна

где R – радиус кривизны траектории.

Ответ: R = 305 м.

со скоростью υ0 = 15 м/с под углом α=300 к

Дано:
h = 25 м
V0 = 15 м/с
α = 30°
l - ?
− ?
− ?
t-?

Решение

Если пренебречь силой сопротивления воздуха, то вдоль оси OX камень движется равномерно, а вдоль оси OY – равноускоренно, с ускорением равным g и направленным вниз. Траектория показана на рисунке (начало координат – под точкой бросания).

Кинематические уравнения движения камня:

x(t) = v0cosα·t,

x(t) = x0 + v0xt,

По условию задачи и в результате выбора системы отсчёта:

x0 = 0, y0 = h, v0x = v0cosα,
v0y = v0sinα, ay = -g.

Отсюда кинематические уравнения движения камня:

со скоростью υ0 = 15 м/с под углом α=300 к

Решение (продолжение)

x(t) = v0cosα·t,

Используя эти кинематические уравнения движения, ответим на все поставленные в условии вопросы.

1. Определим время движения.

В момент падения координаты камня x = L, y = 0. Пусть tп – момент падения камня.

Квадратное уравнение имеет 2 корня.
Из них следует выбрать положительный, так как за начало отсчёта принят момент бросания.

со скоростью υ0 = 15 м/с под углом α=300 к

Решение (продолжение)

Положительным будет корень, соответствующий знаку «+». Это и будет время полёта.

со скоростью υ0 = 15 м/с под углом α=300 к

Решение (продолжение)

x(t) = v0cosα·t,

2. Определим дальность полёта L.

В момент падения координаты камня x = L, y = 0.
L и есть дальность полёта. Эти значения координат достигаются в момент t = tп.

со скоростью υ0 = 15 м/с под углом α=300 к

Решение (продолжение)

3. Определим максимальную высоту подъёма H.

x(t) = v0cosα·t,

В наивысшей точке вертикальная компонента скорости равно нулю, vy = 0.

vy определим из второго уравнения:

время подъёма на максимальную высоту.

со скоростью υ0 = 15 м/с под углом α=300 к

Решение (продолжение)

x(t) = v0cosα·t,

со скоростью υ0 = 15 м/с под углом α=300 к

Решение (продолжение)

4. Определим скорость камня в любой момент времени.

x(t) = v0cosα·t,

vx и vy определим из уравнений:

Подставляя различные значения времени t, определим величину скорости.

со скоростью υ0 = 15 м/с под углом α=300 к

Решение (продолжение)

Подставляя значение времени t = tп, определим величину скорости в момент удара о землю.

Вектор скорости направлен по касательной к траектории (см. рис.). Направление вектора можно задать, указав угол, который образует вектор с осью OX.

Подставляя различные значения времени t, определим величину угла φ в любой момент времени. В момент удара

выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75

Дано:
ν = 900 об/мин
ω = 0
N = 75 об
t - ?

Решение

Выберем систему отсчёта, как показано на рисунке. Направления векторов скорости, угловой скорости и углового ускорения – на рисунке. Перейдём к полярным координатам.

Вентилятор движется замедленно. Кинематическое уравнение движения:

Проекция угловой скорости вентилятора:

Определим значения параметров уравнения:

выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75

Решение (продолжение)

Уравнения движения в полярных координатах:

Из второго уравнения выразим ε :

Когда вентилятор остановится,

Когда вентилятор остановится, проекция углового перемещения составит

выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75

Решение (продолжение)

Время до остановки:

Ответ: t = 10 с.

с постоянным тангенциальным ускорением аτ. Найти тангенциальное ускорение аτ точки,

Дано:
R = 20 см
аτ = const.
υ = 79,2 cм/с
аτ - ?

Решение

Тангенциальная составляющая ускорения направлена, как и вектор скорости, по касательной к траектории. Поэтому она «ответственна» за изменение модуля линейной скорости. Тангенциальная составляющая ускорения постоянна по величине.

(S – путь, пройденный материальной точкой)

с постоянным тангенциальным ускорением аτ. Найти тангенциальное ускорение аτ точки,

Решение (продолжение)

Путь, пройденный точкой,

N – число оборотов.

Ответ:

=3,14 рад/с2. Найти для точек на ободе колеса к концу

Дано:
R=10 см
ε =3,14 рад/с2
t = 1 с
ω - ?
υ - ?
аτ - ?
аn - ?
α - ?

Решение

Направления векторов скорости, угловой скорости и углового ускорения – на рисунке. Перейдём к полярным координатам. Колесо движется с постоянным угловым ускорением. Кинематическое уравнение движения:

Проекция угловой скорости колеса:

Определим значения параметров уравнения:

=3,14 рад/с2. Найти для точек на ободе колеса к концу

Решение (продолжение)

Проекция угловой скорости

Вектор линейной скорости

Направления векторов показаны на рисунке. Для модулей

Тангенциальная составляющая ускорения

Направления совпадает с направлением вектора скорости. Для модулей

=3,14 рад/с2. Найти для точек на ободе колеса к концу

Решение (продолжение)

Нормальная составляющая ускорения направлена к центру окружности . Её величина

Величину полного ускорения найдём по теореме Пифагора (см. рис).

Нормальная составляющая ускорения направлена вдоль радиуса, тангенциальная – по касательной к окружности, поэтому угол между радиусом и вектором ускорения можно определить так:

так, что зависимость криволинейной координаты, отсчитанной вдоль окружности, от времени

Решение

Дано:
B = 2 м/с
C = 1 м/с2
t1 = 3 c
R = 1 м
V - ?
an - ?
at - ?

Проанализируем уравнение движения точки. При этом перемещение против часовой стрелки положительно, по часовой стрелке – отрицательно.

По условию B = 2 м/с, С = 1 м/с2,

при

Скорость, направленная по касательной к окружности

1. При

См. рис 1.

2. При

См. рис 2.

Тангенциальное ускорение

так, что зависимость криволинейной координаты, отсчитанной вдоль окружности, от времени

Решение (продолжение)

Момент времени t = 3 c соответствует ситуации, показанной на рис. 2.

Величина полного ускорения

ободе вращающегося колеса, больше ее тангенциального ускорения аτ для того

Дано:
α = 30°
аn/ аτ - ?

Решение

следовательно,

Ответ: