Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определенный интеграл и его геометрический смысл
Содержание
- 1. Определенный интеграл и его геометрический смысл
- 2. Фигура, ограниченная графиком функции y = f(x)
- 3. yyyyxxxx1.4.3.2.
- 4. Геометрический смысл определенного интеграла
- 5. Формула Ньютона- ЛейбницаЕсли f(х) – непрерывная и
- 6. Свойства определенного интеграла
- 7. Свойства определенного интеграла
- 8. Таблица интегралов
- 9. 1. Метод разложения (непосредственное интегрирование).
- 10. Метод разложения (непосредственное интегрирование).
- 11. Слайд 11
- 12. Примеры:
- 13. Пример Вычислить .
- 14. 2. Интегрирование методом подстановки.
- 15. Метод подстановки (замены переменной)
- 16. Слайд 16
- 17. Слайд 17
- 18. Пример
- 19. 3. Интегрирование по частям
- 20. Метод интегрирования по частям
- 21. Слайд 21
- 22. Пример
- 23. Применение определенного интеграла для вычисления площадей плоских фигур
- 24. Используя понятие определенного интеграла, дадим общий метод
- 25. Основные случаи расположения плоской фигурыСлучай I. Фигура
- 26. Случай II. Фигура ограничена осью ОХ, прямыми
- 27. Случай III. Фигура ограничена осью ОХ, прямыми
- 28. Случай IV. Если f(x) 0, φ(x)
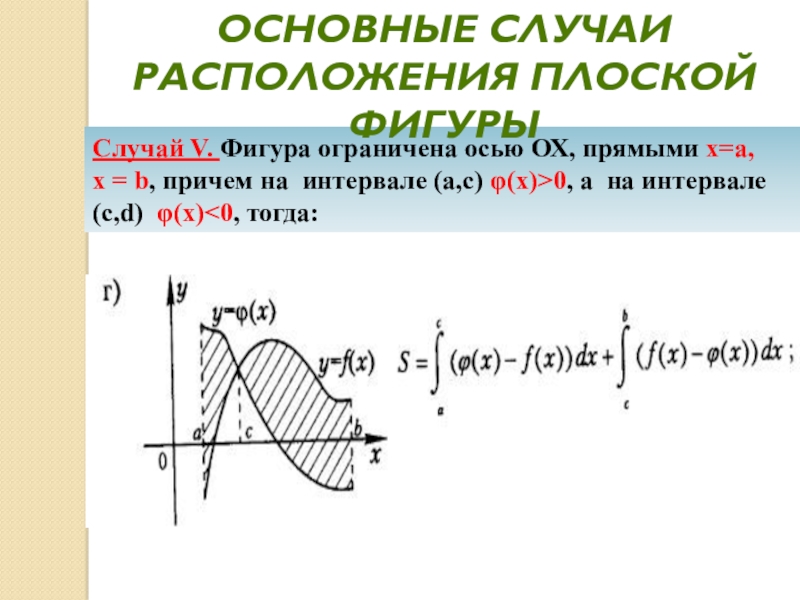
- 29. Случай V. Фигура ограничена осью ОХ, прямыми
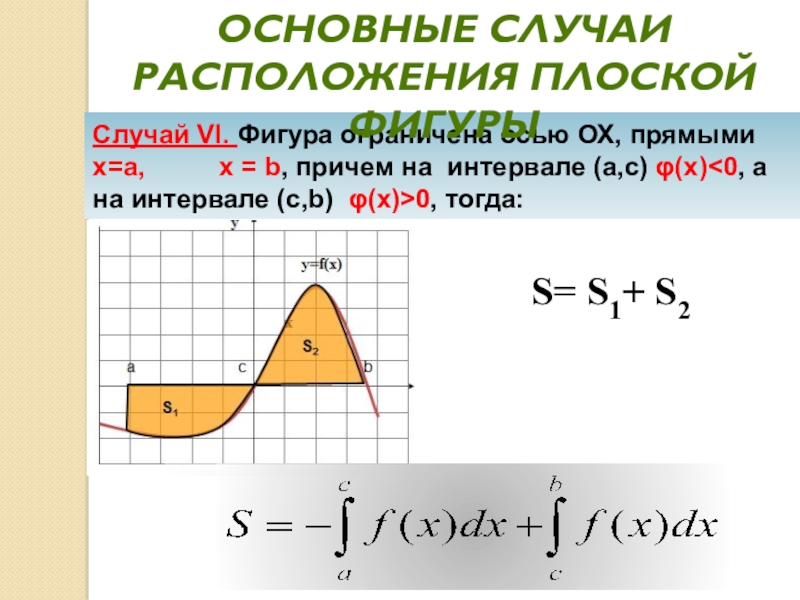
- 30. Случай VI. Фигура ограничена осью ОХ, прямыми
- 31. Сделать чертеж графиков заданных функций, ограничивающих площадь
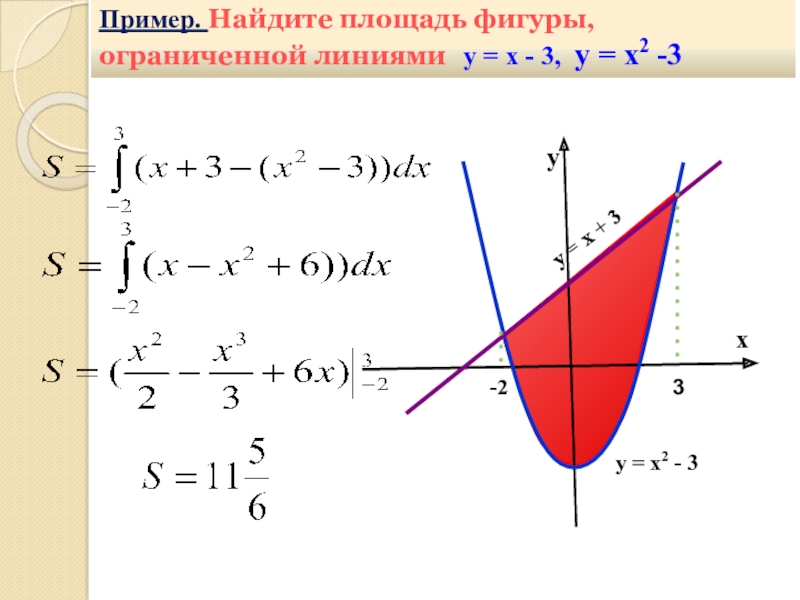
- 32. ху = х2 - 3Пример. Найдите площадь
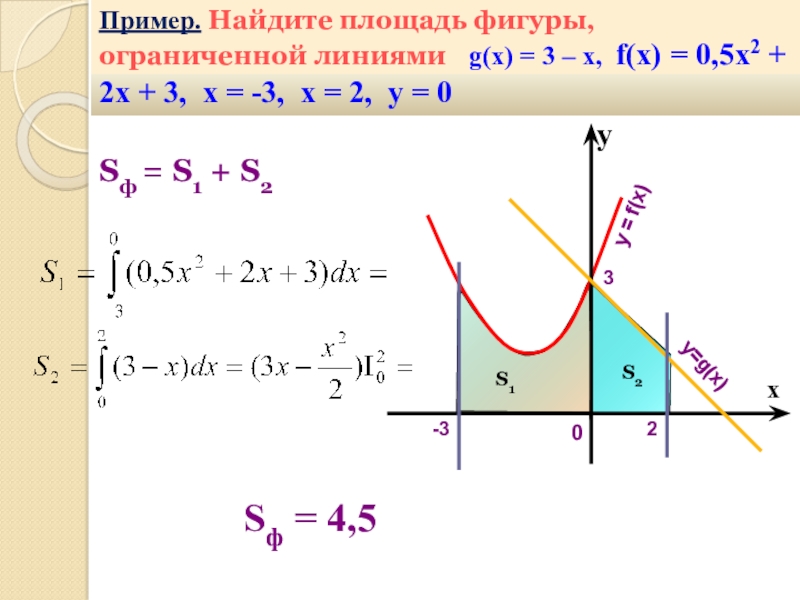
- 33. Пример. Найдите площадь фигуры, ограниченной линиями
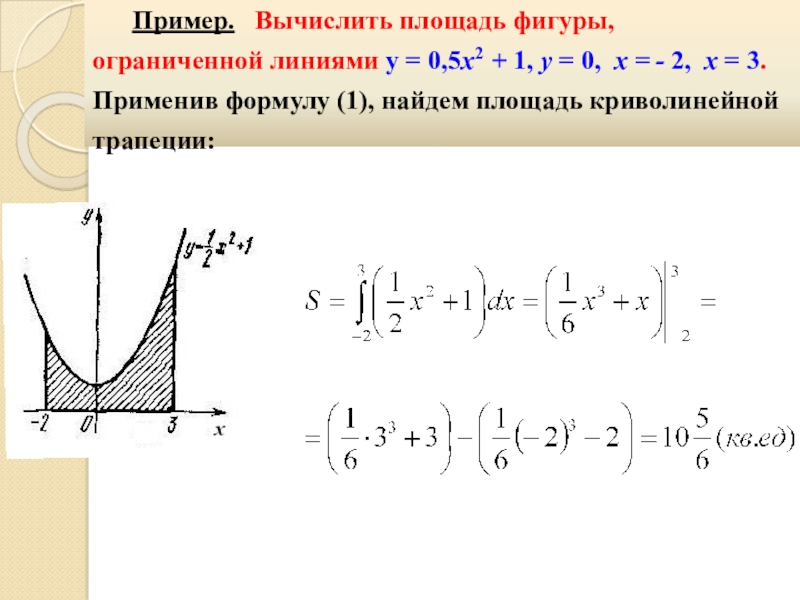
- 34. Пример. Вычислить площадь фигуры, ограниченной
- 35. Пример. Вычислить площадь фигуры, ограниченной линиями
- 36. Пример . Вычислить площадь фигуры, ограниченной
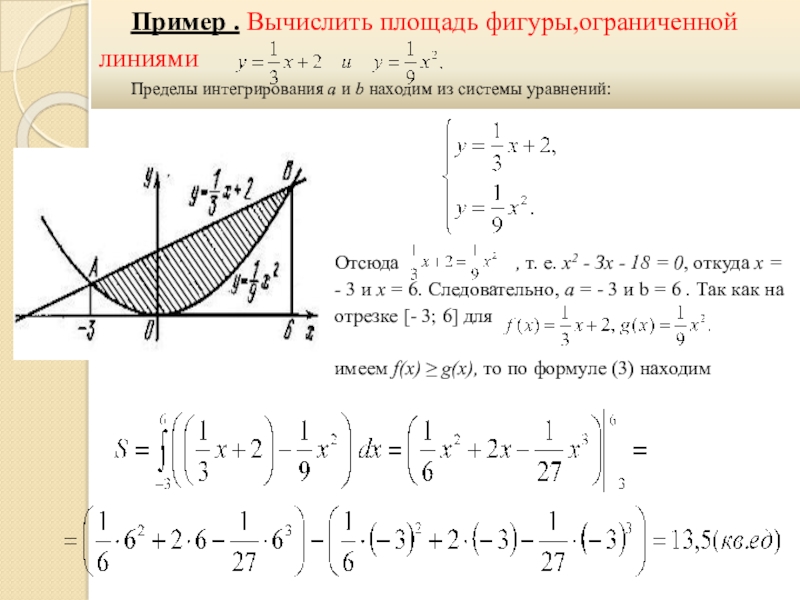
- 37. Пример . Вычислить площадь фигуры,ограниченной линиями
- 38. ФедотоваТамараВалентиновнаСПАСИБО ЗА ВНИМАНИЕ!
- 39. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Определенный интеграл
и его геометрический смысл
Урюпинский филиал
ГАПОУ “Волгоградский медицинский
колледж”
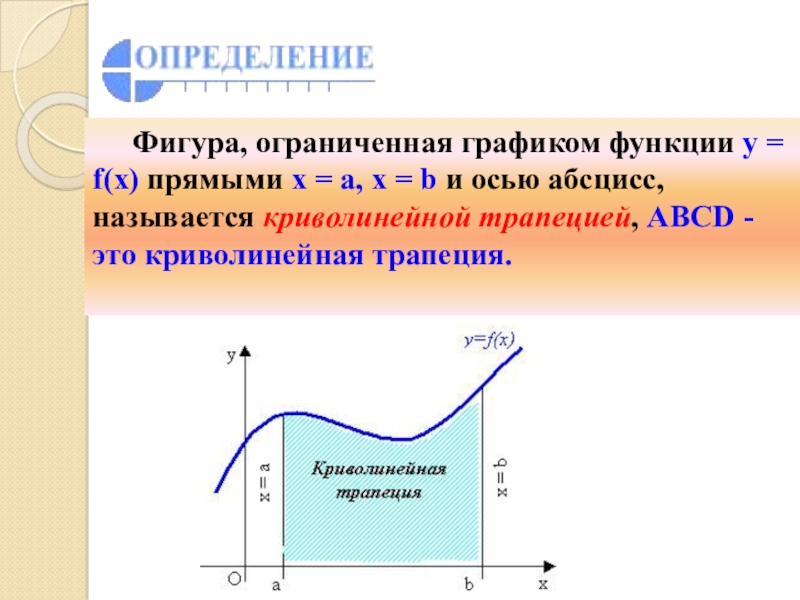
Слайд 2 Фигура, ограниченная графиком функции y = f(x) прямыми x =
a, x = b и осью абсцисс, называется криволинейной трапецией,
ABCD -это криволинейная трапеция.Слайд 5Формула Ньютона- Лейбница
Если f(х) – непрерывная и неотрицательная на отрезке
[a; b] функция , а F(х) – ее первообразная на
этом отрезке , то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a; b] , т.е.Слайд 24Используя понятие определенного интеграла, дадим общий метод вычисления площадей плоских
фигур. Как известно, определенный интеграл от неотрицательной непрерывной функции есть
площадь соответствующей криволинейной трапеции. В этом заключается геометрический смысл определенного интеграла, на этом основано его применение к вычислению площадей плоских фигур.Площадь криволинейной трапеции, ограниченной неотрицательной функцией f (x), осью абсцисс и прямыми x = a, x = b, определяется как
Слайд 25Основные случаи расположения плоской фигуры
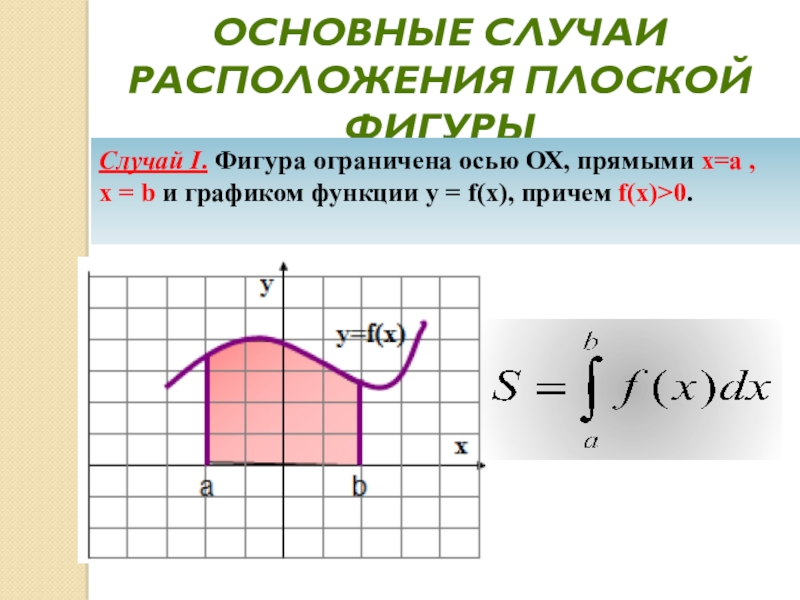
Случай I. Фигура ограничена осью ОХ,
прямыми х=а , х = b и
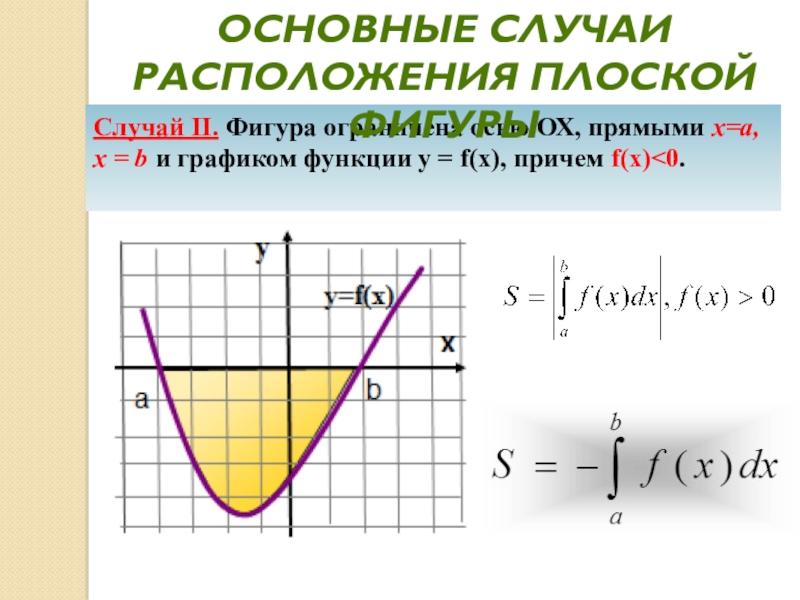
графиком функции у = f(x), причем f(x)>0.Слайд 26Случай II. Фигура ограничена осью ОХ, прямыми х=а, х =
b и графиком функции у = f(x), причем f(x)
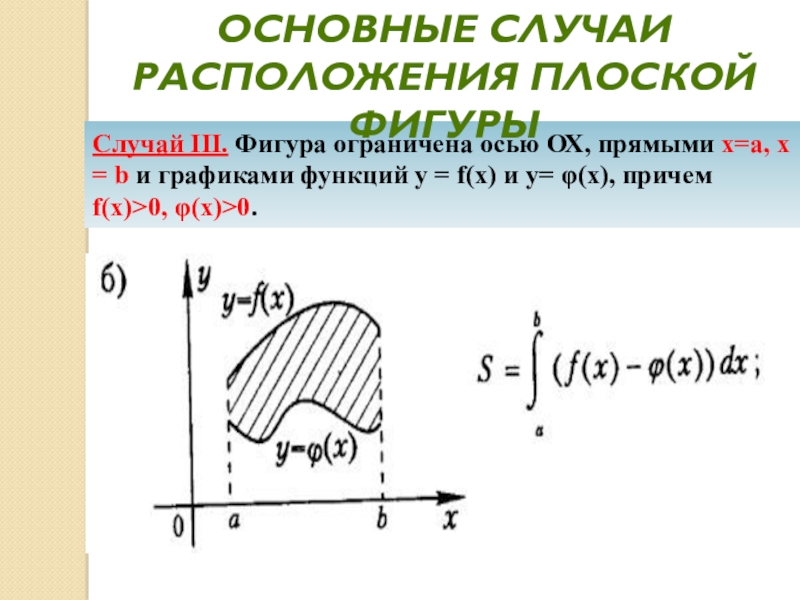
расположения плоской фигурыСлайд 27Случай III. Фигура ограничена осью ОХ, прямыми х=а, х =
b и графиками функций у = f(x) и y= φ(x),
причем f(x)>0, φ(x)>0.Основные случаи расположения плоской фигуры
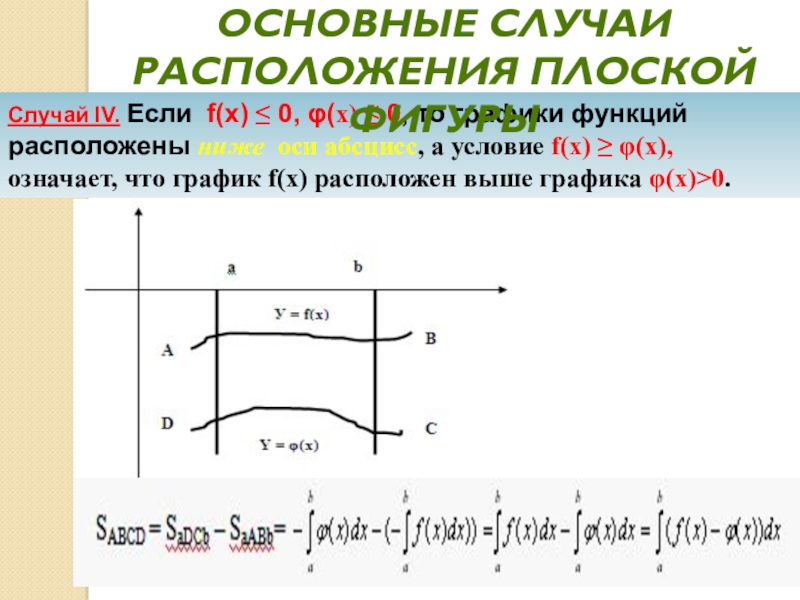
Слайд 28Случай IV. Если f(x) 0, φ(x) 0, то
графики функций расположены ниже оси абсцисс, а условие f(x) ≥
φ(x), означает, что график f(x) расположен выше графика φ(x)>0.Основные случаи расположения плоской фигуры
Слайд 29Случай V. Фигура ограничена осью ОХ, прямыми х=а,
х = b, причем на интервале (а,с) φ(x)>0,
а на интервале (c,d) φ(x)<0, тогда:Основные случаи расположения плоской фигуры
Слайд 30Случай VI. Фигура ограничена осью ОХ, прямыми х=а,
х = b, причем на интервале (а,с) φ(x)
а на интервале (c,b) φ(x)>0, тогда:Основные случаи расположения плоской фигуры
S= S1+ S2
Слайд 31Сделать чертеж графиков заданных функций, ограничивающих площадь плоских фигур.
Найти пределы
интегрирования.
Выяснить какой формулой площади плоской фигуры удобно пользоваться в данном
случае.Вычислить площадь заданной фигуры.
АЛГОРИТМ решения задач на вычисление площадей :
Слайд 33Пример. Найдите площадь фигуры, ограниченной линиями g(x) = 3
– х, f(x) = 0,5х2 + 2х + 3, х
= -3, х = 2, у = 0у
х
S1
S2
Sф = S1 + S2
Sф = 4,5
Слайд 34Пример. Вычислить площадь фигуры, ограниченной линиями y =
0,5х2 + 1, y = 0, х = - 2,
x = 3. Применив формулу (1), найдем площадь криволинейной трапеции:Слайд 35Пример. Вычислить площадь фигуры,
ограниченной линиями y = -
х2 - 1, у = 0, х =-1, х =
2.По формуле (2) находим
Слайд 36Пример . Вычислить площадь фигуры, ограниченной линиями у =
sin х, y = 0, х = -π/2, х =
π . Очевидно, что sin х ≤ 0 для всех х ∈ [- π /2; 0] и sin х ≥ 0 для всех х ∈ [0; π].
Поэтому
Слайд 37Пример . Вычислить площадь фигуры,ограниченной линиями
Пределы интегрирования а и b находим из системы уравнений:
Отсюда , т. е. x2 - Зх - 18 = 0, откуда х = - 3 и х = 6. Следовательно, а = - 3 и b = 6 . Так как на отрезке [- 3; 6] для
имеем f(x) ≥ g(x), то по формуле (3) находим


![Определенный интеграл и его геометрический смысл Формула Ньютона- ЛейбницаЕсли f(х) – непрерывная и неотрицательная на отрезке [a; Формула Ньютона- ЛейбницаЕсли f(х) – непрерывная и неотрицательная на отрезке [a; b] функция , а F(х) –](/img/tmb/7/652961/a677d5e10d9d67038325f18437772cad-800x.jpg)