Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
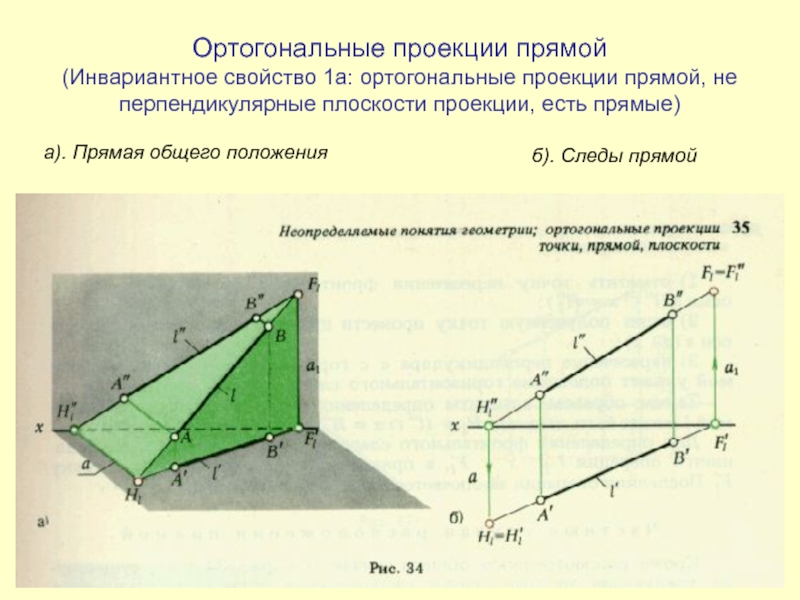
Ортогональные проекции прямой (Инвариантное свойство 1а: ортогональные проекции
Содержание
- 1. Ортогональные проекции прямой (Инвариантное свойство 1а: ортогональные проекции
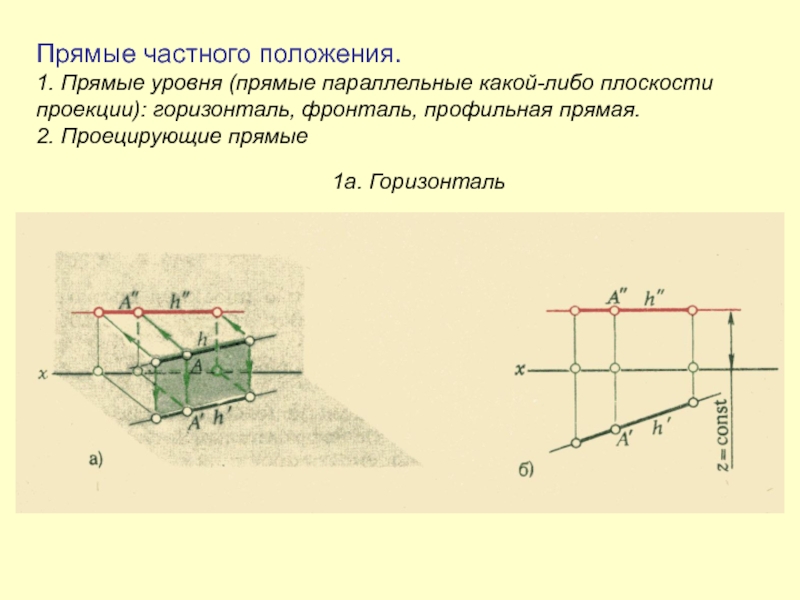
- 2. Прямые частного положения. 1. Прямые уровня
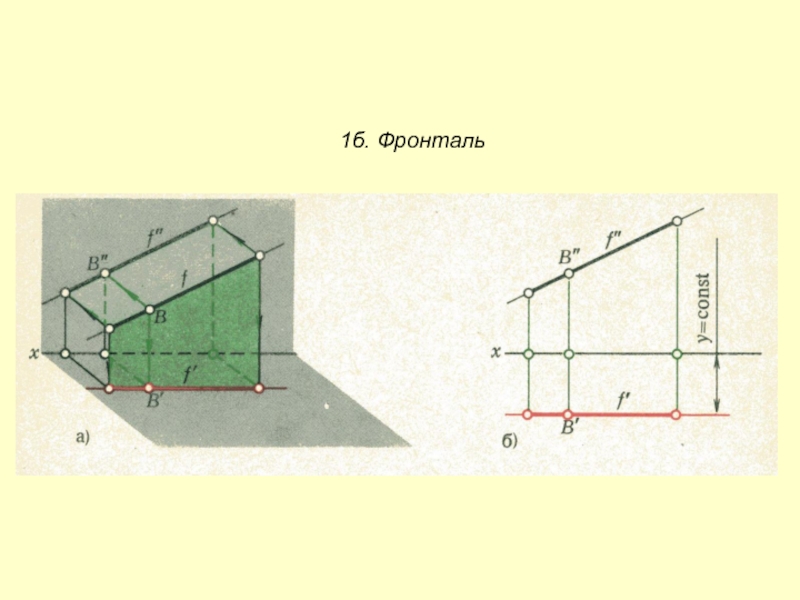
- 3. 1б. Фронталь
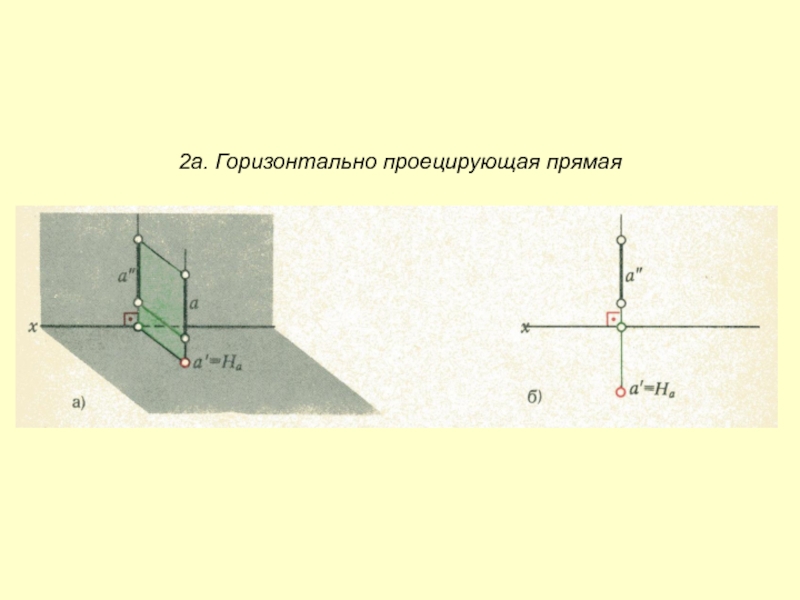
- 4. 2а. Горизонтально проецирующая прямая
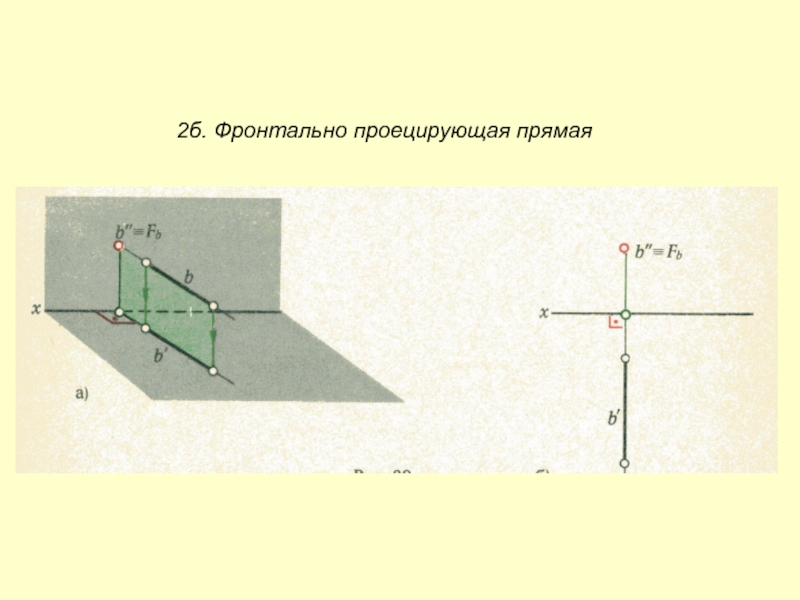
- 5. 2б. Фронтально проецирующая прямая
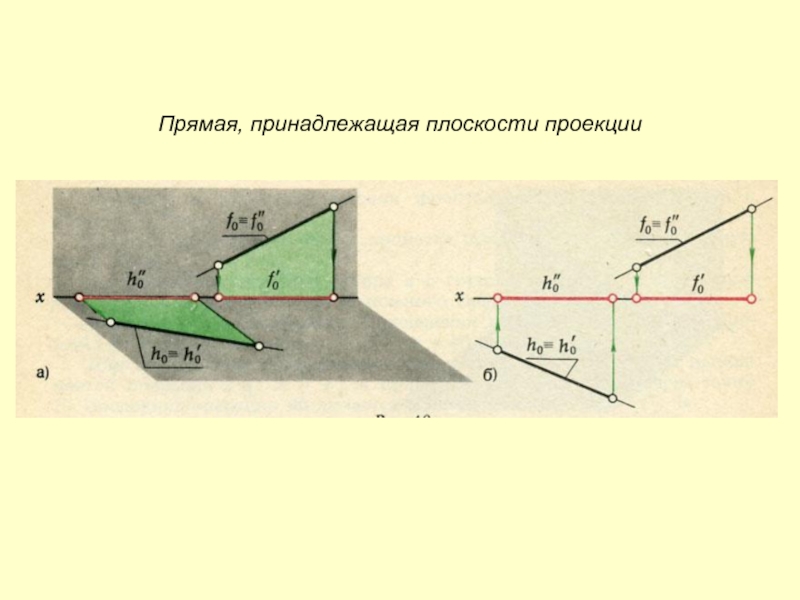
- 6. Прямая, принадлежащая плоскости проекции
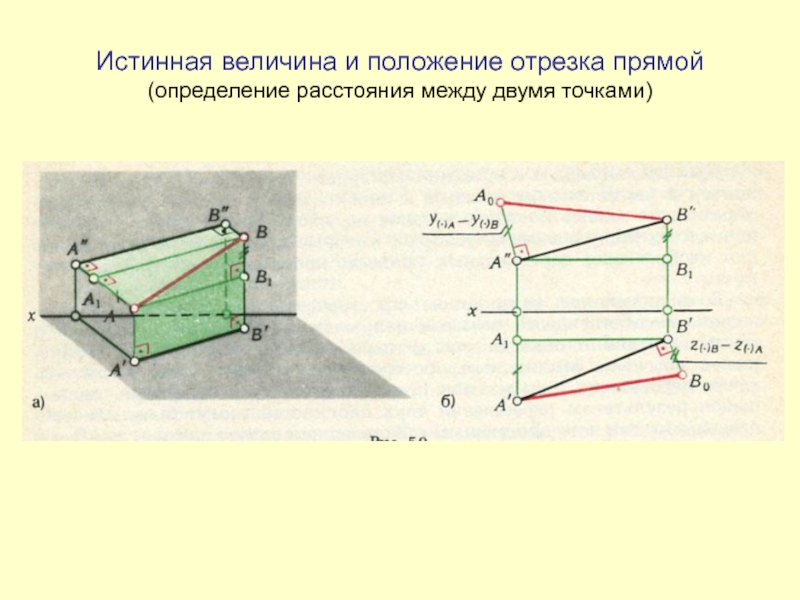
- 7. Истинная величина и положение отрезка прямой (определение расстояния между двумя точками)
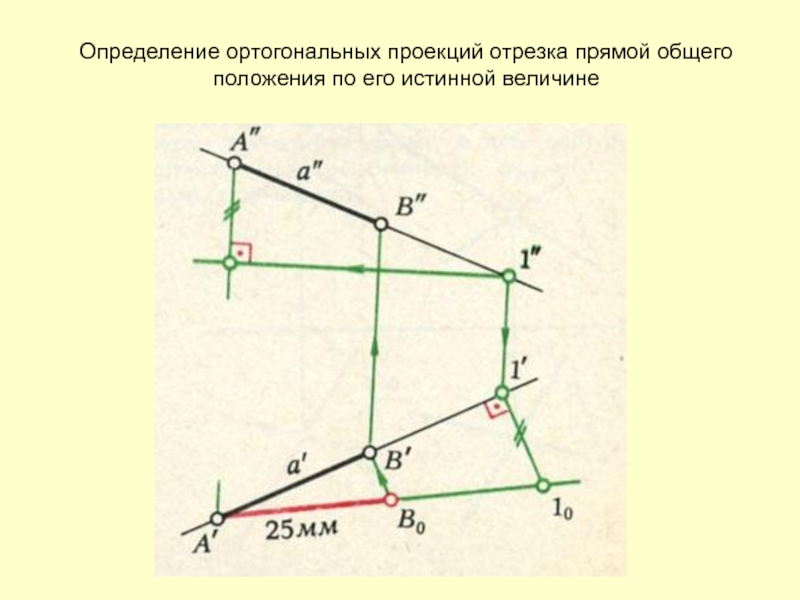
- 8. Определение ортогональных проекций отрезка прямой общего положения по его истинной величине
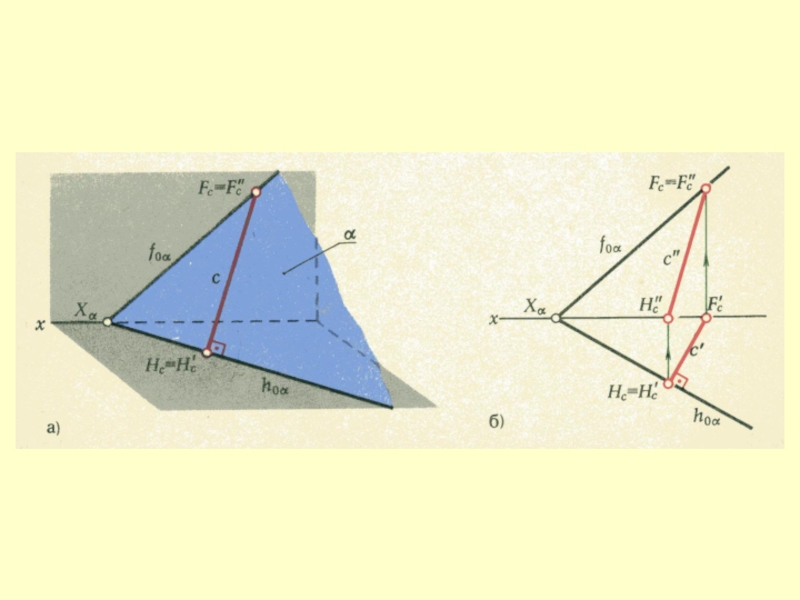
- 9. Ортогональные проекции плоскости
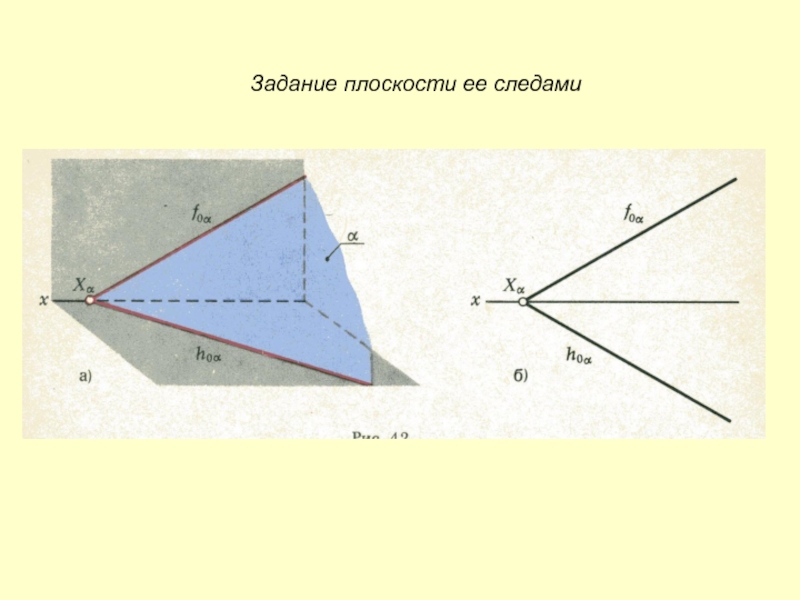
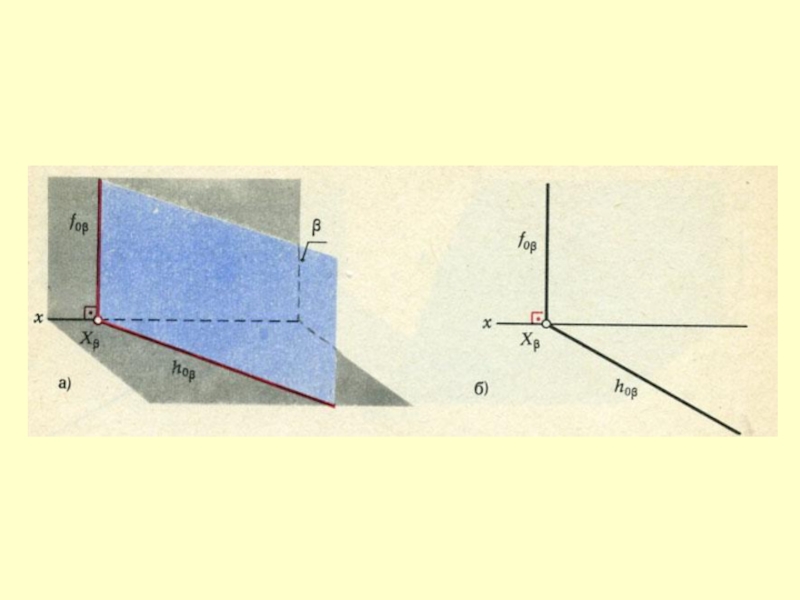
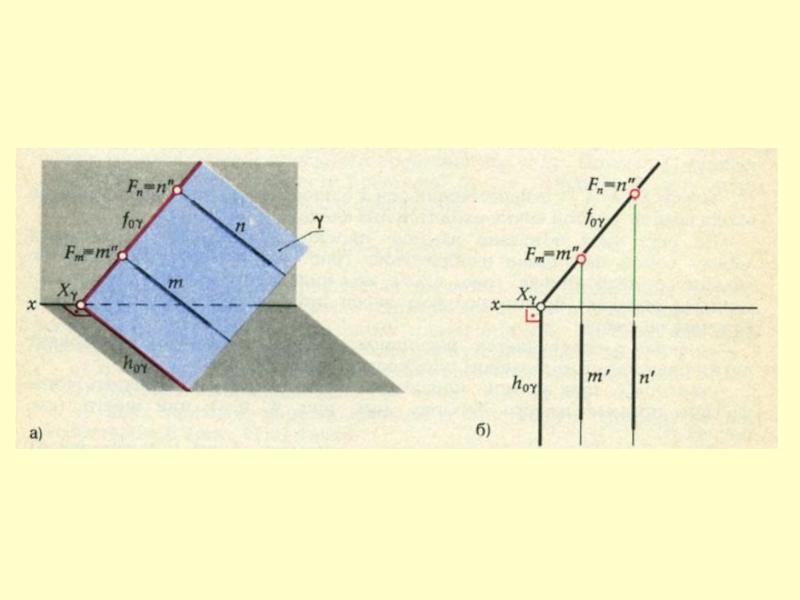
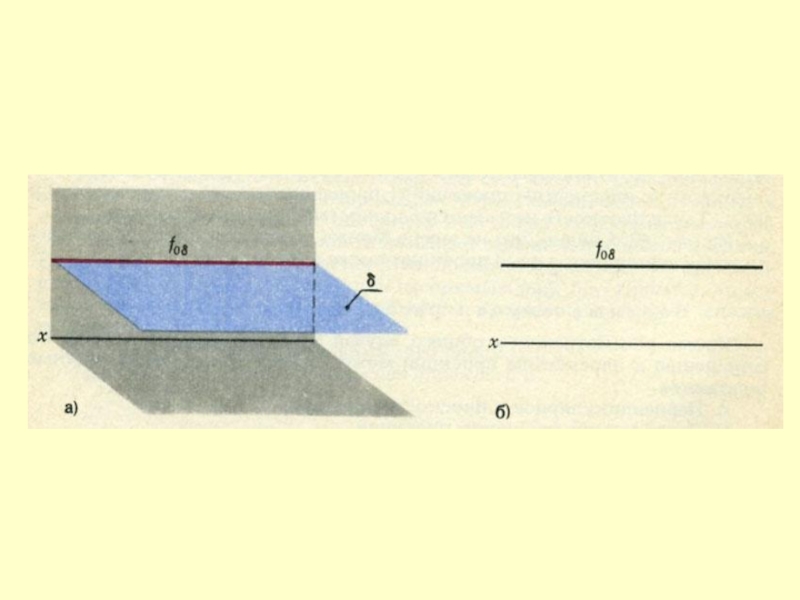
- 10. Задание плоскости ее следами
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
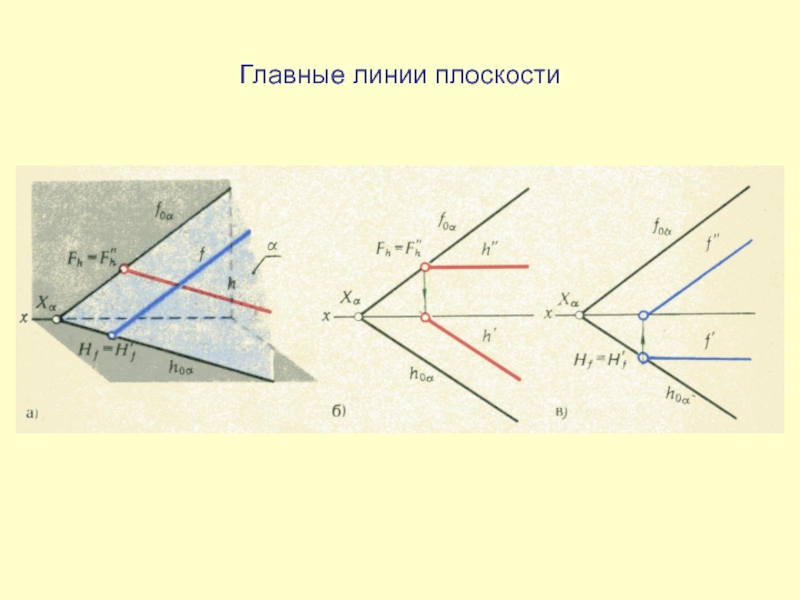
- 15. Главные линии плоскости
- 16. Слайд 16
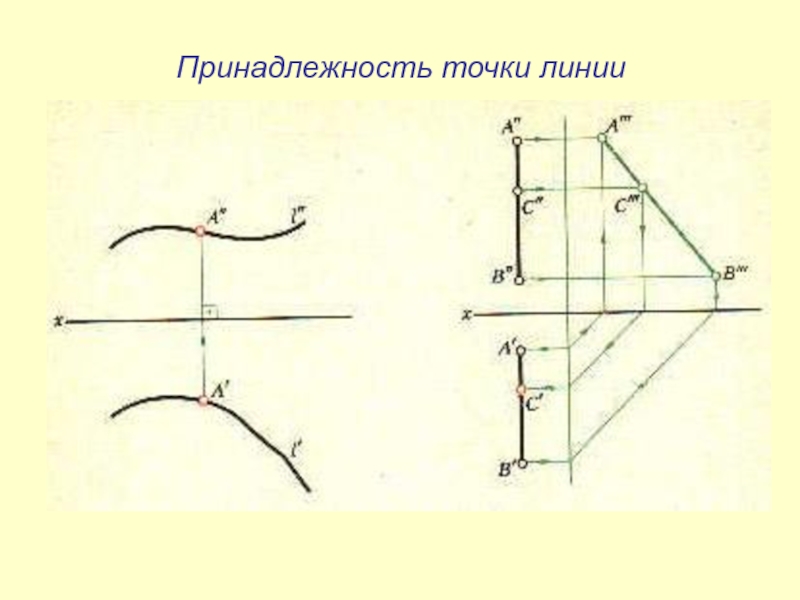
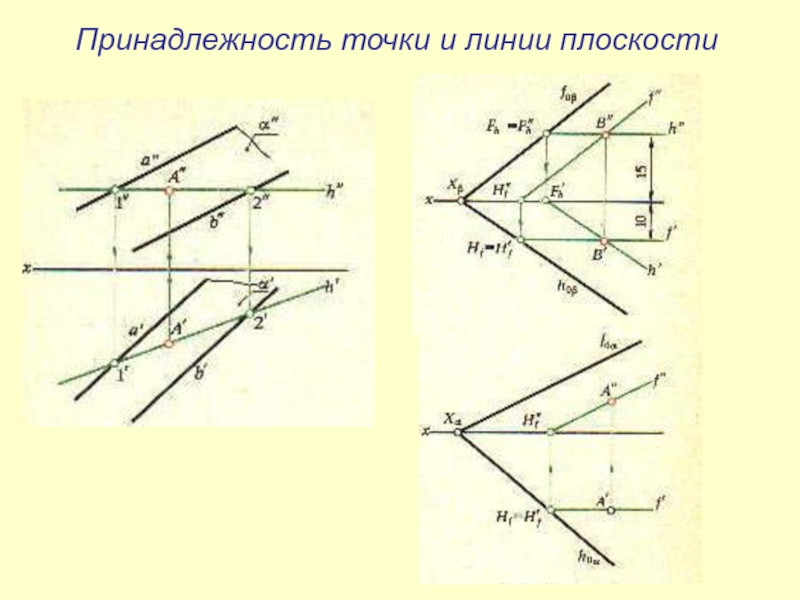
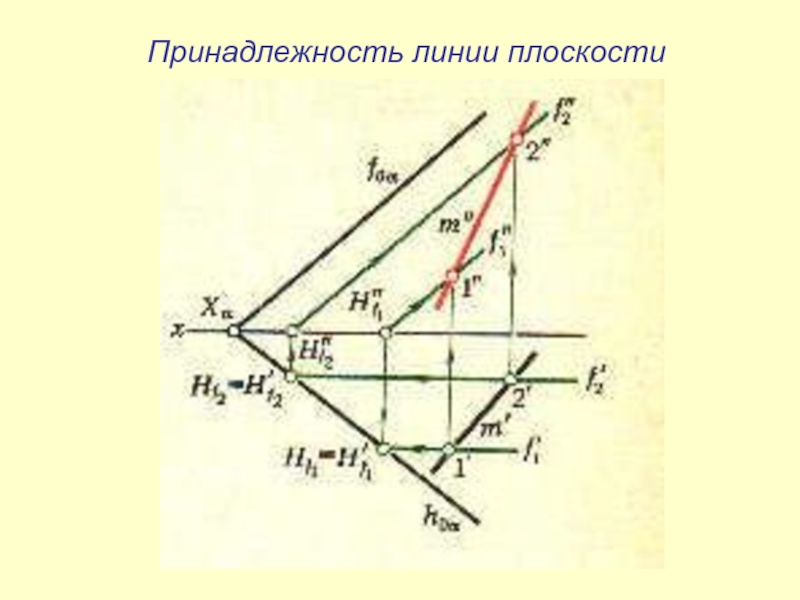
- 17. Принадлежность точки линии, точки плоскости и линии плоскостиПринадлежность точки линии2. Принадлежность точки плоскости3. Принадлежность линии плоскости
- 18. Принадлежность точки линии
- 19. Принадлежность точки и линии плоскости
- 20. Принадлежность линии плоскости
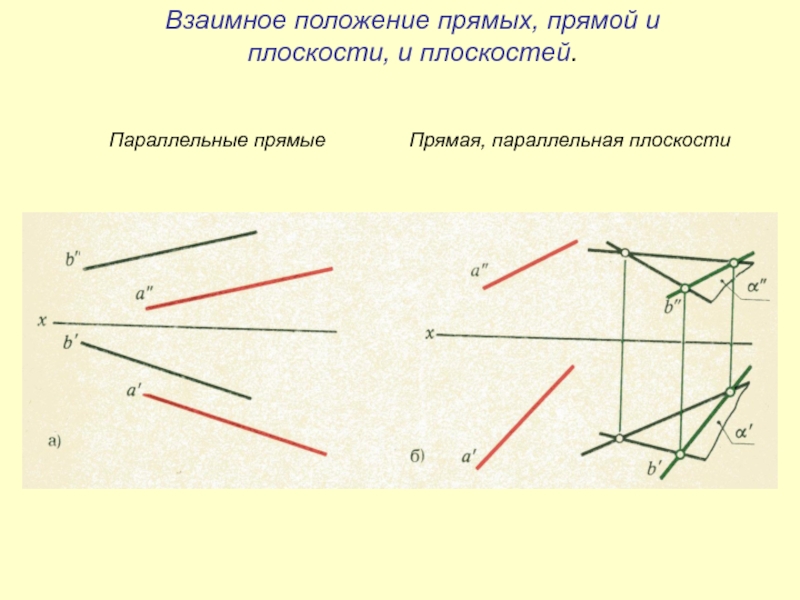
- 21. Взаимное положение прямых, прямой и плоскости, и плоскостей. Параллельные прямыеПрямая, параллельная плоскости
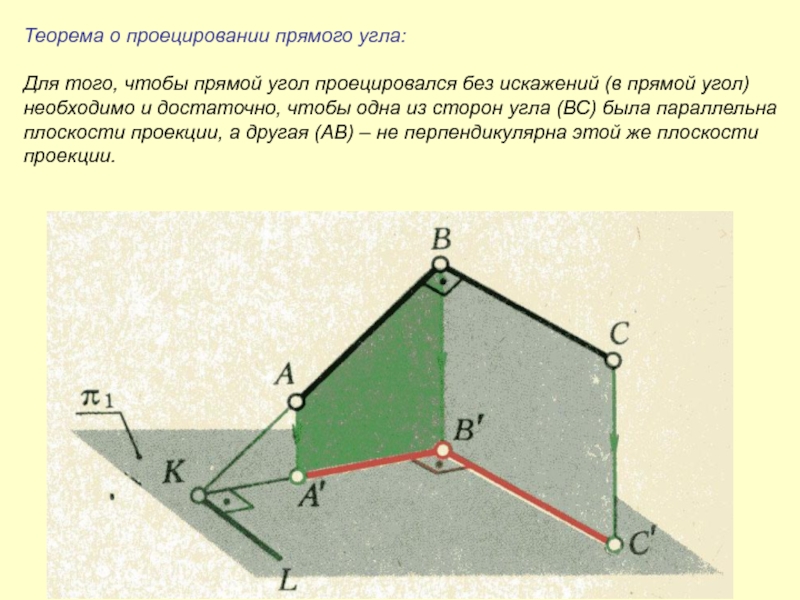
- 22. Теорема о проецировании прямого угла:Для того, чтобы
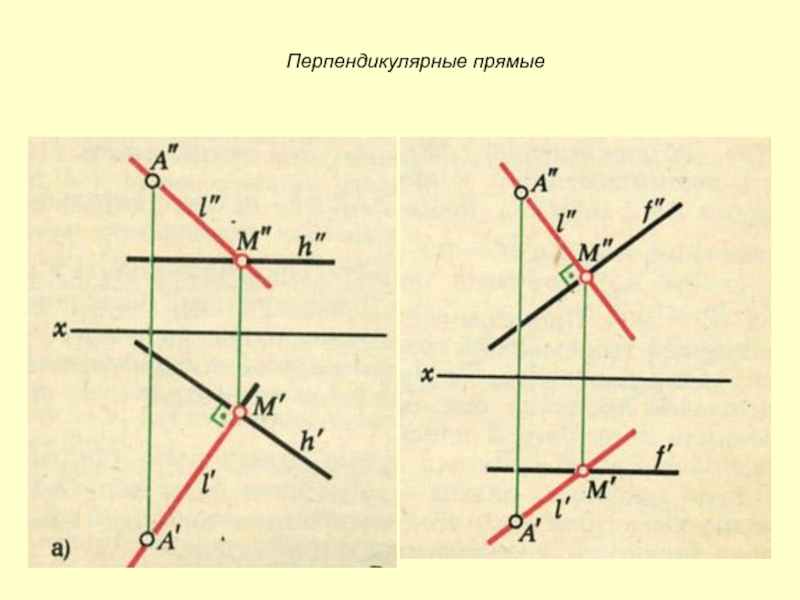
- 23. Перпендикулярные прямые
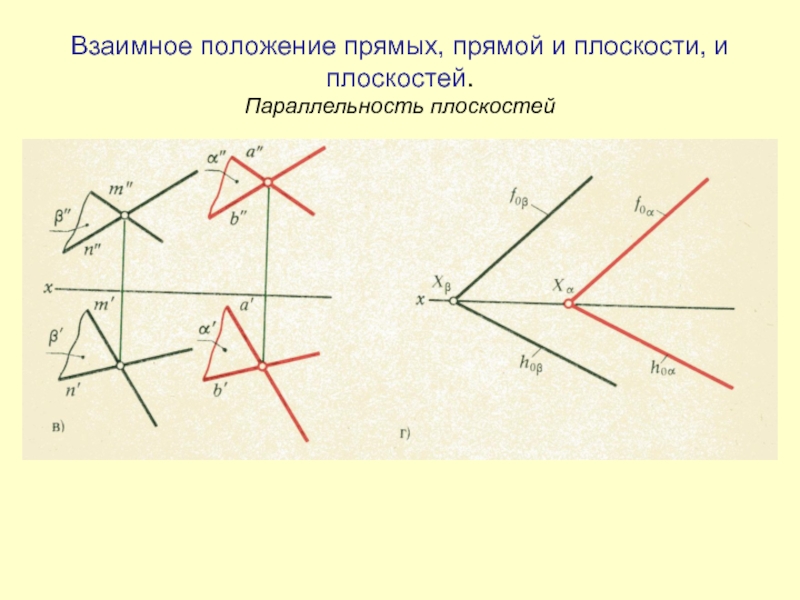
- 24. Взаимное положение прямых, прямой и плоскости, и плоскостей. Параллельность плоскостей
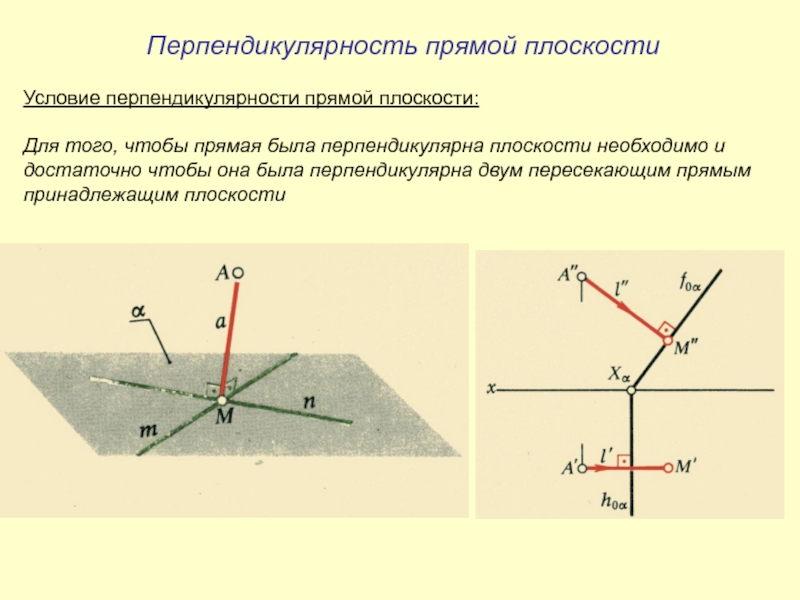
- 25. Перпендикулярность прямой плоскостиУсловие перпендикулярности прямой плоскости:Для того,
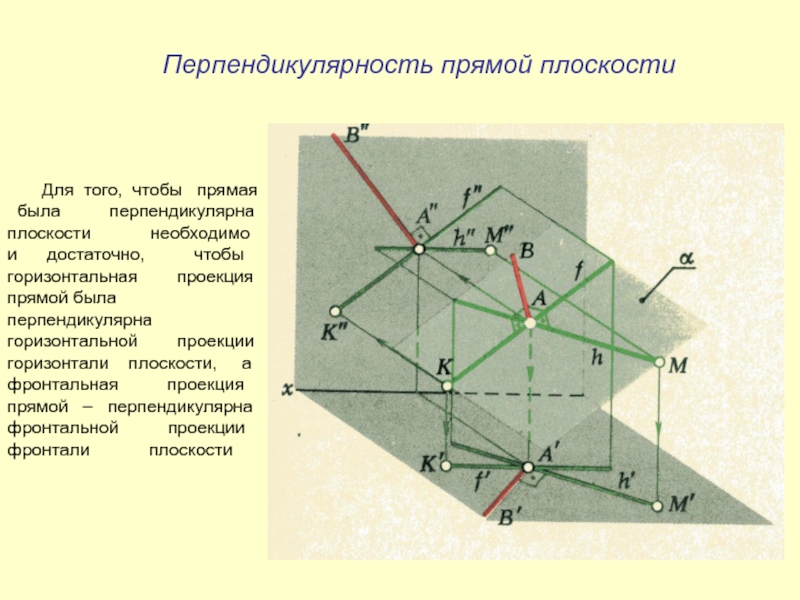
- 26. Перпендикулярность прямой плоскости Для
- 27. Перпендикулярность прямой плоскости
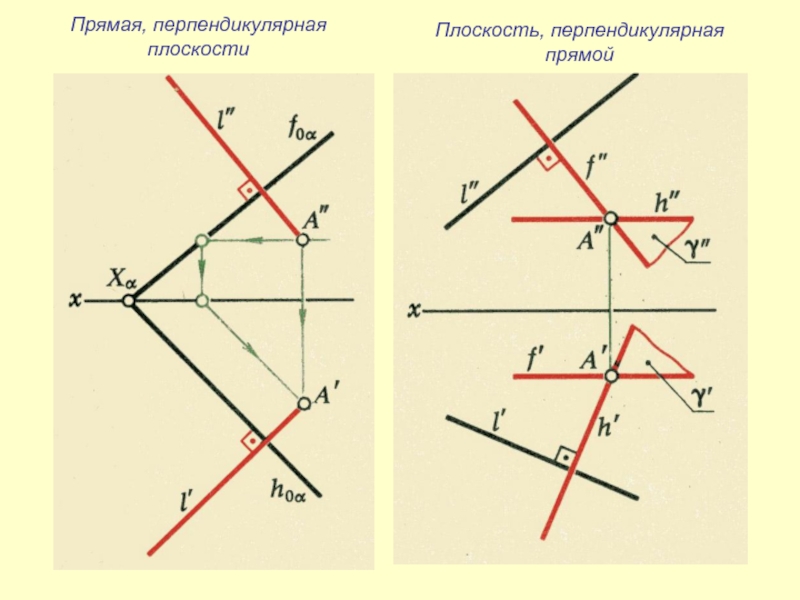
- 28. Прямая, перпендикулярнаяплоскостиПлоскость, перпендикулярнаяпрямой
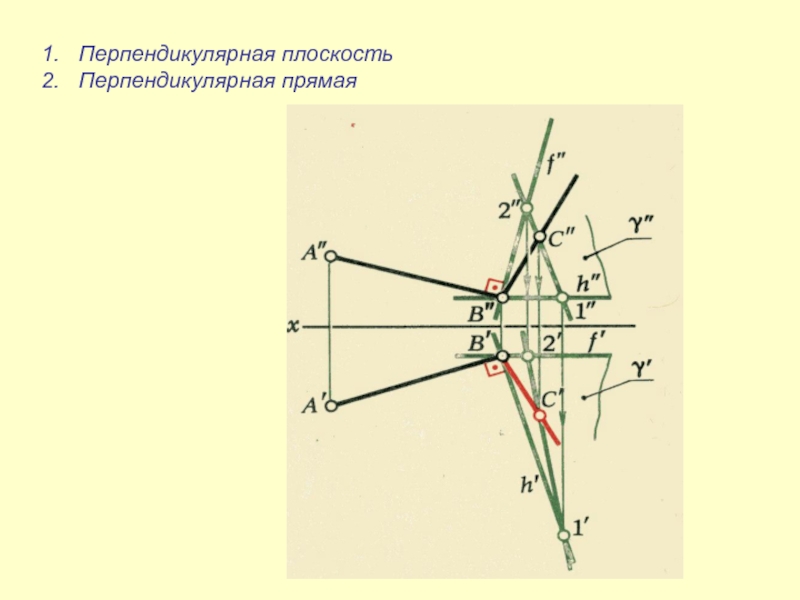
- 29. Перпендикулярная плоскостьПерпендикулярная прямая
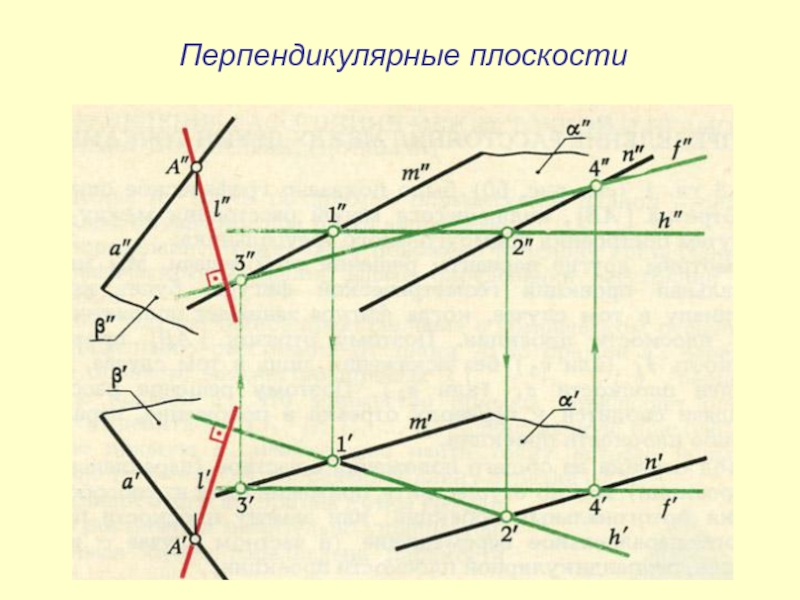
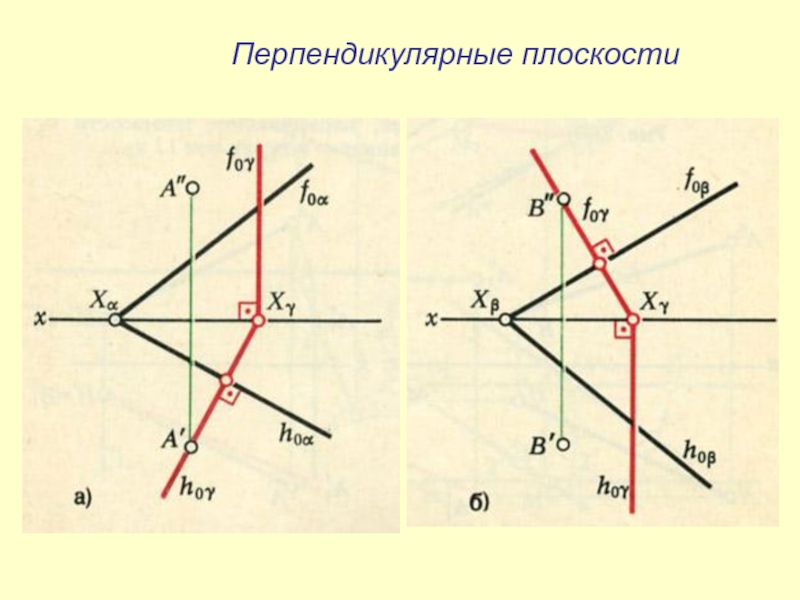
- 30. Перпендикулярные плоскости
- 31. Перпендикулярные плоскости
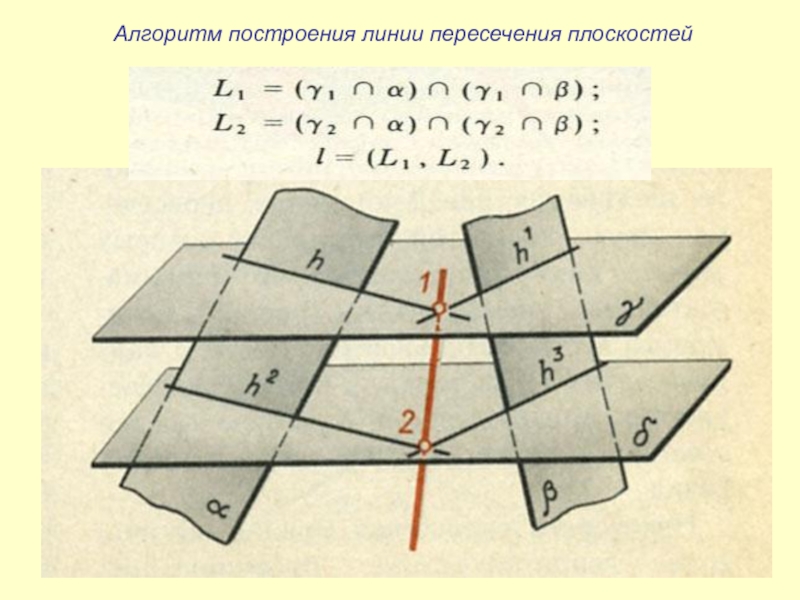
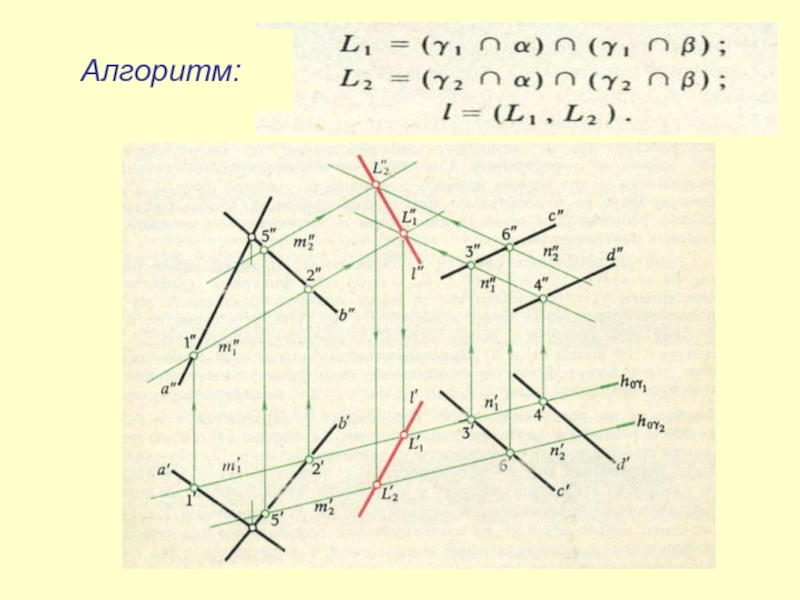
- 32. Алгоритм построения линии пересечения плоскостей
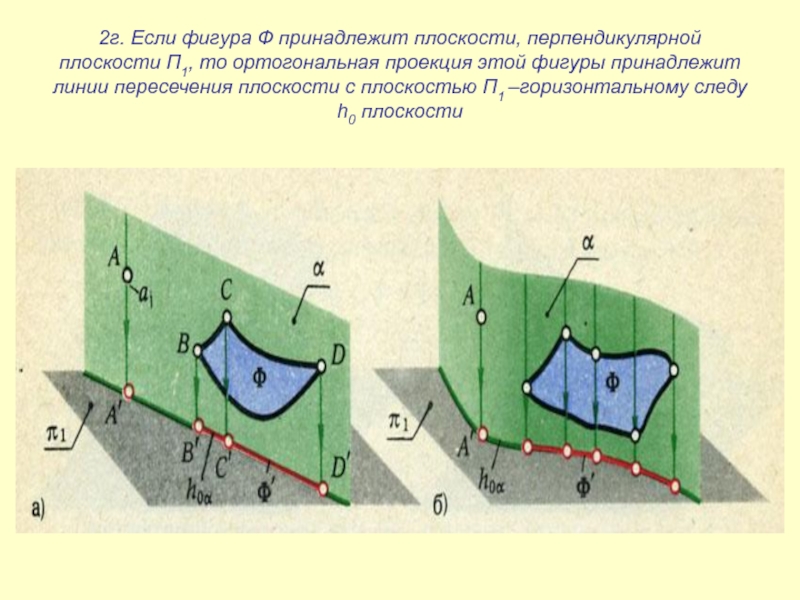
- 33. 2г. Если фигура Ф принадлежит плоскости, перпендикулярной
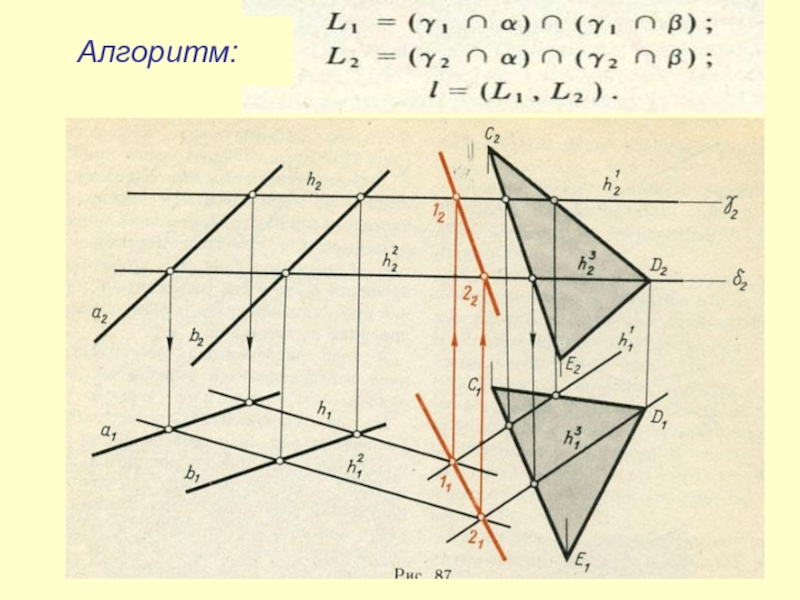
- 34. Алгоритм:
- 35. Алгоритм:
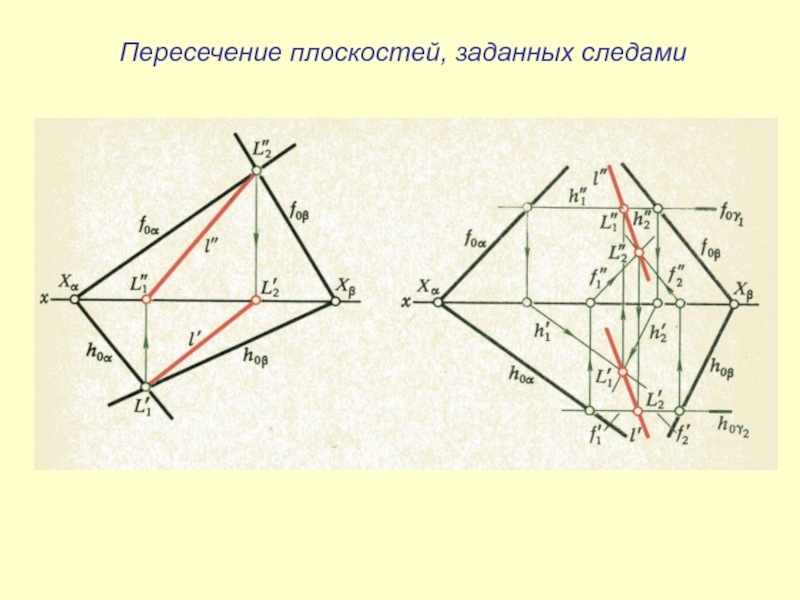
- 36. Пересечение плоскостей, заданных следами
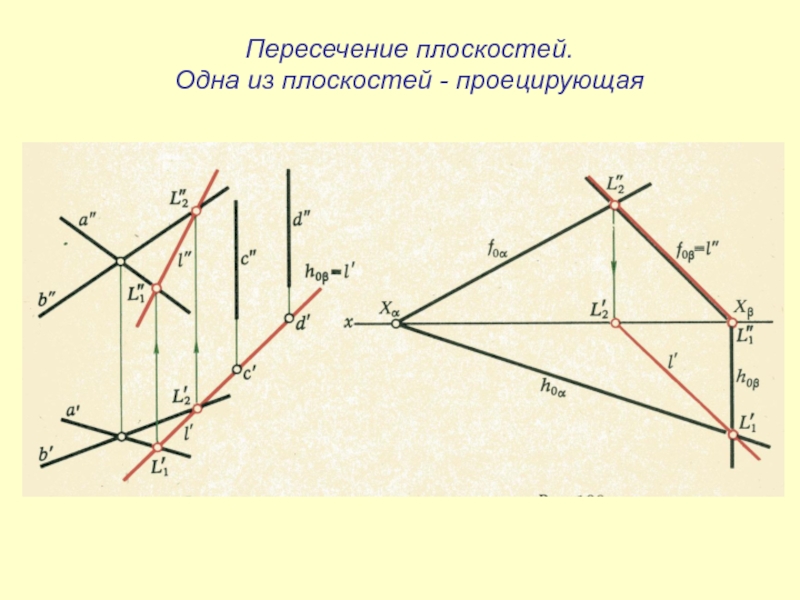
- 37. Пересечение плоскостей.Одна из плоскостей - проецирующая
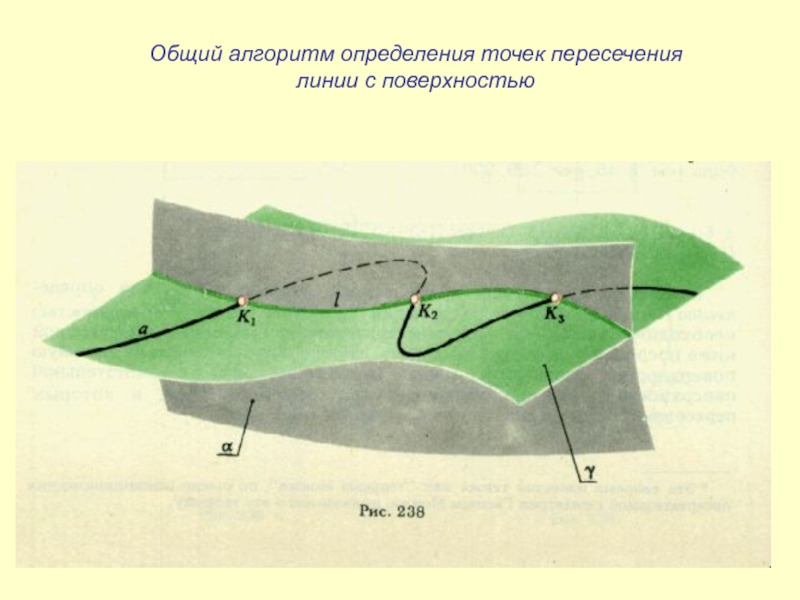
- 38. Общий алгоритм определения точек пересечения линии с поверхностью
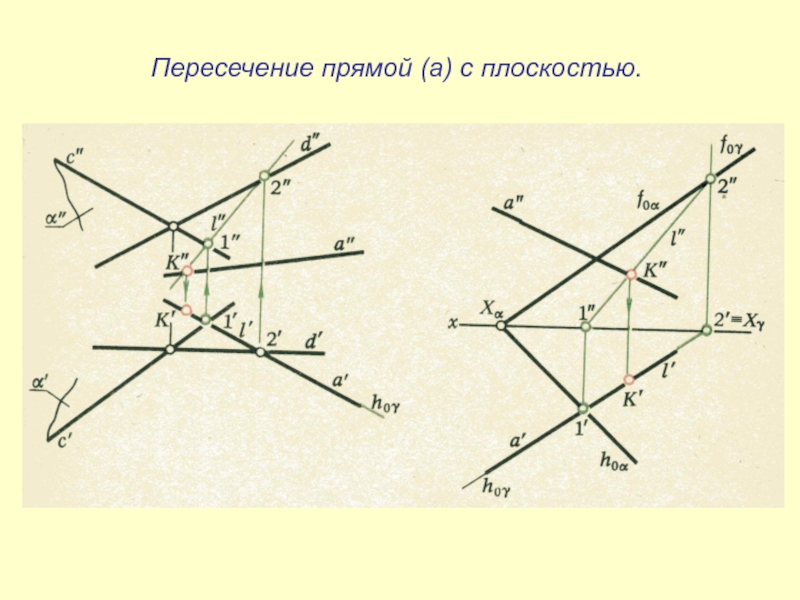
- 39. Пересечение прямой (а) с плоскостью.
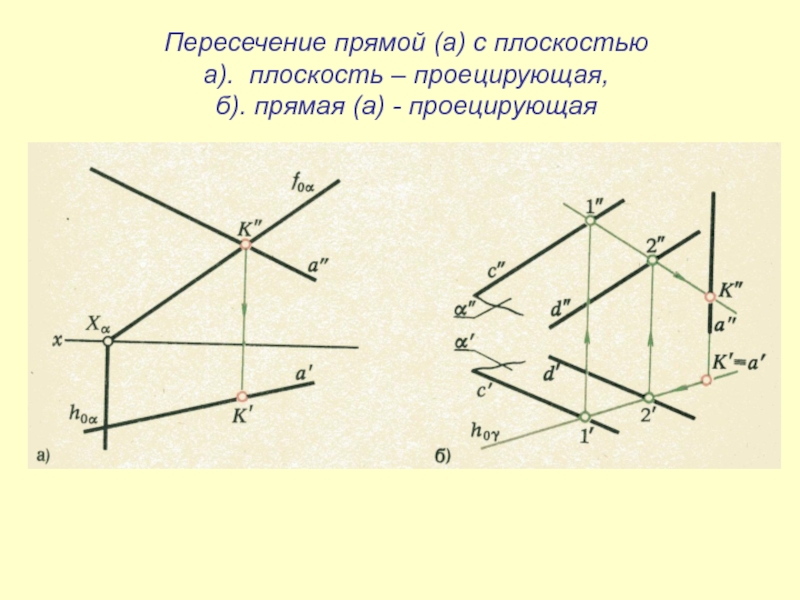
- 40. Пересечение прямой (а) с плоскостьюа). плоскость – проецирующая, б). прямая (а) - проецирующая
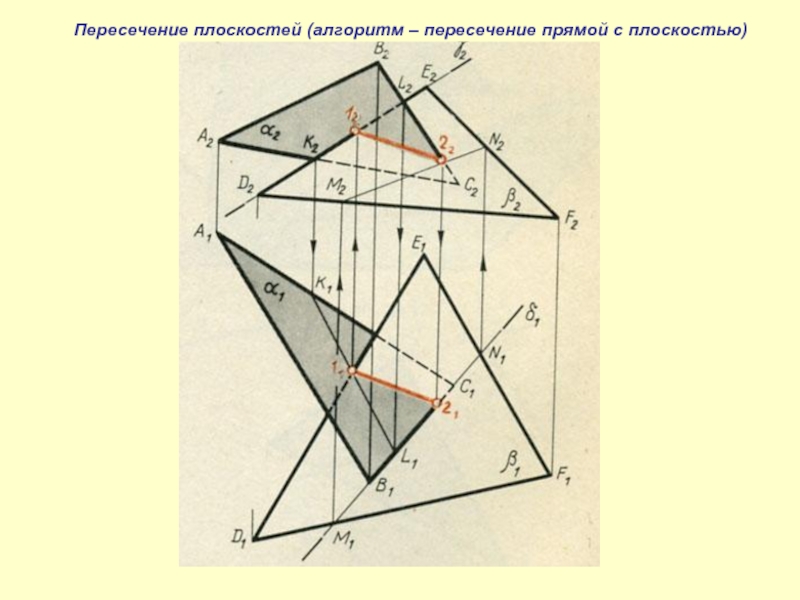
- 41. Пересечение плоскостей (алгоритм – пересечение прямой с плоскостью)
- 42. Скачать презентанцию
Прямые частного положения. 1. Прямые уровня (прямые параллельные какой-либо плоскости проекции): горизонталь, фронталь, профильная прямая. 2. Проецирующие прямые 1а. Горизонталь
Слайды и текст этой презентации
Слайд 1Ортогональные проекции прямой (Инвариантное свойство 1а: ортогональные проекции прямой, не перпендикулярные
плоскости проекции, есть прямые)
Слайд 2Прямые частного положения. 1. Прямые уровня (прямые параллельные какой-либо плоскости
проекции): горизонталь, фронталь, профильная прямая.
2. Проецирующие прямые
1а. Горизонталь
Слайд 17Принадлежность точки линии, точки плоскости и линии
плоскости
Принадлежность точки линии
2.
Принадлежность точки плоскости
3. Принадлежность линии плоскости
Слайд 21Взаимное положение прямых, прямой и плоскости, и плоскостей.
Параллельные прямые
Прямая, параллельная
плоскости
Слайд 22Теорема о проецировании прямого угла:
Для того, чтобы прямой угол проецировался
без искажений (в прямой угол)
необходимо и достаточно, чтобы одна
из сторон угла (ВС) была параллельнаплоскости проекции, а другая (АВ) – не перпендикулярна этой же плоскости
проекции.
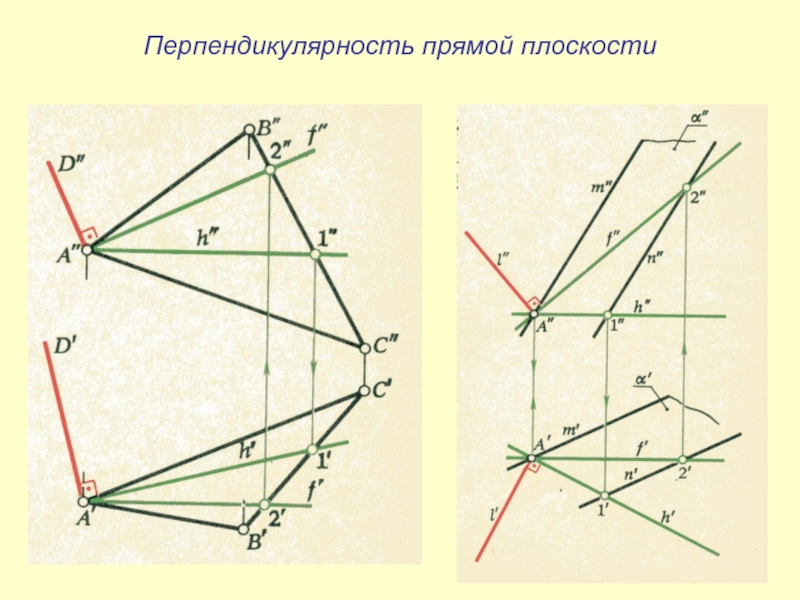
Слайд 25Перпендикулярность прямой плоскости
Условие перпендикулярности прямой плоскости:
Для того, чтобы прямая была
перпендикулярна плоскости необходимо и
достаточно чтобы она была перпендикулярна двум пересекающим
прямым принадлежащим плоскости
Слайд 26Перпендикулярность прямой плоскости
Для того, чтобы
прямая
была перпендикулярна
плоскости
необходимои достаточно, чтобы
горизонтальная проекция
прямой была перпендикулярна
горизонтальной проекции
горизонтали плоскости, а
фронтальная проекция
прямой – перпендикулярна
фронтальной проекции
фронтали плоскости
Слайд 332г. Если фигура Ф принадлежит плоскости, перпендикулярной плоскости П1, то
ортогональная проекция этой фигуры принадлежит линии пересечения плоскости с плоскостью
П1 –горизонтальному следу h0 плоскости
Слайд 40Пересечение прямой (а) с плоскостью
а). плоскость – проецирующая,
б). прямая
(а) - проецирующая
