ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Содержание

1. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
2. Основные уравнения электромагнитного поля, называемые уравнениями Максвелла,
3. Закон полного тока устанавливает количественное соотношение между напряженностью магнитного поля H и током I
4. Первое уравнение Максвелла Согласно закону полного тока
5. Закон электромагнитной индукции (закон Фарадея) устанавливает соотношение
6. Второе уравнение Максвелла В соответствии с законом
7. Уравнения Максвелла в дифференциальной форме Эти уравнения
8. Основные уравнения электромагнитного поля для гармонических колебаний
9. Уравнения Максвелла для «чистых» проводниковПри рассмотрении процессов
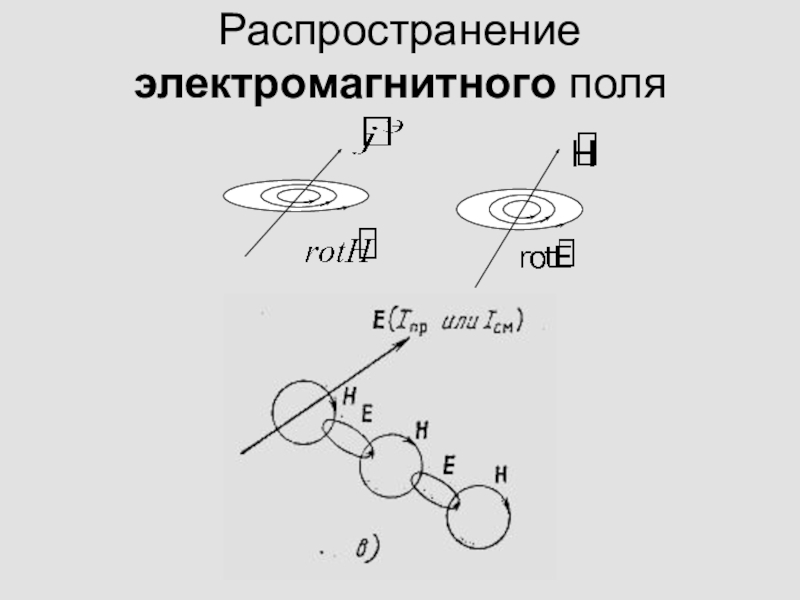
10. Распространение электромагнитного поля
11. Уравнения Максвелла для диэлектриков и световодовВ диэлектрических
12. Волновые уравнения в векторной форме. Уравнения Максвелла
13. к – коэффициент распространения в среде (комплексная величина: α – коэффициент затухания; β – коэффициент фазы)
14. Уравнения Максвелла в цилиндрической системе координат для
15. После дифференцирования Нr по  и H
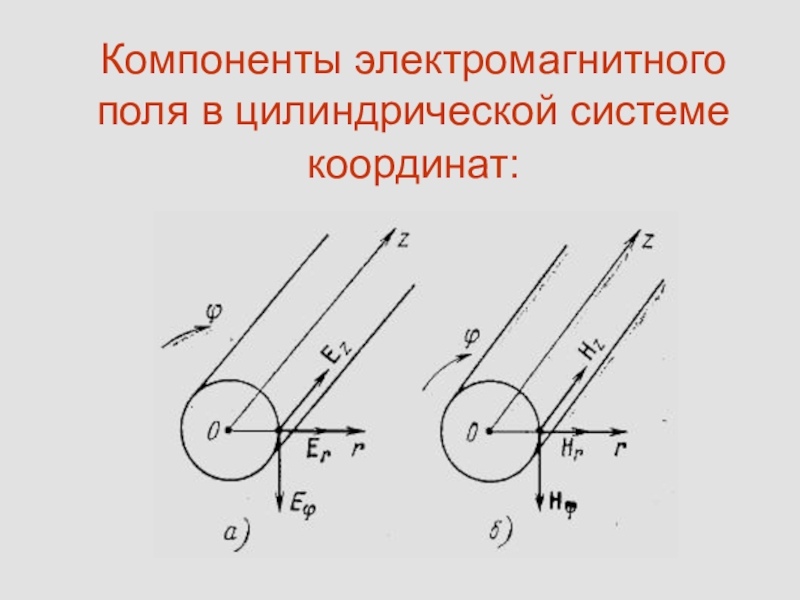
16. Компоненты электромагнитного поля в цилиндрической системе координат:
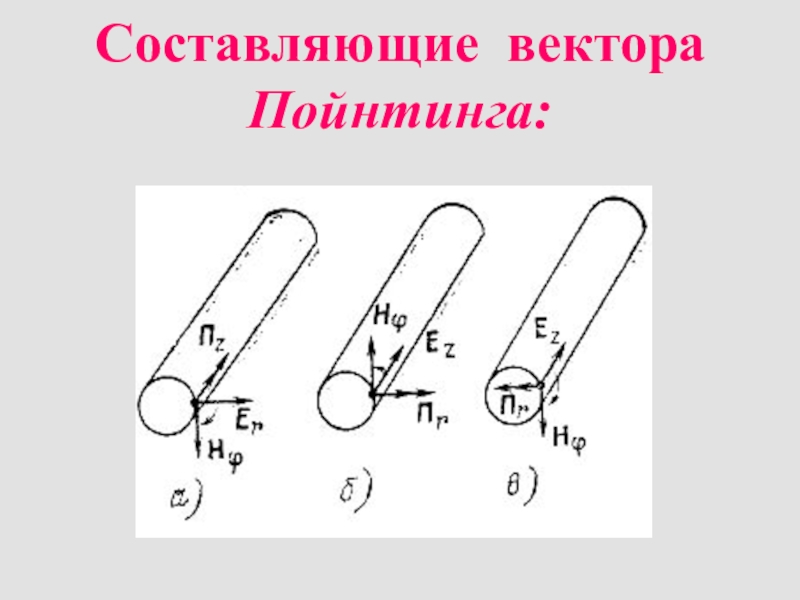
17. Составляющие вектора Пойнтинга:
18. Запас электромагнитной энергии в объеме V
19. Теорема Умова-ПойнтингаТеорема Умова - Пойнтинга характеризует баланс
20. Вектор Умова-Пойнтинга Количество энергии, распространяющейся в единицу
21. Скачать презентанцию

Основные уравнения электромагнитного поля, называемые уравнениями Максвелла, обобщают два основных закона электротехники: закон полного тока и закон электромагнитной индукции.

Главная
Разное
ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Слайды и текст этой презентации

Слайд 1ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Уравнения МАКСВЕЛЛА

Слайд 2Основные уравнения электромагнитного поля, называемые уравнениями Максвелла, обобщают два основных

закона электротехники: закон полного тока и закон электромагнитной индукции.

Основные уравнения электромагнитного поля, называемые уравнениями Максвелла, обобщают два основных закона электротехники: закон полного

Слайд 3Закон полного тока
устанавливает количественное соотношение между напряженностью
магнитного поля

H и током I

Слайд 4Первое уравнение Максвелла
Согласно закону полного тока линейный интеграл напряженности

магнитного поля по любому замкнутому контуру равен полному току, протекающему

через поверхность, ограниченную этим контуром. Полный ток складывается из токов смещения и токов проводимости:

Первое уравнение Максвелла Согласно закону полного тока линейный интеграл напряженности магнитного поля по любому замкнутому контуру равен

Слайд 5Закон электромагнитной индукции (закон Фарадея)
устанавливает соотношение между напряженностью
электрического

поля Е и магнитным потоком Ф

Закон электромагнитной индукции (закон Фарадея) устанавливает соотношение между напряженностью электрического поля Е и магнитным потоком Ф

Слайд 6Второе уравнение Максвелла
В соответствии с законом электромагнитной индукции, открытым

Фарадеем, электродвижущая сила, возникающая в контуре при изменении магнитного потока

Ф, пронизывающего поверхность, ограниченную контуром, равна скорости изменения этого потока со знаком минус:

Второе уравнение Максвелла В соответствии с законом электромагнитной индукции, открытым Фарадеем, электродвижущая сила, возникающая в контуре при

Слайд 7Уравнения Максвелла в дифференциальной форме
Эти уравнения часто используются для решения

практических задач
К уравнениям Максвелла также относят еще два вспомогательных

уравнения:

Слайд 8Основные уравнения электромагнитного поля для гармонических колебаний в комплексной форме
где

– плотность тока проводимости (в

металлических массах);
- плотность тока смещения (в диэлектрике)

Основные уравнения электромагнитного поля для гармонических колебаний в комплексной формегде –

Слайд 9Уравнения Максвелла для «чистых» проводников
При рассмотрении процессов в проводниках током

смещения можно пренебречь и расчетные формулы приобретут вид

Уравнения Максвелла для «чистых» проводниковПри рассмотрении процессов в проводниках током смещения можно пренебречь и расчетные формулы приобретут

Слайд 10Распространение электромагнитного поля

Слайд 11Уравнения Максвелла для диэлектриков и световодов
В диэлектрических направляющих системах (диэлектрические

волноводы, световоды), а также в атмосфере преобладают токи смещения и

для их анализа пользуются следующими уравнениями

Уравнения Максвелла для диэлектриков и световодовВ диэлектрических направляющих системах (диэлектрические волноводы, световоды), а также в атмосфере преобладают

Слайд 12 Волновые уравнения в векторной форме.
Уравнения Максвелла образуют систему взаимосвязанных

дифференциальных уравнений первого порядка, решение которых с учетом граничных условий

в некотором случае весьма затруднительно. Для преодоления указанных трудностей переходят к более простой форме записи уравнений. Для её получения применяют к обеим частям уравнения операцию rot.
Отсюда получают:

Волновые уравнения в векторной форме. Уравнения Максвелла образуют систему взаимосвязанных дифференциальных уравнений первого порядка, решение которых с

Слайд 13к – коэффициент распространения в среде (комплексная величина: α –

коэффициент затухания; β – коэффициент фазы)

Слайд 14Уравнения Максвелла в цилиндрической системе координат для проводников
Так как направляющие

системы имеют цилиндрическую конструкцию, то наиболее часто записывают уравнения Максвелла

в цилиндрической системе координат (оси z, r, ), при этом ось z совмещают с осью направляющей системы

Уравнения Максвелла в цилиндрической системе координат для проводниковТак как направляющие системы имеют цилиндрическую конструкцию, то наиболее часто

Слайд 15После дифференцирования Нr по  и H по r и

подстановки полученных производных в предыдущие уравнения получим

Слайд 16Компоненты электромагнитного поля в цилиндрической системе координат:

Слайд 17Составляющие вектора Пойнтинга:

Слайд 18Запас электромагнитной энергии в объеме V

Слайд 19Теорема Умова-Пойнтинга
Теорема Умова - Пойнтинга характеризует баланс энергии электромагнитного поля.

Левая часть этого выражения характеризует расход электромагнитной энергии за единицу

времени, правая часть показывает, на что расходуется за единицу времени заключенная в объеме энергия.

Теорема Умова-ПойнтингаТеорема Умова - Пойнтинга характеризует баланс энергии электромагнитного поля. Левая часть этого выражения характеризует расход электромагнитной

Слайд 20Вектор Умова-Пойнтинга
Количество энергии, распространяющейся в единицу времени через единичную

площадку, перпендикулярную направлению потока энергии, выражается векторной величиной называемой вектором

Умова-Пойнтинга (чаще вектором Пойнтинга)

Вектор Умова-Пойнтинга Количество энергии, распространяющейся в единицу времени через единичную площадку, перпендикулярную направлению потока энергии, выражается векторной

Скачать презентацию

Разделы презентаций

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Содержание

Слайды и текст этой презентации

Слайд 1ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ Уравнения МАКСВЕЛЛА

Слайд 2Основные уравнения электромагнитного поля, называемые уравнениями Максвелла, обобщают два основных

закона электротехники: закон полного тока и закон электромагнитной индукции.

Слайд 3Закон полного тока устанавливает количественное соотношение между напряженностью магнитного поля

H и током I

Слайд 4Первое уравнение Максвелла Согласно закону полного тока линейный интеграл напряженности

магнитного поля по любому замкнутому контуру равен полному току, протекающему

Слайд 5Закон электромагнитной индукции (закон Фарадея) устанавливает соотношение между напряженностью электрического