Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные понятия теории графов
Содержание
- 1. Основные понятия теории графов
- 2. Основные понятия Граф G=(V,E) состоит из двух множеств:
- 3. Основные понятия Вершины vi и vj, определяющие ребро
- 4. Основные понятия Изолированная вершина не инцидентна ни одному
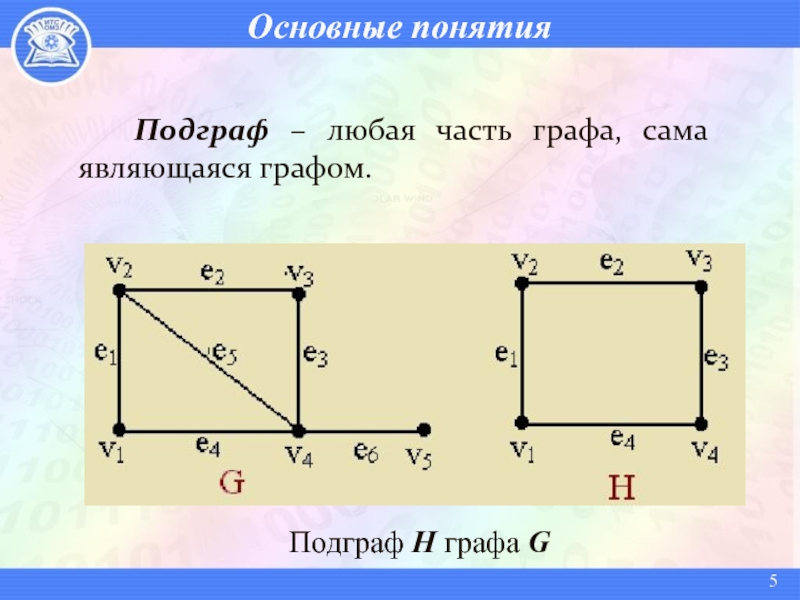
- 5. Основные понятия Подграф – любая часть графа, сама являющаяся графом.Подграф H графа G
- 6. Виды графов Граф G=(V,E) называется простым, если он
- 7. Виды графов Ноль-граф - граф, множество ребер которого пусто. Граф G с кратными ребрами называется мультиграф.
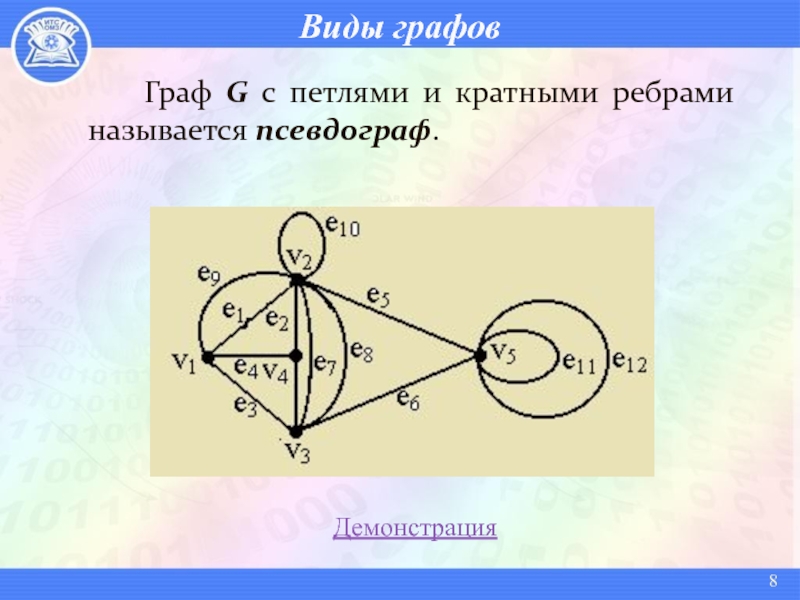
- 8. Виды графов Граф G с петлями и кратными ребрами называется псевдограф.Демонстрация
- 9. Неориентированный граф Граф G, рёбра которого не имеют определённого направления, называется неориентированным.
- 10. Ориентированный граф Граф G, имеющий определённое направление, называется ориентированным графом или орграфом. Ребра, имеющие направление, называются дугами.Демонстрация
- 11. Способы задания графов1) Явное задание графа как
- 12. Способы задания графов2) Геометрический.
- 13. Способы задания графов3) Матрица смежности. Элементы Aij матрицы смежности A равны количеству ребер между рассматриваемыми вершинами.
- 14. Матрица смежности неорграфаДля неорграфа G, представленного на рисунке, матрица смежности имеет вид:
- 15. Матрица смежности орграфаДля орграфа G, представленного на рисунке, матрица смежности имеет вид:
- 16. Способы задания графов4) Матрица инцидентности. Матрица
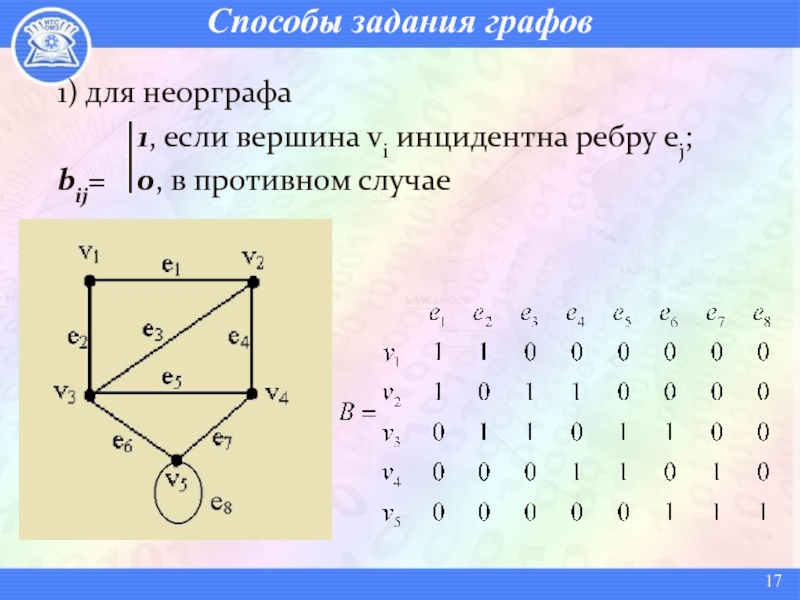
- 17. Способы задания графов1) для неорграфа 1, если вершина vi инцидентна ребру ej;bij= 0, в противном случае
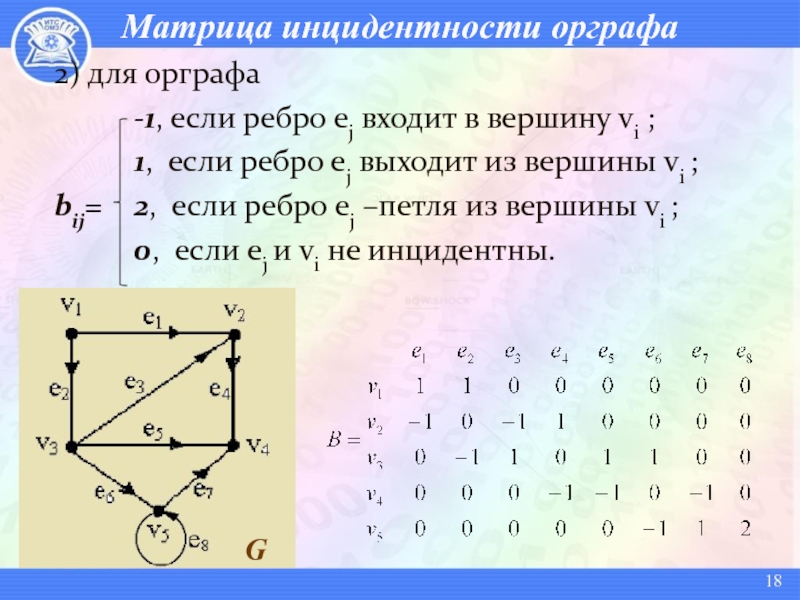
- 18. Матрица инцидентности орграфа2) для орграфа -1, если ребро
- 19. Маршрут Маршрут в графе G=(V,E) — конечная чередующееся
- 20. Маршрут Маршрут называется открытым, если его концевые вершины
- 21. Цепь Маршрут называется цепью, если все его ребра
- 22. Путь, цикл Открытая цепь называется путем, если все
- 23. Cвойства путей и циклов1. Степень каждой
- 24. Связность графов, компонента связности Две вершины vi и
- 25. Степень вершины Степенью deg(vj) вершины vj называется число
- 26. Сумма степеней вершин графа Утверждение («лемма о рукопожатиях») Сумма
- 27. Изоморфизм графов Два графа G1 и G2 изоморфны,
- 28. Пример изоморфных графовСоответствие вершин: v1↔v2’,v2↔v3’,v3↔v1’,v4↔v4’,v5↔v5’;Соответствие ребер: e1↔e1’, e3↔e2’,
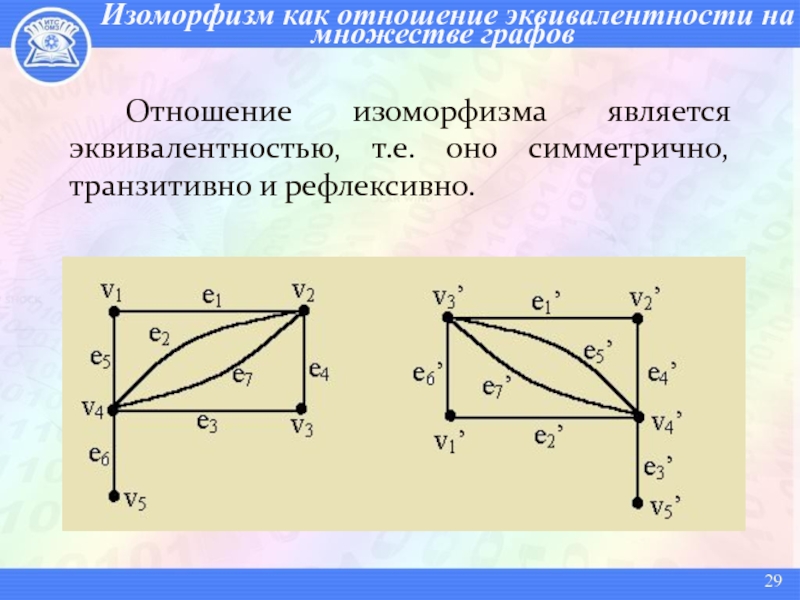
- 29. Изоморфизм как отношение эквивалентности на множестве графов Отношение
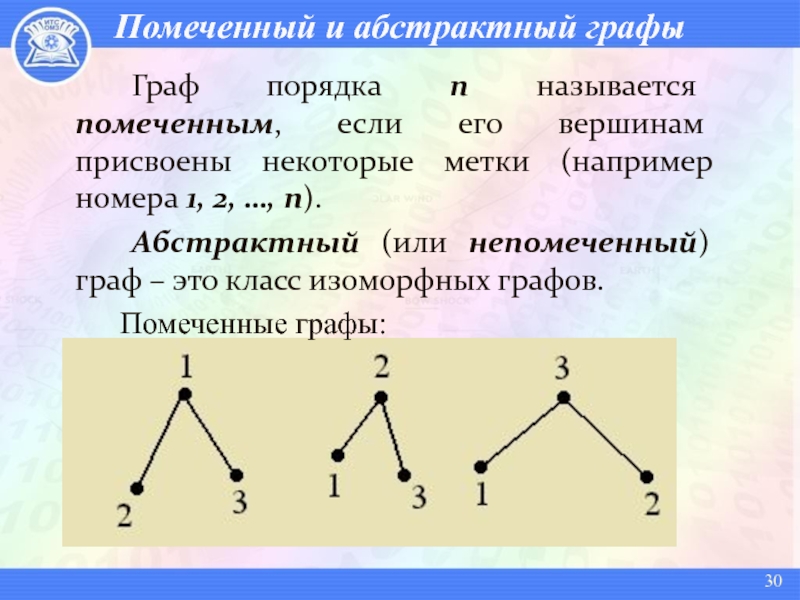
- 30. Помеченный и абстрактный графы Граф порядка n называется
- 31. Скачать презентанцию
Основные понятия Граф G=(V,E) состоит из двух множеств: конечного множества элементов, называемых вершинами, и конечного множества элементов, называемых ребрами.Граф G=(V, E) V={v1, v2, v3, v4, v5} ; E={e1, e2, e3, e4, e5,
Слайды и текст этой презентации
Слайд 1Основные понятия теории графов
ХНУРЭ, кафедра ПО ЭВМ, Тел. 7021-446, e-mail:
belous@kture.Kharkov.ua
Слайд 2Основные понятия
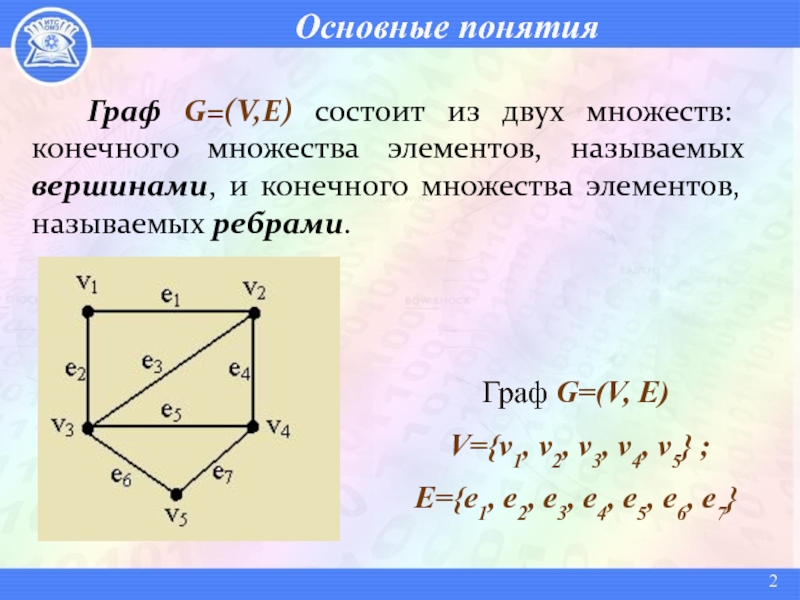
Граф G=(V,E) состоит из двух множеств: конечного множества элементов,
называемых вершинами, и конечного множества элементов, называемых ребрами.
Граф G=(V, E)
V={v1, v2, v3, v4, v5} ; E={e1, e2, e3, e4, e5, e6, e7}
Слайд 3Основные понятия
Вершины vi и vj, определяющие ребро ek, называются концевыми
вершинами ребра ek.
Ребра с одинаковыми концевыми
вершинами называются параллельными (e1,e4 ).Петля– замкнутое ребро(e5).
Ребро, принадлежащее вершине, называется инцидентным (ребро e1 инцидентно вершинам v1 и v2).
Слайд 4Основные понятия
Изолированная вершина не инцидентна ни одному ребру (v3).
Две вершины
смежны, если они являются концевыми вершинами некоторого ребра (v1, v4).
Если два ребра имеют общую концевую вершину, они называются смежными (e1, e2).
G
Демонстрация
Слайд 6Виды графов
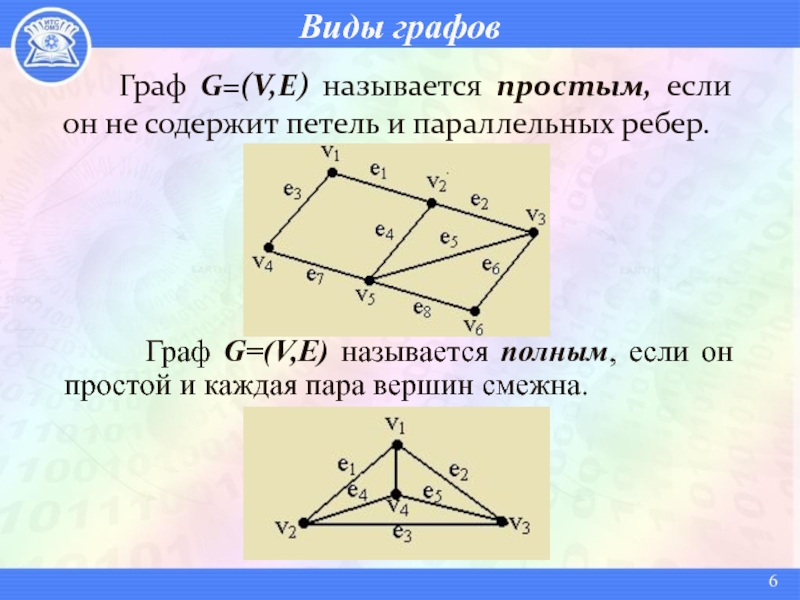
Граф G=(V,E) называется простым, если он не содержит петель
и параллельных ребер.
Граф G=(V,E) называется полным,
если он простой и каждая пара вершин смежна. 
Слайд 7Виды графов
Ноль-граф - граф, множество ребер которого пусто.
Граф G с
кратными ребрами называется мультиграф.
Слайд 9Неориентированный граф
Граф G, рёбра которого не имеют определённого направления, называется
неориентированным.
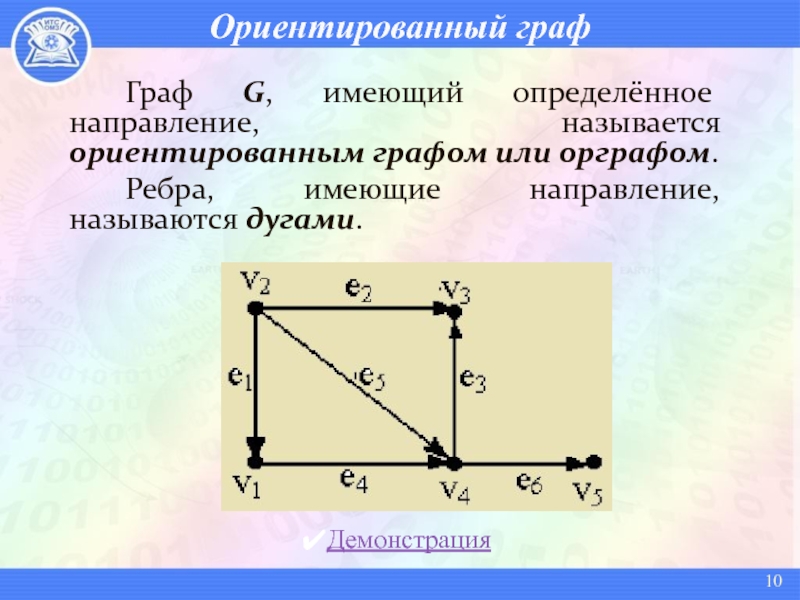
Слайд 10Ориентированный граф
Граф G, имеющий определённое направление, называется ориентированным графом или
орграфом.
Ребра, имеющие направление, называются дугами.
Демонстрация
Слайд 11Способы задания графов
1) Явное задание графа как алгебраической системы.
Чтобы задать
граф, достаточно для каждого ребра указать двухэлементное множество вершин –
его мы и будем отождествлять с ребром.{{a,b},{b,c},{a,c},{c,d}}
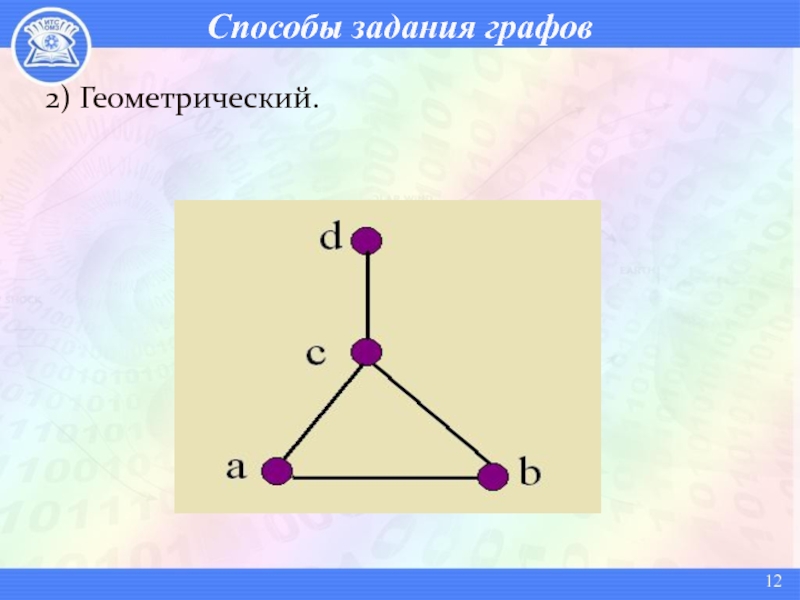
Слайд 13Способы задания графов
3) Матрица смежности.
Элементы Aij матрицы смежности A равны
количеству ребер между рассматриваемыми вершинами.
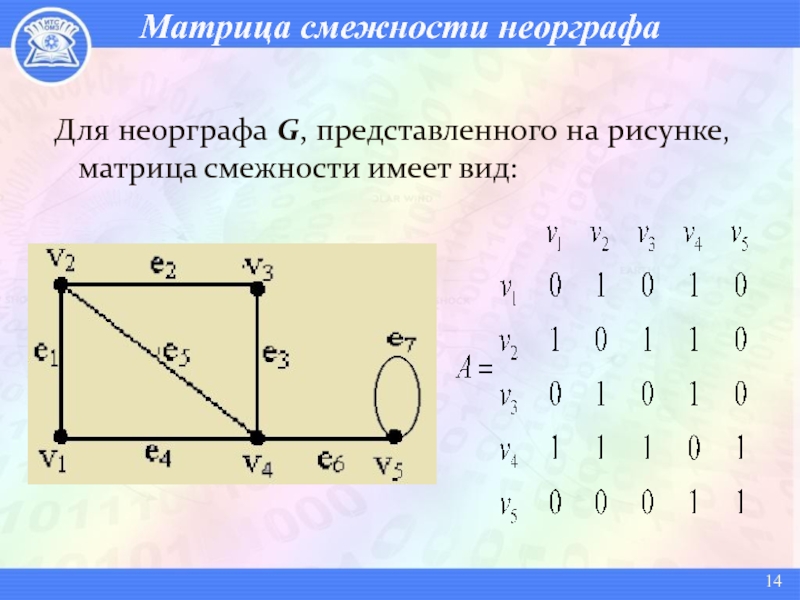
Слайд 14Матрица смежности неорграфа
Для неорграфа G, представленного на рисунке, матрица смежности
имеет вид:
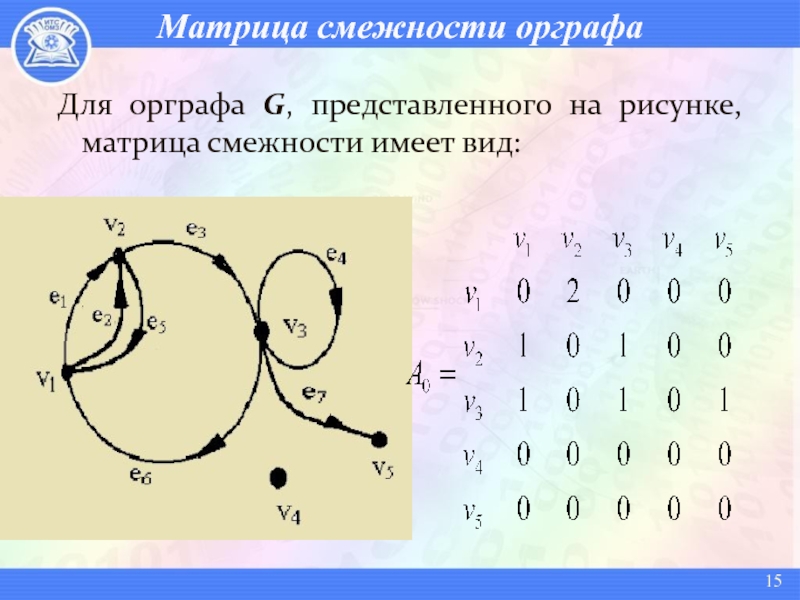
Слайд 15Матрица смежности орграфа
Для орграфа G, представленного на рисунке, матрица смежности
имеет вид:
Слайд 16Способы задания графов
4) Матрица инцидентности.
Матрица инцидентности В –это
таблица, строки которой соответствуют вершинам графа, а столбцы - ребрам.
Элементы матрицы определяются следующим образом:
Демонстрация
Слайд 17Способы задания графов
1) для неорграфа
1, если вершина vi инцидентна ребру
ej;
bij= 0, в противном случае
Слайд 18Матрица инцидентности орграфа
2) для орграфа
-1, если ребро ej входит в
вершину vi ;
1, если ребро ej выходит из вершины vi
;bij= 2, если ребро ej –петля из вершины vi ;
0, если ej и vi не инцидентны.
G
Слайд 19Маршрут
Маршрут в графе G=(V,E) — конечная чередующееся последовательность вершин и
ребер v0, e1, v1, e2,…,vk-1, ek, vk, которая начинается и
заканчивается на вершинах, причем vi-1 и vi являются концевыми вершинами ребра ei, 1≤ i ≤ k.
Слайд 20Маршрут
Маршрут называется открытым, если его концевые вершины различны (v1, e1,
v2, e2, v3, e3, v6, e9, v5, e7, v3, e11,
v6).Маршрут называется замкнутым, если его концевые вершины совпадают (v1, e1, v2, e2, v3, e7, v5, e3, v2, e4, v4, e5, v1).
G
Слайд 21Цепь
Маршрут называется цепью, если все его ребра различны.
Цепь называется простой,
если ее концевые вершины различны(v1, e1, v2, e2, v3, e8,
v6, e11, v3).Цепь называется замкнутой, если ее концевые вершины совпадают (v1,e1,v2,e2,v3,e7,v5,e3,v2,e4,v4,e5,v1).
G
Слайд 22Путь, цикл
Открытая цепь называется путем, если все ее вершины различны
(v1, e1, v2, e2, v3).
Цикл – это замкнутая цепь (
простой цикл, если цепь простая) (v1,e1,v2,e3,v5,e6,v4,e5,v1).Число ребер в пути называется длиной пути. Аналогично определяется длина цикла.
G
Слайд 23Cвойства путей и циклов
1. Степень каждой неконцевой вершины пути
равна 2, концевые вершины имеют степень, равную 1.
2. Каждая вершина
цикла имеет степень 2 или другую четную степень. Обращение этого утверждения, а именно то, что ребра подграфа, в котором каждая вершина имеет четную степень, образуют цикл, — неверно.3. Число вершин в пути на единицу больше числа ребер, тогда как в цикле число ребер равно числу вершин.
Слайд 24Связность графов, компонента связности
Две вершины vi и vj называются связанными
в графе G, если в нем существует путь vi—vj. Вершина
связана сама с собой.Граф называется связным, если в нем существует путь между каждой парой вершин.
Компонента связности – максимальный связный подграф в графе.
G
1 компонента связности: {v1, v2, v3, e1, e2, e3}
2 компонента связности: {v4, v5, v6, e4, e5, e6}
3 компонента связности: {v7, v8, e7}
4 компонента связности: {v9}
Демонстрация
Слайд 25Степень вершины
Степенью deg(vj) вершины vj называется число инцидентных ей ребер,
т. е. вершин в ее окружении.
Максимальная и минимальная степени вершин
графа G обозначаются символами Δ(G) и δ(G) соответственно:Δ(G)= δ(G)=
Граф G=(V,E) называется регулярным или однородным (степени r), если степени всех его вершин одинаковы. Степенью регулярного графа называется степень его вершин.
Слайд 26Сумма степеней вершин графа
Утверждение («лемма о рукопожатиях»)
Сумма всех вершин графа
– четное число, равное удвоенному числу ребер:
Интерпретация леммы: поскольку в
каждом рукопожатии участвуют две руки,то при любом числе рукопожатий общее число пожатых рук четно (при этом каждая рука учитывается столько раз, во скольких рукопожатиях она участвовала).Следствие
В любом графе число вершин нечетной степени четно
Слайд 27Изоморфизм графов
Два графа G1 и G2 изоморфны, если существует такое
взаимно-однозначное отображение между множествами их вершин и ребер, что соответствующие
ребра графов G1 и G2 инцидентны соответствующим вершинам этих графов.Если граф G изоморфен геометрическому графу G' в Rn, то G' называется геометрической реализацией графа G в пространстве Rn.
R3
R2
Граф R2 является геометрической реализацией графа R3
Слайд 28Пример изоморфных графов
Соответствие вершин: v1↔v2’,v2↔v3’,v3↔v1’,v4↔v4’,v5↔v5’;
Соответствие ребер:
e1↔e1’, e3↔e2’, e5↔e4’, e2↔e5’, e4↔e6’,
e6↔e3’.
G1 и G2 – изоморфные графы
G1 G2
Слайд 29Изоморфизм как отношение эквивалентности на множестве графов
Отношение изоморфизма является эквивалентностью,
т.е. оно симметрично, транзитивно и рефлексивно.
Слайд 30Помеченный и абстрактный графы
Граф порядка n называется помеченным, если его
вершинам присвоены некоторые метки (например номера 1, 2, …, n).
Абстрактный
(или непомеченный) граф – это класс изоморфных графов.Помеченные графы:
