Основы математической статистики

Содержание

1. Основы математической статистики
2. Законы теории вероятностей – это математическое выражение
3. Разработка методов получения, описания и анализа экспериментальных
4. Статистическими данными называются сведения о числе объектов
5. Выборочное исследование всегда предпочтительнее: а) по экономическим
6. Статистическая совокупность, состоящая из всех объектов, которые
7. Главная цель выборочного метода – по вычисленным
8. Изучаемое свойство объектов выборки должно соответствовать свойству
9. На практике всегда необходимо искать компромисс, чтобы
10. а) Статистический дискретный ряд распределенияПусть необходимо изучить
11. Пусть в полученной выборке наименьшее значение x1
12. Если результаты наблюдений представить в виде таблицы, то получим:Здесь p – относительная частота.
13. Такую таблицу называют статистическим дискретным рядом распределения.Cтатистический
14. Для графического изображения подобного ряда на координатной
15. Пример. Анализируемый показатель Х – срок лечения
16. Слайд 16
17. Очевидно, что представление результатов наблюдений в виде
18. Для построения такого ряда всю область наблюдаемых
19. Пусть, например все наблюдавшиеся значения признака Х
20. Слайд 20
21. Графическим изображением статистического интервального ряда распределения является
22. Слайд 22
23. Площадь каждого прямоугольника равна:илиПлощадь гистограммы частот равна n, а площадь гистограммы относительных частот равна 1.
24. Мода (Mo) равна варианте, которой соответствует наибольшая
25. Выборочная средняя – это среднее арифметическое вариант
26. Для характеристики рассеяния вариант вокруг среднего значения
27. Корень квадратный из выборочной дисперсии называют выборочным средним квадратическим отклонением.
28. Предположим, что генеральная совокупность является нормальным распределением.
29. Как и для выборки, для генеральной совокупности
30. Рассеяние значений изучаемого признака генеральной совокупности оценивают генеральной дисперсией или генеральным средним квадратическим отклонением.
31. а) Точечные оценкиОценка характеристики распределения называется точечной,
32. Наилучшей оценкой генеральной средней является средняя выборочная:
33. Наилучшей точечной оценкой генеральной дисперсии является так называемая исправленная выборочная дисперсия , определяемая по формуле:
34. Наилучшей точечной оценкой генерального среднего квадратического отклонения является исправленное выборочное среднее квадратическое отклонение.
35. Точечные оценки параметров генеральной совокупности справедливы лишь
36. Иначе говоря, р определяет вероятность того, что осуществляются следующие неравенства:где положительное число ε характеризует точность оценки.
37. Чем шире доверительный интервал, тем выше доверительная
38. Кроме доверительной вероятности, используют противоположное понятие – уровень значимости (вероятность непопадания генеральной средней в доверительный интервал).
39. При оценке генеральной средней по результатам выборочных
40. Определяют полуширину доверительного интервала для интервальной оценки генеральной средней при заданной доверительной вероятности р по формуле:
41. Интервальная оценка генеральной средней может быть использована
42. Если значения x1, x2, x3,…xi.рассматривать как варианты
43. Скачать презентанцию

Законы теории вероятностей – это математическое выражение реальных закономерностей, которым подчиняются массовые случайные явления. При этом каждое исследование случайных явлений, выполняемое методами теории вероятностей, прямо или косвенно опирается на экспериментальные данные,

Главная
Разное
Основы математической статистики

Слайды и текст этой презентации

Слайд 1ЛЕКЦИЯ № 2

по дисциплине «Физика, математика»
на тему: «Основы математической статистики»

для

курсантов и студентов I курса ФПВ, ФПиУГВ, спецфакультета

ВОЕННО–МЕДИЦИНСКАЯ АКАДЕМИЯ имени С.М.

Кирова Кафедра биологической и медицинской физики

ЛЕКЦИЯ № 2по дисциплине «Физика, математика»на тему: «Основы математической статистики» для курсантов и студентов I курса ФПВ, ФПиУГВ,

Слайд 2
Законы теории вероятностей – это математическое выражение реальных закономерностей, которым

подчиняются массовые случайные явления. При этом каждое исследование случайных явлений,

выполняемое методами теории вероятностей, прямо или косвенно опирается на экспериментальные данные, на результаты испытаний и наблюдений.

Законы теории вероятностей – это математическое выражение реальных закономерностей, которым подчиняются массовые случайные явления. При этом каждое

Слайд 3
Разработка методов получения, описания и анализа экспериментальных данных, определенных в

результате исследования массовых случайных явлений, составляет предмет специальной науки –

математической статистики.

Разработка методов получения, описания и анализа экспериментальных данных, определенных в результате исследования массовых случайных явлений, составляет предмет

Слайд 4Статистическими данными называются сведения о числе объектов в какой-либо более

или менее обширной совокупности, обладающих теми или иными признаками.
Предположим,

что необходимо изучить множество объектов по какому-либо признаку. Это возможно сделать, либо произведя сплошное наблюдение (исследование, измерение), либо не сплошное (выборочное).

1. Основные понятия математической статистики

Статистическими данными называются сведения о числе объектов в какой-либо более или менее обширной совокупности, обладающих теми или

Слайд 5Выборочное исследование всегда предпочтительнее:
а) по экономическим причинам (меньшая трудоемкость),

б) часто сплошное обследование нереально (необходимо уничтожить все исследуемые объекты,

невозможно обследовать все население Земли и т.п.).

Выборочное исследование всегда предпочтительнее: а) по экономическим причинам (меньшая трудоемкость), б) часто сплошное обследование нереально (необходимо уничтожить

Слайд 6Статистическая совокупность, состоящая из всех объектов, которые (по крайней мере

теоретически) подлежат исследованию, называется генеральной совокупностью, а множество объектов, отобранных

из нее по определенным правилам – выборочной совокупностью (выборкой).

Статистическая совокупность, состоящая из всех объектов, которые (по крайней мере теоретически) подлежат исследованию, называется генеральной совокупностью, а

Слайд 7Главная цель выборочного метода – по вычисленным числовым характеристикам выборки

как можно точнее определить соответствующие характеристики генеральной совокупности.

Главная цель выборочного метода – по вычисленным числовым характеристикам выборки как можно точнее определить соответствующие характеристики генеральной

Слайд 8Изучаемое свойство объектов выборки должно соответствовать свойству объектов генеральной совокупности,

то есть выборка должна быть представительной (репрезентативной).
Случайность отбора –

обязательное условие репрезентативности выборки.
Свойства выборочной совокупности тем лучше отражают свойства генеральной совокупности, чем больше объектов содержит эта выборочная совокупность (т.е. чем больше ее объем).

Изучаемое свойство объектов выборки должно соответствовать свойству объектов генеральной совокупности, то есть выборка должна быть представительной (репрезентативной).

Слайд 9
На практике всегда необходимо искать компромисс, чтобы исследуемые выборки были,

с одной стороны, не слишком велики, а с другой –

репрезентативны.

На практике всегда необходимо искать компромисс, чтобы исследуемые выборки были, с одной стороны, не слишком велики, а

Слайд 10а) Статистический дискретный ряд распределения
Пусть необходимо изучить распределение значений признака

Х у объектов некоторой генеральной совокупности.
С этой целью из данной

генеральной совокупности извлекают некоторую выборочную совокупность объемом n.

2. Статистическое распределение выборки

а) Статистический дискретный ряд распределенияПусть необходимо изучить распределение значений признака Х у объектов некоторой генеральной совокупности.С этой

Слайд 11Пусть в полученной выборке наименьшее значение x1 признака встречается m1

раз, следующее по величине значение x1 – m2 раз, и

так далее, до хk – mk раз.
Наблюдаемые значения признака (x1, x2, x3 и т.д.) принято называть вариантами, а числа m1, m2, m3, …mk – их частотами.
Естественно, что сумма всех частот равна объему выборки (n ).

m1 + m2 + m3 +…+ mk = n

Пусть в полученной выборке наименьшее значение x1 признака встречается m1 раз, следующее по величине значение x1 –

Слайд 12Если результаты наблюдений представить в виде таблицы, то получим:

Здесь p

– относительная частота.

Слайд 13Такую таблицу называют статистическим дискретным рядом распределения.
Cтатистический дискретный ряд распределения

– это совокупность вариант и соответствующих им частот (или относительных

частот).
В медицинской литературе статистическое распределение, состоящее из вариант и соответствующих им частот, получило название вариационного ряда.

Такую таблицу называют статистическим дискретным рядом распределения.Cтатистический дискретный ряд распределения – это совокупность вариант и соответствующих им

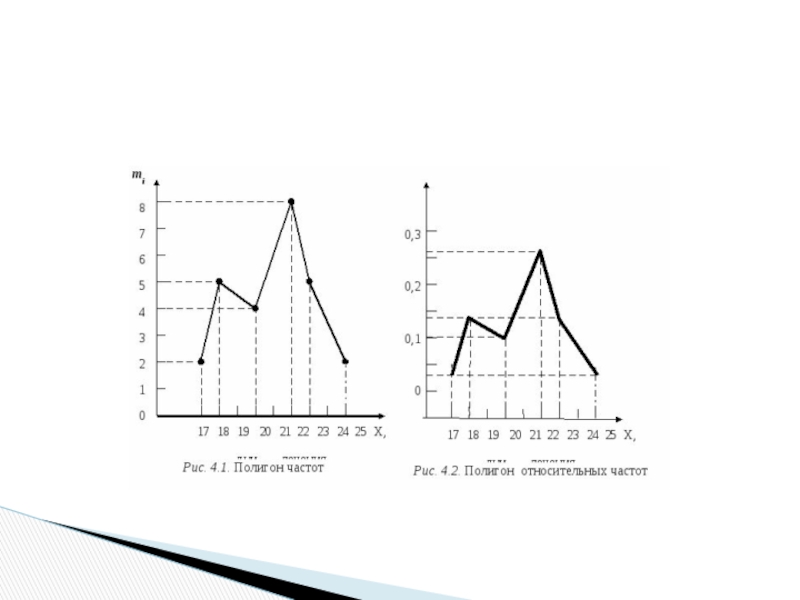
Слайд 14Для графического изображения подобного ряда на координатной плоскости откладывают точки

(xi; mi) и соединяют их отрезками прямых. Такую ломаную линию,

являющуюся графическим представлением дискретного статистического ряда распределения, называют полигоном частот.

Для графического изображения подобного ряда на координатной плоскости откладывают точки (xi; mi) и соединяют их отрезками прямых.

Слайд 15Пример. Анализируемый показатель Х – срок лечения больного при некотором

заболевании. Вариационный ряд – распределение больных по срокам лечения (объем

выборки n = 26 больных) – имеет вид:

Пример. Анализируемый показатель Х – срок лечения больного при некотором заболевании. Вариационный ряд – распределение больных по

Слайд 16

Слайд 17Очевидно, что представление результатов наблюдений в виде статистического дискретного ряда

распределения на практике удобно лишь в случае ограниченного (не более

10-20) количества различающихся между собой вариант в выборочной совокупности.
Если же количество таких вариант существенно больше, то результаты представляют в виде статистического интервального ряда распределения.

б) Статистический интервальный ряд распределения

Очевидно, что представление результатов наблюдений в виде статистического дискретного ряда распределения на практике удобно лишь в случае

Слайд 18Для построения такого ряда всю область наблюдаемых значений изучаемого признака

Х разбивают на некоторое небольшое количество равных по величине интервалов

и фиксируют количество значений признака, принадлежащих каждому интервалу (суммe частот вариант, попавших в этот интервал).

Для построения такого ряда всю область наблюдаемых значений изучаемого признака Х разбивают на некоторое небольшое количество равных

Слайд 19Пусть, например все наблюдавшиеся значения признака Х принадлежат интервалу (a,b).

Разделим этот интервал на k равных частей (частичных интервалов) длиной

Δх = (b-a)|k и обозначим точки деления как x0=a, x1, x2, …, xk-1, xk=b.
Если частоты интервалов равны, соответственно, m1, m2, …, mk, то можно составить таблицу, в первой строке которой перечислить все частичные интервалы, а во второй соответствующие им частоты (или относительные частоты):

Пусть, например все наблюдавшиеся значения признака Х принадлежат интервалу (a,b). Разделим этот интервал на k равных частей

Слайд 20

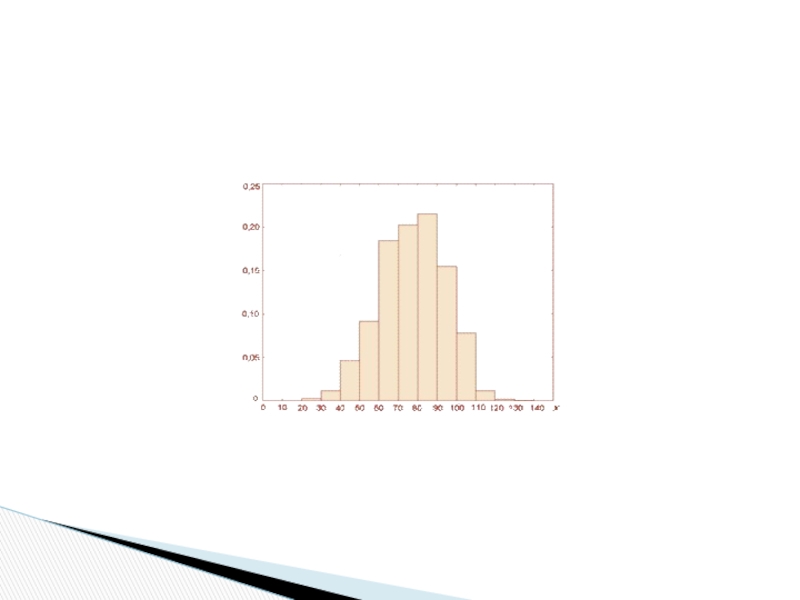
Слайд 21Графическим изображением статистического интервального ряда распределения является фигура, называемая полигоном

частот (или относительных частот). Это совокупность смежных прямоугольников, основания которых

равны Δх, а высоты – отношению mi / Δх (или pi / Δх).

Графическим изображением статистического интервального ряда распределения является фигура, называемая полигоном частот (или относительных частот). Это совокупность смежных

Слайд 22

Слайд 23Площадь каждого прямоугольника равна:

или
Площадь гистограммы частот равна n, а площадь

гистограммы относительных частот равна 1.

Слайд 24
Мода (Mo) равна варианте, которой соответствует наибольшая частота.
Медиана (Ме) равна

варианте, которая расположена в середине статистического распределения. Она делит вариационный

ряд на две равные части. При четном числе вариант за медиану принимают среднее значение из двух центральных вариант.

3. Выборочные характеристики распределения

Мода (Mo) равна варианте, которой соответствует наибольшая частота.Медиана (Ме) равна варианте, которая расположена в середине статистического распределения.

Слайд 25Выборочная средняя – это среднее арифметическое вариант статистического ряда.

где mi

– частота встречаемости значения xi в выборке,
k – количество

различающихся между собой значений признака (количество вариант),
n – объем выборки.

Выборочная средняя – это среднее арифметическое вариант статистического ряда.где mi – частота встречаемости значения xi в выборке,

Слайд 26Для характеристики рассеяния вариант вокруг среднего значения вводят характеристику, называемую

выборочной дисперсией – среднее арифметическое квадратов отклонения вариант от их

среднего значения.

Слайд 27Корень квадратный из выборочной дисперсии называют выборочным средним квадратическим отклонением.

Слайд 28Предположим, что генеральная совокупность является нормальным распределением. Нормальное распределение полностью

определено математическим ожиданием и средним квадратическим отклонением. Поэтому, если по

выборке можно оценить, то есть приближенно найти, эти параметры, то будет решена одна из задач математической статистики – определение параметров большого массива по исследованию его части.

4. Оценка параметров генеральной совокупности по ее выборке. Точечные оценки.

Предположим, что генеральная совокупность является нормальным распределением. Нормальное распределение полностью определено математическим ожиданием и средним квадратическим отклонением.

Слайд 29Как и для выборки, для генеральной совокупности можно определить генеральную

среднюю - среднее арифметическое значение всех величин, составляющих генеральную совокупность

(учитывая большой объем этой совокупности, можно считать, что генеральная средняя равна математическому ожиданию).

Как и для выборки, для генеральной совокупности можно определить генеральную среднюю - среднее арифметическое значение всех величин,

Слайд 30
Рассеяние значений изучаемого признака генеральной совокупности оценивают генеральной дисперсией или

генеральным средним квадратическим отклонением.

Рассеяние значений изучаемого признака генеральной совокупности оценивают генеральной дисперсией или генеральным средним квадратическим отклонением.

Слайд 31
а) Точечные оценки
Оценка характеристики распределения называется точечной, если она определяется

одним числом, которому приближенно равна оцениваемая характеристика.

а) Точечные оценкиОценка характеристики распределения называется точечной, если она определяется одним числом, которому приближенно равна оцениваемая характеристика.

Слайд 32Наилучшей оценкой генеральной средней является средняя выборочная:

Слайд 33Наилучшей точечной оценкой генеральной дисперсии является так называемая исправленная выборочная

дисперсия , определяемая по формуле:

Слайд 34Наилучшей точечной оценкой генерального среднего квадратического отклонения является исправленное выборочное

среднее квадратическое отклонение.

Наилучшей точечной оценкой генерального среднего квадратического отклонения является исправленное выборочное среднее квадратическое отклонение.

Слайд 35Точечные оценки параметров генеральной совокупности справедливы лишь при достаточно большом

объеме выборки. При небольшом объеме выборки пользуются интервальными оценками.
В этом

случае указывается интервал (доверительный интервал), в котором с определенной (как правило, заранее заданной) вероятностью р (доверительной вероятностью) находится генеральная средняя.

б) Интервальная оценка генеральной средней

Точечные оценки параметров генеральной совокупности справедливы лишь при достаточно большом объеме выборки. При небольшом объеме выборки пользуются

Слайд 36Иначе говоря, р определяет вероятность того, что осуществляются следующие неравенства:

где

положительное число ε характеризует точность оценки.

Иначе говоря, р определяет вероятность того, что осуществляются следующие неравенства:где положительное число ε характеризует точность оценки.

Слайд 37
Чем шире доверительный интервал, тем выше доверительная вероятность, и наоборот.

При решении статистических задач в фармации, медицине и биологии доверительную

вероятность, как правило, принимают равной 0,95 (реже – 0,99).

Чем шире доверительный интервал, тем выше доверительная вероятность, и наоборот. При решении статистических задач в фармации, медицине

Слайд 38Кроме доверительной вероятности, используют противоположное понятие – уровень значимости (вероятность

непопадания генеральной средней в доверительный интервал).

Кроме доверительной вероятности, используют противоположное понятие – уровень значимости (вероятность непопадания генеральной средней в доверительный интервал).

Слайд 39При оценке генеральной средней по результатам выборочных наблюдений в предположении

нормального распределения признака в генеральной совокупности доверительный интервал для заданной

доверительной вероятности находят следующим методом:

При оценке генеральной средней по результатам выборочных наблюдений в предположении нормального распределения признака в генеральной совокупности доверительный

Слайд 40Определяют полуширину доверительного интервала для интервальной оценки генеральной средней при

заданной доверительной вероятности р по формуле:

Определяют полуширину доверительного интервала для интервальной оценки генеральной средней при заданной доверительной вероятности р по формуле:

Слайд 41Интервальная оценка генеральной средней может быть использована для оценки истинного

значения измеряемой величины.
Пусть несколько раз измеряют одну и ту

же физическую величину. При этом по разным случайным причинам получают разные значения: x1, x2, x3,…xi. Будем считать, что нет преобладающего влияния какого-либо фактора на эти измерения.

в) Интервальная оценка истинного значения измеряемой величины

Интервальная оценка генеральной средней может быть использована для оценки истинного значения измеряемой величины. Пусть несколько раз измеряют

Слайд 42Если значения x1, x2, x3,…xi.рассматривать как варианты выборки, а истинное

значение измеряемой величины как аналог генеральной средней, то можно по

описанным выше правилам определить доверительный интервал, в который с доверительной вероятностью р попадает истинное значение измеряемой величины.

Если значения x1, x2, x3,…xi.рассматривать как варианты выборки, а истинное значение измеряемой величины как аналог генеральной средней,

Скачать презентацию

Разделы презентаций