Параллельность прямых, прямой и плоскости

лежат в одной плоскости и не пересекаются.
  
Параллельность прямых a и b обозначается так: a∥b или b∥a.
 
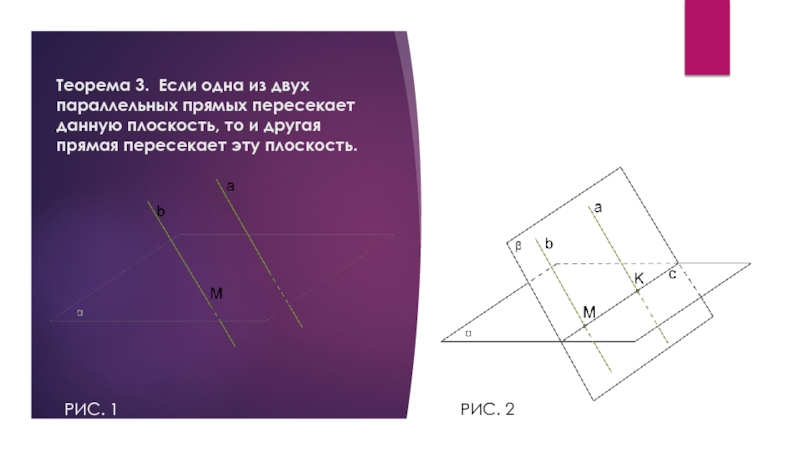
Teорема

1.  Через две параллельные прямые можно провести плоскость, и при том только одну.

Доказательство:
1. Так как прямые a и b параллельны, из определения следует, что через них можно провести плоскость α.
2. Чтобы доказать, что такая плоскость только одна, на прямой a обозначаем точки B и C, а на прямой b точку A.
3. Так как через три точки, которые не лежат на одной прямой, можно провести только одну плоскость (2 аксиома), то α является единственной плоскостью, которой принадлежат прямые a и b.

провести прямую, параллельную данной прямой, и при том только одну.
Доказательство:
1. Через

данную прямую a и точку M, которая не лежит на прямой, проводится плоскость α.
2. Такая плоскость только одна (т.к. через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну).
3. А в плоскости α через точку M можно провести только одну прямую b, которая параллельна прямой a.

плоскость, то и другая прямая пересекает эту плоскость.

Рис. 1

Рис. 2

1-ой теоремы известно, что через параллельные прямые a и b можно провести только одну

плоскость β.
 
Так как точка M находится на прямой b, то M также принадлежит плоскости β(2. рис.). Если у плоскостей α и β есть общая точка M, то у этих плоскостей есть общая прямая c, которая является прямой пересечения этих плоскостей (4 аксиома).
 
Прямые a, b и c находятся в плоскости β.
Если в этой плоскости одна из параллельных прямых b пересекает прямую c, то вторая прямая a тоже пересекает c.
 
Точку пересечения прямых a и c обозначим за K.
Так как точка K находится на прямой c, то K находится в плоскости α и является единственной общей точкой прямой a и плоскости α.
Значит, прямая a пересекает плоскость α в точке K.

эту точку, можно провести только одну плоскость α (Через прямую и не

лежащую на ней точку можно провести только одну плоскость).
 
Возможны два случая:
1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.
 
Пусть прямая b пересекает плоскость α.
Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может
одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно,  предположение, что прямая b пересекает плоскость α, является неверным.
Значит, прямая b находится в плоскости α.
 
Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L.
Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.
Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.
 
Всё множество прямых в пространстве, которые параллельны данной прямой, называется пучком параллельных прямых.

Выводы:
1) Любые две прямые пучка параллельных прямых параллельны между собой.
2) Параллельности прямых в пространстве присуща транзитивность: если a∥b и b∥c ,то a∥c.

находятся в некоторой плоскости, то прямая лежит в этой плоскости.

Отсюда следует, что возможны три случая взаимного расположения прямой и плоскости в пространстве:
1) прямая лежит (находится) в плоскости
2) прямая и плоскость имеют только одну общую точку (прямая и плоскость пересекаются)
3) прямая и плоскость не имеют общих точек
 
Прямая и плоскость называются параллельными, если они не имеют общих точек.

в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то

эта прямая параллельна данной плоскости. 

в некоторой точке A.
Причем A не находится на b, так как a∥b. Согласно признаку

скрещивающихся прямых, прямые a и b скрещивающиеся. 

Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися.
Значит прямая a должна быть параллельна плоскости α.

эту плоскость по прямой b, то b∥a.
Прямую b иногда называют следом плоскости β на плоскости α.
  
Теорема 7. Если

одна из двух параллельных прямых a∥b параллельна данной плоскости α, то другая прямая либо параллельна этой плоскости
либо лежит в этой плоскости.