Перемещения при изгибе

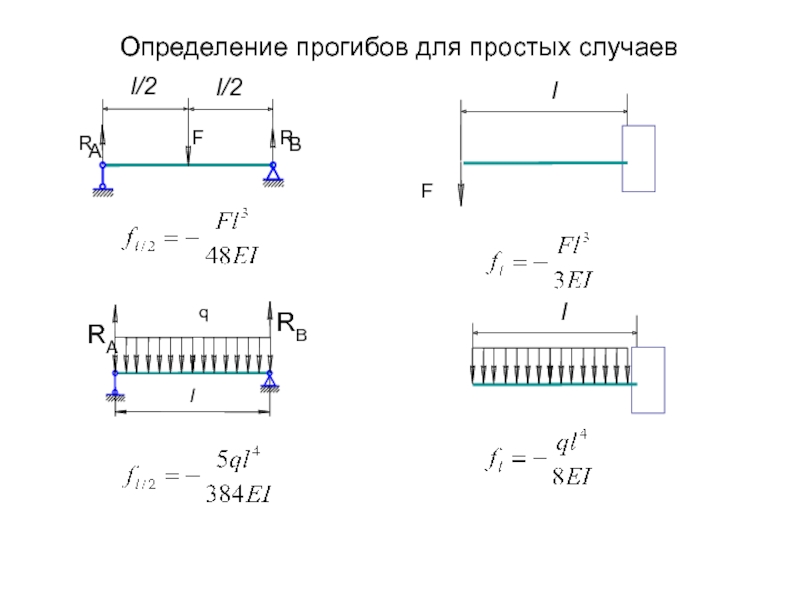
балки под действием приложенных нагрузок и подбор таких размеров поперечного

сечения, при которых перемещения не будут превышать установленных нормами пределов.

Перемещение центра тяжести сечения по направлению перпендикулярному к оси балки, называется прогибом. Прогиб обозначается буквой w

Наибольший прогиб в пролете или на консоли балки, называется стрелой прогиба и обозначается буквой f.

Угол, , на который каждое сечение поворачивается по отношению к своему первоначальному положению и есть угол поворота.

Угол поворота считается положительным, при повороте сечения против хода часовой стрелки

Угол поворота сечения равен значению производной от прогиба по координате Z в этом же сечении, то есть:

Условие жесткости при изгибе

линии балки. Это метод непосредственного интегрирования, метод Клебша и метод

начальных параметров.

Проинтегрировав уравнение упругой линии балки первый раз, получают выражение для определения углов поворота:

Интегрируя второй раз, находят выражения для определения прогибов:

Метод непосредственного интегрирования

Значения постоянных интегрирования С и D определяют из начальных условий на опорах балки

основные условия:
начало координат, для всех участков, необходимо расположить в крайнем

левом конце балки;
интегрирование дифференциального уравнения упругой линии балки проводить, не раскрывая скобок;
при включении в уравнение внешнего сосредоточенного момента М его необходимо помножить на (Z-a)0 где а - координата сечения, в котором приложен момент;
в случае обрыва распределенной нагрузки ее продлевают до конца балки, а для восстановления действительных условий нагружения вводят «компенсирующую» нагрузку обратного направления

поворота сечения, w—прогиб, 0 - угол поворота в начале координат,

w0—прогиб в начале координат, di—расстояние от начало координат до i-той опоры балки, ai—расстояние от начало координат до точки приложения сосредоточенного момента Mi , bi—расстояние от начало координат до точки приложения сосредоточенной силы Fi , сi—расстояние от начало координат до начала участка распределенной нагрузки qi , Ri и Мрi—реакция и реактивный момент в опорах балки.