Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Плоские и планарные графы
Содержание
- 1. Плоские и планарные графы
- 2. 1. Эйлеровым путем (циклом) называется . .
- 3. Рассмотренные ранее задачи – это задачи на
- 4. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯГраф, изображенный на плоскости, называется плоским,
- 5. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯДва графа G1 и G2 называются
- 6. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯГраф называется планарным, если он изоморфен
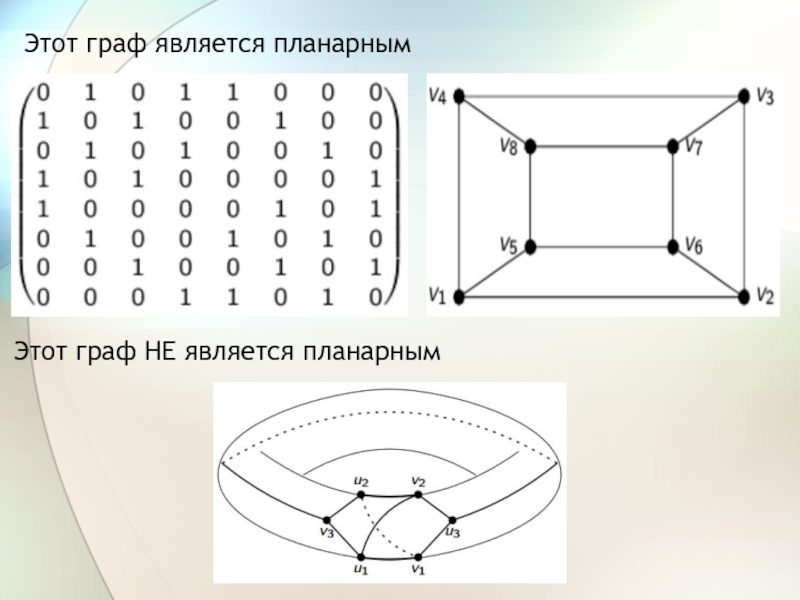
- 7. Этот граф является планарнымЭтот граф НЕ является планарным
- 8. ТЕОРЕМА ЭЙЛЕРА О ПЛОСКИХ ГРАФАХЕсли плоскость разрезать
- 9. ТЕОРЕМА ЭЙЛЕРА О ПЛОСКИХ ГРАФАХДва изоморфных плоских графа имеют одинаковое число граней
- 10. УСЛОВИЯ ПЛАНАРНОСТИГрафы G1 и G2 называются гомеоморфными,
- 11. ЗАДАЧА О ПОЛНОМ ГРАФЕ, ИМЕЮЩЕМ ПЯТЬ ВЕРШИНЛюбой полный граф, имеющий пять вершин, неплоскийГрафы Куратовского
- 12. Теорема Понтрягина — КуратовскогоГраф планарен тогда и
- 13. удалили ребра (z1;z4) и (z2;z3)граф G1 изоморфен
- 14. Теорема ВагнераОбыкновенный граф G планарен тогда и
- 15. КОНЕЦ 1 СЕРИИ СЕЗОНА 8В следующей серии
- 16. РАСКРАСКА ГРАФОВ
- 17. ПОСТАНОВКА ЗАДАЧИ РАСКРАСКИДана политическая карта мира. Требуется
- 18. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯПри раскраске элементам графа ставятся в
- 19. Задача раскраски карты может быть переформулирована следующим
- 20. ВИДЫ РАСКРАСКИРаскраска вершинРаскраска вершин — главная задача
- 21. АЛГОРИТМЫ РАСКРАСКИЖадная раскраскаЖадный алгоритм упорядочивает вершины v_{1},…,v_{n}
- 22. ПРИМЕНЕНИЕРаспределение регистров Компилятор — это компьютерная
- 23. ЗАДАЧА СОСТАВЛЕНИЯ РАСПИСАНИЯВ студенческих группах 26-К и
- 24. РЕШЕНИЕПостроим граф с вершинами А1, А2, Д1,
- 25. ЗАДАЧА РАСПРЕДЕЛЕНИЯ ОБОРУДОВАНИЯИмеется некоторое количество работ и
- 26. Слайд 26
- 27. АЛГОРИТМ РАСКРАСКИ1. Упорядочить вершины по невозрастанию степени.
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Плоские и планарные графы
1. Основные определения
2. Свойства планарных графов
3. Теорема
Понтрягина-Куратовского
Слайд 21. Эйлеровым путем (циклом) называется . . .
2. Связный граф
эйлеров тогда и только тогда . . .
3. Если граф
G(V,E) обладает эйлеровым циклом, то он . . .4. Эйлеров путь в связном графе существует тогда и только тогда, когда в нем имеется не более . . .
двух ребер, связанных с одной вершиной
двух вершин четной степени
двух вершин нечетной степени
трех ребер, сходящихся к одной вершине
5. Алгоритм поиска эйлерова цикла . . .
ПОВТОРЕНИЕ И ПРЕДЫДУЩИХ ЗАНЯТИЙ
Слайд 3Рассмотренные ранее задачи – это задачи на алгебраическое понятие графа.
Однако
в теории графов встречаются и задачи, в которых граф рассматривается
как геометрическая фигура (или геометрическое «изображение» графа, заданного алгебраически)При прокладке различных коммуникаций может требоваться, чтобы их линии не пересекались (пример – головоломка о домах и колодцах). Аналогичная проблема существует в электротехнике при проектировании и изготовлении печатных плат.
Слайд 4ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Граф, изображенный на плоскости, называется плоским, если его ребра
не пересекаются в точках, отличных от вершин графа.
Каждый граф укладывается
в трехмерное пространствоОдин и тот же граф (как множество вершин + множество ребер) может иметь как плоские, так и не плоские изображения
Принципиальный вопрос, на который нужно отвечать при решении задач типа прокладки коммуникаций, это:
имеет ли данный граф хотя бы одно плоское изображение?
Слайд 5ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
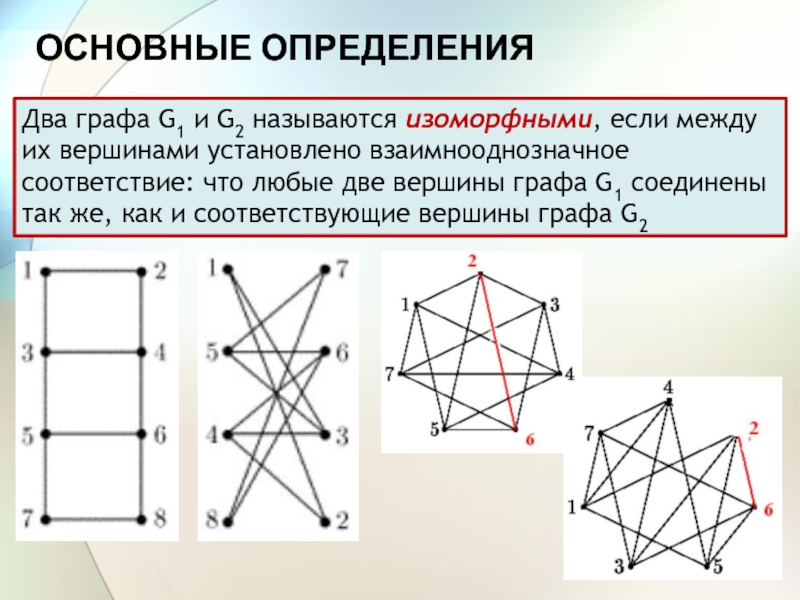
Два графа G1 и G2 называются изоморфными, если между
их вершинами установлено взаимнооднозначное соответствие: что любые две вершины графа
G1 соединены так же, как и соответствующие вершины графа G2Слайд 6ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
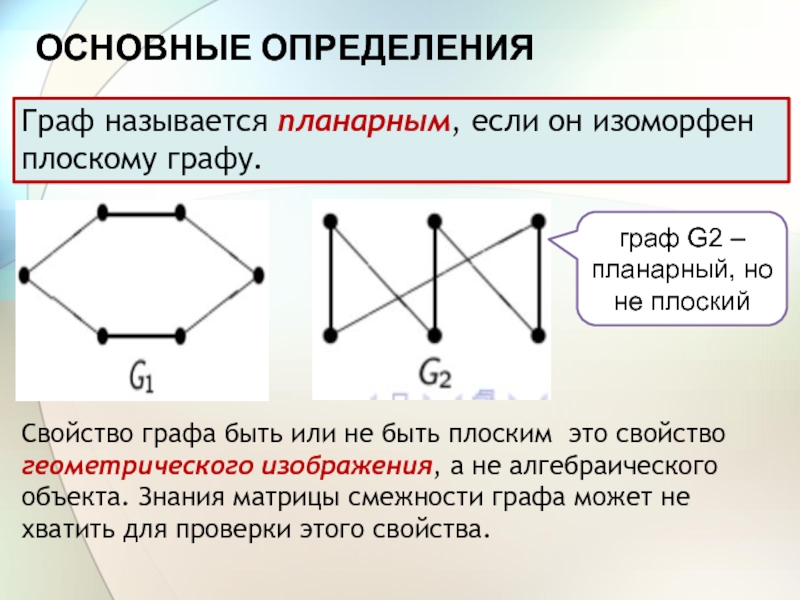
Граф называется планарным, если он изоморфен плоскому графу.
граф G2
– планарный, но не плоский
Свойство графа быть или не быть
плоским это свойство геометрического изображения, а не алгебраического объекта. Знания матрицы смежности графа может не хватить для проверки этого свойства.Слайд 8ТЕОРЕМА ЭЙЛЕРА О ПЛОСКИХ ГРАФАХ
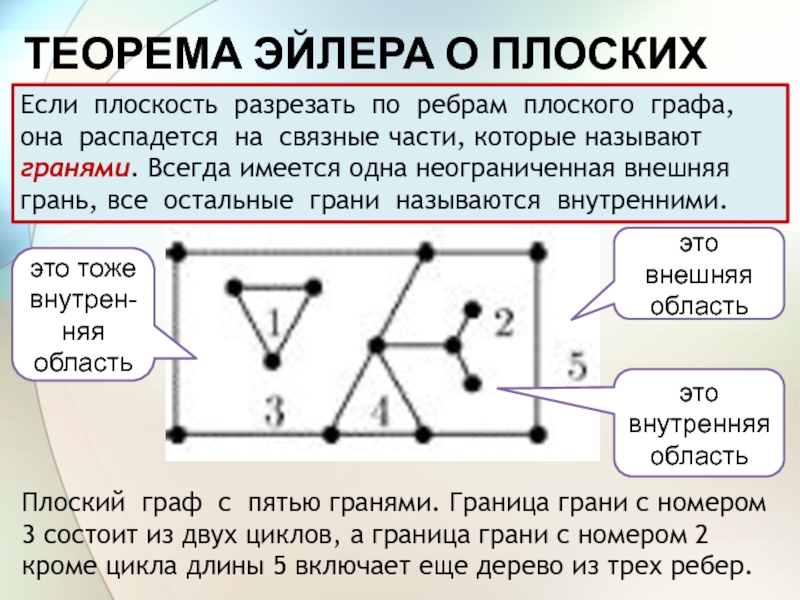
Если плоскость разрезать по ребрам плоского
графа, она распадется на связные части, которые называют гранями. Всегда
имеется одна неограниченная внешняя грань, все остальные грани называются внутренними.Плоский граф с пятью гранями. Граница грани с номером 3 состоит из двух циклов, а граница грани с номером 2 кроме цикла длины 5 включает еще дерево из трех ребер.
это внешняя область
это внутренняя область
это тоже внутрен-няя область
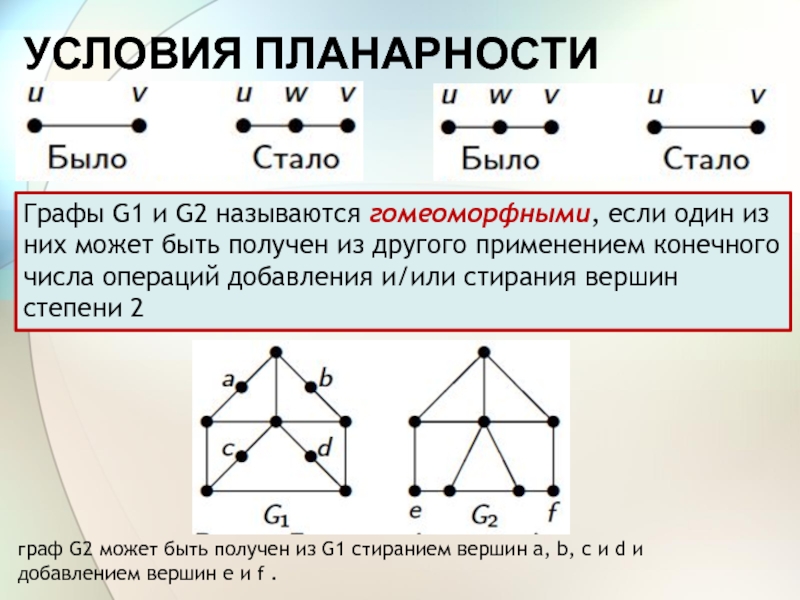
Слайд 10УСЛОВИЯ ПЛАНАРНОСТИ
Графы G1 и G2 называются гомеоморфными, если один из
них может быть получен из другого применением конечного числа операций
добавления и/или стирания вершин степени 2граф G2 может быть получен из G1 стиранием вершин a, b, c и d и
добавлением вершин e и f .
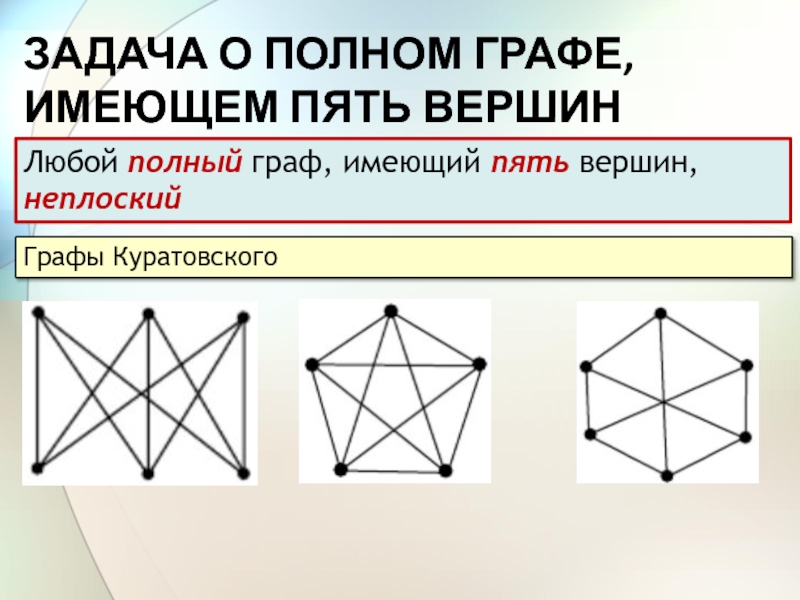
Слайд 11ЗАДАЧА О ПОЛНОМ ГРАФЕ, ИМЕЮЩЕМ ПЯТЬ ВЕРШИН
Любой полный граф, имеющий
пять вершин, неплоский
Графы Куратовского
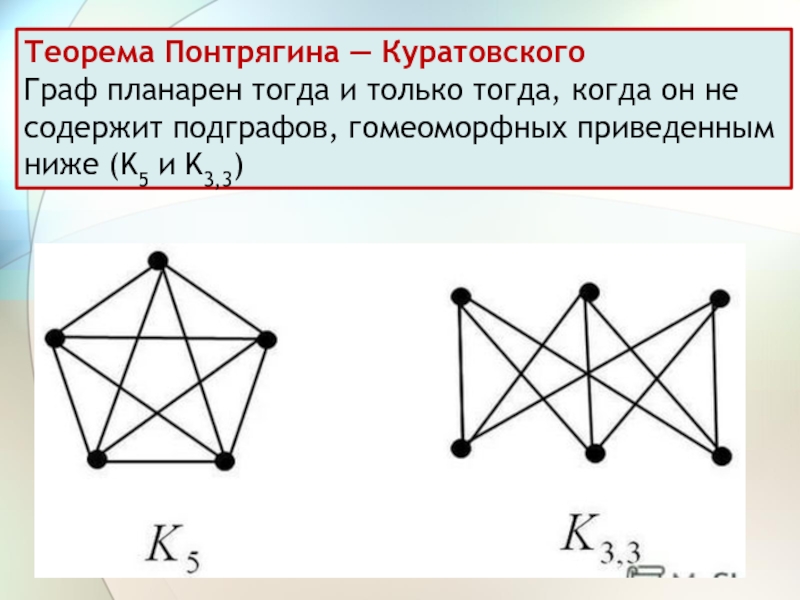
Слайд 12Теорема Понтрягина — Куратовского
Граф планарен тогда и только тогда, когда
он не содержит подграфов, гомеоморфных приведенным ниже (K5 и K3,3)
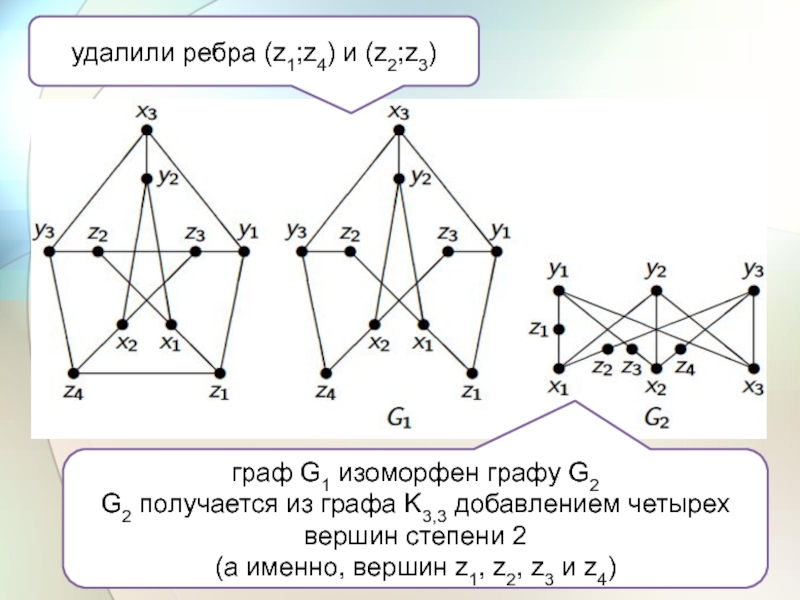
Слайд 13удалили ребра (z1;z4) и (z2;z3)
граф G1 изоморфен графу G2
G2
получается из графа K3,3 добавлением четырех вершин степени 2
(а именно,
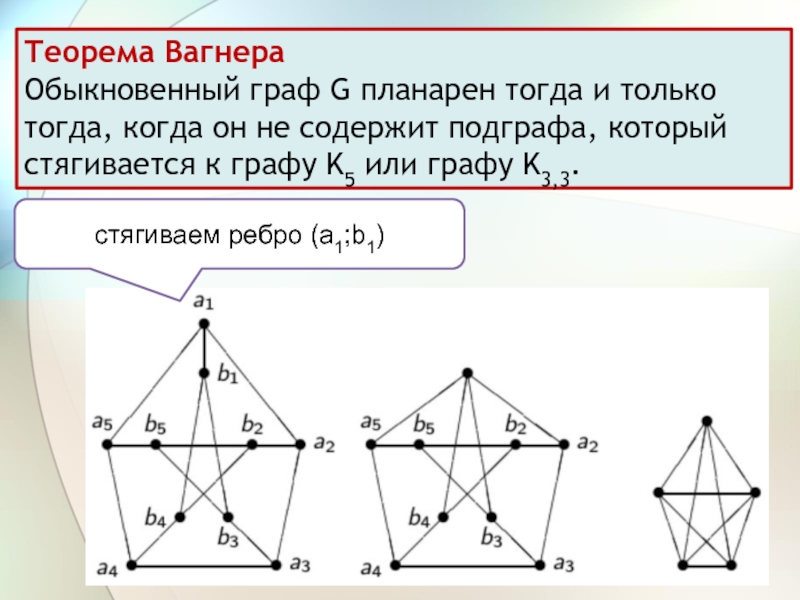
вершин z1, z2, z3 и z4)Слайд 14Теорема Вагнера
Обыкновенный граф G планарен тогда и только тогда, когда
он не содержит подграфа, который стягивается к графу K5 или
графу K3,3.стягиваем ребро (a1;b1)
Слайд 15КОНЕЦ 1 СЕРИИ СЕЗОНА 8
В следующей серии вы увидите:
как красят
политическую карту мира;
тайна создания расписаний занятий в группах 26, 28,
18к11;к чему приводит жадность при раскраске графов
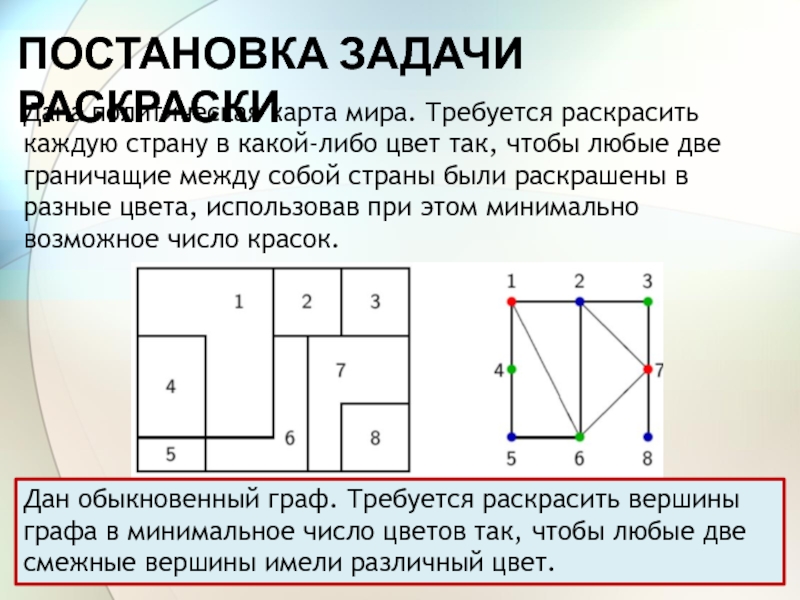
Слайд 17ПОСТАНОВКА ЗАДАЧИ РАСКРАСКИ
Дана политическая карта мира. Требуется раскрасить каждую страну
в какой-либо цвет так, чтобы любые две граничащие между собой
страны были раскрашены в разные цвета, использовав при этом минимально возможное число красок.Дан обыкновенный граф. Требуется раскрасить вершины графа в минимальное число цветов так, чтобы любые две смежные вершины имели различный цвет.
Слайд 18ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
При раскраске элементам графа ставятся в соответствие метки (числа)
из множества k (k = 1, 2, 3, ... );
эти метки традиционно называются «цветами».способ окраски вершин графа, при котором любым двум смежным вершинам соответствуют разные цвета, называется раскраской вершин.
Раскраска графа называется правильной, если любые две смежные вершины графа имеют разные цвета из множества цветов k (k = 1, 2, 3, ... )
Раскраска с использованием k цветов называется k-раскраской. Наименьшее число цветов, необходимое для раскраски графа G, называется его хроматическим числом.
Слайд 19Задача раскраски карты может быть переформулирована следующим образом: Найти хроматическое
число данного планарного графа.
Когда говорят о раскраске графов, почти всегда
подразумевают под этим раскраску их вершинЭтот граф может быть раскрашен 3 цветами 12 способами
Слайд 20ВИДЫ РАСКРАСКИ
Раскраска вершин
Раскраска вершин — главная задача раскраски графов,
все
остальные задачи в этой области могут быть сведены к ней.
Рёберная раскраска
графа подразумевает назначение цветов ребрам так, что никакие два ребра одного цвета не принадлежат одной вершине. Наименьшее число цветов, необходимое для рѐберной раскраски графа G — это его хроматический
индекс, или рёберное хроматическое число
Тотальная раскраска
—такое присвоение цветов, что ни соседние вершины, ни смежные ребра, ни вершины и ребра, которые их соединяют, не имеют одинакового цвета
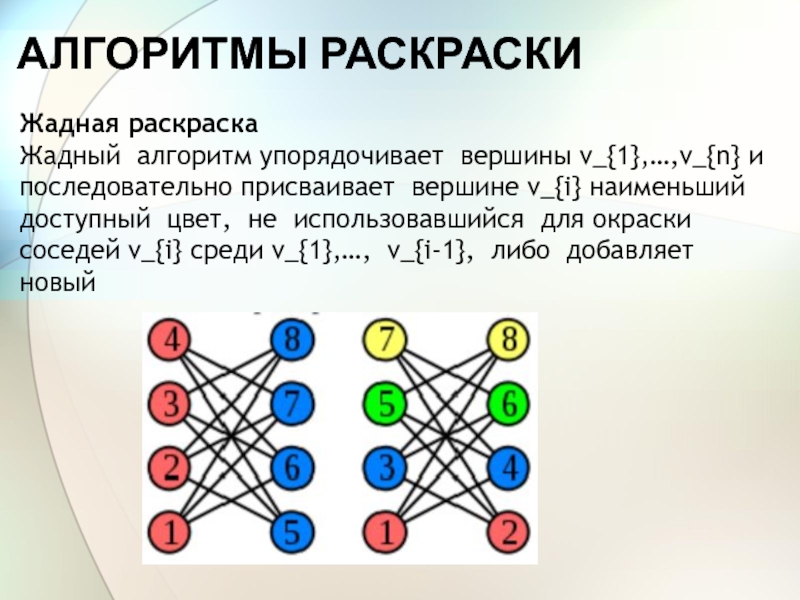
Слайд 21АЛГОРИТМЫ РАСКРАСКИ
Жадная раскраска
Жадный алгоритм упорядочивает вершины v_{1},…,v_{n} и последовательно присваивает
вершине v_{i} наименьший доступный цвет, не использовавшийся для окраски соседей
v_{i} среди v_{1},…, v_{i-1}, либо добавляет новыйСлайд 22ПРИМЕНЕНИЕ
Распределение регистров
Компилятор — это компьютерная программа, которая переводит
один компьютерный язык в другой. Для улучшения времени выполнения результирующего
кода одной из техник компиляторной оптимизации является распределение регистров, в которой наиболее часто используемые переменные компилируемой программы хранятся в быстродействующих регистрах процессора. В идеальном случае переменные хранятся в регистрах так, что они все находятся в регистрах во время их использования.Компилятор строит интерференционный граф, где вершины соответствуют регистрам, а ребра соединяют две из них, если они нужны в один и тот же момент времени
Цифровые водяные знаки
Технология цифровых водяных знаков (англ. digital watermarking) позволяет вместе с данными (будь то медиафайлы, исполняемые файлы и прочие) передать некое скрытое сообщение («водяной знак», Watermark). Такое скрытое сообщение может быть применено в защите авторских прав для идентификации владельца данных.
Слайд 23ЗАДАЧА СОСТАВЛЕНИЯ РАСПИСАНИЯ
В студенческих группах 26-К и 28-К надо провести
занятия по
А) операционным системам;
Д) Дискретной математике и теории
графов, М) Математической логике и
И) Истории
(по одному занятию по каждому предмету).
Занятия по каждому предмету проводятся с каждой группой отдельно.
Занятия по операционным системам и по теории графов ведет преподаватель X, по математической логике – преподаватель Y , по истории – преподаватель Z.
Найти минимальное число пар, в которые можно «уложить» все занятия, и составить соответствующее расписание.
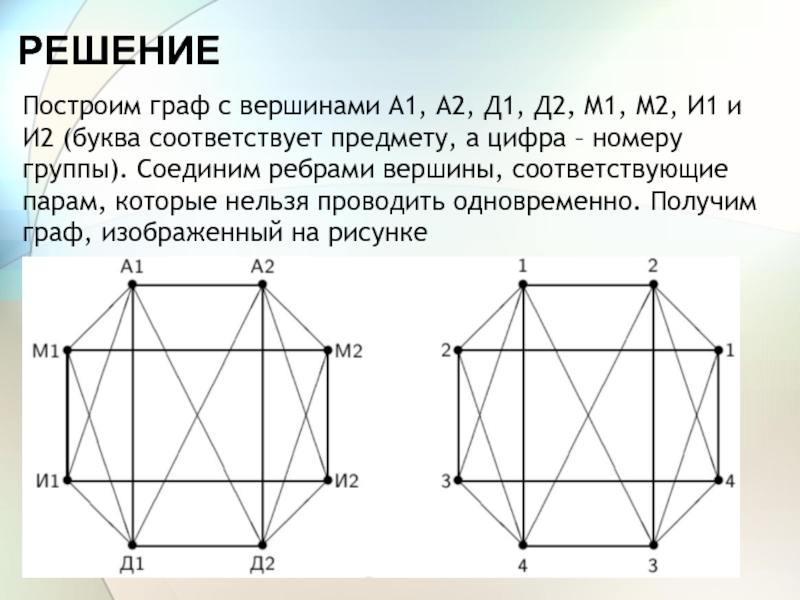
Слайд 24РЕШЕНИЕ
Построим граф с вершинами А1, А2, Д1, Д2, М1, М2,
И1 и И2 (буква соответствует предмету, а цифра – номеру
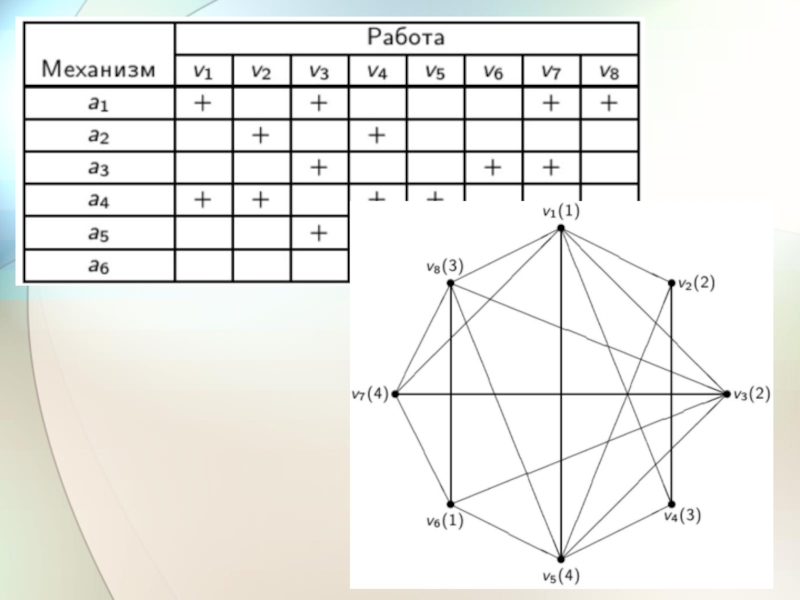
группы). Соединим ребрами вершины, соответствующие парам, которые нельзя проводить одновременно. Получим граф, изображенный на рисункеСлайд 25ЗАДАЧА РАСПРЕДЕЛЕНИЯ ОБОРУДОВАНИЯ
Имеется некоторое количество работ и механизмов для их
осуществления. Для выполнения каждой работы требуется одно и то же
время. При этом никакой из механизмов не может быть занят одновременно более чем в одной работе. Нужно распределить механизмы так, чтобы общее время выполнения работ было минимально возможнымДля перевода этой задачи на язык теории графов рассмотрим граф G, вершинами которого являются работы, причем две различные вершины смежны тогда и только тогда, когда для выполнения соответствующих работ требуется хотя бы один общий механизм
Слайд 27АЛГОРИТМ РАСКРАСКИ
1. Упорядочить вершины по невозрастанию степени.
2. Окрасить первую
вершину в цвет 1.
3. Выбрать цвет окраски 1.
4.
Пока не окрашены все вершины, повторять п.4.1.-4.2.: 4.1. Окрасить в выбранный цвет всякую вершину, которая не смежна с другой, уже окрашенной в этот цвет.
4.2. Выбрать следущий цвет.