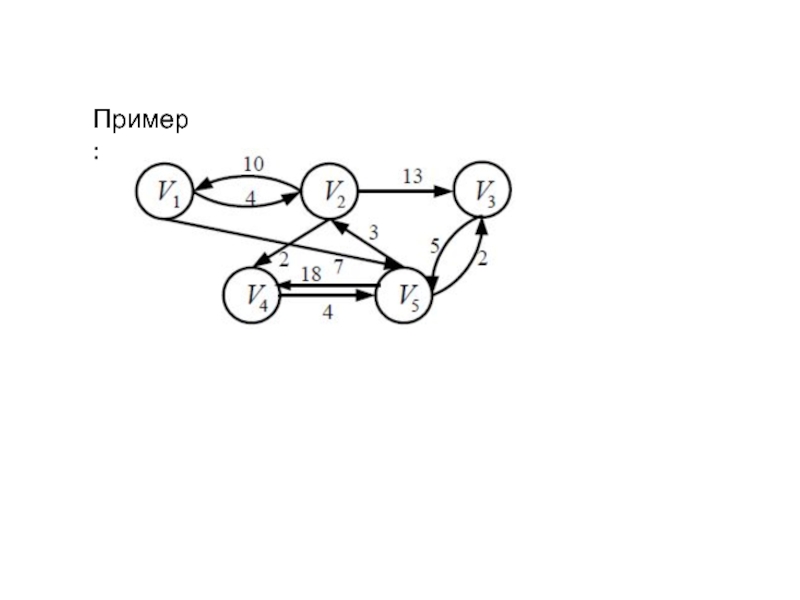
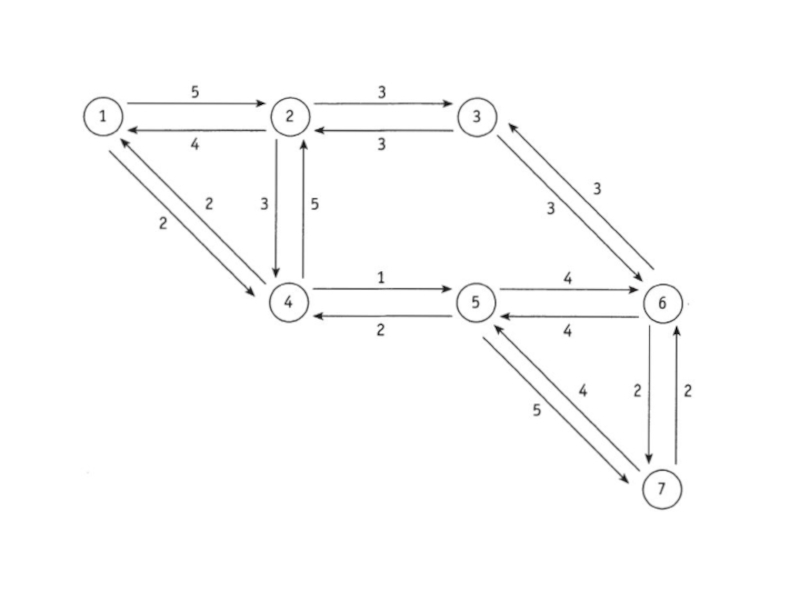
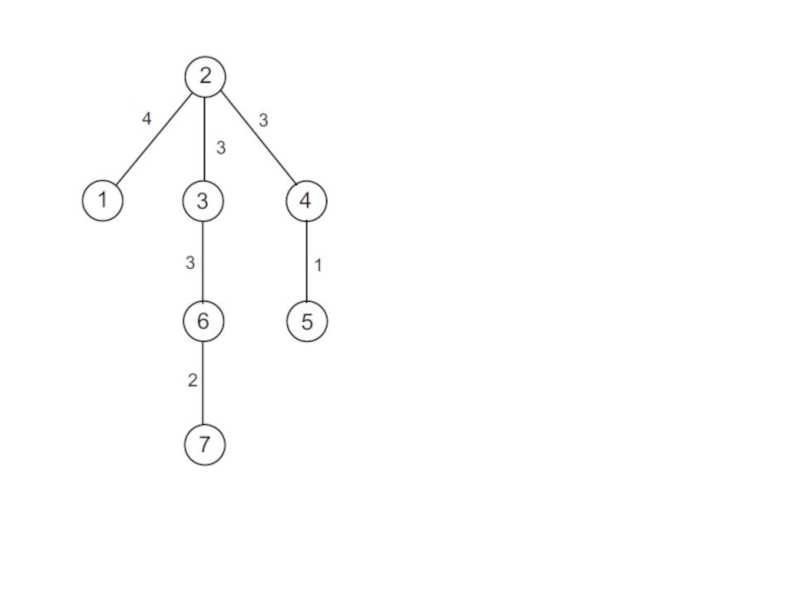
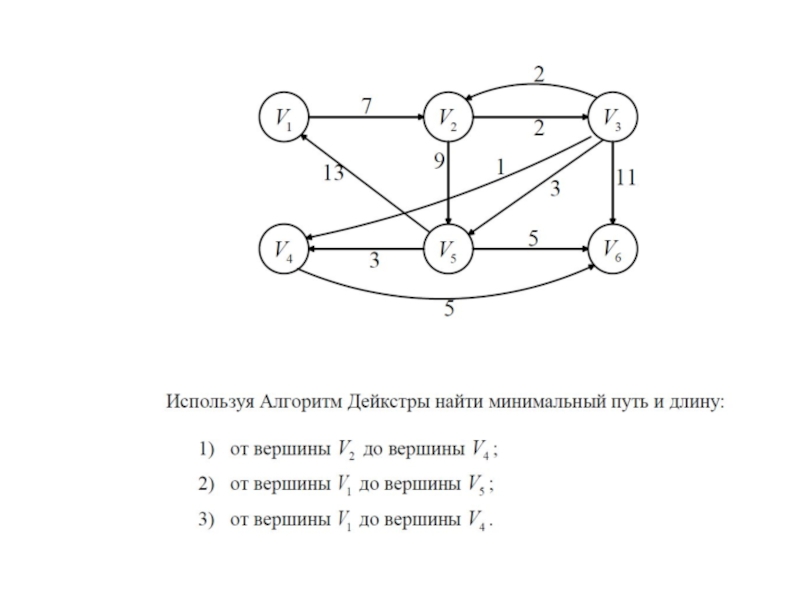
С длин дуг.
Выход: матрица Т длин путей и матрица
H самих путей.for г from 1 to p do
for j from 1 to p do
T[i,j] = C[i,j] { инициализация }
if C[i,j] = ∞ then H[i, j] = 0 { нет дуги из i в j }
else H[i,j]: =j
end
end



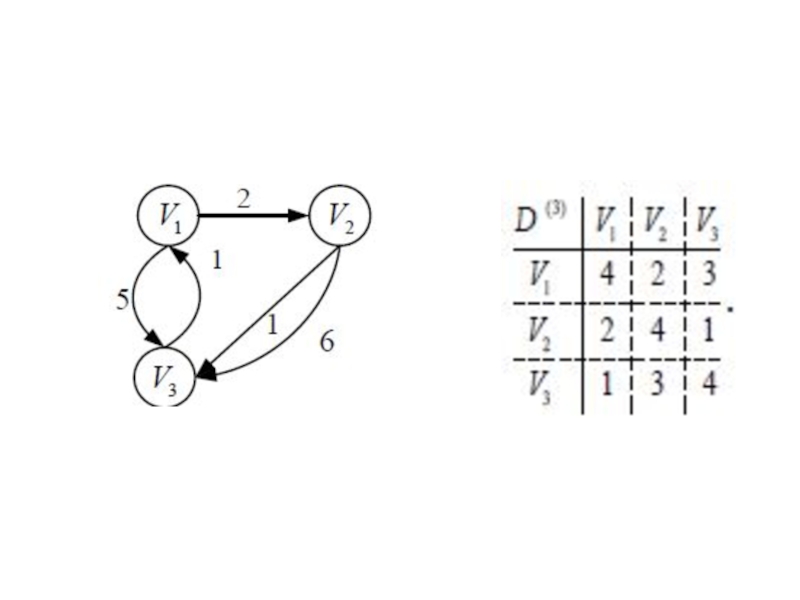

![Поиск пути наименьшей длины H[s]: = 0; T[s]: = 0; X [s] = 1 v H[s]: = 0; T[s]: = 0; X [s] = 1 v = s { текущая вершина }](/img/thumbs/14c7e69e740f746dc7d69a47d1ed7d32-800x.jpg)