Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Полный момент импульса электрона в атоме. Символические обозначения термов. Правила отбора для оптических переходов.
Содержание
- 1. Полный момент импульса электрона в атоме. Символические обозначения термов. Правила отбора для оптических переходов.
- 2. Операции с векторами L и S можно
- 3. Во-вторых, полный момент J, как всякий момент
- 4. Проекция вектора J на какое либо направление
- 5. Эти правила сложения векторов L и S
- 6. Различные состояния атома (термы) принято обо-значать специальными
- 7. Т.к. терм - это характеристика всего атома,
- 8. Правила отбора для оптических переходовСогласно комбинационному принципу,
- 9. Эти правила связаны с законами сохранения мо-мента
- 10. Если условие (17.10) соблюдается, то такие пере-ходы
- 11. Вероятность перехода определяется так называ-емым матричным элементом:
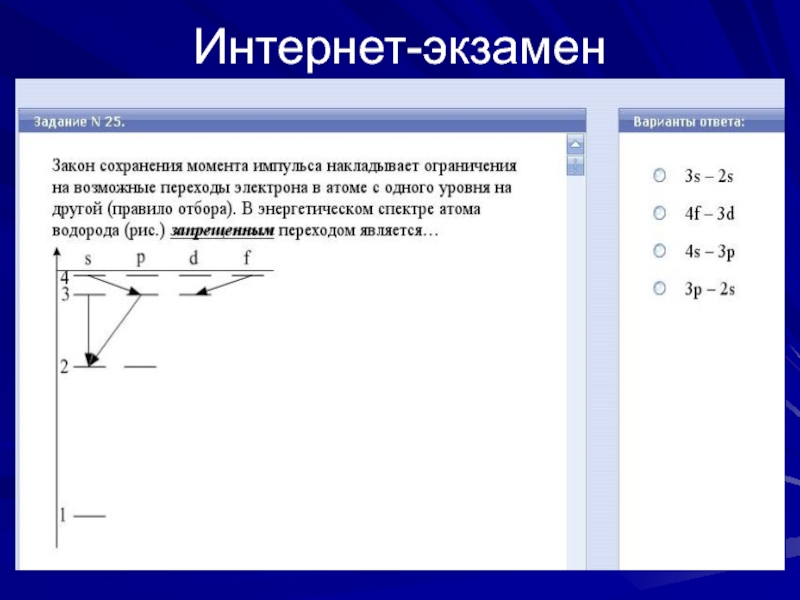
- 12. Интернет-экзамен
- 13. Интернет-экзамен
- 14. Скачать презентанцию
Операции с векторами L и S можно производить с помощью следующего полуклассического мето-да. Вектора складываются по обычным прави-лам параллелограмма:J = L + S,
Слайды и текст этой презентации
Слайд 2Операции с векторами L и S можно производить с помощью
следующего полуклассического мето-да. Вектора складываются по обычным прави-лам параллелограмма:
J =
L + S, (17.1)в результате получается вектор J - вектор полно-го момента импульса. В это чисто классическое правило вносятся следующие поправки, харак-терные для квантовой механики. Во-первых, уг-лы между векторами L и S не могут быть произ-вольными. Вектор L может располагаться отно-сительно вектора J только под такими углами, чтобы его проекция на направление J была ра-вна , где m = 0, ± 1, …, ± l. Аналогичное тре-бование предъявляется и к ориентации вектора S: его проекция на направление J равна , где ms = ±1/2. Таким образом, угол между L и S может принимать ряд дискретных значений.
Слайд 3Во-вторых, полный момент J, как всякий момент импульса в квантовой
механике имеет свое квантовое число j, такое, что
(17.2)
Число j называется
внутренним квантовым чис-лом, оно может принимать значения:(17.3)
Формула (17.3) записана в общем виде для любой величины вектора S. Если рассматривается всего один электрон, то s =1/2, и тогда j может принимать всего два значения:
и (17.4)
Слайд 4Проекция вектора J на какое либо направление Z (ось квантования,
направление внешнего маг-нитного или электрического поля и т.д.) в соот-ветствии
с законами квантовой механики равна:, (17.5)
где (17.6)
т.е. mj может принимать (2j + 1) значений. Число mj называется магнитным внутренним кван-товым числом. Если j - полуцелое число, то в этом случае mj не принимает значение 0.
Слайд 5Эти правила сложения векторов L и S со-ставляют векторную модель
атома, имеющую большое практическое значе-ние: модель проста и наглядна, а
ее ре-зультаты совпадают с экспериментом и с результатами точного квантовомехани-ческого решения.
Слайд 6Различные состояния атома (термы) принято обо-значать специальными символами, по которым
сразу можно указать все квантовые числа. Об-щий вид такого обозначения:
(17.7)
где
квантовое число L обозначает орбитальный момент всего атома (так же, как и для отдельно-го электрона): L = 0 1 2 3 4 …Символ S P D F G …
Справа внизу записывается квантовое число пол-ного момента атома, слева вверху – кратность (мультиплетность) терма:
(17.8)
где S – спиновое квантовое число всего атома.
Слайд 7Т.к. терм - это характеристика всего атома, то ис-пользуются прописные
буквы вместо строчных (которые применяются для отдельного электро-на). Примеры:
Запись
(читается "дублет Р три вторых") означает, что L = 1, S = 1/2, J = 3/2.Запись (читается "синглет S ноль") озна-чает, что L = 0, S = 0, J = 0.
Запись (читается "триплет D два") означа-ет, что L = 2, S = 1, J = 2.
Слайд 8Правила отбора для оптических переходов
Согласно комбинационному принципу, волновое число любой
спектральной линии (в испускании и поглощении) может быть представлена как
разность двух термов(17.9)
Но обратное утверждение не всегда справедливо: не всякая комбинация термов дает частоту, со-ответствующую реально наблюдаемой спект-ральной линии. Существуют определенные пра-вила отбора, указывающие, какие комбинации термов возможны, какие нет (точнее маловеро-ятны или даже имеют нулевую вероятность).
Слайд 9Эти правила связаны с законами сохранения мо-мента импульса и четности
в квантовых пере-ходах. В частности установлено, что в атоме наиболее
вероятны переходы между состояни-ями, при которых квантовые числа l и m меня-ются на величину:(17.10)
причем правило отбора для магнитного квантово-го числа m надо учитывать только в том слу-чае, если атом находится в магнитном поле. На главные квантовые числа n1 и n2 никаких огра-ничений не накладывается, т.е. величина ∆n может быть любой.
Слайд 10Если условие (17.10) соблюдается, то такие пере-ходы называются разрешенными. Другие
пере-ходы маловероятны, и их называют запрещен-ными. Другими словами, разрешены переходы
между соседними по l уровнями, т.е. между s- и p-состояниями, между p- и d-состояниями, меж-ду d- и f-состояниями и т.д.Интенсивность спектральной линии определяется вероятностью перехода электрона из одного со-стояния в другое. В теории Бора это можно бы-ло представить наглядно в виде пространствен-ного перемещения электрона с одной орбиты на другую. В квантовой теории никаких орбит нет, а переход связан с представлением об изменении волновой функции.