Слайд 1
Portfolio Construction
Mikhail Kamrotov
Data Analysis in Economics and Finance
Слайд 2Satisfying vs optimal
Simple rules are often far more robust than
complicated ”optimal” alternatives
Rules of thumb work surprisingly well in a
variety of fields (Haldane, 2012)
Reasons:
“collecting and processing the information necessary for complex decision-making is costly”
“fully defining future states of the world, and probability‑weighting them, is beyond anyone’s cognitive limits”
Oversimplifying things is obviously bad as well
Слайд 3Simplicity in portfolio theory
“One should always divide his wealth into
three parts: a third in land, a third in merchandise,
and a third ready to hand.”
Source: Rabbi Isaac bar Aha, Babylonian Talmud: Tractate Baba Mezi’a, folio 42a, 4th century
Empirically valid statement
Naïve, equal-weight portfolio frequently delivers better results than “optimal” allocation strategies (DeMiguel, 2005)
Let’s test this simple allocation strategy!
Слайд 4Steps of strategy evaluation
Formally define rules for decision-making
Collect data and
clean it
Simulate trading process
Compare the results to the benchmark
Compute performance
metrics
Слайд 5Decision-making rules
Distribute the initial capital equally between N stocks
Example:
Initial capital:
$1000
10 stocks
You invest $100 in each stock and stay away
from the market for a while
Looks simple!
Слайд 6Not so simple in fact
How to choose N stocks (assets)
to invest in?
Infinite possible solutions:
All US stocks
All stocks in the
world
All stocks, bonds, currencies, real estate – everything
Only stocks that satisfy specific conditions (most liquid stocks, stocks of the largest companies, stocks with low P/E ratio, etc.)
Result crucially depends on the answer
Universe of securities is a set of stocks (assets) you’re focusing on
Слайд 7Universe of securities
We will look at largest US companies by
market capitalization
Capitalization = Number of shares * Price of one
share
Components of Russell 1000
Pay attention to the methodology of index (sections 6.1.1 and 6.10.1 in Russell_methodology.pdf)
Russell 1000 defines universe of ~1000 largest US companies
They account for ~90% of total market capitalization
You can try S&P 500 and DJIA as well, or apply any custom filter: dividends, P/E, most volatile stocks, etc.
Слайд 8Data collection
We need daily close prices for all Russell 1000
components
Yahoo! Finance is one of the options
Yahoo! close prices are
now split adjusted
Split example:
In June 2014 Apple shares were at ~$700 per share
A 7-to-1 split was implemented by Apple in June
Each stock you owned turned into 7 stocks and the price went down to ~$100
Split adjusted prices mean that all prices before the split are divided by 7
Слайд 10Compare result with the benchmark
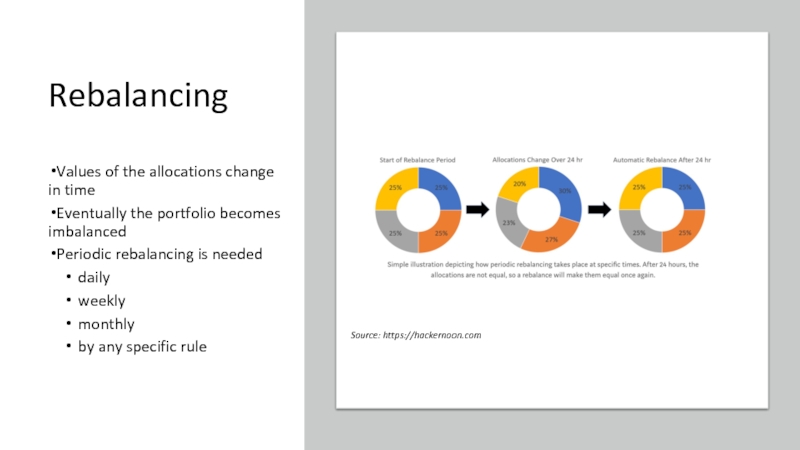
Слайд 11Rebalancing
Values of the allocations change in time
Eventually the portfolio becomes
imbalanced
Periodic rebalancing is needed
daily
weekly
monthly
by any specific rule
Source: https://hackernoon.com
Слайд 12Backtest pitfalls
Survivorship bias
we picked only companies that didn’t go bankrupt
moreover,
they were eventually included in Russell 1000 – we picked
the best ones
No trading costs
Trading on close prices is impossible
Stocks are not sold in fractions
See “A Practitioner’s Guide to Assessing Strategies and Avoiding Pitfalls” and chapter 3 of “Successful Algorithmic Trading” (M. Halls-Moore, 2015) for advanced details
Слайд 13Measures of risk and return
Mean
Variance
Standard deviation
Covariance
Correlation
Слайд 15Covariance and correlation
Diversification implies distributing investments between different assets
“Don’t put
all your eggs in one basket”
Investing in 1000 similar stocks
does not spread your risks
Covariance and correlation measure relationship between variables (assets)
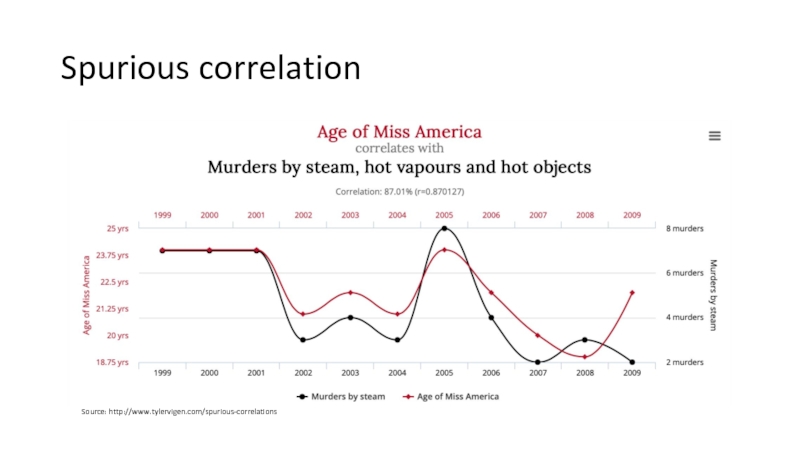
Слайд 18Spurious correlation
Source: http://www.tylervigen.com/spurious-correlations
Слайд 19Covariance matrix
Is used to construct a diversified portfolio
Shows covariances for
all possible pairs of assets
Covariance matrix is symmetric
The diagonal elements
contain the variances
R automatically computes covariance matrix, when cov() is applied to a matrix or a data frame