Постановка задачи о радиальном распределении температуры в облучательном устройстве при отсутствии утечек тепла в торцы

температуры в облучательном устройстве при отсутствии утечек тепла в торцы.

Обратить внимание на то, что для этого случая можно получить аналитическое решение, пригодное для оценочных расчетов радиального поля температуры по элементам облучательного устройства, тепловой изоляции или определения местоположения и мощности нагревателя для создания нужного температурного режима на облучаемом образце.

План.
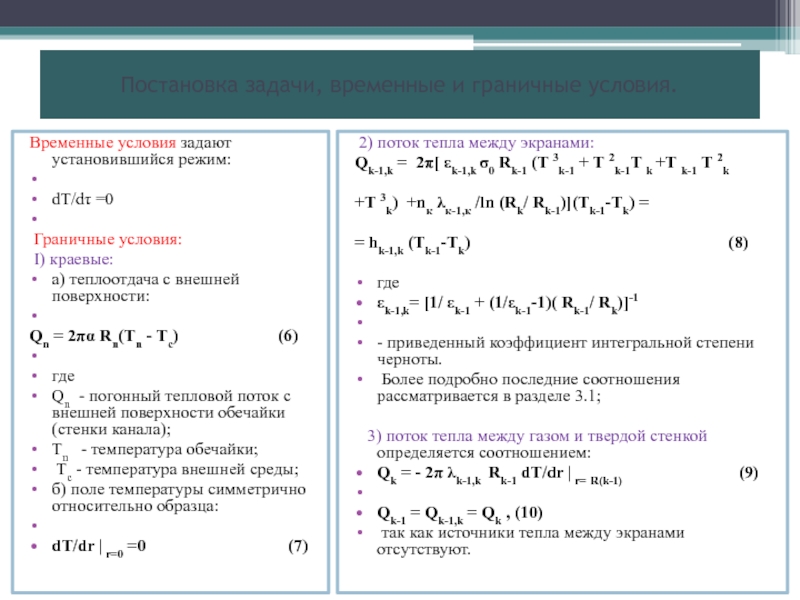
1. Постановка задачи о радиальном распределении температуры в облучательном устройстве при отсутствии утечек тепла в торцы.
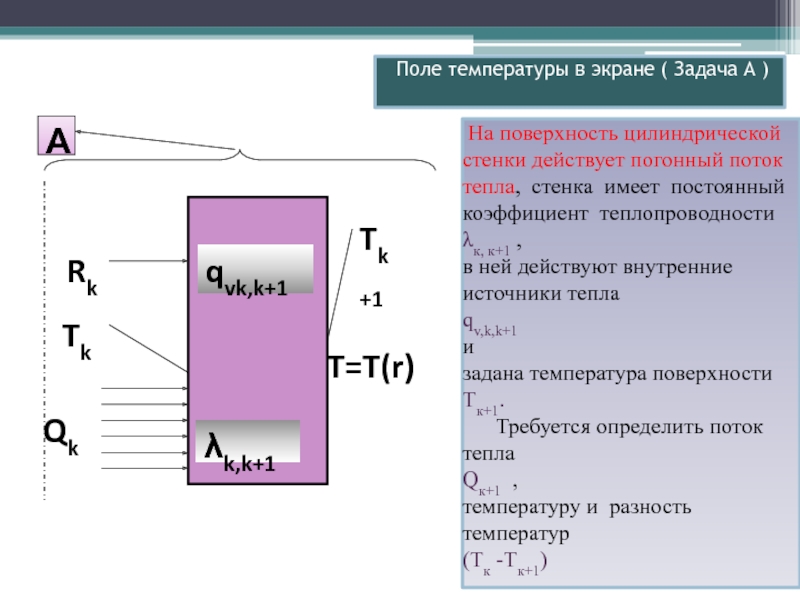
2. Постановка и решение вспомогательной задачи (А).
 
 

 

в торцы.
Рассмотренная в предыдущем разделе задача реализуется

с помощью ЭВМ, дает пространственное распределение поля температуры для осе симметричной геометрии облучательного устройства, однако, неоправданно сложна, если необходимо оценить тепловую изоляцию или мощность и местоположение нагревателя для создания нужного температурного режима на облучаемом образце.
Рассмотрим задачу о радиальном распределении температуры в облучательном устройстве при отсутствии утечек тепла в торцы.

экранами с радиусами R k , R k+1 . Последний

экран R n является обечайкой установки или стенкой канала.
Экраны и образец по длине настолько велики, что влиянием теплоотвода в торцы можно пренебречь.

Радиальное распределение температуры в облучательном устройстве при отсутствии утечек тепла в торцы.

и обечайку установки с теплопроводностью λ = const при

расчете поля температуры внутри элемента, но λ =f (Т) при рассмотрении задачи в целом. В образце, экранах и обечайке (стенке канала) действуют внутренние источники тепла q V,k,k +1 (Bт/см3). Любой из экранов может быть нагревателем, и тогда его источники тепла можно выразить:
 
q V k,k+1= q V k,k+1,р + q V k,k+1, э
 
q V k,k+1,р - внутренние источники тепла при действии радиации;
q V k,k+1,э = j2 R - внутренние источники тепла при действии электрического тока, где j -плотность электрического тока (А/см3 ), ρ - удельное электросопротивление (Ом. cм).

газом с коэффициентом теплопроводности λк-1,к , который постоянен при рассмотрении

теплопередачи между экранами и зависит от температуры при рассмотрении общей задачи.
вакуумировано,
источники тепла между экранами отсутствуют q V k-1,k= 0.
Заданы:
- интегральные степени черноты экранов.
- температура окружающей среда Tс и α.
Процесс передачи тепла осуществляется:
- между экранами: излучением, теплопроводностью и конвекцией;
- в экранах - теплопроводностью;
- с внешней поверхности обечайки с коэффициентом теплоотдачи α.

теплоотдача с внешней поверхности:

Qn = 2πα Rn(Тn - Тc)

(6)
 
где
Qn - погонный тепловой поток с внешней поверхности обечайки (стенки канала);
Тn - температура обечайки;
Тс - темпе­ратура внешней среды;
б) поле температуры симметрично относительно образца:
 
dT/dr | r=0 =0 (7)

2) поток тепла между экранами:
Qk-1,k = 2π[ εk-1,k σ0 Rk-1 (Т 3k-1 + Т 2k-1Т k +Т k-1 Т 2k

+Т 3k) +nк λк-1,к /ln (Rk/ Rk-1)](Тk-1-Tk) =

= hk-1,k (Тk-1-Tk) (8)
 
где
εk-1,k= [1/ εk-1 + (1/εk-1-1)( Rk-1/ Rk)]-1
 
- приведенный коэффициент интегральной степени черноты.
 Более подробно последние соотношения рассматривается в разделе 3.1;

3) поток тепла между газом и твердой стенкой определяется соотношением:
Qk = - 2π λk-1,k Rk-1 dT/dr | r= R(k-1) (9)
 
Qk-1 = Qk-1,k = Qk , (10)
 так как источники тепла между экранами отсутствуют.

Постановка задачи, временные и граничные условия.

позволяют определить потоки тепла Qk для
каждого значения rк

в том числе и для rn – Qn ;
2. По значению Qn можно определить температуру поверхности обечайки и далее температуру поверхности Тn-1 , решив задачу теплопроводности;
3. Зная условия теплообмена между экранами и поток Qn , можно найти Тn-2 , а из решения задачи теплопроводности определить
Тn-3 и т.д.;
4. Следует помнить, что полученные значения Ti будут первыми приближениями, так как условия теплообмена между экранами зависят от Ti и поэтому точное решение получают методом последовательных приближений.
5.Для решения задачи предварительно необходимо рассмотреть поле температуры в экране и образце.

поверхность цилиндрической стенки действует погонный поток тепла, стенка имеет постоянный

коэффициент теплопроводности λк, к+1 ,
в ней действуют внутренние источники тепла
qv,k,k+1
и
задана температура поверхности Tк+1.
Требуется определить поток тепла
Qк+1 ,
температуру и разность температур
(Tк -Tк+1)

2π λk,k+1 Rk (dT/dr | r= Rk )

(11) ,
 
T| r=Rk+1 = Тk+1 (12)
 
Поле температуры описывается уравнением:
 
d2T/dr2 + (1/r) ( dT/dr) + qv,k,k+1/ λк, к+1 = 0 (13)
 
Решение уравнения имеет вид:
 
T= - (r2 /4) qv,k,k+1/ λк, к+1 +C1ln r +C2 (14)

следующем виде:
 
Т = Тk+1 + qv,k,k+1/2 λк, к+1[(R2k+1 – r2)/2

– R2kln(Rk+1/r) ] +
 
(Qk/2 πλк, к+1) ln(Rk+1/r) (15)
 
Тk - Тk+1 = (qv,k,k+1/2 λк, к+1)[(R2k+1 – R2k)/2 – R2kln(Rk+1/ Rk) ] +
 
(Qk/2 πλк, к+1) ln(Rk+1/ Rk) (16)
 
Qk+1 = - 2π λk,k+1 Rk+1 dT/dr | r= Rk+1= πqv,k,k+1(R2k+1 – R2k) + Qk (17)
 
Тk - Тk+1 = Av,k,k+1+ Ak,k+1 (18)

Решение задачи А.