Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Числа Фибоначчи
Содержание
- 1. Числа Фибоначчи
- 2. ФИБОНАЧЧИ (ок. 1175–1250)Итальянский математик. Родился в Пизе,
- 3. История. Последовательность Фибоначчи была хорошо известна в
- 4. На Западе эта последовательность была исследована Леонардо
- 5. Слайд 5
- 6. ЧИСЛА ФИБОНАЧЧИ - числовая последовательность, где каждый
- 7. Слайд 7
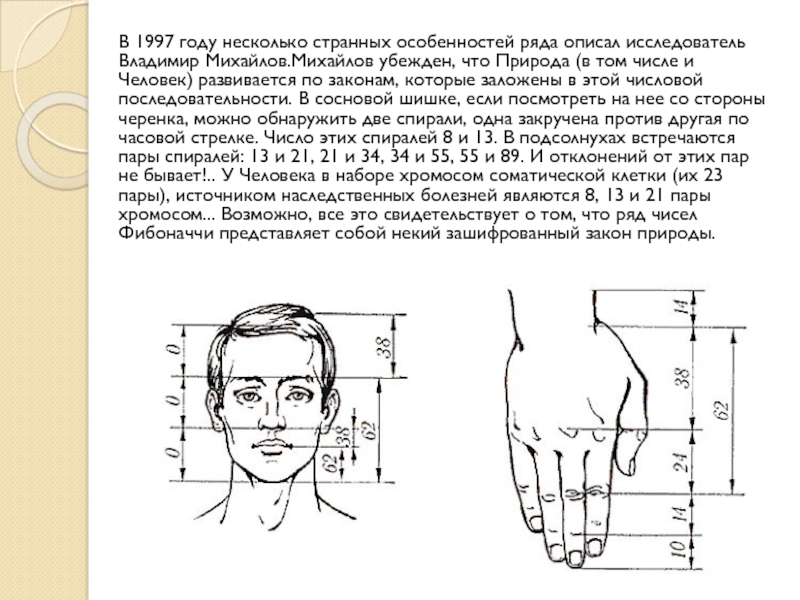
- 8. В 1997 году несколько странных особенностей ряда
- 9. Цифровой код развития цивилизации можно определить с
- 10. Используемые источники для создания презентации:http://ru.wikipedia.org/wiki/Числа_Фибоначчиhttp://www.bibliotekar.ru/index.files/1/315.htmhttp://elementy.ru/trefil/21136
- 11. Спасибо за внимание.
- 12. Скачать презентанцию
ФИБОНАЧЧИ (ок. 1175–1250)Итальянский математик. Родился в Пизе, стал первым великим математиком Европы Средневековья. Он издавал свои книги по арифметике, алгебре и другим математическим дисциплинам. От мусульманских математиков он узнал о системе
Слайды и текст этой презентации
Слайд 1Презентация на тему:
Числа Фибоначчи
«Школа №1195»
Подготовил ученик
10 класса «У» Мацукевич Валерий
Борисович
Слайд 2ФИБОНАЧЧИ
(ок. 1175–1250)
Итальянский математик. Родился в Пизе, стал первым великим
математиком Европы Средневековья. Он издавал свои книги по арифметике, алгебре
и другим математическим дисциплинам. От мусульманских математиков он узнал о системе цифр, придуманной в Индии и уже принятой в арабском мире, и уверился в ее превосходстве (эти цифры были предшественниками современных арабских цифр).Слайд 3История.
Последовательность Фибоначчи была хорошо известна в древней Индии
Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу
длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».Слайд 4На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи,
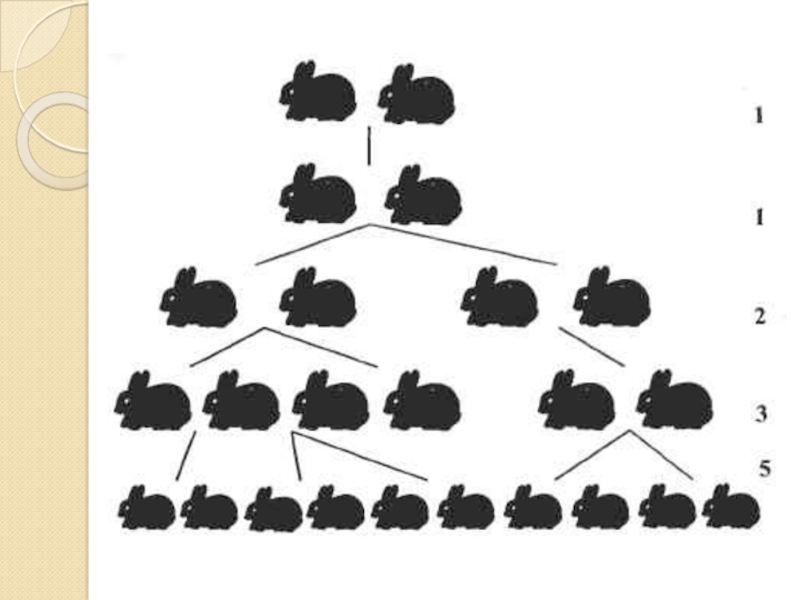
в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной
(биологически нереальной) популяции кроликов, предполагая что:В «нулевом» месяце имеется пара кроликов (1 новая пара).
В первом месяце первая пара производит на свет другую пару (1 новая пара).
Во втором месяце обе пары кроликов порождают другие пары и первая пара погибает (2 новые пары).
В третьем месяце вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (3 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.
Пусть популяция за месяц n будет равна Fn . В это время только те кролики, которые жили в месяце n-2 , являются способными к размножению и производят потомков, тогда Fn-2 пар прибавится к текущей популяции Fn-1. Таким образом общее количество пар будет равно: Fn = Fn-2 + Fn-1.
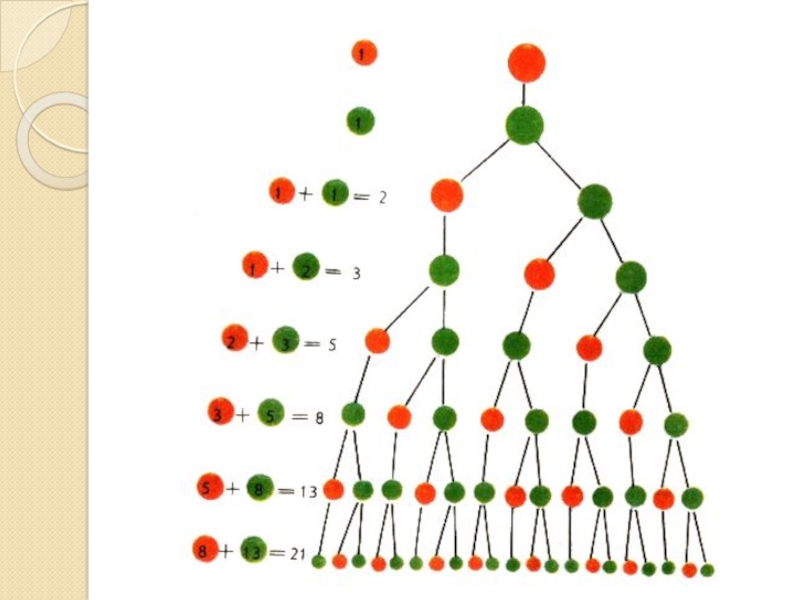
Слайд 6ЧИСЛА ФИБОНАЧЧИ - числовая последовательность, где каждый последующий член ряда
равен сумме двух предыдущих, то есть: 1, 1, 2, 3,
5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368,.. 75025,.. 3478759200, 5628750625,.. 260993908980000,..422297015649625,.. 19581068021641812000,..Изучением сложных и удивительных свойств чисел ряда Фибоначчи занимались самые различные профессиональные ученые