Поверхностные модели построенные по кинематическому принципу

Содержание

1. Поверхностные модели построенные по кинематическому принципу
2. Поверхность вращения Может быть построена в
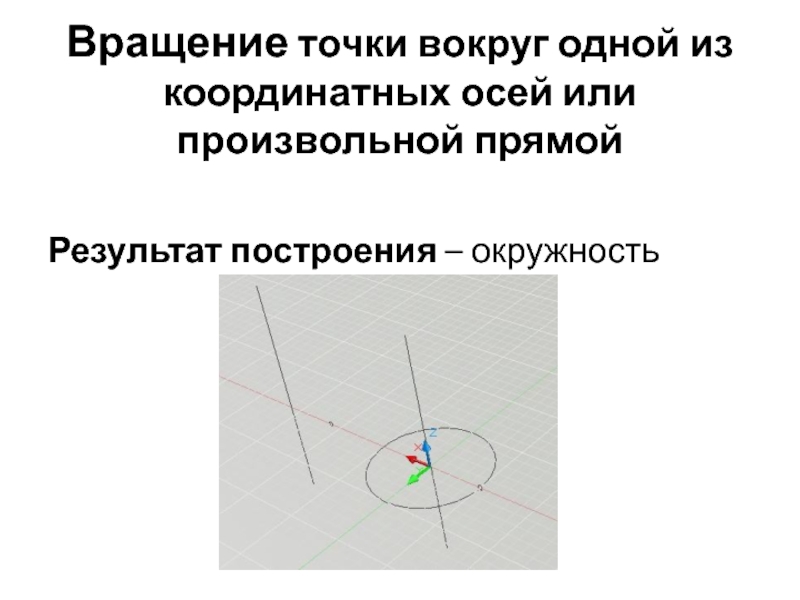
3. Вращение точки вокруг одной из координатных осей или произвольной прямой Результат построения – окружность
4. Отрезок и ось вращения компланарны и
5. Отрезок и ось вращения компланарны ,
6. Отрезок и ось вращения компланарны, отрезок перпендикулярен
7. Отрезок и ось вращения не компланарны Результат построения - однополосный гиперболоид
8. Вращение половины окружности вокруг оси, лежащей в
9. Вращение половины эллипса вокруг оси, лежащей
10. Вращение окружности вокруг оси, лежащей с ней
11. Математические основы построения поверхности вращения Поверхность
12. Рассмотрим математическое описание поверхности вращения вокруг оси
13. Данное математическое выражение поверхности вращения можно представить в матричном виде следующим образом.
14. Поворот относительно оси, не совпадающей ни с
15. Скачать презентанцию

Поверхность вращения Может быть построена в результате вращения двумерного объекта (прямая, плоская кривая) вокруг оси в пространстве Рассмотрим основные типы геометрических моделей, построенных на основе вращения

Главная
Разное
Поверхностные модели построенные по кинематическому принципу

Слайды и текст этой презентации

Слайд 1Поверхностные модели построенные по кинематическому принципу
Поверхность вращения
Поверхность соединения – линейчатая

поверхность
Поверхность перемещения – заметающая поверхность,sweep и lofting поверхности

Поверхностные модели построенные по кинематическому принципуПоверхность вращенияПоверхность соединения – линейчатая поверхностьПоверхность перемещения – заметающая поверхность,sweep и lofting

Слайд 2Поверхность вращения
Может быть построена в результате вращения двумерного

объекта (прямая, плоская кривая) вокруг оси в пространстве
Рассмотрим

основные типы геометрических моделей, построенных на основе вращения

Поверхность вращения Может быть построена в результате вращения двумерного объекта (прямая, плоская кривая) вокруг оси в

Слайд 3Вращение точки вокруг одной из координатных осей или произвольной прямой
Результат

построения – окружность

Слайд 4Отрезок и ось вращения компланарны и параллельны друг другу
Результат построения

– цилиндрическая поверхность или твердотельный цилиндр

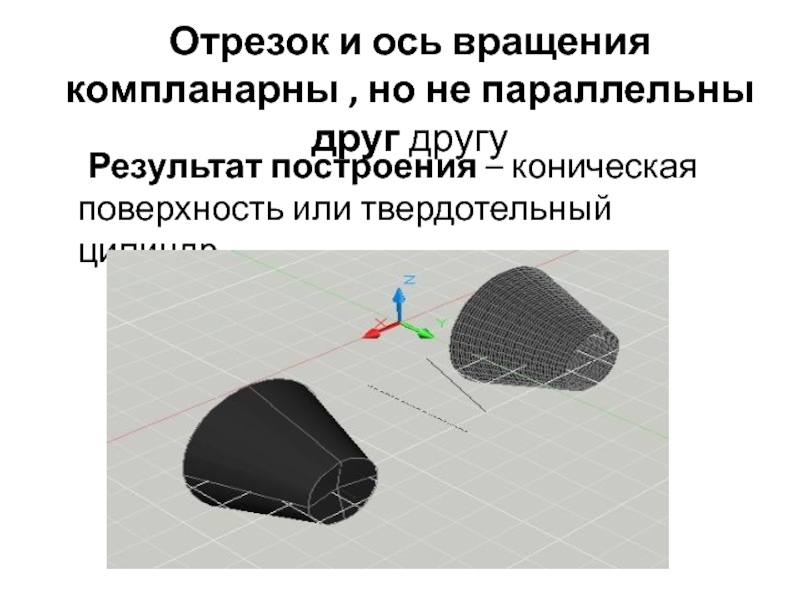
Слайд 5 Отрезок и ось вращения компланарны , но не параллельны друг

другу
Результат построения – коническая поверхность или твердотельный

цилиндр

Отрезок и ось вращения компланарны , но не параллельны друг другу Результат построения

Слайд 6Отрезок и ось вращения компланарны, отрезок перпендикулярен оси вращения
Результат построения:
Плоский

диск, если отрезок
доходит до оси вращения

Диск с

отверстием если диск
не доходит до оси вращения

Отрезок и ось вращения компланарны, отрезок перпендикулярен оси вращенияРезультат построения:Плоский диск, если отрезок доходит до

Слайд 7Отрезок и ось вращения не компланарны
Результат построения -

однополосный гиперболоид

Слайд 8Вращение половины окружности вокруг оси, лежащей в той же плоскости

и проходящей через ее центр.
Результат построения – поверхностная или твердотельная

сфера

Вращение половины окружности вокруг оси, лежащей в той же плоскости и проходящей через ее центр. Результат построения

Слайд 9 Вращение половины эллипса вокруг оси, лежащей в той же плоскости

и совпадающей с одной из его осей
Результат построения – поверхностный

или твердотельный эллипс

Вращение половины эллипса вокруг оси, лежащей в той же плоскости и совпадающей с одной из его

Слайд 10Вращение окружности вокруг оси, лежащей с ней в одной плоскости

и не пересекающей ее
Результат построения - поверхностный или твердотельный тор

Вращение окружности вокруг оси, лежащей с ней в одной плоскости и не пересекающей ееРезультат построения - поверхностный

Слайд 11Математические основы построения поверхности вращения
Поверхность вращения помимо самостоятельной

трехмерной поверхностной модели может быть основой для построения оболочки твердого

тела.
Точки на поверхности задаются тремя координатами, каждая из которых является функцией параметра t: p(t)=[x(t),y(t),z(t)]
В общем виде функция Q(t,q), описывающая поверхность вращения, зависит от двух переменных: параметра t и угла поворота q.

Математические основы построения поверхности вращения Поверхность вращения помимо самостоятельной трехмерной поверхностной модели может быть основой для

Слайд 12Рассмотрим математическое описание поверхности вращения вокруг оси X.
Q(t,q)=[x(t), y(t)cos(q),y(t)sin(q)]

Пояснения к данному выражению даны на

на рисунке.

Рассмотрим математическое описание поверхности вращения вокруг оси X. Q(t,q)=[x(t), y(t)cos(q),y(t)sin(q)] Пояснения к данному выражению даны

Слайд 13Данное математическое выражение поверхности вращения можно представить в матричном виде

следующим образом.

Слайд 14Поворот относительно оси, не совпадающей ни с одной из координатных

осей
Решение задачи путем сведения ее к более простой –

поворот относительно одной из координатных осей (например с осью X).
Для этого необходимо выполнить следующие преобразования:
Перенос точки на оси в начало координат
Выполнить необходимые повороты для совмещения оси с осью Z.
Повернуть вокруг оси y на уголь900 для совмещения исходной оси с осью X.
Выполнить поворот относительно оси X
Выполнить обратные преобразовангия

Поворот относительно оси, не совпадающей ни с одной из координатных осей Решение задачи путем сведения ее к

Скачать презентацию