Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Практическое занятие №1 по дисцеплине Криптографические методы защиты
Содержание
- 1. Практическое занятие №1 по дисцеплине Криптографические методы защиты
- 2. История криптографии насчитывает около 4 тысяч лет.
- 3. АтбашДаже в Библии можно найти примеры шифровок,
- 4. Шифр моноалфавитной подстановки – это один из
- 5. Простейшим примером моноалфавитных подстановок является шифр Цезаря.
- 6. Какой-то хитрец из спартанцев обнаружил, что если
- 7. Для прочтения шифровки нужно не только знать
- 8. Квадрат ПолибияДревней Греции (П в. до н.
- 9. Существует еще один вариант шифрования при помощи
- 10. Шифр четырех квадратовСтроят 4 квадрата размера 5х5
- 11. Становление науки криптологии Мы истину, похожую на
- 12. Ручные шифры Средневековья НЕЯСНОЕ СТАНОВИТСЯ ЕЩЕ БОЛЕЕ
- 13. Перестановка колонок по ключудо перестановкипосле перестановки СНЯНН
- 14. Двойные перестановки Исходная таблица Перестановка столбцовПерестановка строкАЗЮЖЕ
- 15. Магический квадрат Альбрехт ДюрерНа известной гравюре Дюрера
- 16. Магический, или волшебный квадрат — это квадратная
- 17. Подобные квадраты широко применялись для вписывания шифруемого
- 18. Шифры замены цифр на буквы Собственно, это
- 19. Шифр Гронсфельда Состоит в модификации шифра Цезаря
- 20. Шифрующие таблицы Многие историки считают Иоганна Трисемуса,
- 21. Биграмные шифры Трисемус первым заметил, что можно
- 22. Трафаретные шрифтыВписывание в прорезанные ячейки текста и
- 23. Практическая частьЗашифруйте свое ФИО с помощью:атбаш;шифра Цезаря
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Кафедра "ИБ"
Практическое занятие №1
по дисцеплине «Криптографические методы защиты информации»
Тема
:Элементарные шифры.
Слайд 2История криптографии насчитывает около 4 тысяч лет. В качестве основного
критерия периодизации криптографии возможно использовать технологические характеристики используемых методов шифрования.
Первый
период (приблизительно с 3-го тысячелетия до н. э.) характеризуется господством моноалфавитных шифров (основной принцип – замена алфавита исходного текста другим алфавитом через замену букв другими буквами или символами).Второй период (с IX века на Ближнем Востоке (Ал-Кинди) и с XV века в Европе (Леон Баттиста Альберти) – до начала XX века) ознаменовался введением в обиход полиалфавитных шифров.
Третий период (с начала и до середины XX века) характеризуется внедрением электромеханических устройств в работу шифровальщиков. При этом продолжалось использование полиалфавитных шифров.
Четвёртый период (с середины до 70-х годов XX века) период перехода к математической криптографии. В работе Шеннона появляются строгие математические определения количества информации, передачи данных, энтропии, функций шифрования. Обязательным этапом создания шифра считается изучение его уязвимости к различным известным атакам – линейному и дифференциальному криптоанализу. Однако до 1975 года криптография оставалась «классической», или же, более корректно, криптографией с секретным ключом.
Современный период развития криптографии (с конца 1970-х годов по настоящее время) отличается зарождением и развитием нового направления – криптография с открытым ключом. Её появление знаменуется не только новыми техническими возможностями, но и сравнительно широким распространением криптографии для использования частными лицами (в предыдущие эпохи использование криптографии было исключительной прерогативой государства). Правовое регулирование использования криптографии частными лицами в разных странах сильно различается – от разрешения до полного запрета.
Современная криптография образует отдельное научное направление на стыке математики и информатики – работы в этой области публикуются в научных журналах, организуются регулярные конференции. Практическое применение криптографии стало неотъемлемой частью жизни современного общества – её используют в таких отраслях как электронная коммерция, электронный документооборот (включая цифровые подписи), телекоммуникации и других.
Введение
Кафедра "ИБ"
Слайд 3Атбаш
Даже в Библии можно найти примеры шифровок, хотя мало кто
это замечает. В книге пророка Иеремии (25,26) читаем: "...а царь
Сессаха выпьет после них." Такого царя или царства не было - неужели ошибка писца? Нет, просто порой священные иудейские тексты шифровались простой заменой. Вместо первой буквы алфавита писалась последняя, вместо второй - предпоследняя и так далее. Читая по нему слово СЕССАХ, на языке оригинала получаем слово ВАВИЛОН, и смысл библейского текста может быть принят даже не верящим слепо в истинность писания.Кафедра "ИБ"
Слайд 4Шифр моноалфавитной подстановки – это один из самых древних шифров
на Земле.
Прежде всего, выбирается нормативный алфавит, то есть набор
символов, которые будут использоваться при составлении сообщений, требующих зашифровки. Допустим, это будут прописные буквы русского алфавита (исключая буквы «Ё» и «Ъ») и пробел. Таким образом, нормативный алфавит будет состоять из 32 символов. Затем выбирается алфавит шифрования и устанавливается взаимно однозначное соответствие между символами нормативного алфавита и символами алфавита шифрования. Алфавит шифрования может состоять из произвольных символов, в том числе и из символов нормативного алфавита. При шифровании исходного сообщения, каждый символ открытого текста заменяется соответствующим ему символом алфавита шифрования.
Например, слово «ЗВЕЗДА» в зашифрованном виде будет выглядеть как «ИАТИЗН».
Шифр моноалфавитной подстановки
Кафедра "ИБ"
Слайд 5Простейшим примером моноалфавитных подстановок является шифр Цезаря. В этом шифре
каждый символ открытого текста заменяется третьим после него символом в
алфавите, замкнутом в кольцо, т.е. после пробела следует буква “А”. Таким образом, шифр Цезаря описывается так:Ei=( Mi + S ) mod N ,
где S - коэффициент сдвига, одинаковый для всех символов.
Цезарь использовал величину сдвига S=3, но, конечно, можно использовать любое целое S:
1 ≤ S ≤ (N-1).
Зашифруем, например, текст “ШИФР_ЦЕЗАРЯ”, используя коэффициент сдвига S=2.
Открытый текст: Ш И Ф Р _ Ц Е З А Р Я
Шифрованный текст: Ы К Ц Т Б Ш З Й В Т А
Шифр Цезаря
Кафедра "ИБ"
Слайд 6Какой-то хитрец из спартанцев обнаружил, что если полоску пергамента намотать
спиралью на палочку и написать на нем вдоль палочки текст
сообщения, то, после снятия полоски буквы на ней расположатся хаотично. Это то же самое, будто буквы писать не подряд, а через условленное число по кольцу до тех пор, пока весь текст не будет исчерпан. Сообщение ВЫСТУПАЙТЕ при окружности палочки в 3 буквы даст шифровку ВУТЫПЕСАТЙ. Текст ее не понятен, не так ли?“Cкитала”
Кафедра "ИБ"
Слайд 7Для прочтения шифровки нужно не только знать систему засекречивания, но
и обладать ключом в виде палочки, принятого диаметра. Зная тип
шифра, но не имея ключа, расшифровать сообщение сложно. Этот шифр называется “скитала” по названию стержня, на который наматывались свитки папируса, что указывает на его происхождение. Он был весьма популярен в Спарте и много раз совершенствовался в позднейшие времена. О его важном значении и большом распространении говорит свидетельство Плутарха, когда историк сообщает о жизни греческого полководца Алкивиада"Однако Лисандр обратил внимание на эти слова не раньше, чем получил из дома скиталу с приказанием отделаться от Алкивиада...“
"Сравнительные жизнеописания”
Плутарх
Кафедра "ИБ"
Слайд 8Квадрат Полибия
Древней Греции (П в. до н. э.) был известен
шифр, называемый "квадрат Полибия". Это устройство представляло собой квадрат 5x5,
столбцы и строки которого нумеровали цифрами от 1 до 5. В каждую клетку этого квадрата записывалась одна буква. (В греческом варианте одна клетка оставалась пустой, в латинском - в одну клетку помещали две буквы i и j.) В результате каждой букве отвечала пара чисел и шифрованное сообщение превращалось в последовательность пар чисел. Например:13 34 22 24 44 34 15 42 22 34 43 45 32
(Cogito ergo sum)
Это сообщение записано при использовании латинского варианта "квадрата Полибия ", в котором буквы расположены в алфавитном порядке.
Для русского алфавита обычно используют квадрат 5x6.
Код Полибия дошёл до наших дней и получил интересное название «тюремный шифр». Для его применения необходимо знать лишь естественный порядок расположения букв в алфавите. Число 3, например, передавалось путем трехкратного стука. При передаче буквы сперва отстукивалось число, соответствующее строке, в которой располагалась буква, а затем номер столбца. Например, буква «H» передавалась трехкратным стуком (третья строка) и затем однократным (первый столбец).
КВАДРАТ ПОЛИБИЯ
24 13 11 15 34 11 36
33 32 25 23 12 23 56
Кафедра "ИБ"
Слайд 9Существует еще один вариант шифрования при помощи «квадрата Полибия».
Для шифрования
на квадрате находили букву текста и вставляли в шифровку нижнюю
от нее в том же столбце. Если буква была в нижней строке, то брали верхнюю из того же столбца.Полибий
КВАДРАТ ПОЛИБИЯ
РИЖЛЦЖШ
ХФСПЗПЕ
Кафедра "ИБ"
Слайд 10Шифр четырех квадратов
Строят 4 квадрата размера 5х5 или 4х4 (в
зависимости от объема алфавита). В каждый из них случайным образом
записывают алфавит. Шифрование: Выбирая по 2 буквы сообщения, находим их соответственно в левом верхнем и правом нижнем квадрате. Для шифра используем 2 буквы, формирующих с выбранными вершины прямоугольника (слева направо)ХАКЕР
ДНЧЕЗН
Кафедра "ИБ"
Слайд 11Становление науки криптологии
Мы истину, похожую на ложь,
Должны хранить сомкнутыми устами,
Иначе
срам безвинно наживешь...
Данте. "Божественная комедия "После падения Римской империи от вторжения варваров в Европе пошли столетия упадка, которые историки образно назвали Темными веками. Все лучшие достижения цивилизации, а вместе с ними и криптология, были утрачены. По свидетельству святого Джерома "весь мир погрузился в руины". Лишь к концу средневековья применение криптографии начинает возрождаться. Например, книга "Экватор Планет", вышедшая в 1390 году и приписываемая Джефри Чосеру, содержит отдельные шифрованные главы.
Кафедра "ИБ"
Слайд 12Ручные шифры Средневековья
НЕЯСНОЕ СТАНОВИТСЯ ЕЩЕ БОЛЕЕ НЕПОНЯТНЫМ
НОНСБ НЯЕЕО
ЯОЕТЯ СВЕЛП НСТИЩ ЕОЫНА ТЕЕНМ
В ручных шифрах часто используются
таблицы, которые дают простые шифрующие процедуры перестановки букв в сообщении. Ключом в них служат размер таблицы, фраза, задающая перестановку или специальная особенность таблиц. Простая перестановка без ключа - один из самых простых методов шифрования, родственный шифру скитала. Кафедра "ИБ"
Слайд 13Перестановка колонок по ключу
до перестановки
после перестановки
СНЯНН БОЯЕТ ЕООЕЕ ПНЯВЛ
СЩОЫС ИЕТЕН МНТЕА
НЕЯСНОЕ СТАНОВИТСЯ ЕЩЕ БОЛЕЕ НЕПОНЯТНЫМ
Более практический метод
шифрования, называемый одиночной перестановкой по ключу. Он заключается в том, что колонки таблицы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы. Использовав в виде ключа слово ЛУНАТИК, получим такую таблицу. В верхней строке ее записан ключ, а номера под ключом определены по естественному порядку соответствующих букв ключа в алфавите. Если в ключе встретились бы одинаковые буквы, они бы нумеровались слева направо.
Кафедра "ИБ"
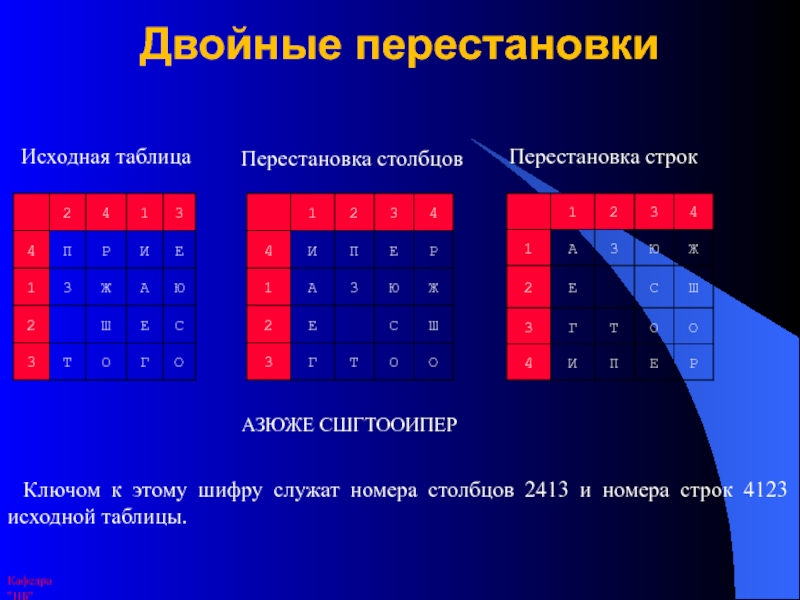
Слайд 14Двойные перестановки
Исходная таблица
Перестановка столбцов
Перестановка строк
АЗЮЖЕ СШГТООИПЕР
Ключом к
этому шифру служат номера столбцов 2413 и номера строк 4123
исходной таблицы.Кафедра "ИБ"
Слайд 15Магический квадрат
Альбрехт Дюрер
На известной гравюре Дюрера "Меланхолия" позади грустящего
ангела изображен магический квадрат, заполненный цифрами.
Дюрер составил первый в
европейском искусстве магический квадрат, 4х4. Сумма чисел в любой строке, столбце, диагонали, а также в каждой четверти (в том числе в центральном квадрате) и сумма угловых чисел равна 34. Два средних числа в нижнем ряду указывают дату создания картины (1514).Кафедра "ИБ"
Слайд 16Магический, или волшебный квадрат — это квадратная таблица n x
n, заполненная n2 числами таким образом, что сумма чисел в
каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Нормальным называется магический квадрат, заполненный целыми числами от 1 до n2. Магический квадрат называется ассоциативным или симметричным, если сумма любых двух чисел, расположенных симметрично относительно центра квадрата, равна n2 + 1.Сумма чисел в каждой строке, столбце и на диагоналях, называется магической константой, M. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой
Кафедра "ИБ"
Слайд 17Подобные квадраты широко применялись для вписывания шифруемого текста по приведенной
в них нумерации.
Если потом выписать содержимое таблицы по строкам, то
получалась шифровка перестановкой букв. Считалось, что созданные с их помощью шифровки охраняет не только ключ, но и магическая сила.ОИРТЗШЕЮ ЖАСЕГОП
Кафедра "ИБ"
Слайд 18Шифры замены цифр на буквы
Собственно, это коды, а не
шифры - вспомните обозначение месяцев на банках консервов, но код,
примененный единожды с неизвестной таблицей кодирования, схож по свойствам с шифром. Торговцы заранее договаривались использовать общее ключевое слово, буквы которого соответствовали бы цифрам. Например, для ключа РЕСПУБЛИКА цифра 0 означает букву Р, цифра 1 означает Е, 2 - С, 3-Н и так далее.Поэтому получив от корреспондента сообщение ПРИБЫВАЮ ЕЛРПАС, они его читали как ПРИБЫВАЮ 16/03/92. Простота и удобство этой системы шифрования позволили ей дожить до начала этого века без всяких изменений.
Кафедра "ИБ"
Слайд 19Шифр Гронсфельда
Состоит в модификации шифра Цезаря числовым ключом. Для
этого под сообщением пишут ключ. Если ключ короче сообщения, то
его повторяют циклически. Шифровку получают будто в шифре Цезаря, но отсчитывая необязательно только третью букву по алфавиту, а ту, которая сдвинута на соответствующую цифру ключа. Так, применяя в качестве ключа группу из трех начальных цифр числа "пи", а именно 314, получаем шифровку:Чтобы зашифровать первую букву сообщения С используя первую цифру ключа 3, отсчитывается третья по порядку от С в алфавите буква С-Т-У-Ф и получается буква шифровки Ф.
Кафедра "ИБ"
Слайд 20Шифрующие таблицы
Многие историки считают Иоганна Трисемуса, аббата из Германии,
вторым отцом современной криптологии. В 1508 году Трисемус написал "Полиграфию",
первую печатную работу по криптологии. В ней он первым систематически описал применение шифрующих таблиц, заполненных алфавитом в случайном порядке. Для получения такого шифра обычно использовались ключевое слово или фраза и таблица, которая для русского языка может иметь размер 5х6. Ключевое слово вписывалось в таблицу по строкам, а повторяющиеся буквы отбрасывались. Таблица дозаполнялась не вошедшими в нее буквами алфавита по порядку. Поскольку ключевое слово легко хранить в памяти, то такой подход упрощал процессы шифрования и дешифрования. Для ключа РЕСПУБЛИКА таблица будет иметь следующий вид:Как и в случае полибианского квадрата, при шифровании находят в этой таблице очередную букву открытого текста и записывают в шифртекст букву, расположенную ниже ее в том же столбце. Если буква текста оказывается в нижней строке таблицы, тогда для шифртекста берут самую верхнюю букву из того же столбца.
ВЫЛЕТАЕМПЯТОГО
НСДИЩМИЯЛБЩШОШ
Кафедра "ИБ"
Слайд 21Биграмные шифры
Трисемус первым заметил, что можно шифровать по две
буквы за раз. Такие шифры были названы биграммными. Наиболее известный
шифр биграммами Шифр Плейфера. Он применялся Великобританией в Первую мировую войну. Опишем его на примере той же самой таблицы. Открытый текст разбивался на пары букв (биграммы) и текст шифровки строился из него по следующим очень простым правилам.Если два символа биграммы совпадают, добавляем после первого символа «Х(Ь)», зашифровываем новую пару символов и продолжаем. В некоторых вариантах шифра Плейфера вместо «Х» используется «Q».
Если символы биграммы исходного текста встречаются в одной строке, то эти символы замещаются на символы, расположенные в ближайших столбцах справа от соответствующих символов. Если символ является последним в строке, то он заменяется на первый символ этой же строки.
Если символы биграммы исходного текста встречаются в одном столбце, то они преобразуются в символы того же столбца, находящиеся непосредственно под ними. Если символ является нижним в столбце, то он заменяется на первый символ этого же столбца.
Если символы биграммы исходного текста находятся в разных столбцах и разных строках, то они заменяются на символы, находящиеся в тех же строках, но соответствующие другим углам прямоугольника.
ПУСТЬ КОНСУЛЫ
БУДУТ БДИТЕЛЬНЫ
УБ РХ ЫИ ДО ПБ
КЩ РБ HP ШР
ЖЛ ФР ИЩ ЗЮ
Кафедра "ИБ"
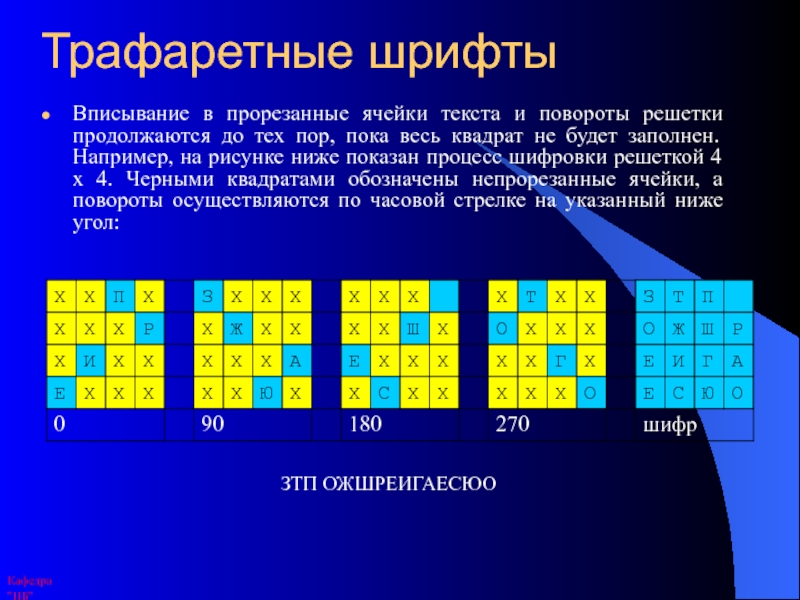
Слайд 22Трафаретные шрифты
Вписывание в прорезанные ячейки текста и повороты решетки продолжаются
до тех пор, пока весь квадрат не будет заполнен. Например,
на рисунке ниже показан процесс шифровки решеткой 4 х 4. Черными квадратами обозначены непрорезанные ячейки, а повороты осуществляются по часовой стрелке на указанный ниже угол:ЗТП ОЖШРЕИГАЕСЮО
Кафедра "ИБ"
Слайд 23Практическая часть
Зашифруйте свое ФИО с помощью:
атбаш;
шифра Цезаря (S – номер
по списку);
квадрата Полибия (2-мя способами);
шифра четырех квадратов (квадраты берутся из
примера);перестановкой колонок по ключу (таблица и ключ выбирается самостоятельно);
двойной перестановки (таблица и ключ выбирается самостоятельно);
магического квадрата (выбирается в зависимости от количества букв в ФИО);
шифра Гронсфельда (ключ – год рождения);
шифрующих таблиц (таблица 5х6, ключ выбирается самостоятельно);
Биграмных шифров (ключ выбирается самостоятельно).
Домашнее задание
Кафедра "ИБ"
Зашифруйте свое ФИО с помощью:
шифра Уитстона (таблица 5х6, ключ выбирается самостоятельно);
шифра ADFGX (ключ выбирается самостоятельно);
шифра замены с использованием небуквенных символов (символы придумать самостоятельно)
Содержание отчета
Титульный лист.
Теоретический вопрос. Пример использования криптографии в художественной литературе.
Ход (алгоритм выполнения) шифрования.