ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

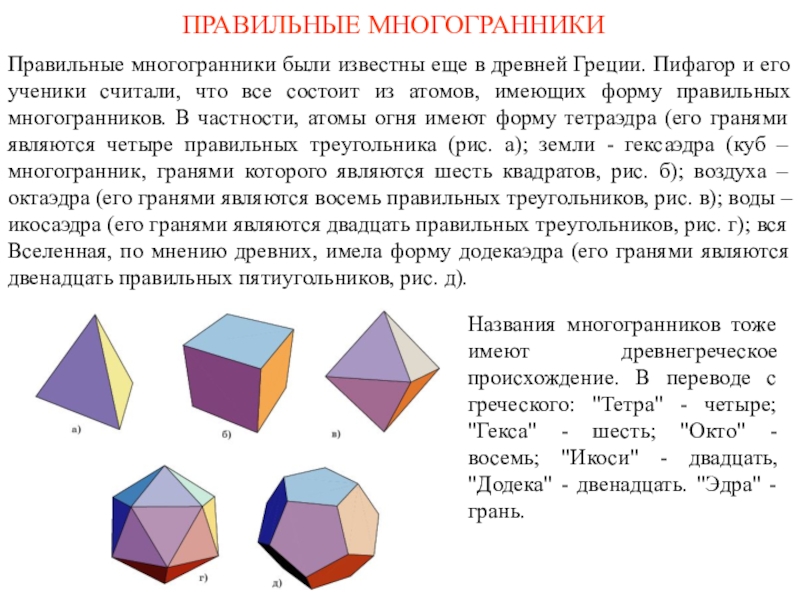
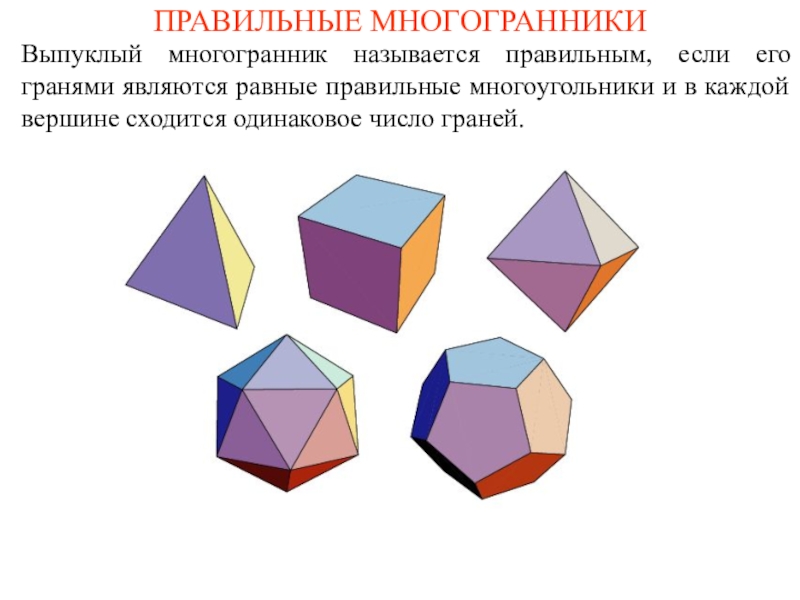
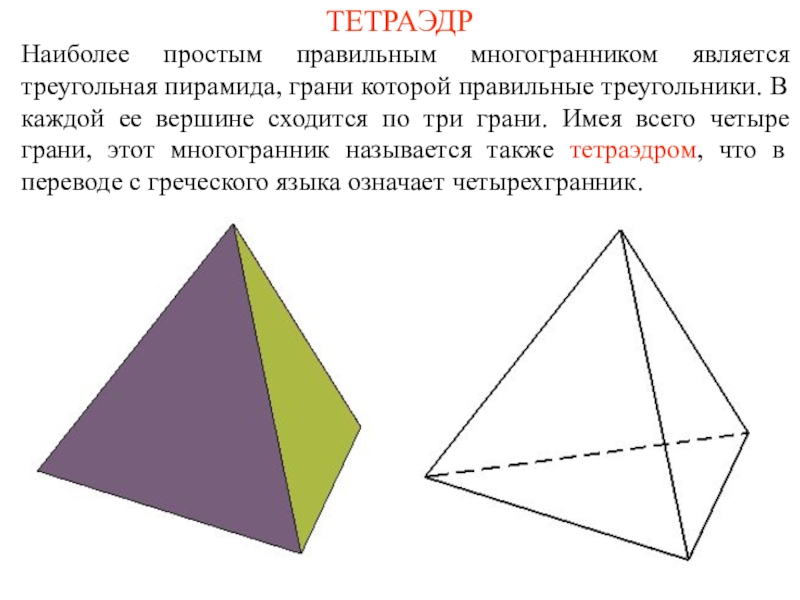
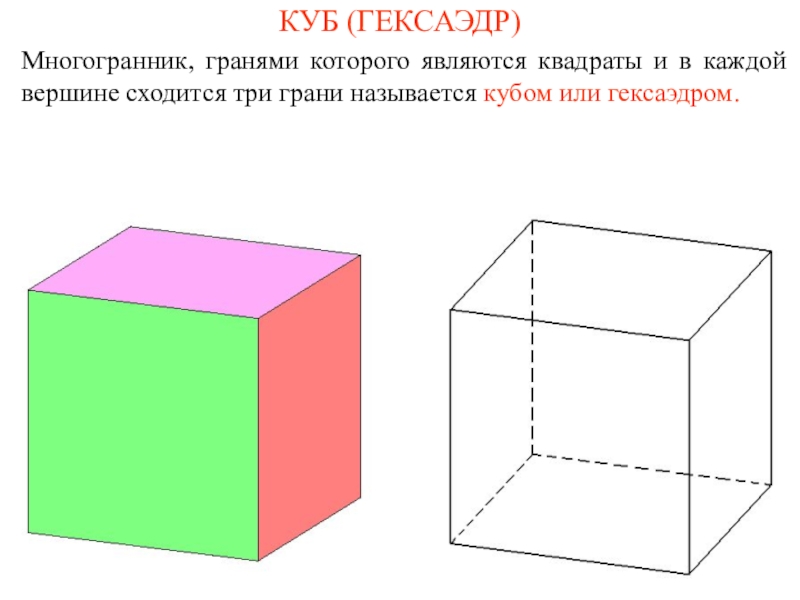
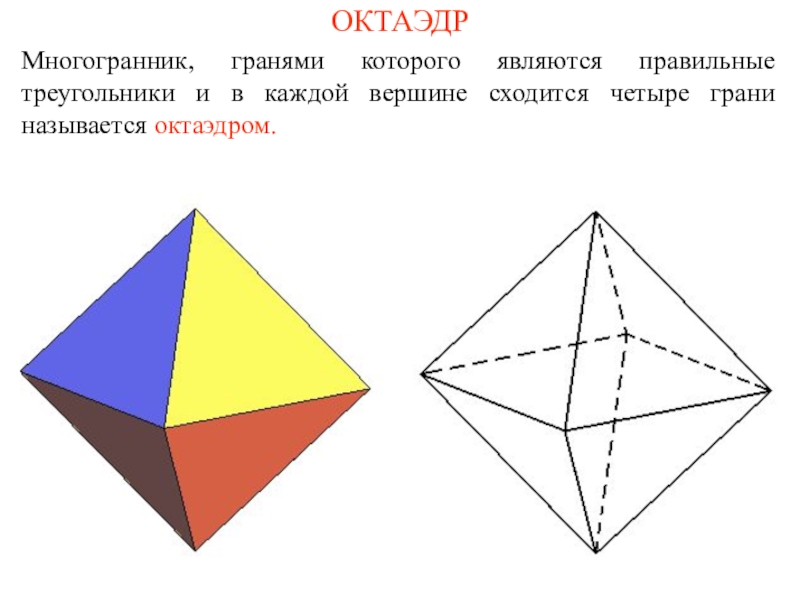
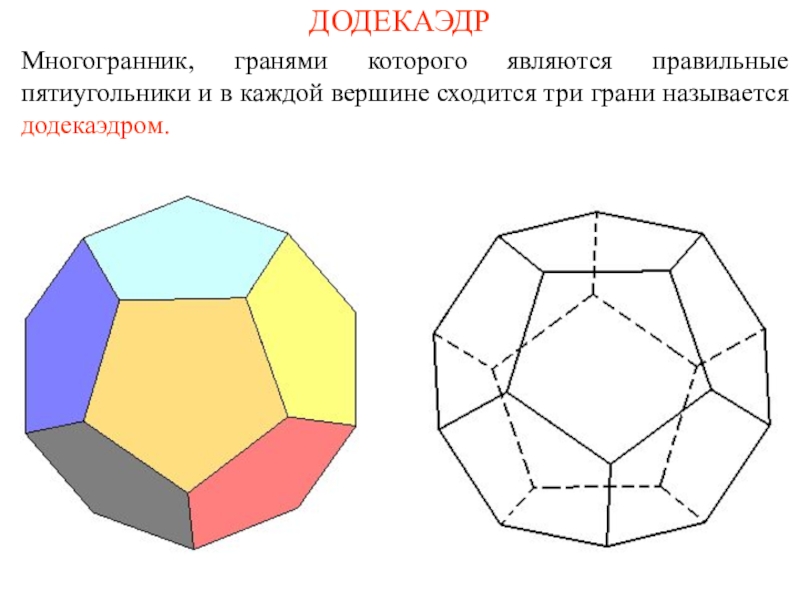
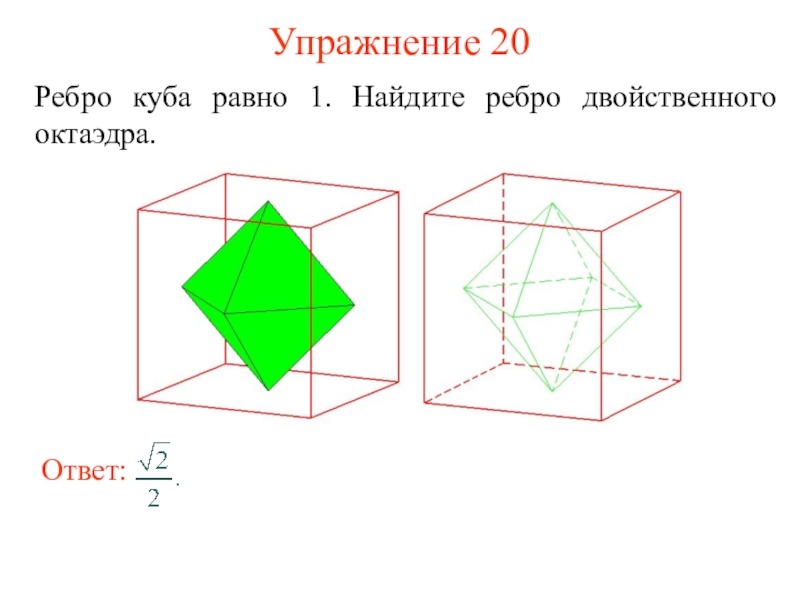
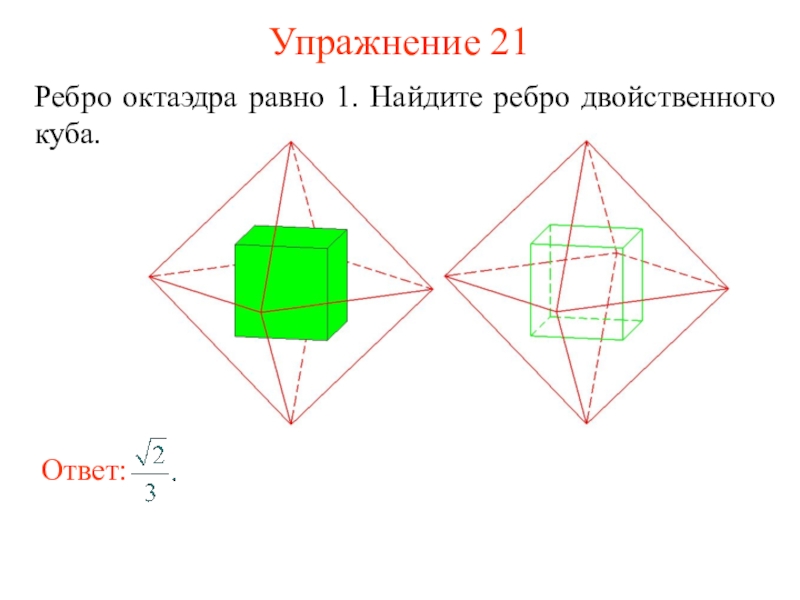
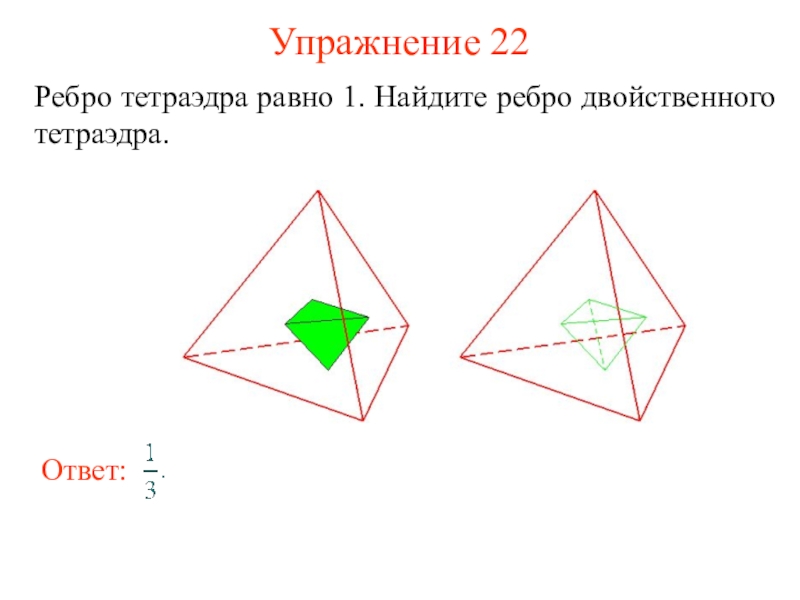
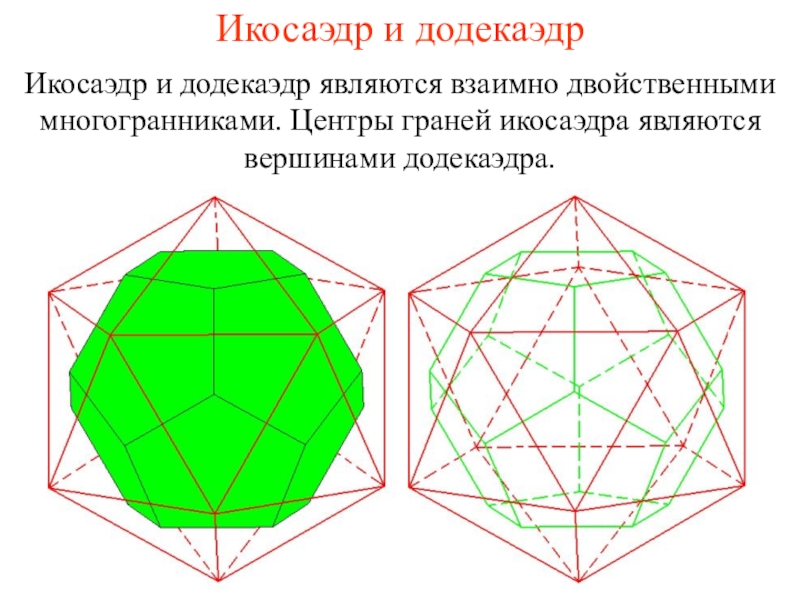
и его ученики считали, что все состоит из атомов, имеющих

форму правильных многогранников. В частности, атомы огня имеют форму тетраэдра (его гранями являются четыре правильных треугольника (рис. а); земли - гексаэдра (куб – многогранник, гранями которого являются шесть квадратов, рис. б); воздуха – октаэдра (его гранями являются восемь правильных треугольников, рис. в); воды – икосаэдра (его гранями являются двадцать правильных треугольников, рис. г); вся Вселенная, по мнению древних, имела форму додекаэдра (его гранями являются двенадцать правильных пятиугольников, рис. д).

Названия многогранников тоже имеют древнегреческое происхождение. В переводе с греческого: "Тетра" - четыре; "Гекса" - шесть; "Окто" - восемь; "Икоси" - двадцать, "Додека" - двенадцать. "Эдра" - грань.

первых своих работ "Тайна мироздания" в 1596 году, используя правильные

многогранники, вывел принцип, которому подчиняются формы и размеры орбит планет Солнечной системы. Геометрия Солнечной системы, по Кеплеру, заключалась в следующем: "Земля (имеется в виду орбита Земли) есть мера всех орбит. Вокруг нее опишем додекаэдр. Описанная вокруг додекаэдра сфера есть сфера Марса. Вокруг сферы Марса опишем тетраэдр. Описанная вокруг тетраэдра сфера есть сфера Юпитера. Вокруг сферы Юпитера опишем куб. Описанная вокруг куба сфера есть сфера Сатурна. В сферу Земли вложим икосаэдр. Вписанная в него сфера есть сфера Венеры. В сферу Венеры вложим октаэдр. Вписанная в него сфера есть сфера Меркурия". Такая модель Солнечной системы получила название "Космического кубка" Кеплера. Впоследствии, проведя более точные измерения, Кеплер пришел к выводу, что орбиты планет являются не окружностями, а эллипсами, при этом Солнце находится в одном из фокусов этих эллипсов. В этом состоит 1-ый закон Кеплера.

правильные многоугольники и в каждой вершине сходится одинаковое число граней.

треугольники. В каждой ее вершине сходится по три грани. Имея

всего четыре грани, этот многогранник называется также тетраэдром, что в переводе с греческого языка означает четырехгранник.

сходится три грани называется кубом или гексаэдром.

сходится четыре грани называется октаэдром.

икосаэдром.

сходится три грани называется додекаэдром.

Потому что в этом случае сумма плоских углов при вершинах

будет больше или равна 360о.

тетраэдров совмещением каких-нибудь их граней. Будет ли он правильным многогранником?

Ответ: Нет, в его вершинах сходится разное число граней.

додекаэдра.

тетраэдр;
б) куб;
в) октаэдр;
г) икосаэдр;
д) додекаэдр?
Ответ: а) В = 4, Р

= 6, Г = 4;

б) В = 8, Р = 12, Г = 6;

в) В = 6, Р = 12, Г = 8;

г) В = 12, Р = 30, Г = 20;

д) В = 20, Р = 30, Г = 12.

из них являются вершинами другого.
Куб и октаэдр являются взаимно двойственными

многогранниками. Центры граней куба являются вершинами октаэдра.

вершинами тетраэдра.

граней икосаэдра являются вершинами додекаэдра.

Какой многогранник ограничен этими плоскостями?

параллельно третьему ребру, выходящему из той же вершины куба, проведено

сечение, отсекающее от куба треугольную призму. Такие же сечения проведены через все возможные пары середин ребер, выходящих из вершин куба. Опишите многогранник, который останется от куба в результате этих отсечений. Сколько у него вершин, ребер и граней? Какую форму имеют грани? Нарисуйте этот многогранник.

вершины, проведены плоскости. Какой многогранник ограничен этими плоскостями?

двух тетраэдров. Какой многогранник является общей частью (пересечением) этих тетраэдров?
Ответ:

Октаэдр.

разные цвета. Какое минимальное число красок потребуется для правильной окраски

граней:

Ответ: 4.

а) тетраэдра;

б) куба;

в) октаэдра;

г) икосаэдра;

д) додекаэдра?

Ответ: 3.

Ответ: 2.

Ответ: 3.

Ответ: 4.