Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразование плоскости. Метод изучения симметрии в начальной школе
Содержание
- 1. Преобразование плоскости. Метод изучения симметрии в начальной школе
- 2. Введение Уже в раннем детстве человек
- 3. Изучение геометрических фигур, геометрических построений и геометрических
- 4. В настоящее время геометрический материал служит средством
- 5. Изучение Математика 1 класс 2 часть Истомина
- 6. Слайд 6
- 7. Слайд 7
- 8. Демидова, Козлова, Тонких (школа 2100)
- 9. Слайд 9
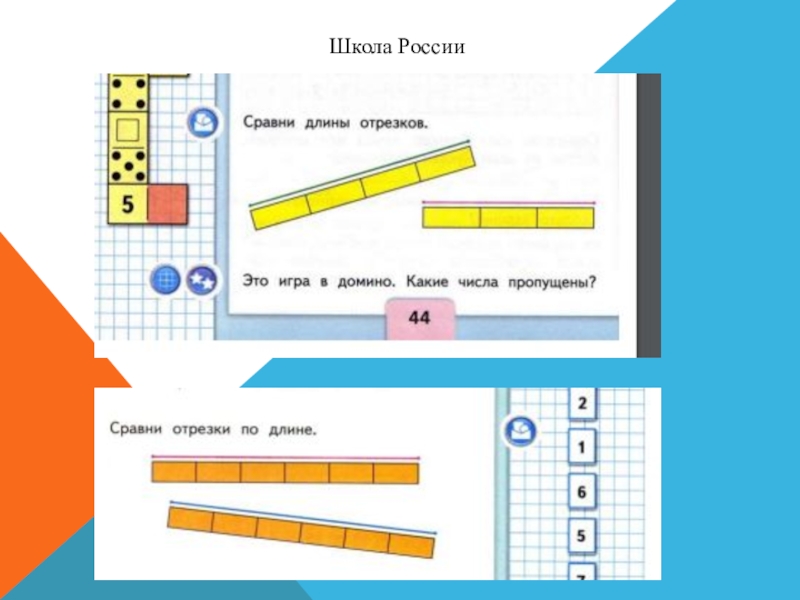
- 10. Школа России, Моро 1 класс 1часть
- 11. Выпускник получит возможность научиться распознавать, различать и называть
- 12. Для графического представления формы разработаны специальные правила изображений,
- 13. Источником плоскостных и линейных геометрических фигур являются
- 14. 1.2. Изучение линий, точек и плоскостных фигур.Линиягеометрическое
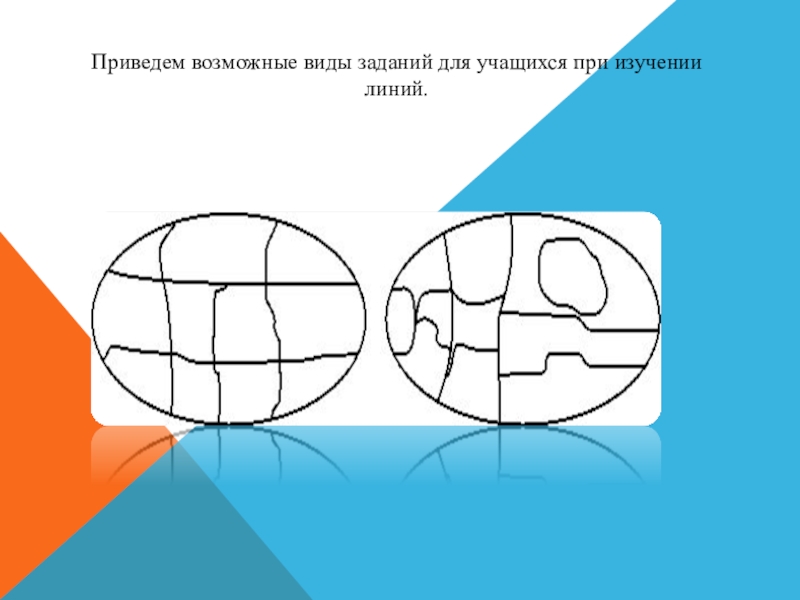
- 15. Приведем возможные виды заданий для учащихся при изучении линий.
- 16. Плоскостные фигурыПонятие «плоскостные фигуры» тесно связаны с
- 17. Обнаруживается, что в творениях рук человеческих наиболее
- 18. ТочкаТочке, как геометрической фигуре, обычно уделяется мало
- 19. 1.3. Простейшие геометрические построения в обучении младших
- 20. Школа России
- 21. прямого угла (на клетчатой бумаге и с
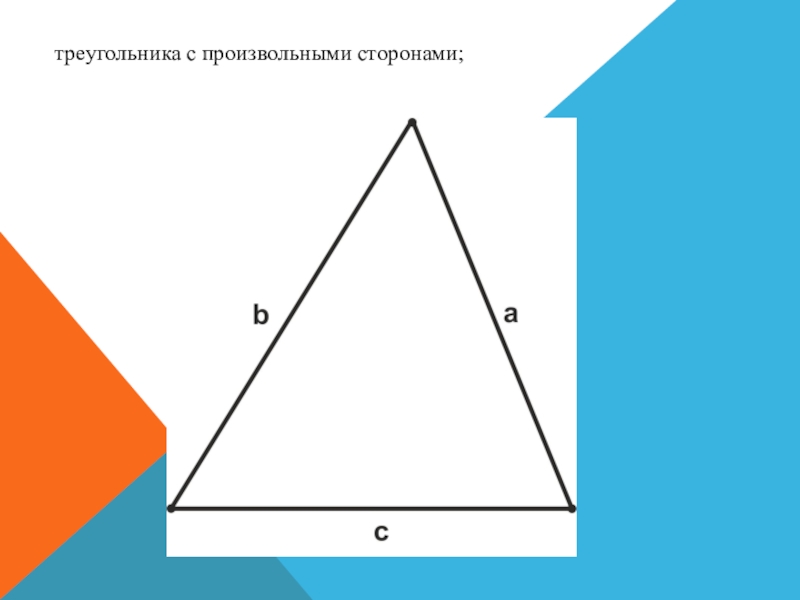
- 22. треугольника с произвольными сторонами;
- 23. четырехугольника с произвольными сторонами;
- 24. прямоугольника с заданными сторонами на клетчатой бумаге;
- 25. • окружности заданного радиуса.
- 26. Построение отрезка, равного имеющемуся, может быть выполнено
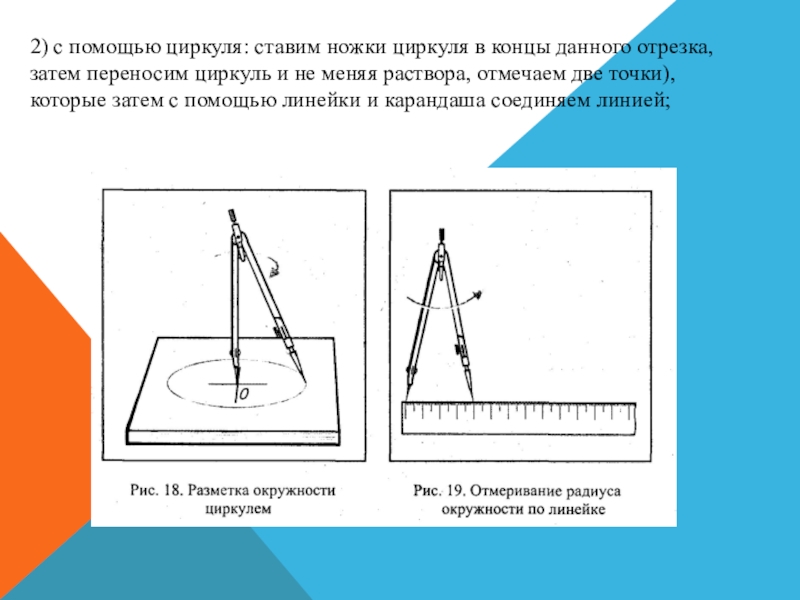
- 27. 2) с помощью циркуля: ставим ножки циркуля
- 28. Обучение геометрическим построениям происходит также при обучении
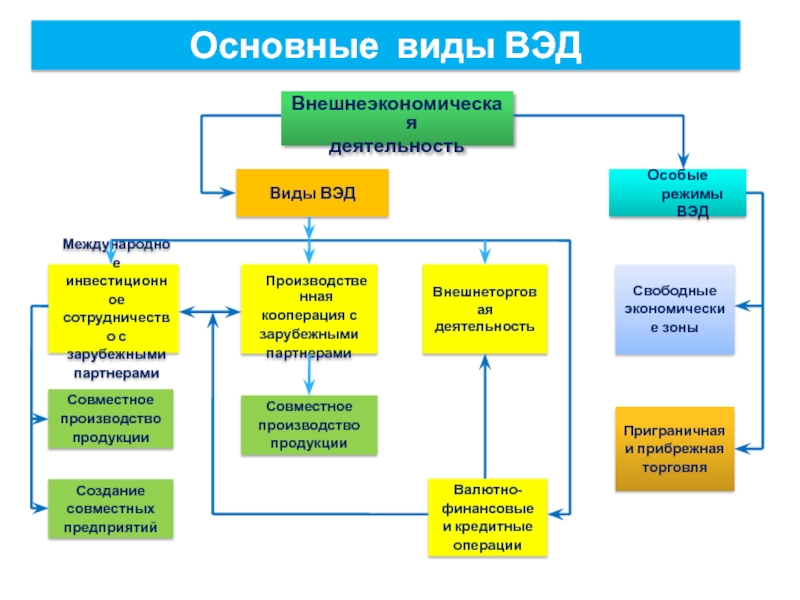
- 29. Геометрические преобразования в математическом образовании младших школьников.
- 30. На интуитивном уровне видимая осевая симметрия понятна
- 31. Как математические понятия параллельный перенос и поворот
- 32. Метод изучения симметрии в начальной школе. Тема
- 33. Формированию пространственного мышления способствует геометрический материал, оперирование
- 34. Анализируя учебники математики, выяснилось содержится ли в
- 35. Математика Школа России
- 36. Вывод Пространственное мышление – это мышление образами,
- 37. Спасибо за внимание!
- 38. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1«Преобразование плоскости. Метод изучения симметрии в начальной школе».
Выполнила студентка
гр.
ЗНОу-117:
Слайд 2Введение Уже в раннем детстве человек может быть очарован красотой бабочки,
снежинки, цветка, видеть совершенство великих сооружений, которые вызывают восхищение и
восторг. В школу ребёнок приходит уже с определёнными знаниями о геометрических фигурах, объектах, среди которых есть и симметричные. Включение в начальный курс математики темы «Симметрия», использование проектных технологий на уроках и во внеурочное время по формированию понятий о симметрии позволит развить у детей пространственное мышление, расширить знания о геометрических фигурах, подготовить детей к активному и осмысленному восприятию курса геометрии в средней школе. Детям свойственно в этом возрасте усваивать понятия с помощью наглядно-практических методов, игровых, проектных.Слайд 3Изучение геометрических фигур, геометрических построений и геометрических преобразований в начальной
школе 1.1. Общие подходы к изучению геометрических фигур в начальной школе. Современные
методические подходы, к изучению геометрического материала отражают изменения, которые произошли в начальной школе и обучении математике. В период реформ математического образования в начале 70-х годов XX в. геометрия не только вновь обрела полноправную прописку в начальной школе, но и заняла там значительное место. Большое внимание в геометрическом образовании младших школьников этого периода уделялось теории. Целью изучения геометрии в начальной школе стало — быть первой ступенью непрерывного школьного геометрического образования.Основная задача: обеспечить геометрическое развитие младших школьников на уровне умения «различать элементы фигур, устанавливать отношения между этими элементами и отдельными фигурами», овладение которым должно происходить «в процессе (и с помощью) наблюдений, измерения, вычерчивания, моделирования.
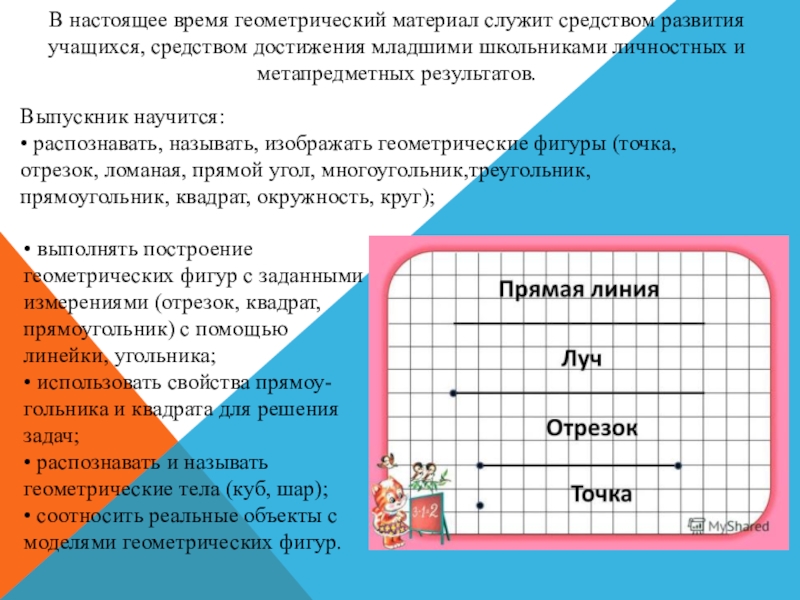
Слайд 4В настоящее время геометрический материал служит средством развития учащихся, средством
достижения младшими школьниками личностных и метапредметных результатов.
• выполнять построение геометрических
фигур с заданными измерениями (отрезок, квадрат, прямоугольник) с помощью линейки, угольника; • использовать свойства прямоу- гольника и квадрата для решения задач;
• распознавать и называть геометрические тела (куб, шар);
• соотносить реальные объекты с моделями геометрических фигур.
Выпускник научится:
• распознавать, называть, изображать геометрические фигуры (точка, отрезок, ломаная, прямой угол, многоугольник,треугольник, прямоугольник, квадрат, окружность, круг);
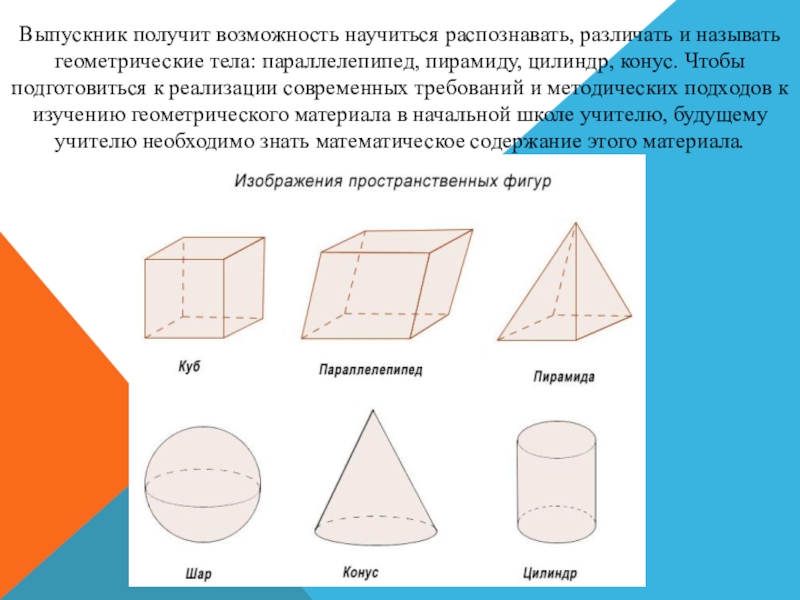
Слайд 11Выпускник получит возможность научиться распознавать, различать и называть геометрические тела: параллелепипед,
пирамиду, цилиндр, конус. Чтобы подготовиться к реализации современных требований и
методических подходов к изучению геометрического материала в начальной школе учителю, будущему учителю необходимо знать математическое содержание этого материала.Слайд 12Для графического представления формы разработаны специальные правила изображений, правила построения геометрических
фигур с использованием определенных наборов чертежных и измерительных инструментов.
Слайд 13Источником плоскостных и линейных геометрических фигур являются также формы линий
и ограничиваемых ими частей поверхностей. Изучаемые в начальной школе геометрические
фигуры могут «проявиться» в результате сравнения линий, узоров, контуров предметов, траекторий движений. Всем известно, как любят дети рисовать. Карандаши, ручки, фломастеры, мелки — любимые «инструменты» детей. Из-под их «пера» выходят линии самой разной формы. Комментируя рисунки, обучая рисованию, взрослые называют формы линий, их расположение относительно друг друга геометрическими терминами. Занятия изобразительной деятельностью оказывают значительное влияние на геометрическое развитие детей.Слайд 141.2. Изучение линий, точек и плоскостных фигур.
Линия
геометрическое понятие, точное и
в тоже время достаточно общее определение которого представляет значительные трудности
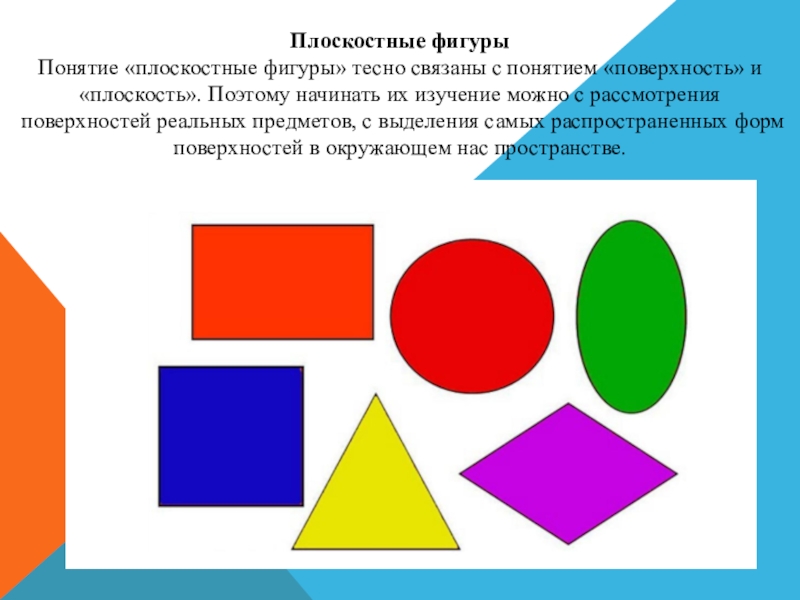
и осуществляется в различных разделах геометрии различно». Линию понимают как общую часть двух смежных областей поверхности, как границу поверхности, как траекторию или результат движения точки. Каждый из этих смыслов понятия линии должен быть представлен в обучении, а начать разговор о линиях можно с любого из них, например, с последнего.Слайд 16Плоскостные фигуры
Понятие «плоскостные фигуры» тесно связаны с понятием «поверхность» и
«плоскость». Поэтому начинать их изучение можно с рассмотрения поверхностей реальных
предметов, с выделения самых распространенных форм поверхностей в окружающем нас пространстве.Слайд 17Обнаруживается, что в творениях рук человеческих наиболее часто встречаются поверхности,
форма которых выражается прямоугольниками с неравными сторонами, квадратами, кругами, несколько
реже — треугольниками. Это формы поверхностей мебели, стен, крыш, книг, поверхности бытовой техники.Слайд 18Точка
Точке, как геометрической фигуре, обычно уделяется мало внимания. Ну что
ее рассматривать?! Ведь ухватиться не за что! Ни тебе длины,
ни ширины, ни высоты. Вообще — ничего! Но, можно ли без нее обойтись? Оказывается — нет. Без изобретения точки как обозначения отсутствия любых признаков, оказывается, не было бы и геометрии.Слайд 191.3. Простейшие геометрические построения в обучении младших школьников.
К простейшим задачам
на построение, обучение которым можно включать в задачи геометрического развития
учащихся начальной школы относят задачи на построение с помощью масштабной линейки, линейки и циркуля:• отрезка, равного по длине данному, большего (меньшего) на указанную длину данного;
Слайд 21прямого угла (на клетчатой бумаге и с помощью угольника на
нелинованной бумаге);
Школа 2100
Истомина Слайд 26Построение отрезка, равного имеющемуся, может быть выполнено тремя способами: 1)
прикладываем линейку к данному отрезку и напротив его концов на
линейке ставим метки, затем проводим в любом месте листа или от заданной точки линию от метки до метки;Слайд 272) с помощью циркуля: ставим ножки циркуля в концы данного
отрезка, затем переносим циркуль и не меняя раствора, отмечаем две
точки), которые затем с помощью линейки и карандаша соединяем линией;Слайд 28Обучение геометрическим построениям происходит также при обучении решению текстовых задач
с использованием геометрических моделей, при представлении информации на координатной прямой
или координатной плоскости. Основные функции обучения построениям в начальной школе — овладение учащимися умениями, достаточными для геометрических построений при изучении геометрического материала и построения геометрических моделей при решении текстовых задач и подготовка к решению задач на построение в основной школе.Слайд 29Геометрические преобразования в математическом образовании младших школьников.
Основные виды преобразований,
как известно, параллельный перенос и переносная симметрия, поворот и поворотная
симметрия, осевая и центральная симметрии. Самым важным и ярким преобразованием является симметрия. Идея симметрии является одной из самых продуктивных идей математики, способом пространственного упорядочивания материального мира и не только материального.Слайд 30На интуитивном уровне видимая осевая симметрия понятна даже первоклассникам. Самый
простой способ показа осевой симметрии — с помощью сгибания листа
бумаги. Сгибаем лист бумаги, от линии сгиба рисуем любую линию, чтобы в результате вместе с линией сгиба получилась замкнутая линия. Затем вырезаем нарисованное и разворачиваем лист. Мы получим две симметричные линии сгиба части листа.Слайд 31Как математические понятия параллельный перенос и поворот в начальной школе
не изучаются. Однако как практические действия соответствующие построения применяются прежде
всего на уроках изобразительной деятельности, в частности при рассмотрении декоративно-прикладного искусства, рисовании узора в полосе, круге.Слайд 32Метод изучения симметрии в начальной школе.
Тема «Симметрия» в начальном
курсе математики» рассмотрены особенности развития пространственного мышления у детей младшего
школьного возраста. Своевременно сформированное пространственное мышление является основой дальнейшего обучения ребёнка. У младших школьников преобладает наглядно-образное мышление, оно имеет сходство с пространственным.Перспективная начальная школа.
Слайд 33Формированию пространственного мышления способствует геометрический материал, оперирование графическими изображениями, а
также включение заданий о симметрии. Тема «Симметрия» интересовала учёных с
древних времён. Впервые понятие симметрия появилось у последователей Пифагора в первой научной школе в истории человечества. Это было в VI веке до нашей эры.Слайд 34Анализируя учебники математики, выяснилось содержится ли в учебниках материал по
теме «Симметрия», какие можно встретить задания, формирующие понятие «симметрия». Учебники
математики трёх учебно-методических комплектов: «Начальная школа XXI века» (автор В.Н. Рудницкая), «Школа России» (автор М.И. Моро), «Перспективная начальная школа» (автор А.Л. Чекин). Приходим к выводу, что в учебниках В.Н. Рудницкой и А.Л. Чекина предусмотрены при работе с детьми отдельные уроки, на которых происходит знакомство с понятием «симметрия». Авторы учебников подобрали задания практического характера, использовали наглядный материал. В учебниках М.И. Моро понятие «симметрия» не употребляется, но встречаются задания с симметричными фигурами с первого по четвёртый класс.Слайд 36Вывод
Пространственное мышление – это мышление образами, в которых отражены
пространственные характеристики объектов. В начальной школе перед учителем встает важнейшая
задача развития пространственного мышления, ведь именно на данном этапе получения образования происходит 10 активное формирование пространственных представлений. Важно вовремя их сформировать, от этого зависит успешность ребёнка в получении образования. Учитель должен воспользоваться творческими методами, наглядно-практическими, применять приемы построения геометрических фигур, деления их на части, моделирование, приём материализации геометрических образов.Пространственное мышление в начальной школе формируется на основе геометрического материала, немалое значение при этом имеет тема «Симметрия». Анализ научной литературы по данной теме позволил выяснить, что симметрию можно рассматривать как вид преобразований каких-либо объектов. Учёные, которые занимались изучением законов симметрии, формулировали научные теории, основанные на симметрии - Пифагор Самосский, Платон, Аристотель, Птолемей, Коперник, Галилео, Ньютон, Иэн Стюарт, Герман Вейль. Современные учёные продолжают изучать законы симметрии, открывая новые теоретические положения.