Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
презентация к кр
Содержание
- 1. презентация к кр
- 2. Пусть E={1,2,3,4,5,6,7}, A={2,3,6},B={1,4,6,7} і C={1,2,3,6}. Вычислить:(а)
- 3. type mnog=set of 1..7 ;var E,
- 4. P1:= E-A;P2:=E-(B+C);P3:=A* (E-C);P4:=(E-(A+C))+(E-(A+B));P5:=(E-A*(E-B))+B;P6:=(C-B)*(A-(E-C));procedure pechat (z:mnog); var i:integer;beginfor
- 5. 2) На множестве M = {1,2,3,4} задано
- 6. 3) На множестве Z задано отношение:(m,n)R1
- 7. Слайд 7
- 8. Основные свойства матриц бинарных отношений: Пусть R
- 9. антисимметричным, если в матрице отсутствуют единицы, симметричные
- 10. Слайд 10
- 11. Транзитивная
- 12. {A
- 13. procedure ymnog(a,b:typematrix; n,m:integer; var KP:typematrix);
- 14. Умножение двух матриц: for i:=1 to n
- 15. for i:=1 to n do for j:=1
- 16. for i:=1 to n do for j:=1
- 17. end; if ResTAS=True then writeln(g,'AS')else
- 18. for i:=1 to n do
- 19. for i:=1 to n do
- 20. if ResT2 and ResTS and ResTR then
- 21. Составить схему для доказательства формулы алгебры высказываний и заполнить таблицу истинности:
- 22. varP,Q,R,T,F:boolean;begin Write('P':6,'Q':6,'R':6,'T':6,'F':6); writeln;for P:=false to true do
- 23. Скачать презентанцию
Пусть E={1,2,3,4,5,6,7}, A={2,3,6},B={1,4,6,7} і C={1,2,3,6}. Вычислить:(а) ; (г) ();(б) ; (д) B;(в) A; (е) (C \ B) (A \ ).
Слайды и текст этой презентации
Слайд 2 Пусть E={1,2,3,4,5,6,7},
A={2,3,6},
B={1,4,6,7} і C={1,2,3,6}.
Вычислить:
(а) ; (г) ();
(б) ; (д)
B;
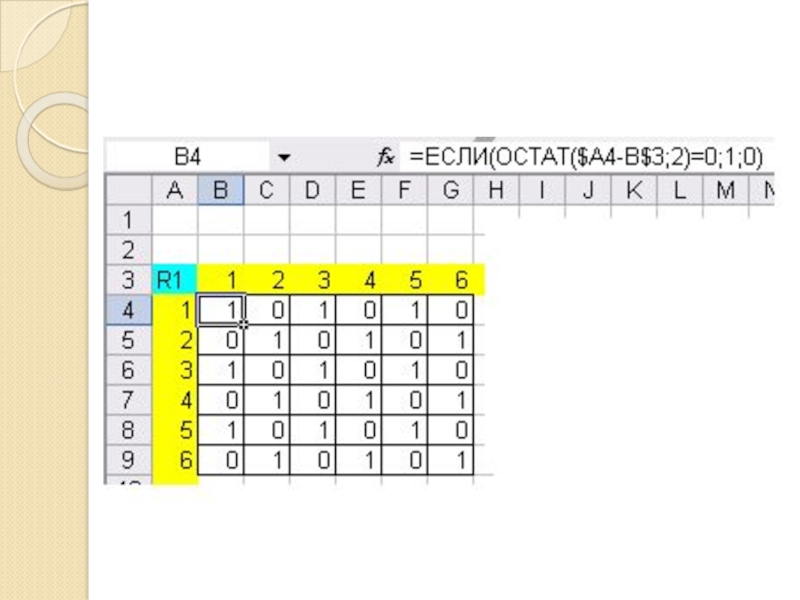
Слайд 3 type
mnog=set of 1..7 ;
var
E, A,C,B, P1,P2, P3,P4,P5,P6:
mnog; f:text;
begin
assign(f,'answer.txt');
rewrite(f);
A:=[2,3,6];
B:=[1,4,6,7];
C:=[1,2,3,6];E:=[1..7];
Слайд 4P1:= E-A;
P2:=E-(B+C);
P3:=A* (E-C);
P4:=(E-(A+C))+(E-(A+B));
P5:=(E-A*(E-B))+B;
P6:=(C-B)*(A-(E-C));
procedure pechat (z:mnog);
var i:integer;
begin
for i:=1 to 7
do
if i in z then write(f,i:4); writeln(f);
end;
Слайд 52) На множестве M = {1,2,3,4} задано отношение:
R1 = {(1,1),(1,3),(2,2),(2,4),(3,1),(3,3),(4,2),(4,4)};
R2
= {(1,1),(2,2),(2,3),(2,4),(3,1),(3,3),(4,1),(4,4)};
R3 = {(1,3),(1,4),(2,1),(1,2),(3,1),(3,3),(4,1)};
R4 = {(1,1),(1,2),(1,4),(2,2),(2,4),(3,3),(3,4),(4,2),
(4,3),(4,4)};
R5 = {(1,2),(1,3),(2,3),(2,4),(4,1),(4,3)}
R6 = {(1,1),(2,2),(2,3),(2,4),(3,1),(3,3),(4,1),(4,4)};
Слайд 63) На множестве Z задано отношение:
(m,n)R1 m-n парне число;
(m,n)R2
m+n парне число;
(m,n)R3 m-n 100;
(m,n)R4 m-n
непарне число;(m,n)R5 m+n непарне число;
(m,n)R6 m/n парне число;
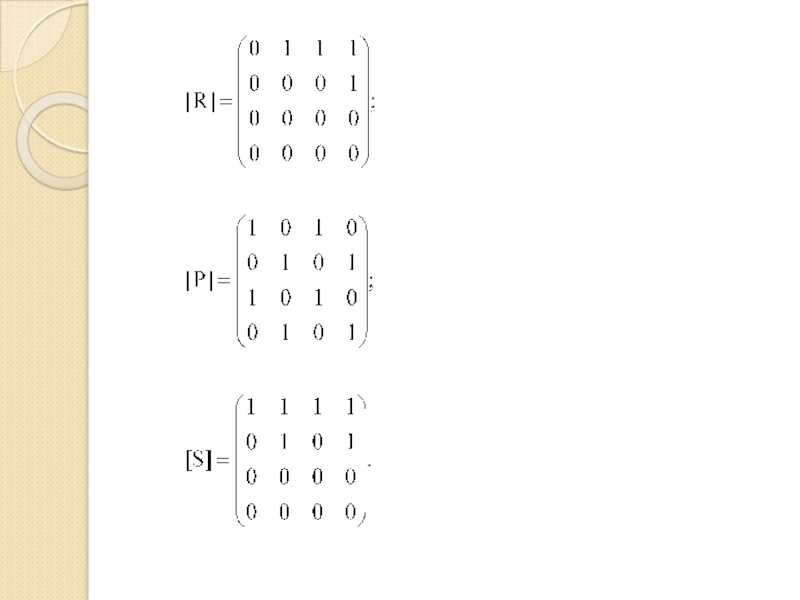
Слайд 8Основные свойства матриц бинарных отношений:
Пусть R – бинарное отношение на
A2. Тогда отношение R является:
рефлексивным, если на главной диагонали R
стоят единицы; антирефлексивным, если на главной диагонали R стоят нули;
симметричным, если [R]=[R]T (матрица симметрична относительно главной диагонали);
Слайд 9антисимметричным, если в матрице отсутствуют единицы, симметричные относительно главной диагонали;
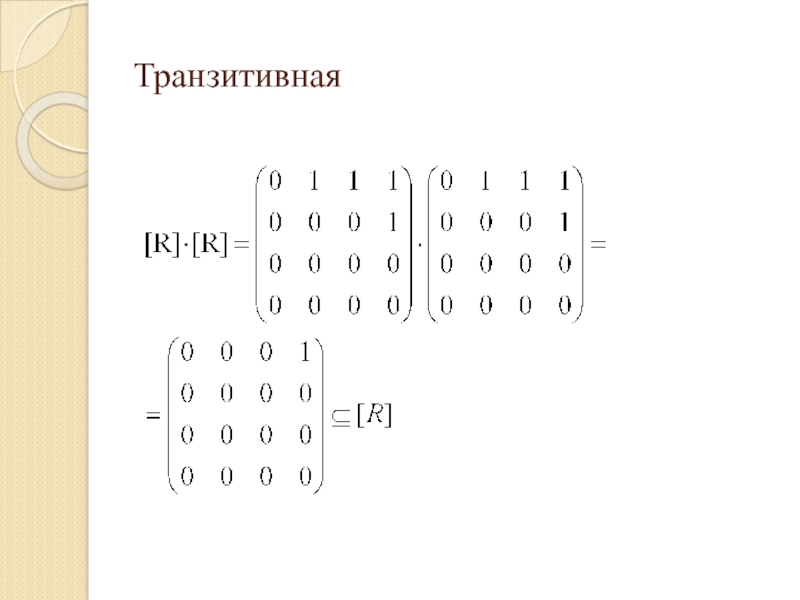
транзитивным,
если RR R. Матрица композиции [RR] = [R]
[R], где умножение матриц [R] и [R] выполняется обычным способом, но при этом, умножение элементов соответствует логическому «и» (00=10=01=0, 11=1), а сложение элементов – логическому «или» (0+0=0, 1+0=0+1=1+1=1).![антисимметричным, если в матрице отсутствуют единицы, симметричные относительно главной диагонали;транзитивным, если RR R. Матрица композиции [RR]](/img/thumbs/d6d4c29c219b725030bd4341211a3561-800x.jpg "презентация к кр антисимметричным, если в матрице отсутствуют единицы, симметричные относительно главной диагонали;транзитивным, если")
Слайд 12
{A размерность m*n}
{B размерность n*p}
{a,b – матрицы, которые будем умножать}{KP – результирующая матрица}
{n –количество столбцов первой матрицы}
{m – количество строк первой матрицы}
{n – количество строк второй матрицы}
{p - количество столбцов второй матрицы}
Процедура, осуществляющая умножение двух матриц:
Слайд 13 procedure ymnog(a,b:typematrix; n,m:integer; var KP:typematrix);
var
i,j,k:integer;
begin{ymnog}for i:=1 to m do
for j:=1 to p do
begin
C[i,j]:=0;
for k:=1 to n do
C[i,j]:=C[i,j]+a[i,k]*b[k,j];
end;
end;{ymnog}
Слайд 14Умножение двух матриц:
for i:=1 to n do
for j:=1 to
n dobegin
C[i,j]:=0;
for k:=1 to n do
C[i,j]:=C[i,j]+ar[i,k]*ar[k,j];
if c[i,j]>=1 then c[i,j]:=1;
end;
Слайд 15for i:=1 to n do
for j:=1 to n do
if (Ar[i,j]=Ar[j,i])
then
ResTS:=true
elsebegin
ResTS:=false;
break;
end;
if ResTS=True then writeln(g,'S')
else writeln(g,'NS')
![for i:=1 to n do for j:=1 to n do if (Ar[i,j]=Ar[j,i]) then](/img/thumbs/e606a1d7c6c64afe6853c41e26516c46-800x.jpg "презентация к кр for i:=1 to n do for j:=1 to n do")
Слайд 16for i:=1 to n do
for j:=1 to n do
if i j
then
beginif ((Ar[i,j]=0) and (Ar[j,i]=0))
then
ResTAS:=true
else
if (Ar[i,j]<>Ar[j,i])
then
ResTAS:=true
else
begin ResTAS:=false; break; end ;
Слайд 17end;
if ResTAS=True
then writeln(g,'AS')
else writeln(g,'NAS');
for i:=1 to
n do
if Ar[i,i]=1 then ResTR:=true
else beginResTR:=false;
break;
end;
if ResTR=True then writeln(g,'R')
else writeln(g,'NR');
![end; if ResTAS=True then writeln(g,'AS')else writeln(g,'NAS');for i:=1 to n do if Ar[i,i]=1 then](/img/thumbs/df8de13296f397181008cdcc910113aa-800x.jpg "презентация к кр end; if ResTAS=True then writeln(g,'AS')else writeln(g,'NAS');for i:=1 to n do")
Слайд 18
for i:=1 to n do
if Ar[i,i]=0 then
ResTAR:=true
else begin
ResTAR:=false;
break;end;
if ResTAR=True then writeln(g,'AR')
else writeln(g,'NAR');
![for i:=1 to n do if Ar[i,i]=0 then ResTAR:=true else begin](/img/thumbs/1f53fd00e5a5bc2b457ac046a7049330-800x.jpg "презентация к кр for i:=1 to n do if Ar[i,i]=0 then ResTAR:=true")
Слайд 19 for i:=1 to n do
for j:=1 to n do
beginif c[i,j]<= ar[i,j]
then
ResT2:=true
else begin
ResT2:=false; break; end;
end;
if ResT2=true then writeln(g,'T')
else writeln(g,'NT');
Слайд 20if ResT2 and ResTS and ResTR then writeln(g,'E');
if ResT2 and
ResTAS then writeln(g,'Order');
if ResT2 and ResTAS and ResTR then writeln(g,'Order
str');if ResT2 and ResTAS and ResTAR then writeln(g,'Order nestr');
Слайд 21
Составить схему для
доказательства формулы алгебры высказываний и заполнить таблицу истинности:
Слайд 22var
P,Q,R,T,F:boolean;
begin
Write('P':6,'Q':6,'R':6,'T':6,'F':6);
writeln;
for P:=false to true do
for Q:=false to
true do
for R:=false to true do
beginT:= P and (Q or R);
F:= (P and Q)or (P and R);
Write(P:6,Q:6,R:6,T:6,F:6);
Writeln;
end;
readln; end.
