Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прийняття рішень в умовах невизначеності
Содержание
- 1. Прийняття рішень в умовах невизначеності
- 2. Теорія Прийняття рішень © ЄА. Лавров, 2014-2019/14
- 3. Лекція 7. Прийняття рішень умовах невизначеності
- 4. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006/20 Проблема Прийняття рішень в умовах невизначеності
- 5. Прийняття рішень в умовах невизначеності Прийняття
- 6. Прийняття рішень в умовах невизначеності Прийняття
- 7. Прийняття рішень в умовах невизначеності. Відмінність
- 8. Теоретико-системные основы математического моделирования (с) Н.М. Светлов,
- 9. Критерії для прийняття рішень в умовах невизначеності.
- 10. 2.Критерії для прийняття рішень в умовах невизначеності.
- 11. 2.Критерії для прийняття рішень в умовах невизначеності.
- 12. 2.Критерії для прийняття рішень в умовах невизначеності.Критерий
- 13. 2.Критерії для прийняття рішень в умовах невизначеності.Критерий
- 14. 2.Критерії для прийняття рішень в умовах невизначеності.
- 15. 2.Критерії для прийняття рішень в умовах невизначеності.
- 16. 2.Критерії для прийняття рішень в умовах невизначеності.
- 17. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006/20 3. Приклади Прийняття рішень в умовах невизначеності
- 18. Теоретико-системные основы математического моделирования (с) Н.М. Светлов,
- 19. Теоретико-системные основы математического моделирования (с) Н.М. Светлов,
- 20. Теоретико-системные основы математического моделирования (с) Н.М. Светлов,
- 21. Теоретико-системные основы математического моделирования (с) Н.М. Светлов,
- 22. Теоретико-системные основы математического моделирования (с) Н.М. Светлов,
- 23. 4.Excel-технологія прийняття рішень в умовах невизначеності Теорія Прийняття рішень © ЄА. Лавров, 2014-2019/100
- 24. Теоретико-системные основы математического моделирования (с) Н.М. Светлов,
- 25. 5. Задачі прийняття рішень в умовах невизначеності
- 26. 5.Задачі прийняття рішень в умовах невизначеності Завдання
- 27. 5.Задачі прийняття рішень в умовах невизначеності
- 28. 5.Задачі прийняття рішень в умовах невизначеності Завдання
- 29. 5.Задачі прийняття рішень в умовах невизначеності Завдання
- 30. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Лекція 7. Прийняття рішень
умовах невизначеності
Зміст лекції:
Проблема Прийняття
рішень в умовах невизначеності
Критерії аналізу ситуації для прийняття
рішень в умовах невизначеності Приклади прийняття рішень в умовах невизначеності
Excel-технологія прийняття рішень в умовах невизначеності
Задачі прийняття рішень в умовах невизначеності
( для самост. опрацювання)
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/100
Слайд 4Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
Проблема Прийняття рішень
в умовах невизначеності
Слайд 5Прийняття рішень в умовах невизначеності
Прийняття рішень в умовах невизначеності,
як і в умовах ризику, вимагає визначення
альтернативних дій,
яким
відповідають платежі,які залежать від випадкових станів
природи.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 6Прийняття рішень в умовах невизначеності
Прийняття рішень в умовах невизначеності,
як і в умовах ризику, вимагає визначення альтернативних дій, яким
відповідають платежі, які залежать від випадкових станів природи.Матрицю платежів в задачі прийняття рішень з m можливими діями
та n станами природи можна представити таким чином.
Матриця платежів в задачі прийняття рішень
елемент sj - j-ий стан природи.
Елемент аi - i-e можливе рішення,
Плата (або прибуток ),
пов’язані з рішенням аi та станом sj, дорівнює v ( аi, sj).
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 7Прийняття рішень в умовах невизначеності.
Відмінність між прийняттям рішень в
умовах ризику та невизначеності
в умовах невизначеності
імовірнісний розподіл,
що
відповідає станам sj, j = 1, 2, ..., n,або невідомий, або не може бути визначений.
Цей недолік інформації зумовив розвиток спеціальних критеріїв
для аналізу ситуації,
пов'язаної з прийняттям рішень.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 8Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
2. Критерії аналізу
ситуації для прийняття рішень в умовах невизначеності
Слайд 9Критерії для прийняття рішень в умовах невизначеності.
Основні критерії
1.Крітерій
Лапласа 2.Мінімаксний критерій 3.Крітерій Севіджа 4.Крітерій Гурвіца
відрізняються за ступенем консерватизму,який проявляє ОПР, в умовах невизначеності.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 102.Критерії для прийняття рішень в умовах невизначеності. Критерій Лапласа
Спирається
на принцип недостатньої підстави, який свідчить, що, оскільки розподіл ймовірностей
станів P(si) невідомий, немає причин вважати їх різними.Отже, використовується оптимістичне припущення, що ймовірності всіх станів природи рівні між собою, тобто
P{s1} = P{s2} = ... = P{sn} = 1/n.
Якщо при цьому v(аi, sj) одержуваний прибуток, то найкращим рішенням є те, яке забезпечує
Якщо величина v(аi, sj)являє витрати ОПР, то оператор "max" замінюється на "min".
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 112.Критерії для прийняття рішень в умовах невизначеності. Мінімаксний (Максимінний )(критерій
Максимінний
(мінімаксний) критерій заснований на консервативному обережному поводженні ОПрі зводиться до
вибору найкращої альтернативи з найгірших.Якщо величина v(аi, sj) являє одержуваний прибуток, то відповідно до максиміного критерія
вибирається рішення, що забезпечує
Якщо величина v(аi, sj) являє втрати, використовується мінімаксний критерій, який визначається співвідношенням.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 122.Критерії для прийняття рішень в умовах невизначеності.Критерий Севіджа
Критерий Севіджа
прагне пом'якшити консерватизм мінімаксного (максимінного) критерію шляхом заміни матриці платежів
(виграшів або програшів) v(аi, sj) матрицею втрат r(аi, sj), , яка визначається наступним чином.Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 132.Критерії для прийняття рішень в умовах невизначеності.Критерий Севіджа
Теорія Прийняття
рішень
© ЄА. Лавров, 2014-2019
/14
© ЄА. Лавров, 2014-2019
Приклад технології “пом’якшення”.Щоб
показати, як критерій Севіджа "пом'якшує" мінімаксний (максимінний) критерій, розглянемо матрицю платежів v(аi, sj):Застосування мінімаксного критерію призводить до того, що рішення а2 з фіксованими втратами в 10 000 дол. є кращим.
Проте можна вибрати і а1 так як в цьому випадку існує можливість втратити лише 90 дол., якщо реалізується стан s2, при потенційному виграші 11000 дол. Подивимося, який результат вийде, якщо в мінімаксне критерії замість матриці платежів v(аi, sj) використовувати матрицю втрат r(аi, sj).
Як бачимо, мінімаксний критерій, застосований до матриці втрат, призводить до вибору рішення а1 як пріоритетного
Слайд 142.Критерії для прийняття рішень в умовах невизначеності.
Критерій Гурвіца
Охоплює ряд різних підходів
до прийняття рішень –від найбільш оптимістичного
до найбільш песимістичного(консервативного).
Нехай
0 <= а <= 1
Величини v(аi, sj) -доходи.
Тоді рішення, обране за критерієм Гурвіца:
Параметр а - показник оптимізму.
Якщо а = 0, критерій Гурвіца стає консервативним, бо його застосування еквівалентно застосуванню звичайного минимаксного критерію.
Якщо а = 1, критерій Гурвіца стає занадто оптимістичним, бо розраховує на найкращі з найкращих умов.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 152.Критерії для прийняття рішень в умовах невизначеності.
Критерій Гурвіца
Охоплює ряд різних підходів
до прийняття рішень –від найбільш оптимістичного
до найбільш песимістичного(консервативного).
Можна конкретизувати ступінь оптимізму (або песимізму)
належним вибором величини a з інтервалу [0,1].
При відсутності яскраво вираженої схильності до оптимізму або песимізму вибір а = 0,5 представляється
найбільш розумним.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 162.Критерії для прийняття рішень в умовах невизначеності.
Критерій Гурвіца
Якщо величини
v (аi, SJ) представляють втрати, то критерій приймає вигляд:
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 17Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
3. Приклади Прийняття
рішень в умовах невизначеності
Слайд 18Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
3. Приклади Прийняття
рішень в умовах невизначеності
Національна школа виживання підбирає місце для
будівництва літнього табору в центрі Аляски в цілях тренування людей на виживання в умовах дикої природи.Школа вважає, що число учасників збору може бути 200, 250, 300 або 350 осіб.
Вартість літнього табору буде мінімальною, оскільки він будується для задоволення тільки певних невеликих потреб.
Відхилення в бік зменшення або збільшення щодо ідеальних рівнів потреб тягнуть за собою додаткові витрати, зумовлені будівництвом надлишкових (невикористовуваних) потужностей або втратою можливості отримати прибуток у випадку, коли деякі потреби не задовольняються.
Нехай змінні a1 - a4 представляють можливі розміри табору (на 200, 250, 300 або 350 осіб),
а змінні S1 - S4 - відповідне число учасників збору.
Наступна таблиця містить матрицю вартостей (в тисячах доларів), що відноситься до описаної ситуації.
Слайд 19Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
3. Приклади Прийняття
рішень в умовах невизначеності
Національна школа виживання
Описана ситуація аналізується з
точки зору 4 розглянутих вище критеріїв1.Критерій Лапласа При заданих вірогідностях
P{s1} = 1/4, j = 1, 2, 3, 4,
очікувані значення витрат для різних можливих рішень обчислюються наступним чином.
M{a1} = (1/4)(5 + 10 + 18 + 25) = 14 500, М{a2} = (1/4)(8 + 7 + 12 + 23) = 12 500 - Оптимум, М{a3} = (1/4)(21 + 18 + 12 + 21) = 18 000, М{a4} = (1/4)(30 + 22 + 19 + 15) = 21 500.
Min
Слайд 20Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
3. Приклади Прийняття
рішень в умовах невизначеності
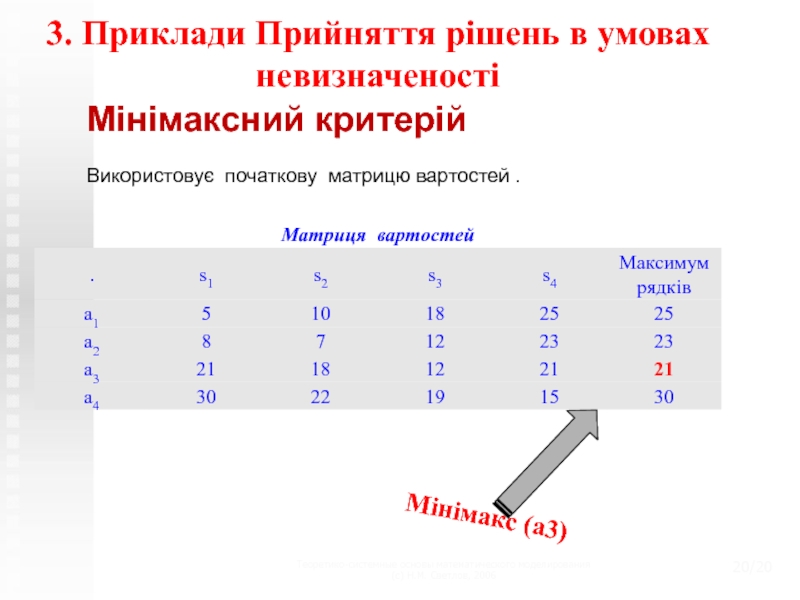
Мінімаксний критерій
Використовує початкову матрицю вартостей .
Мінімакс (a3)
Слайд 21Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
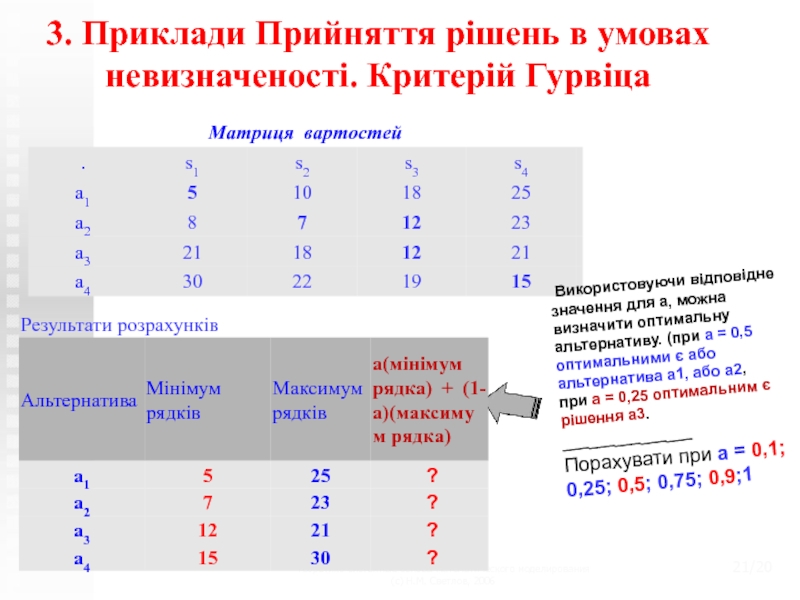
3. Приклади Прийняття
рішень в умовах невизначеності. Критерій Гурвіца
Використовуючи відповідне значення для
а, можна визначити оптимальну альтернативу. (при а = 0,5 оптимальними є або альтернатива а1, або a2, при а = 0,25 оптимальним є рішення a3.
_______________
Порахувати при а = 0,1; 0,25; 0,5; 0,75; 0,9;1
Слайд 22Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
3. Приклади Прийняття
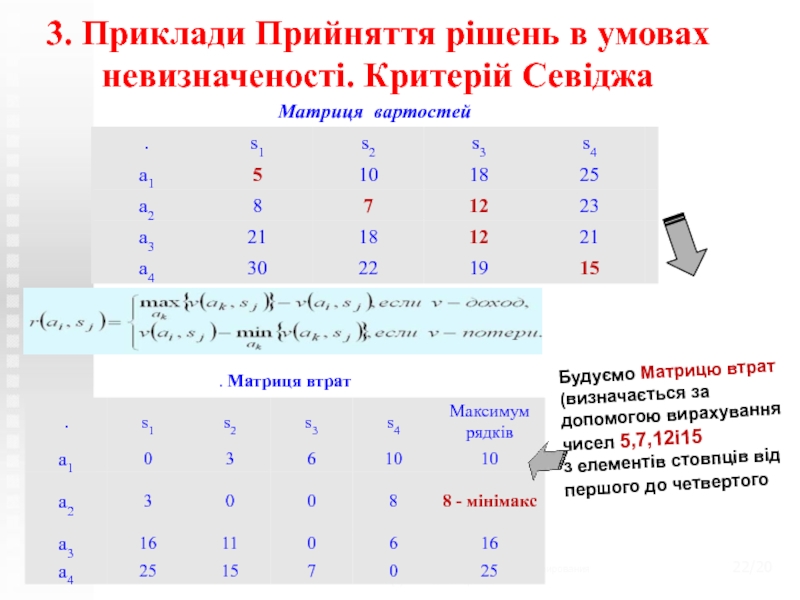
рішень в умовах невизначеності. Критерій Севіджа
Будуємо Матрицю втрат (визначається за
допомогою вирахування чисел 5,7,12і15з елементів стовпців від першого до четвертого
Слайд 23
4.Excel-технологія прийняття рішень в умовах невизначеності
Теорія Прийняття рішень
©
ЄА. Лавров, 2014-2019
/100
Слайд 24Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
4. Excel-технологія прийняття
рішень в умовах невизначеності
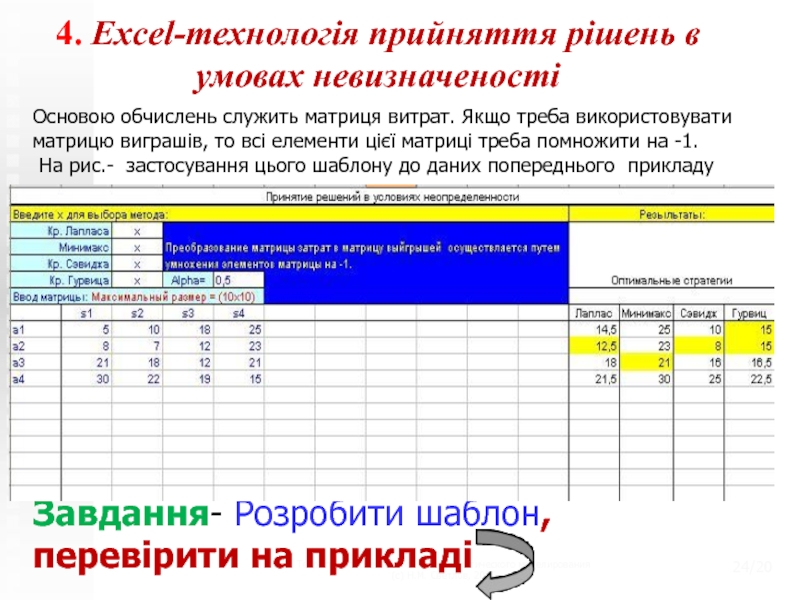
Основою обчислень служить матриця витрат. Якщо
треба використовувати матрицю виграшів, то всі елементи цієї матриці треба помножити на -1.На рис.- застосування цього шаблону до даних попереднього прикладу
Завдання- Розробити шаблон, перевірити на прикладі
Слайд 25
5. Задачі прийняття рішень в умовах невизначеності
( для самост.
опрацювання)
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/100
Слайд 265.Задачі прийняття рішень в умовах невизначеності
Завдання 1. Андрій - старанний
студент, який зазвичай отримує хороші позначки завдяки, зокрема, того, що
має можливість повторити матеріал в ніч перед іспитом. Перед завтрашнім іспитом Андрій зіткнувся з невеликою проблемою. Його однокурсники організували на всю ніч вечірку, в якій він хоче брати участь. Андрій має три альтернативи: a1 - брати участь у вечірці всю ніч, a2 - половину ночі брати участь у вечірці, а половину - вчитися, a3 - вчитися всю ніч. Професор, який приймає завтрашній іспит, непередбачуваний, і іспит може бути легким (S1), середнім (s2) або важким (S3). Залежно від складності іспиту і часу, витраченого Андрієм на повторення, можна чекати наступні екзаменаційні бали.Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Запропонуйте Андрію, який вибір він повинен зробити (грунтуючись на кожному з чотирьох критеріїв прийняття рішень в умовах невизначеності).
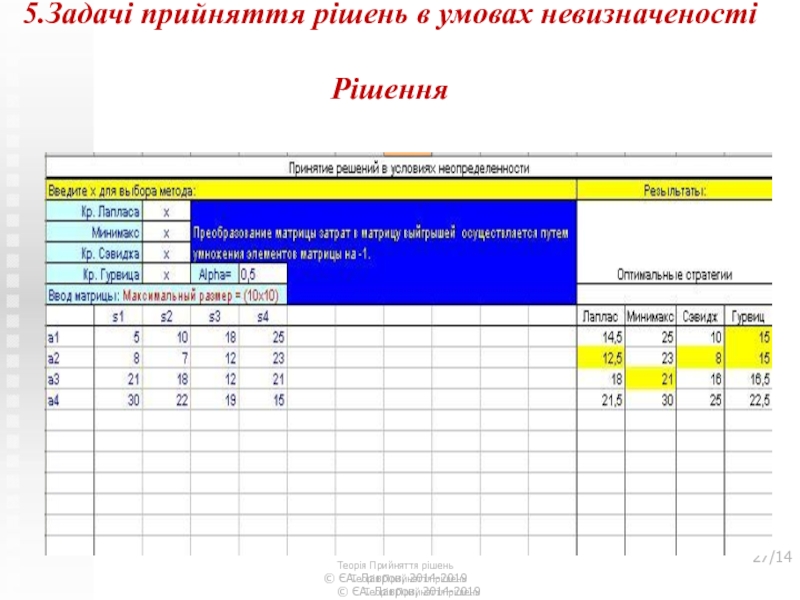
Слайд 275.Задачі прийняття рішень в умовах невизначеності
Рішення
Теорія Прийняття рішень
© ЄА.
Лавров, 2014-2019
/14
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 285.Задачі прийняття рішень в умовах невизначеності
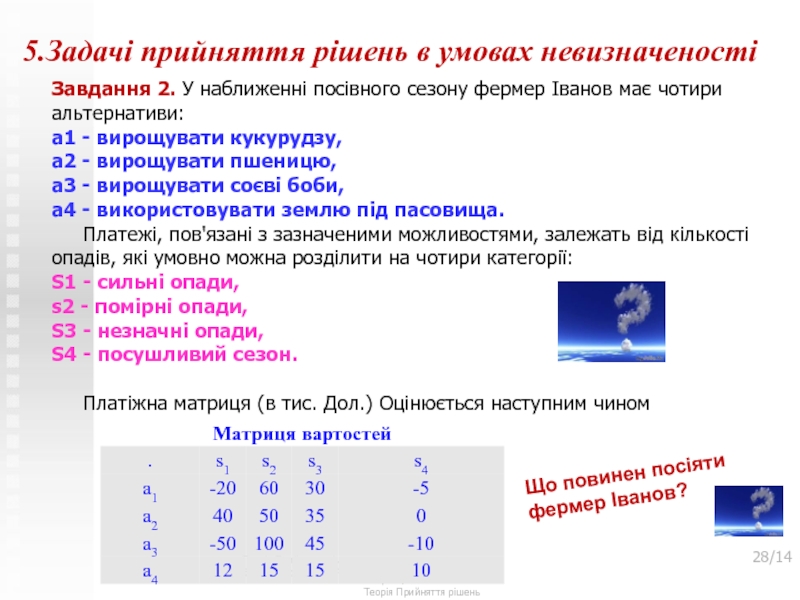
Завдання 2. У наближенні посівного
сезону фермер Іванов має чотири альтернативи: a1 - вирощувати кукурудзу, a2 -
вирощувати пшеницю, a3 - вирощувати соєві боби, a4 - використовувати землю під пасовища. Платежі, пов'язані з зазначеними можливостями, залежать від кількості опадів, які умовно можна розділити на чотири категорії: S1 - сильні опади, s2 - помірні опади, S3 - незначні опади, S4 - посушливий сезон. Платіжна матриця (в тис. Дол.) Оцінюється наступним чиномТеорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Що повинен посіяти фермер Іванов?
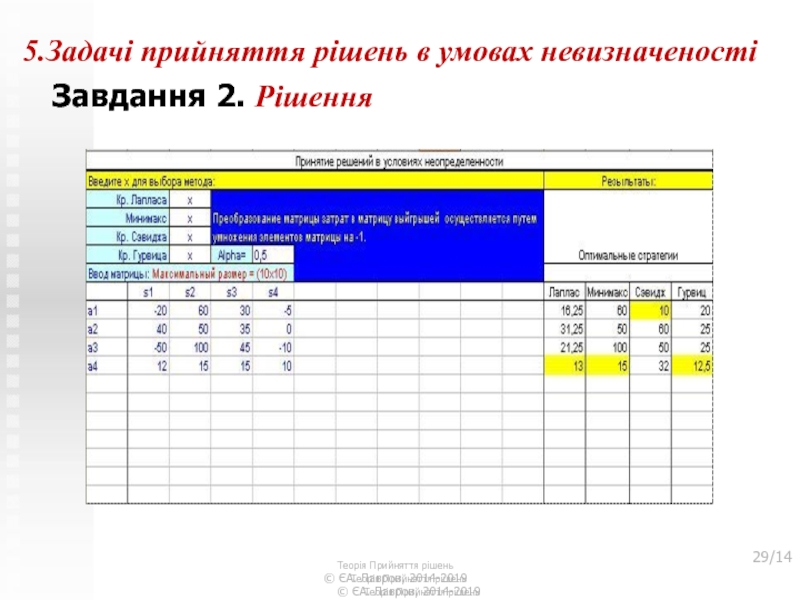
Слайд 295.Задачі прийняття рішень в умовах невизначеності
Завдання 2. Рішення
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Теорія
Прийняття рішень © ЄА. Лавров, 2014-2019
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019