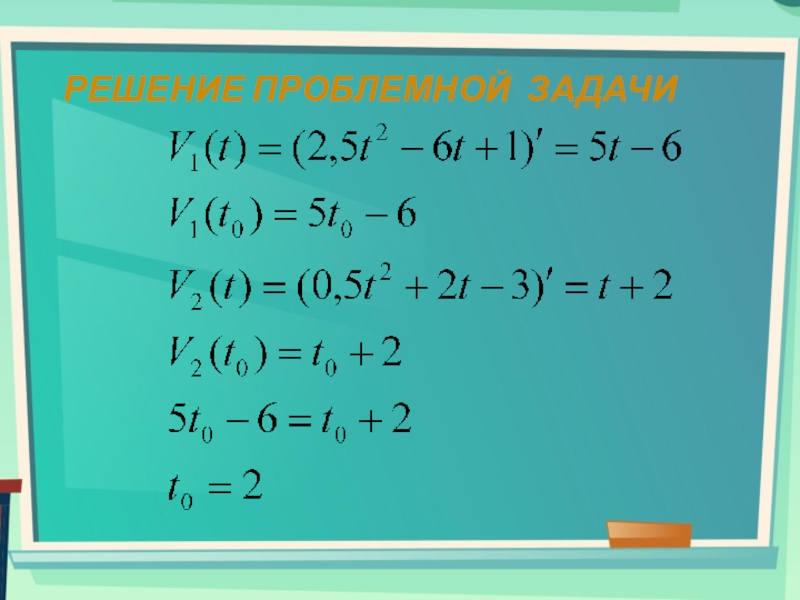Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приращение функции и аргумента. Производные простейших функций
Содержание
- 1. Приращение функции и аргумента. Производные простейших функций
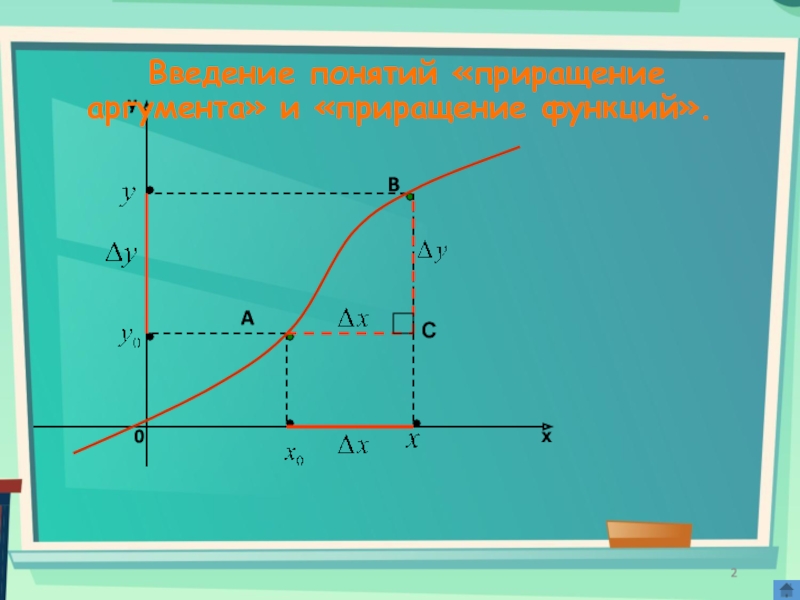
- 2. AB Введение понятий «приращение аргумента» и «приращение функций».С
- 3. Определение 2: Разность y - y0 называют приращением функции.
- 4. Предел отношения приращения функции
- 5. Операция вычисления производной называется дифференци-рованием.Функция называется дифференци-руемой
- 6. Алгоритм нахождения производной для функции y=f(x)1. Даем
- 7. Пример вычисления производнойРешение
- 8. Касательная и секущая к графику функции. Геометрический и физический смысл производной.
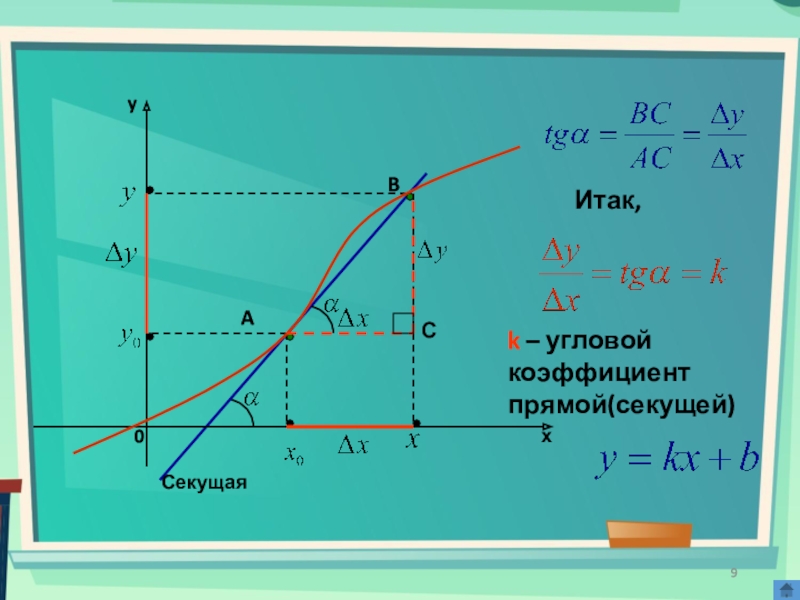
- 9. AB СекущаяСИтак,k – угловой коэффициент прямой(секущей)
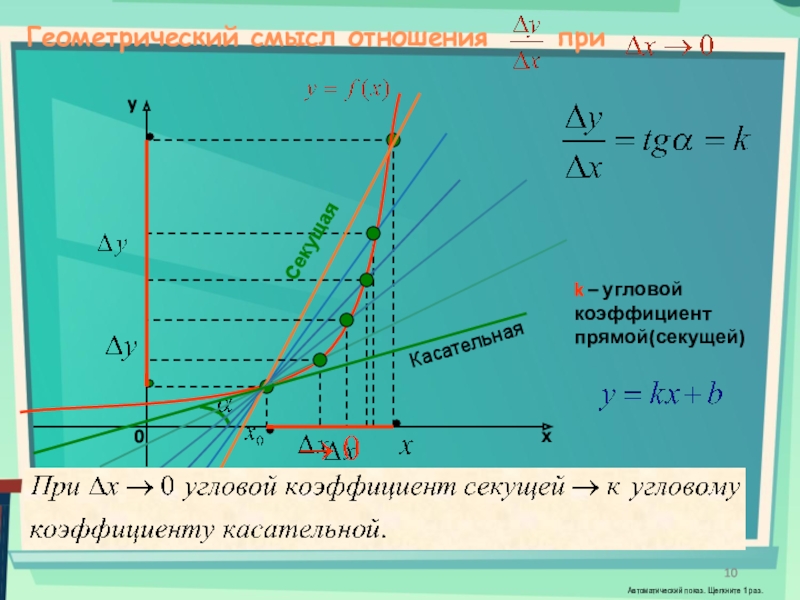
- 10. Геометрический смысл отношения при
- 11. Слайд 11
- 12. Алгоритм составления уравнения касательной к графику функции
- 13. Рассмотрим возможные типы задач на касательную
- 14. Ключевая задача 1. Составьте уравнение касательной
- 15. Задача 2 . Составьте уравнение касательной к
- 16. Физический смысл производной функции в данной точкеЕсли
- 17. Точка движется прямолинейно по закону
- 18. Найдите скорость и ускорение для точки, движущейся
- 19. Проблемная задачаДве материальные точки движутся прямолинейно по законам В какой момент времени скорости их равны, т.е.
- 20. Решение проблемной задачи
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4Предел отношения приращения функции к приращению аргумента
при условии , что
- называется производной данной функции и имеет вид:Определение.
Слайд 5Операция вычисления производной называется дифференци-рованием.
Функция называется дифференци-руемой в данной точке,
если в этой точке существует её производная.
Слайд 6Алгоритм нахождения производной для функции y=f(x)
1. Даем аргументу Х приращение
: Х +
2. Найдем наращенное значение функции, т.е. :
у (х + ).3. Вычисляем приращение функции:
4. Составляем отношение приращения функции к приращению аргумента:
5. Находим предел отношения при :
.
Слайд 10Геометрический смысл отношения при
k – угловой коэффициент прямой(секущей)
Секущая стремится занять
положение касательной. То есть, касательная есть предельное положение секущей.Секущая
Автоматический показ. Щелкните 1 раз.
Слайд 11
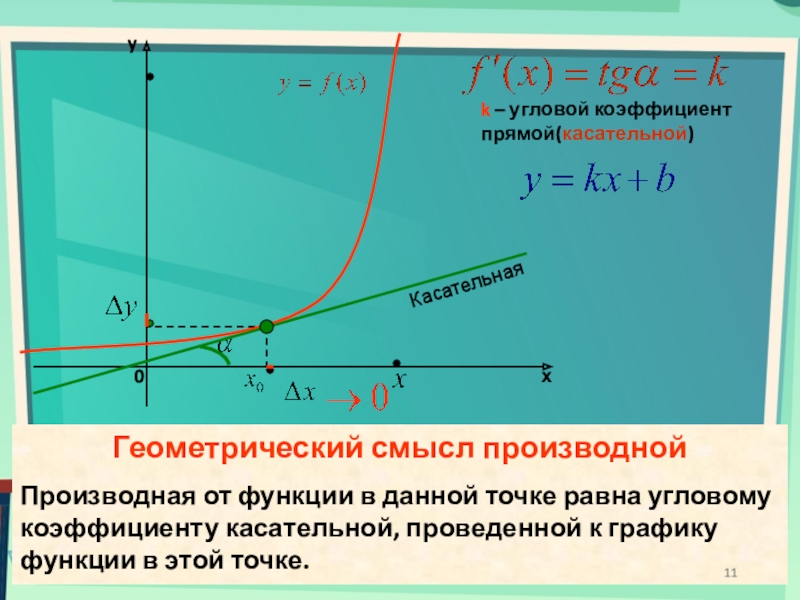
k –
угловой коэффициент прямой(касательной)
Касательная
Геометрический смысл производной
Производная от функции в данной точке
равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.Слайд 12Алгоритм составления уравнения касательной к графику функции y = f(x)
1. Обозначить буквой a абсциссу точки касания.
2. Найти f(a).
3. Найти f '(x) и f '(a).
4. Подставить
найденные числа a, f(a), f '(a) в общее уравнение касательной y = f(a) + f '(a)(x – a).
Слайд 14 Ключевая задача 1. Составьте уравнение касательной к графику функции
у=х2–2х–3 в точке с абсциссой х0=2.
Решение. 1. Обозначим абсциссу точки
касания а, тогда а=2.2. Найдем f(a): f(a)=22–2·2–3, f(a)=-3.
3. Найдем f’ (x) и f’(a): f’(x)=2x–2, f’(a)=2.
4. Подставим найденные числа а, f(a), в общее уравнение касательной у=f(a)+f’(a)(x–a): у=-3+2(х–2),
у=-3+2х–4, у=2х–7 – уравнение касательной.
Ответ: у = 2х –7.
Слайд 15Задача 2 . Составьте уравнение касательной к графику функции
в точке M(3; – 2).
Решение. Точка M(3; – 2) является
точкой касания, так как1. a = 3 – абсцисса точки касания.
2. f(3) = – 2.
3. f '(x) = x2 – 4, f '(3) = 5.
4. y = – 2 + 5(x – 3),
y = 5x – 17 – уравнение касательной.
Слайд 16Физический смысл производной функции в данной точке
Если материальная точка движется
прямолинейно и ее координата изменяется по закону x(t), то скорость
ее движения v(t) в момент времени t равна производной т.е. производная от координаты по времени есть скоростьПроизводная от скорости по времени есть ускорение:
Ускорение движения есть скорость изменения скорости, поэтому ускорение движения в момент времени t равно производной
Слайд 17
Точка движется прямолинейно по закону
Вычислите скорость
движения точки:
а) в момент времени t;
б) в момент времени t=2с.
Решение.
а)
б)
Задача 1