Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
профессор Ельцов Анатолий Викторович Ламинарное и турбулентное течения
Содержание
- 1. профессор Ельцов Анатолий Викторович Ламинарное и турбулентное течения
- 2. Течения жидкостейЕсли течение плавное и слои жидкости
- 3. Течения жидкостей
- 4. Поток жидкости и уравнение неразрывностиВыберем достаточно малый
- 5. Скорость движения кровиИз сердца кровь поступает в
- 6. Уравнение Бернулли
- 7. Вязкость
- 8. Вязкость
- 9. ВязкостьВ опыте И. Ньютона, в сосуде с
- 10. Вязкость
- 11. Вязкость
- 12. Вязкость
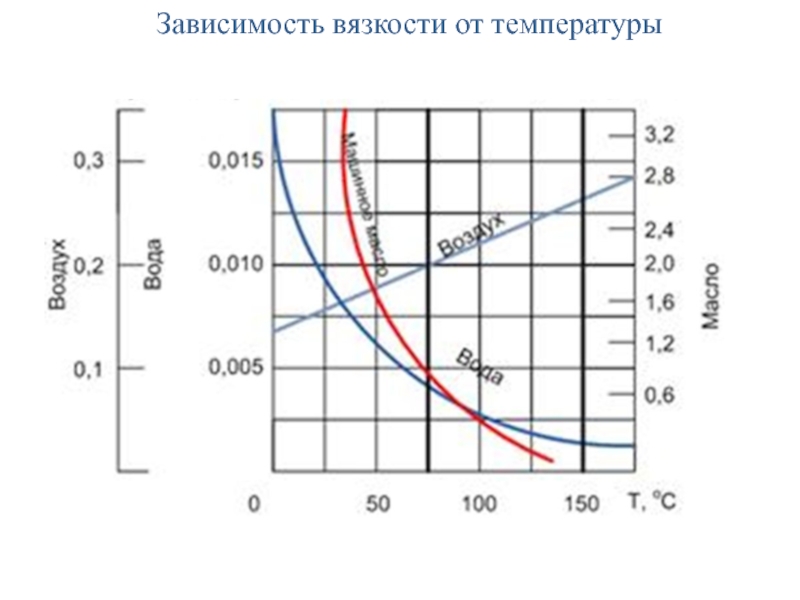
- 13. Зависимость вязкости от температуры
- 14. Вязкость
- 15. Вязкость
- 16. Вязкость
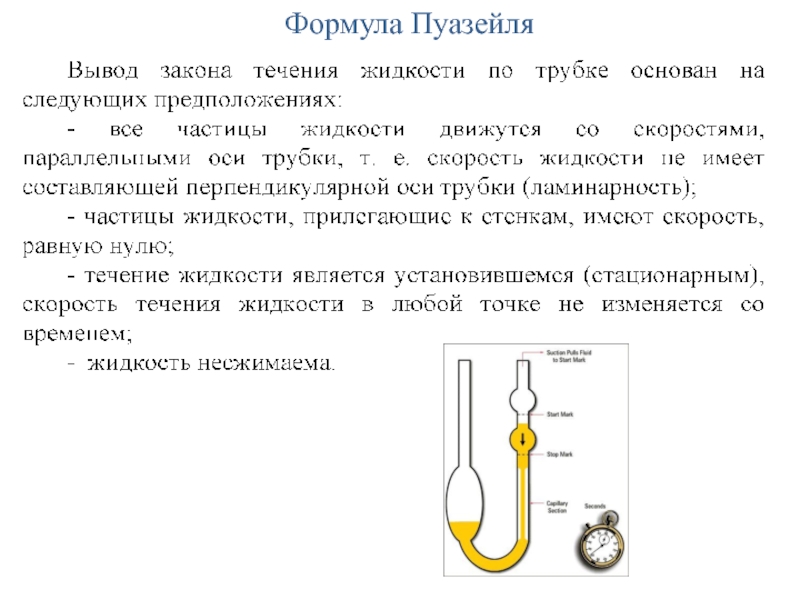
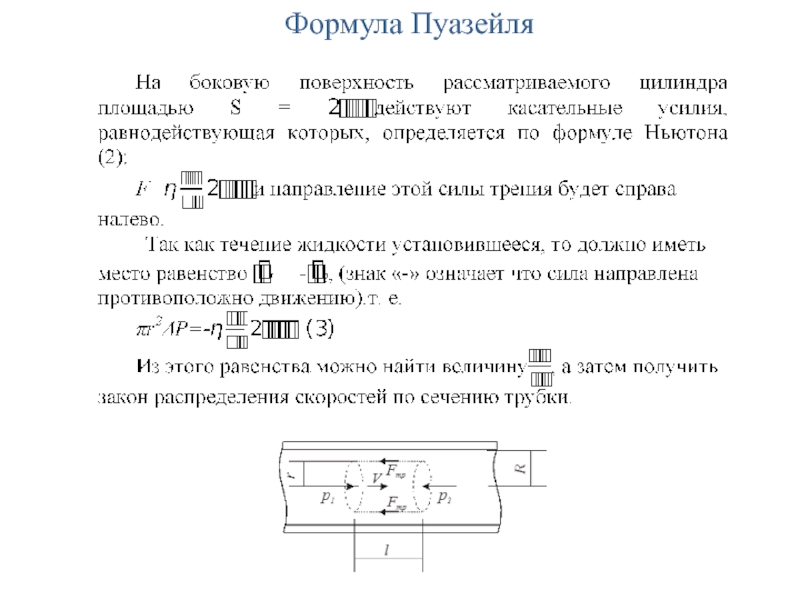
- 17. Формула Пуазейля
- 18. Формула Пуазейля
- 19. Формула Пуазейля
- 20. Формула Пуазейля
- 21. Формула Пуазейля
- 22. Формула Пуазейля
- 23. Формула Пуазейля
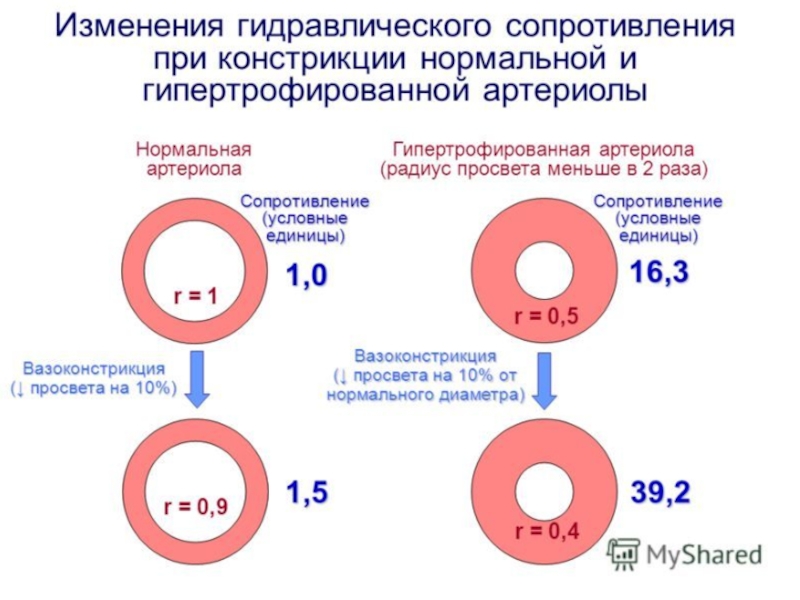
- 24. Гидравлическое сопротивление
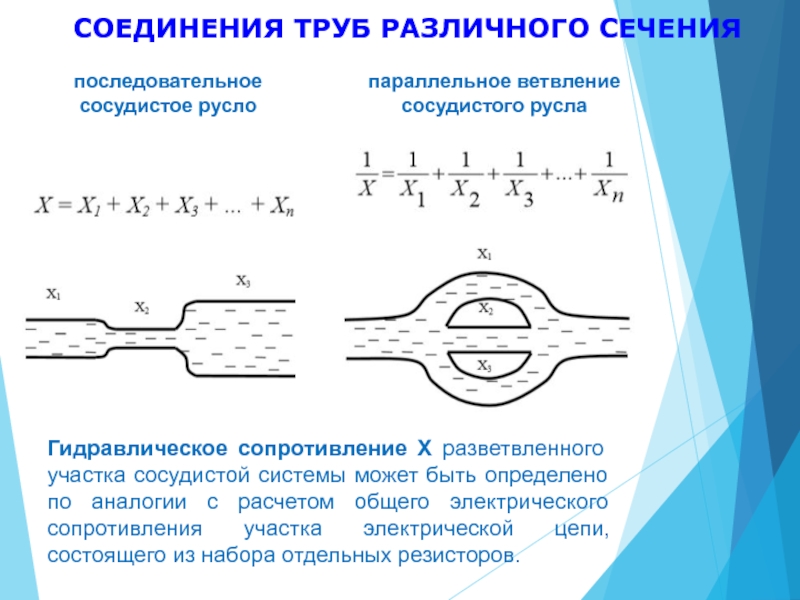
- 25. СОЕДИНЕНИЯ ТРУБ РАЗЛИЧНОГО СЕЧЕНИЯГидравлическое сопротивление X
- 26. Распределение давления при течении реальной жидкости по
- 27. Слайд 27
- 28. Характеристика движения крови по сосудам
- 29. Турбулентное течение. Число РейнольдсаЕсли скорость течения жидкости
- 30. Движение тела в жидкости. На тело движущееся
- 31. Движение тела в жидкости. На тело массой
- 32. Скорость осаждения тел в жидкости. (ρT -
- 33. Скорость осаждения тел в жидкости. Центрифугирование используется
- 34. Физические основы клинического метода измерения артериального давления.
- 35. Капиллярные явления Если жидкость налита в широкий
- 36. Капиллярные явления В узких трубочках, диаметр которых
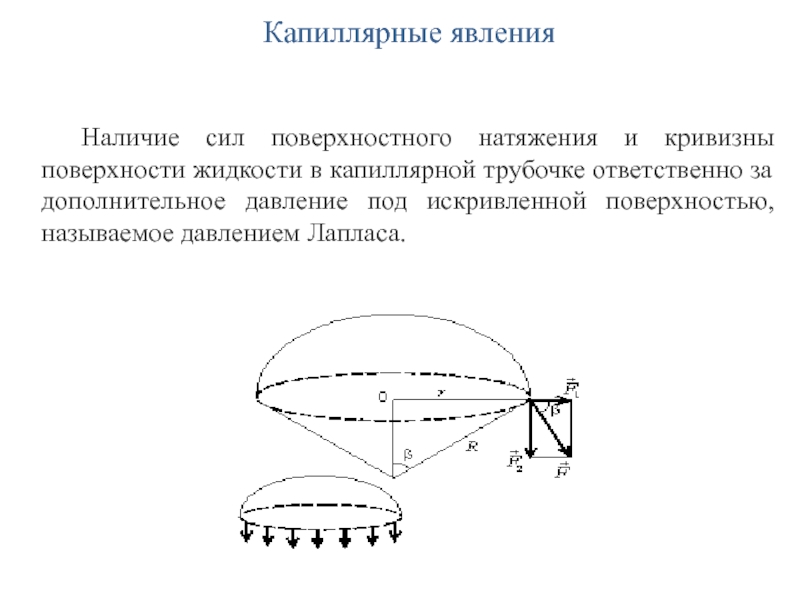
- 37. Капиллярные явления Наличие сил поверхностного натяжения и
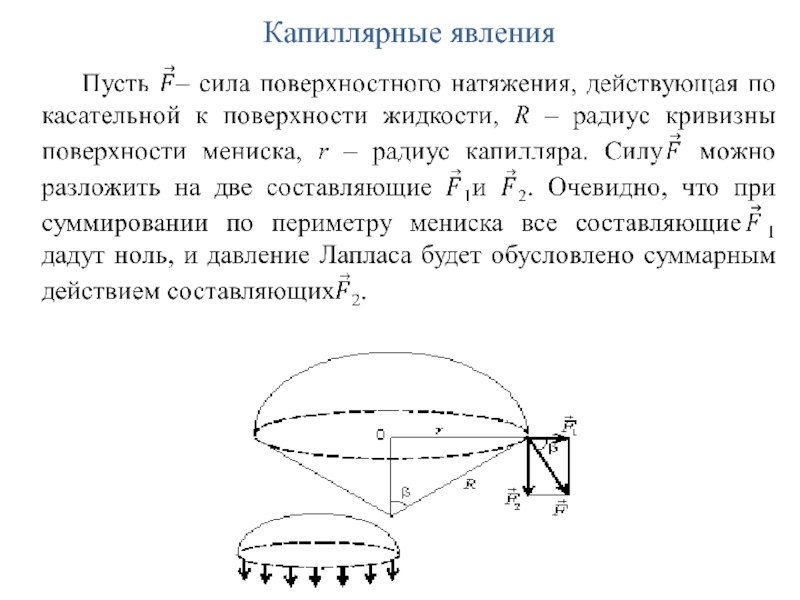
- 38. Капиллярные явления
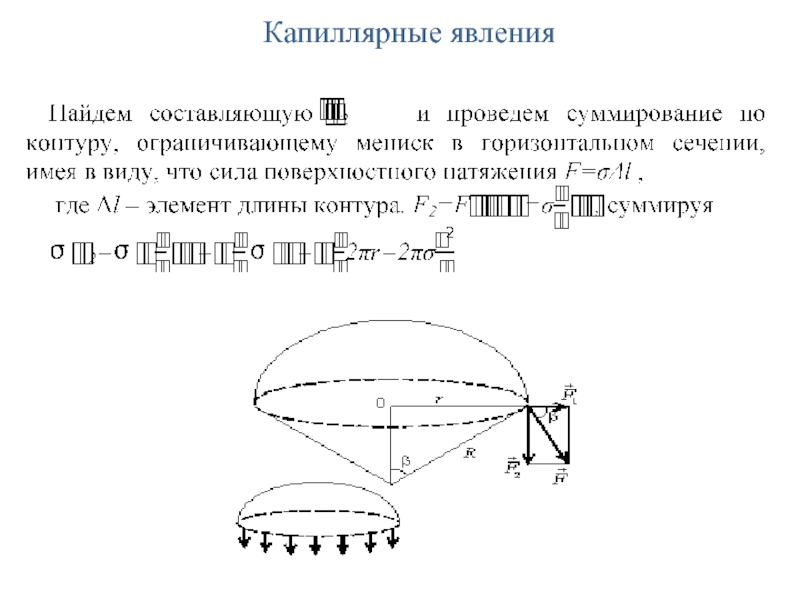
- 39. Капиллярные явления
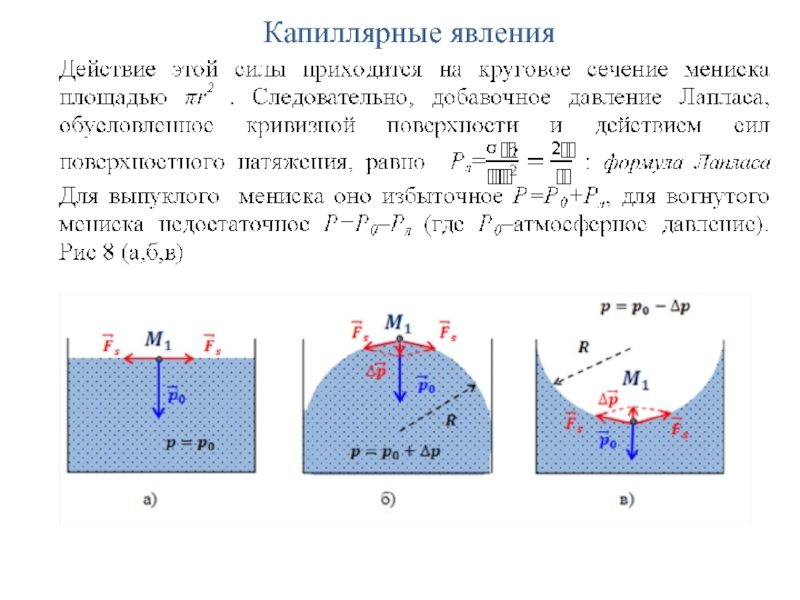
- 40. Капиллярные явления
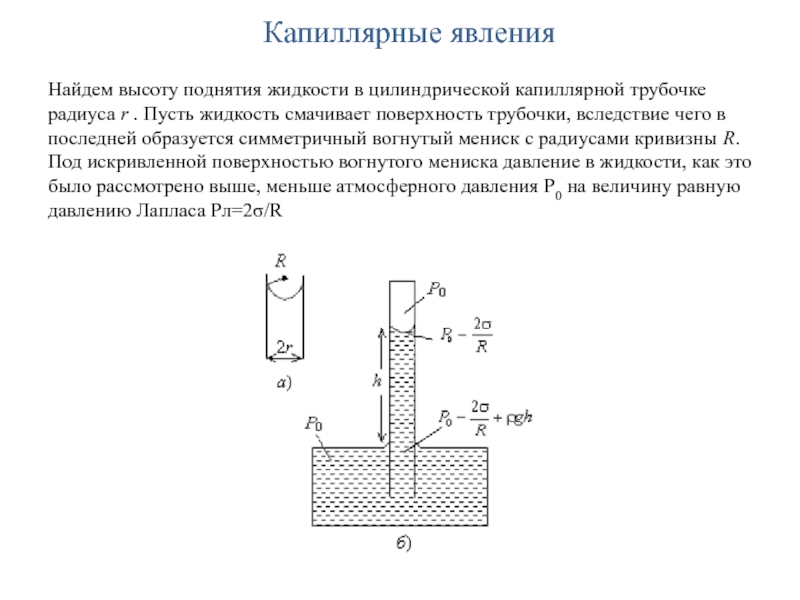
- 41. Капиллярные явления Найдем высоту поднятия жидкости в
- 42. Капиллярные явления Условие равновесия жидкости в капиллярной
- 43. Газовая эмболия Пока диаметр газового пузырька меньше
- 44. Спасибо за внимание!
- 45. Скачать презентанцию
Течения жидкостейЕсли течение плавное и слои жидкости скользят друг относительно друга, траектории разных частиц не пересекаются такое движение называется ламинарным. Турбулентное течение характеризуется наличием завихрений. Внутреннее трение при движении соседних слоев,
Слайды и текст этой презентации
Слайд 2Течения жидкостей
Если течение плавное и слои жидкости скользят друг относительно
друга, траектории разных частиц не пересекаются такое движение называется ламинарным.
Турбулентное течение характеризуется наличием завихрений. Внутреннее трение при движении соседних слоев, называемое вязкостью, здесь значительно больше чем при ламинарном течении. Будем считать что жидкости настолько мало сжимаемы что плотность их везде одинакова. При ламинарном течении наличием вязкости жидкости будем пренебрегать. Установившемся (стационарным) движением жидкости считается такое движение скорость течения которого в любой точке не изменяется со временем.Слайд 4Поток жидкости и уравнение неразрывности
Выберем достаточно малый промежуток времени Δt.
За этот промежуток времени объем жидкости V1 проходящий через поперечное
сечение S1 будет равен V1=S1l1 где l1 длина пути которая проходит выделенная частица за время Δt. Поскольку скорость жидкости через сечение S1: υ1= l1 /Δt то масса переносимой жидкости через поперечное сечение S1 за время Δt будет равна:Δm/Δt = ρ1V1/Δt = ρ1S1l1/Δt = ρ1S1υ1
Аналогично для сечения S2:
Δm/Δt = ρ1V1/Δt = ρ1S2l2/Δt = ρ1S2υ2
Поскольку перенос жидкости через стенки трубки отсутствует то масса переносимой жидкости не изменяется ρ1S1υ1 = ρ1S2υ2 и соответственно S1υ1 = S2υ2 Это выражение называется уравнением неразрывности.
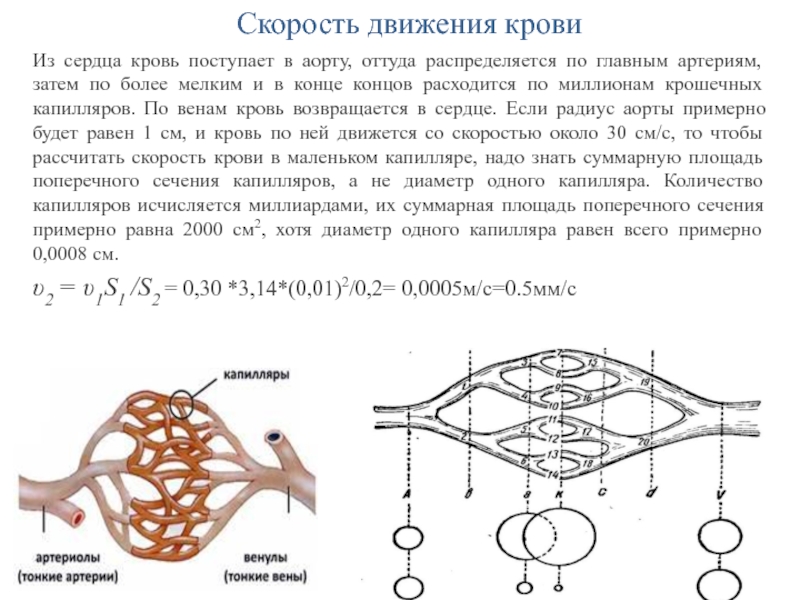
Слайд 5Скорость движения крови
Из сердца кровь поступает в аорту, оттуда распределяется
по главным артериям, затем по более мелким и в конце
концов расходится по миллионам крошечных капилляров. По венам кровь возвращается в сердце. Если радиус аорты примерно будет равен 1 см, и кровь по ней движется со скоростью около 30 см/с, то чтобы рассчитать скорость крови в маленьком капилляре, надо знать суммарную площадь поперечного сечения капилляров, а не диаметр одного капилляра. Количество капилляров исчисляется миллиардами, их суммарная площадь поперечного сечения примерно равна 2000 см2, хотя диаметр одного капилляра равен всего примерно 0,0008 см.υ2 = υ1S1 /S2 = 0,30 *3,14*(0,01)2/0,2= 0,0005м/с=0.5мм/c
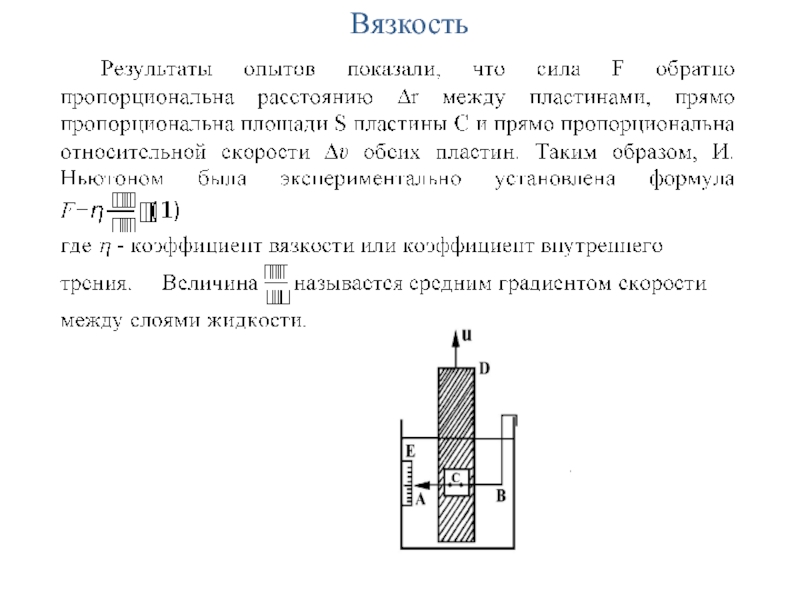
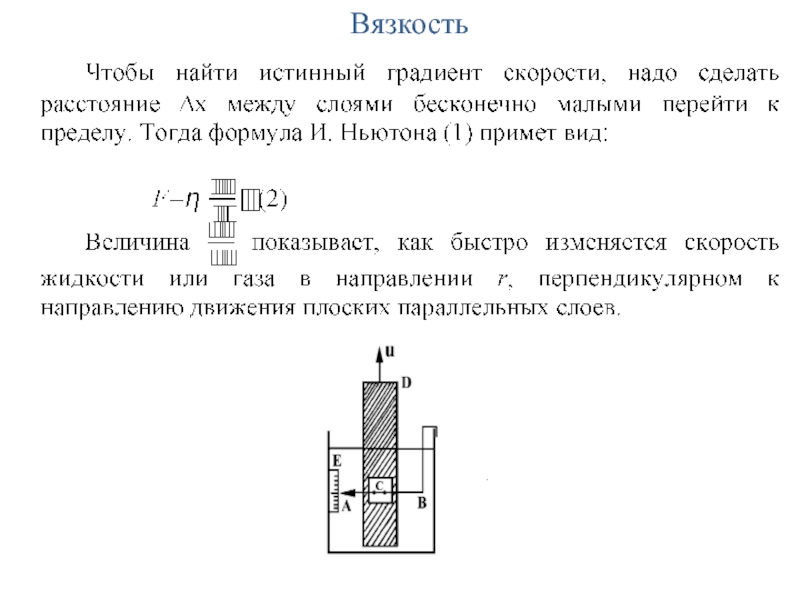
Слайд 9Вязкость
В опыте И. Ньютона, в сосуде с исследуемой жидкостью на
упругой горизонтальной узкой упругой проволоке (пружине) AB вертикально укреплена небольшая
пластина C площади S из материала, смачиваемого исследуемой жидкостью. На малом расстоянии r за ней помещается длинная пластина D. Если заставить пластину D двигаться вверх со скоростью υ, то благодаря внутреннему трению она приведет в движение прилегающие слои жидкости, которые в свою очередь будут действовать на пластину C. В результате пластина C испытает направленную вверх силу F и несколько сместится вверх из положения равновесия. По положению на шкале E конца пружины АВ можно определить величину силы F, если пружина была предварительно проградуирована.Слайд 25
СОЕДИНЕНИЯ ТРУБ РАЗЛИЧНОГО СЕЧЕНИЯ
Гидравлическое сопротивление X разветвленного участка сосудистой
системы может быть определено по аналогии с расчетом общего электрического
сопротивления участка электрической цепи, состоящего из набора отдельных резисторов.последовательное сосудистое русло
параллельное ветвление сосудистого русла
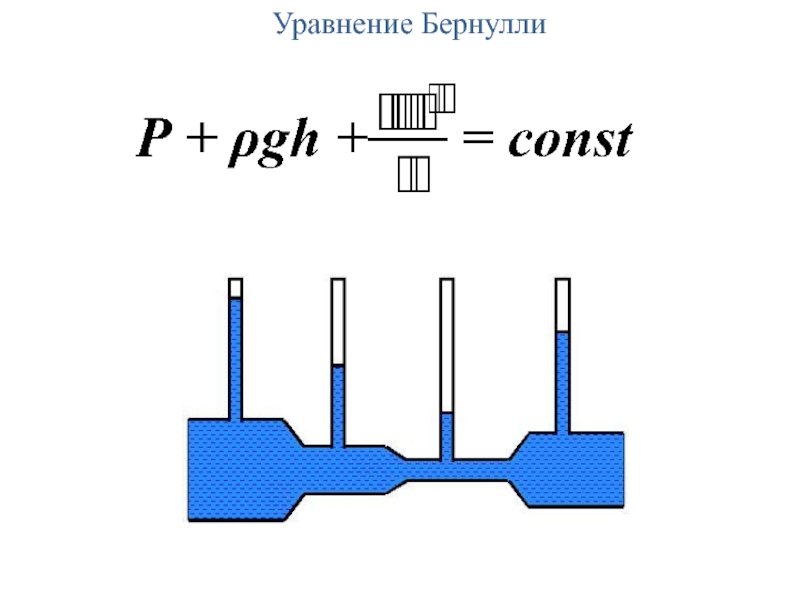
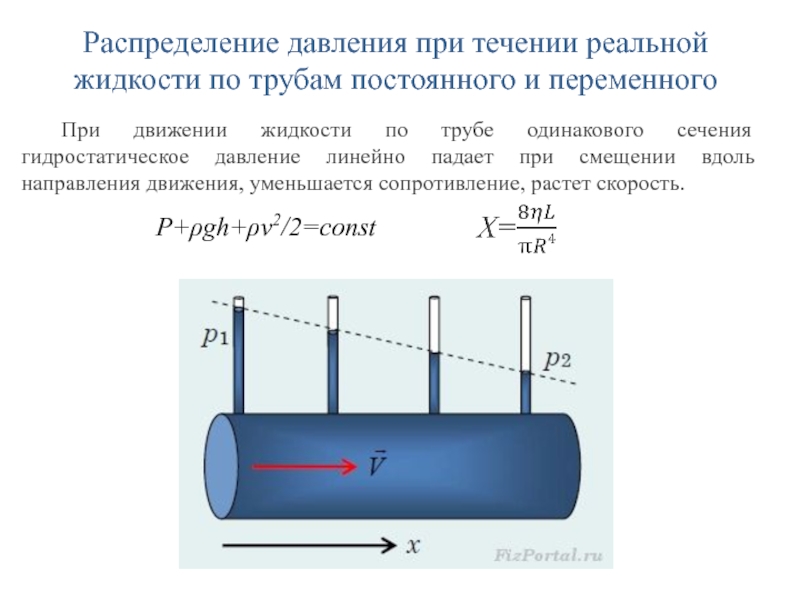
Слайд 26Распределение давления при течении реальной жидкости по трубам постоянного и
переменного
При движении жидкости по трубе одинакового сечения гидростатическое давление линейно
падает при смещении вдоль направления движения, уменьшается сопротивление, растет скорость.P+ρgh+ρν2/2=const
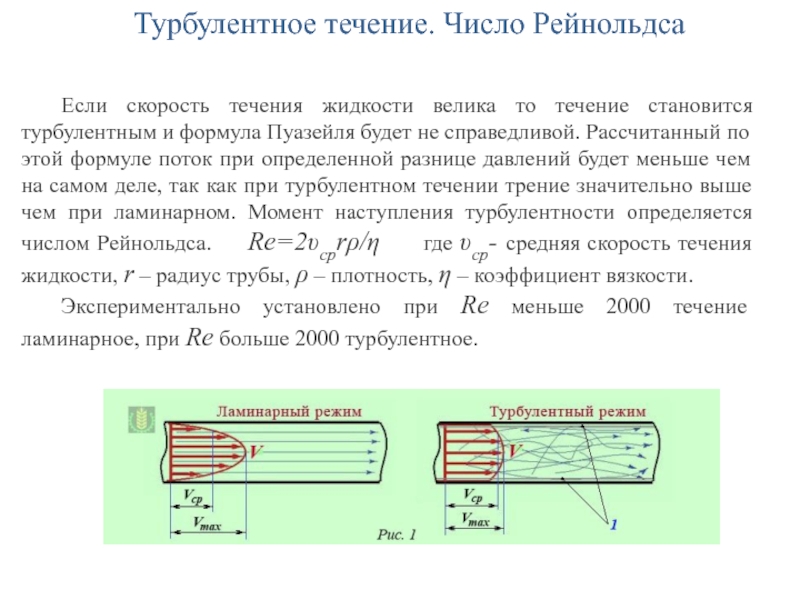
Слайд 29Турбулентное течение. Число Рейнольдса
Если скорость течения жидкости велика то течение
становится турбулентным и формула Пуазейля будет не справедливой. Рассчитанный по
этой формуле поток при определенной разнице давлений будет меньше чем на самом деле, так как при турбулентном течении трение значительно выше чем при ламинарном. Момент наступления турбулентности определяется числом Рейнольдса. Re=2υсрrρ/η где υср- средняя скорость течения жидкости, r – радиус трубы, ρ – плотность, η – коэффициент вязкости.Экспериментально установлено при Re меньше 2000 течение ламинарное, при Re больше 2000 турбулентное.
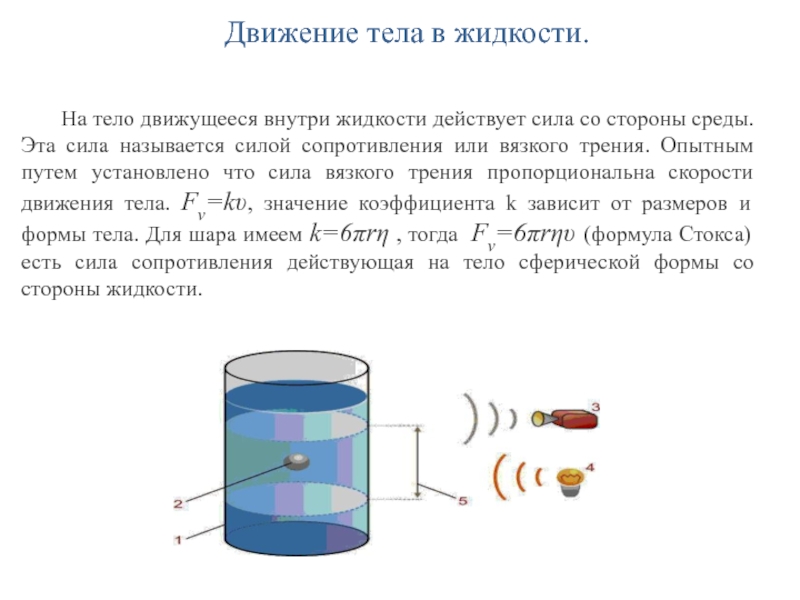
Слайд 30Движение тела в жидкости.
На тело движущееся внутри жидкости действует сила
со стороны среды. Эта сила называется силой сопротивления или вязкого
трения. Опытным путем установлено что сила вязкого трения пропорциональна скорости движения тела. Fv=kυ, значение коэффициента k зависит от размеров и формы тела. Для шара имеем k=6πrη , тогда Fv=6πrηυ (формула Стокса) есть сила сопротивления действующая на тело сферической формы со стороны жидкости.Слайд 31Движение тела в жидкости.
На тело массой m движущееся внутри жидкости
действуют несколько сил: сила тяжести FТ=mg=ρTVT g, выталкивающая сила FА=ρж
g VT, сила сопротивления среды (сила Стокса) Fv=6πrηυ. По второму закону Ньютона после проецирования сил на вертикальную ось получим:FТ - FА - Fv= ma или ρTVTg - ρжgVT - 6πrηυv= ma
(ρT - ρж )gVT - 6πrηυv= ma
Первый член уравнения (ρT - ρж )gVT - есть эффективный вес тела в жидкости. При падении тела вниз сила вязкого сопротивления возрастает пока она не сравняется с эффективным весом. При этом ускорение тела становится равным нулю и скорость перестает меняться.
Слайд 32Скорость осаждения тел в жидкости.
(ρT - ρж )gVT - 6πrηυv=
ma (ρT -
ρж )gVT - 6πrηυv= 0υv=(ρT - ρж )gVT /6πrη в общем случае υv=(ρT - ρж )gVT /k
Скорость осаждения микроскопических тел: макромолекул, других составных частей клеток очень мала. Ее можно увеличить с помощью центрифуги, поскольку в центрифуге на частицу действует такая сила, если бы ускорение свободного падения g увеличилось бы до ω2r.(где ω угловая скорость вращения центрифуги, r расстояние от частицы до оси вращения. Применительно к центрифуги последнее уравнение запишется так υv=(ρT - ρж ) ω2rVT /k .
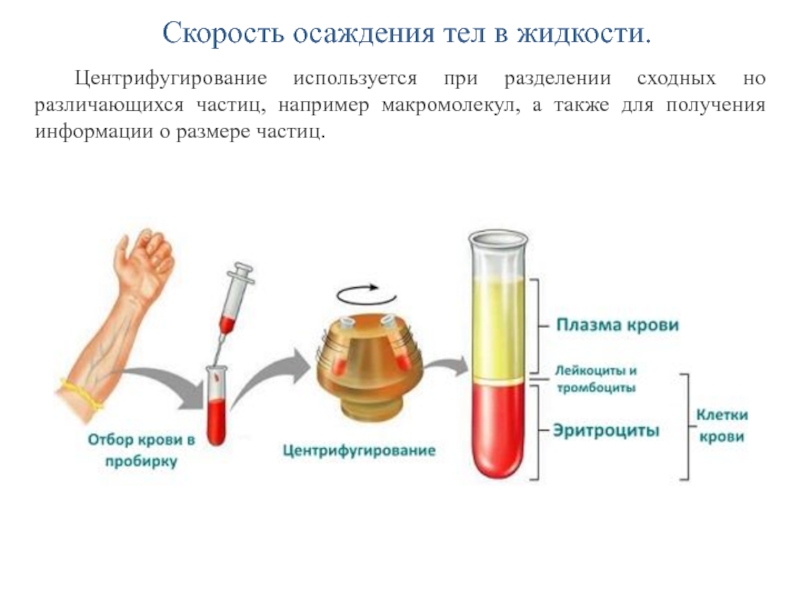
Слайд 33Скорость осаждения тел в жидкости.
Центрифугирование используется при разделении сходных но
различающихся частиц, например макромолекул, а также для получения информации о
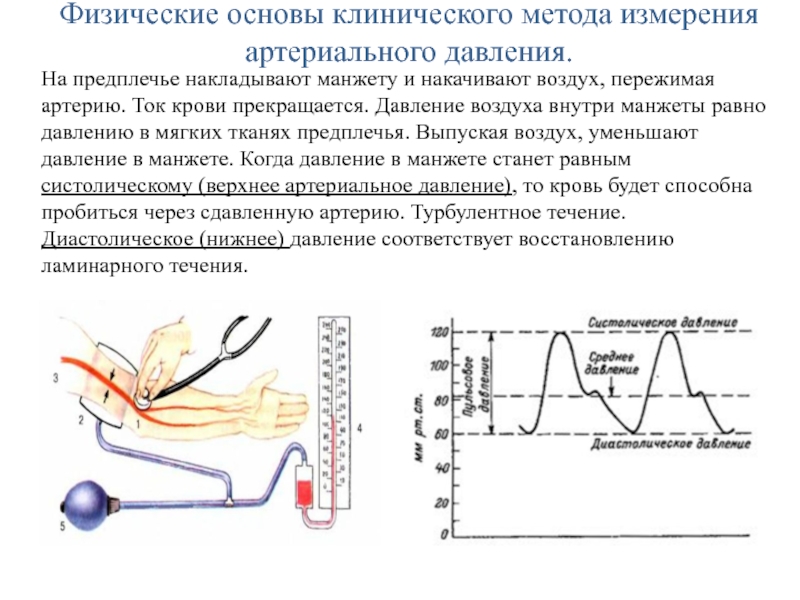
размере частиц.Слайд 34Физические основы клинического метода измерения артериального давления.
На предплечье накладывают манжету
и накачивают воздух, пережимая артерию. Ток крови прекращается. Давление воздуха
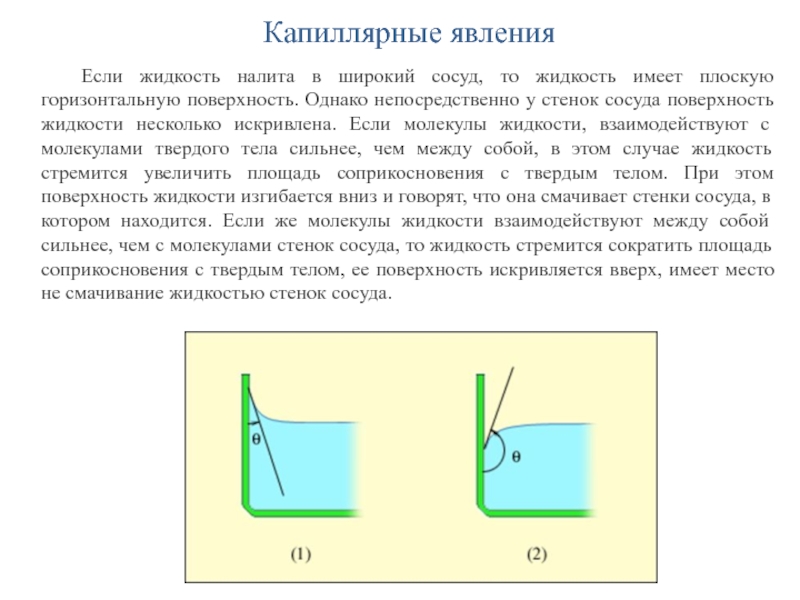
внутри манжеты равно давлению в мягких тканях предплечья. Выпуская воздух, уменьшают давление в манжете. Когда давление в манжете станет равным систолическому (верхнее артериальное давление), то кровь будет способна пробиться через сдавленную артерию. Турбулентное течение. Диастолическое (нижнее) давление соответствует восстановлению ламинарного течения.Слайд 35Капиллярные явления
Если жидкость налита в широкий сосуд, то жидкость имеет
плоскую горизонтальную поверхность. Однако непосредственно у стенок сосуда поверхность жидкости
несколько искривлена. Если молекулы жидкости, взаимодействуют с молекулами твердого тела сильнее, чем между собой, в этом случае жидкость стремится увеличить площадь соприкосновения с твердым телом. При этом поверхность жидкости изгибается вниз и говорят, что она смачивает стенки сосуда, в котором находится. Если же молекулы жидкости взаимодействуют между собой сильнее, чем с молекулами стенок сосуда, то жидкость стремится сократить площадь соприкосновения с твердым телом, ее поверхность искривляется вверх, имеет место не смачивание жидкостью стенок сосуда.Слайд 36Капиллярные явления
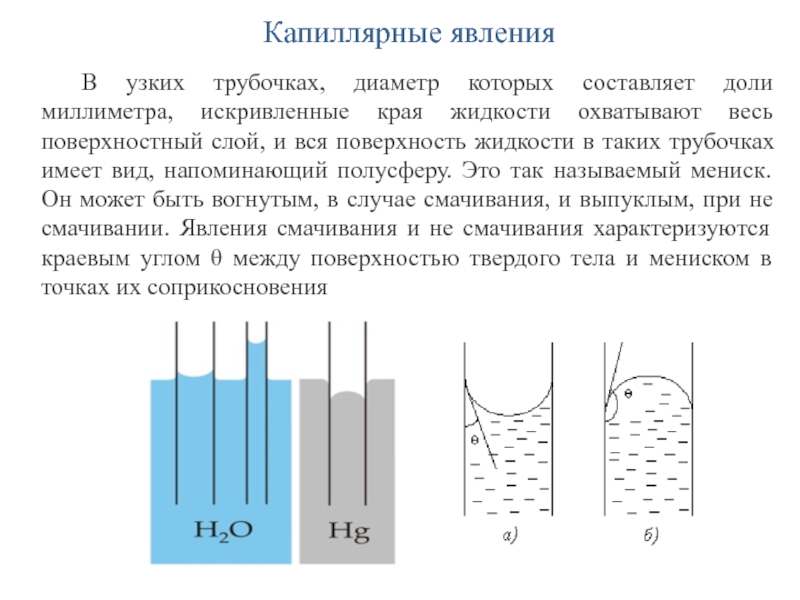
В узких трубочках, диаметр которых составляет доли миллиметра, искривленные
края жидкости охватывают весь поверхностный слой, и вся поверхность жидкости
в таких трубочках имеет вид, напоминающий полусферу. Это так называемый мениск. Он может быть вогнутым, в случае смачивания, и выпуклым, при не смачивании. Явления смачивания и не смачивания характеризуются краевым углом θ между поверхностью твердого тела и мениском в точках их соприкосновенияСлайд 37Капиллярные явления
Наличие сил поверхностного натяжения и кривизны поверхности жидкости в
капиллярной трубочке ответственно за дополнительное давление под искривленной поверхностью, называемое
давлением Лапласа.Слайд 41Капиллярные явления
Найдем высоту поднятия жидкости в цилиндрической капиллярной трубочке радиуса
r . Пусть жидкость смачивает поверхность трубочки, вследствие чего в
последней образуется симметричный вогнутый мениск с радиусами кривизны R. Под искривленной поверхностью вогнутого мениска давление в жидкости, как это было рассмотрено выше, меньше атмосферного давления Р0 на величину равную давлению Лапласа Pл=2σ/RСлайд 42Капиллярные явления
Условие равновесия жидкости в капиллярной трубочке определяется равенством
P0=P0-2σ/R+ρgh
где
ρ – плотность жидкости, h – высота ее поднятия в
трубочке, g – ускорение силы тяжести, отсюдаh=2σ/ρgR
Преобразуем это выражение, выразив радиус кривизны R мениска через радиус капилляра r.
r = RcosӨ, в итоге получаем: h=2σ cosӨ/ρgr
Это формула Жюрена
где r – радиус капилляра, Ө - краевой угол.
Для жидкости, которая полностью смачивает
стенки капилляра Ө=0, cosӨ =1
h=2σ/ρgr