Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производные функций. Правила дифференцирования. Дифференциал функции
Содержание
- 1. Производные функций. Правила дифференцирования. Дифференциал функции
- 2. Пусть функция у = f(x) определена на
- 3. Определение. Если существует
- 4. Если этот предел конечен, то производная называется
- 5. Пример. Найдем производную у = х2 на основании определения производной.Решение.Δy=(x+Δx)2-x2 = 2x.Δx + (Δx)2.Тогда:
- 6. Физический смысл - производная функции отражает скорость
- 7. Скорость (быстрота) протекания физических, химических, биологических процессов,
- 8. Геометрический смысл:Производная функции у = f(x) геометрически
- 9. Слайд 9
- 10. При этом если существует касательная, то существует
- 11. Слайд 11
- 12. Определение: Если приращение функции y = f(x)
- 13. Из последнего равенства следует, что Перейдя к пределу при Δх → 0, получим:
- 14. Итак, если y = f(x) дифференцируема в
- 15. Теорема 1 (необходимое условие дифференцируемости):Если функция y
- 16. Эти функции непрерывны, но не имеют производной
- 17. 1. Производная от постоянной величины равна нулю,
- 18. 2. Производная алгебраической суммы конечного числа функций
- 19. 3. Производная произведения двух функций определяется формулой:4. Производная частного от деления двух функций определяется формулой:
- 20. Производные от основных элементарных функций:
- 21. Слайд 21
- 22. Рассмотрим сложную функцию с одним промежуточным аргументом:
- 23. На основании определения производной имеемтак как предел равен произведению пределов.
- 24. Если учесть, что поскольку всякая дифференцируемая функция непрерывна, то получим, что
- 25. или, в других обозначениях,
- 26. Пример. Найти у', если: у = sin3
- 27. Предположим, что функция у = f(x) определена,
- 28. Для вывода можно воспользоваться правилом дифференцирования сложной
- 29. На основании правила дифференцирования сложной функции получаем:
- 30. Определение. Дифференциалом функции называется произведение производной этой
- 31. Как видно из определения, дифференциал функции существует
- 32. Рассмотрим следующий пример: Найдем приращение Δy функции
- 33. Рассмотрим малые приращения аргумента. Например, пусть при
- 34. Таким образом, дифференциал функции, в общем случае
- 35. При достаточно малых приращениях аргумента величина приращения
- 36. Рассмотрим график функции y = f(x). Геометрический смысл дифференциала.
- 37. Пусть через точку A (x,y), лежащую на
- 38. Поскольку углы FAE и FDC равны как
- 39. Учитывая, что катет АЕ = Δx, а
- 40. Рассмотрим функцию, равную своему аргументу: y =
- 41. Формулу дифференциала функции можно записать в виде:dy = y’dy,а формулу производной – в виде:
- 42. Таким образом, производная функции равна отношению дифференциала функции к дифференциалу ее аргумента.
- 43. Скачать презентанцию
Пусть функция у = f(x) определена на некотором промежутке, и пусть x0 - некоторая точка этого промежутка. Пусть Δx - приращение к значению аргумента такое, что (x0 + Δx) не выходит
Слайды и текст этой презентации
Слайд 1ЛЕКЦИЯ № 2
по дисциплине «Математика»
на тему: «Производные функций. Правила дифференцирования.
Дифференциал функции»
С.М. Кирова
Кафедра биологической и медицинской физики
Слайд 2
Пусть функция у = f(x) определена на некотором промежутке, и
пусть x0 - некоторая точка этого промежутка. Пусть Δx -
приращение к значению аргумента такое, что (x0 + Δx) не выходит за пределы упомянутого промежутка, а Δy == f(x0 + Δx) — f(x0) — соответствующее приращение функции.
1. Понятие производной. Правила дифференцирования. Производные от основных элементарных функций.
Слайд 3Определение. Если существует
,
то этот предел называется производной от функции у =
f(x) по переменной х в точке x0 (обозначения: или у'х). Итак:
Слайд 4Если этот предел конечен, то производная называется конечной, если же
этот предел бесконечен, то у'х — бесконечная производная.
Если конечная производная
существует в каждой точке некоторого множества, то она оказывается функцией от х , заданной на этом множестве.
Слайд 5Пример. Найдем производную у = х2 на основании определения производной.
Решение.
Δy=(x+Δx)2-x2
= 2x.Δx + (Δx)2.
Тогда:
Слайд 6
Физический смысл - производная функции отражает скорость изменения функции при
изменении ее аргумента.
Например, если x = f(t) есть уравнение прямолинейного
движения точки, то производная dx/dt представляет собой мгновенную скорость точки в момент времени t.
Геометрический и физический смысл производной
Слайд 7Скорость (быстрота) протекания физических, химических, биологических процессов, например скорость охлаждения
тела, скорость химической реакции и т.п., также выражается при помощи
производной.Например, скорость охлаждения тела равна производной температуры тела по времени:
Скорость химической реакции есть производная массы образующегося вещества по времени: .
и т.д.
Слайд 8
Геометрический смысл:
Производная функции у = f(x) геометрически представляет собой угловой
коэффициент касательной к графику этой функции в точке с абсциссой
х (тангенс угла наклона касательной к оси 0X).
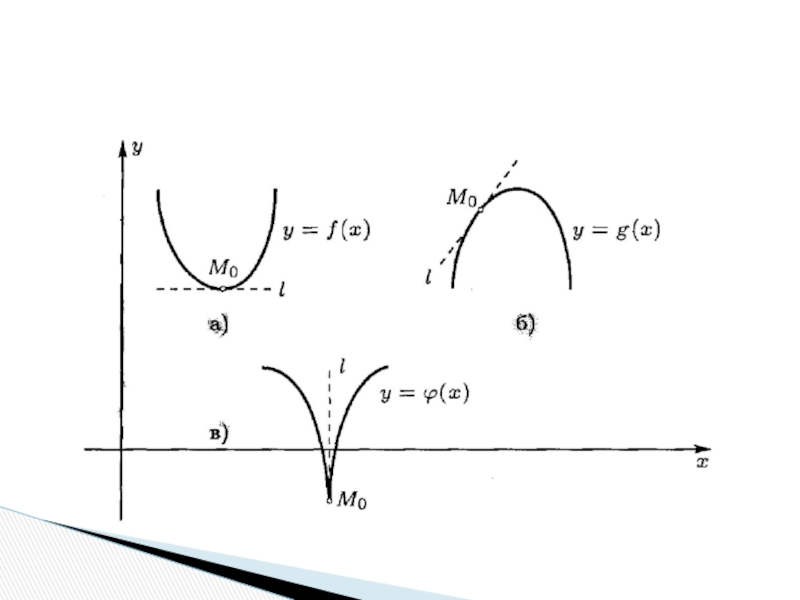
Слайд 10
При этом если существует касательная, то существует и производная, и
наоборот. Случаю касательной, не параллельной оси OY, отвечает конечная производная,
параллельной оси OY – бесконечная производная.
Слайд 12
Определение: Если приращение функции
y = f(x) в точке х
можно представить в форме
Δy = AΔx + αΔx,
где А
не зависит от Δх и α – бесконечно малое в точке х, то эта функция называется дифференцируемой в точке x.
Дифференцируемость функции в точке
Слайд 14Итак, если y = f(x) дифференцируема в точке х, то
приращение этой функции можно представить в виде
где α –
бесконечно малое в точке х.Отсюда следует, что если функция y = f(x) дифференцируема в точке х, то она обладает в этой точке конечной производной.
Можно показать, что справедливо и обратное утверждение.
Слайд 15Теорема 1 (необходимое условие дифференцируемости):
Если функция y = f(x) дифференцируема
в точке х, то она непрерывна в ней.
Обратное утверждение неверно,
то есть из непрерывности не следует дифференцируемость. Рассмотрим две функции:
Связь дифференцируемости и непрерывности
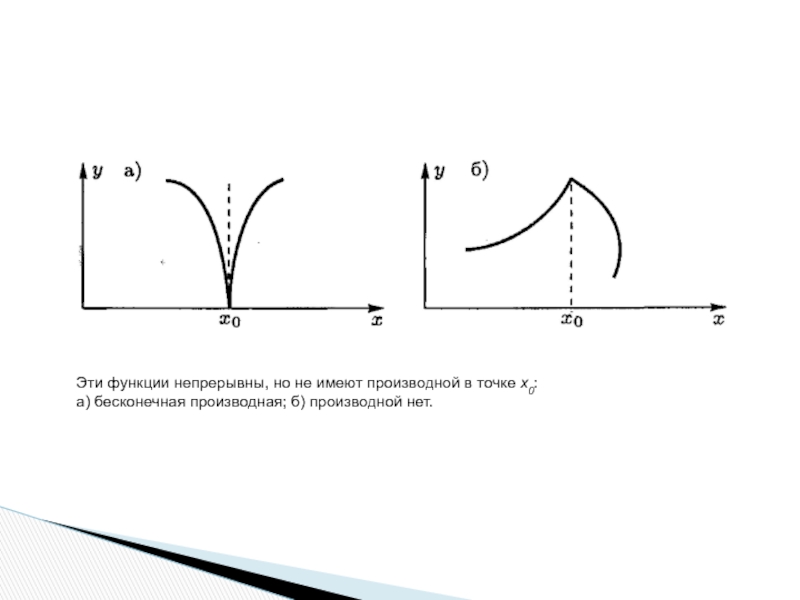
Слайд 16
Эти функции непрерывны, но не имеют производной в точке x0:
а) бесконечная производная; б) производной нет.
Слайд 17
1. Производная от постоянной величины равна нулю, т.е. если y
= C, то y’ = 0:
Доказательство. По определению производной y’
= Очевидно, что Δу = 0, следовательно Δу/Δх= 0; у'= 0.
Правила дифференцирования:
Слайд 182. Производная алгебраической суммы конечного числа функций равна сумме производных
слагаемых:
(u + v + w + ...)' = u '
+ v ' + w ' + ...Доказательство. Очевидно,
Δ(u + v + w + ...) = Δи + Δv + Δw + ... Остается поделить обе части этого равенства на Δx, перейти к пределу при
Δx → 0 и воспользоваться тем, что предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых.
Слайд 193. Производная произведения двух функций определяется формулой:
4. Производная частного от
деления двух функций определяется формулой:
Слайд 22
Рассмотрим сложную функцию с одним промежуточным аргументом: у=f(u),u =φ(х), предполагая
при этом, что функция у дифференцируема по аргументу u, а
функция u дифференцируема по аргументу х. Требуется вывести правило дифференцирования этой сложной функции.
2. Дифференцирование сложной функции.
Слайд 26Пример.
Найти у', если: у = sin3 5х.
Производную этой сложной
функции будем находить по формуле
Тогда
Слайд 27Предположим, что функция у = f(x) определена, монотонна и дифференцируема
в некоторой области, причем производная dy/dx нигде не равна нулю.
Наша функция у = f(x) имеет обратную функцию х = φ (у), и нам надо получить правило дифференцирования этой функции.
Производная обратной функции.
Слайд 28Для вывода можно воспользоваться правилом дифференцирования сложной функции с одним
промежуточным аргументом.
Согласно представлениям о сложной функции функцию у можно
рассматривать как сложную функцию от самой себя с промежуточным аргументом х: у = f(x), х = φ(у).
Слайд 29На основании правила дифференцирования сложной функции получаем:
Поскольку
= 1, получаем правило дифференцирования обратной функции:
Слайд 30
Определение. Дифференциалом функции называется произведение производной этой функции на приращение
ее аргумента:
3. Дифференциал функции: определение, геометрический смысл.
Слайд 31Как видно из определения, дифференциал функции существует лишь для дифференцируемых
функций, то есть функций, имеющих производную.
Дифференциал функции прямо пропорционален приращению
аргумента Δx (линеен относительно приращения аргумента функции).
Слайд 32Рассмотрим следующий пример:
Найдем приращение Δy функции y =x2 и
дифференциал этой функции:
Δy = (x + Δx)2 – x2 =
x2 + 2xΔx + (Δx)2 – x2 = 2xΔx + (Δx)2dy = 2xΔx
Из сравнения этих выражений видно, что приращение функции отличается от дифференциала функции на величину квадрата приращения аргумента (Δx)2.
Связь между дифференциалом функции и приращением функции:
Слайд 33Рассмотрим малые приращения аргумента. Например, пусть при x = 1
приращение аргумента равно 0,01. В этом случае первое слагаемое в
приращении функции (равное величине дифференциала) составит 0,02, а второе слагаемое – всего 0,0001, т.е. в 200 раз меньше.
Слайд 34
Таким образом, дифференциал функции, в общем случае отличаясь от приращения
функции, представляет собой главную часть этого приращения, линейную относительно приращения
аргумента. В этом заключается аналитический смысл дифференциала.
Слайд 35
При достаточно малых приращениях аргумента величина приращения функции приближенно равна
дифференциалу этой функции: Δy ≈ dy, причем погрешность этого приближенного
равенства тем меньше, чем меньше приращение Δx аргумента.
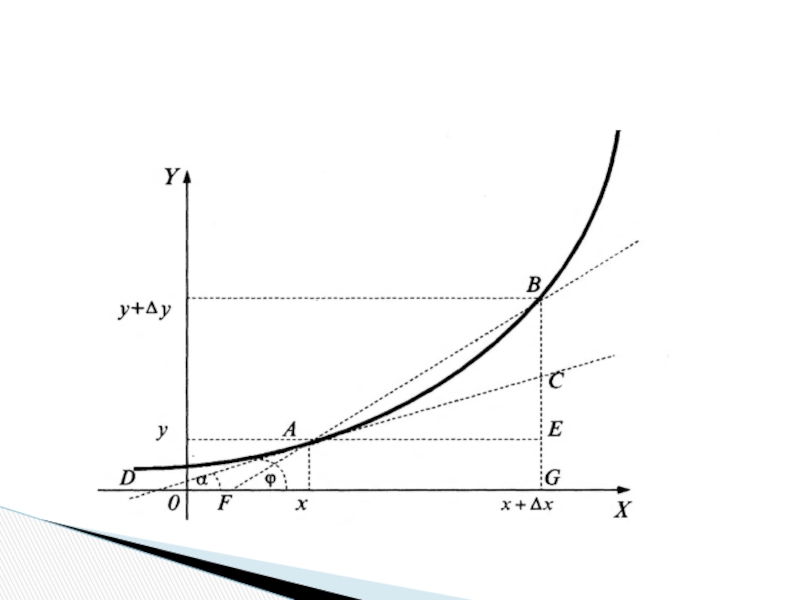
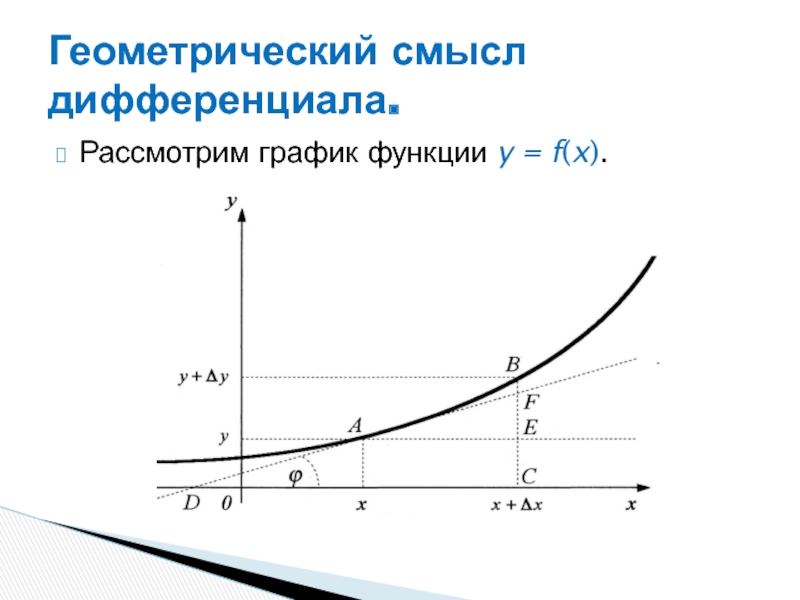
Слайд 37Пусть через точку A (x,y), лежащую на кривой графика функции,
проведена касательная DF, образующая угол FDC = φ с положительным
направлением оси 0X. Пусть точка B (x + Δx; y + Δy) также принадлежит данной кривой. Точка F лежит на пересечении линии BC, параллельной оси 0Y, и касательной DF.
Слайд 38
Поскольку углы FAE и FDC равны как соответственные при пересечении
параллельных прямых АЕ и DC прямой DF, то угол FAE
прямоугольного треугольника AFE также равен φ. Из этого треугольника для катета FE получаем:FE = AE•tgφ.
Слайд 39Учитывая, что катет АЕ = Δx, а из геометрического смысла
производной следует, что tgφ = y’, то из этого равенства
имеем:FE = y’•Δx = dy.
Дифференциал функции y = f(x) в точке с абсциссой x равен приращению ординаты касательной, проведенной к графику функции в этой точке, при переходе из данной точки в точку с абсциссой x + Δx.
Слайд 40
Рассмотрим функцию, равную своему аргументу: y = x.
Тогда дифференциал функции
равен дифференциалу аргумента:
dy =y’•Δx = 1•Δx = Δx
Таким образом, дифференциал
аргумента равен приращению аргумента.
Дифференциал аргумента функции
Слайд 41
Формулу дифференциала функции можно записать в виде:
dy = y’dy,
а формулу
производной – в виде:
Слайд 42
Таким образом, производная функции равна отношению дифференциала функции к дифференциалу
ее аргумента.
