Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Простейшие задачи квантовой механики. Линейный гармонический осциллятор
Содержание
- 1. Простейшие задачи квантовой механики. Линейный гармонический осциллятор
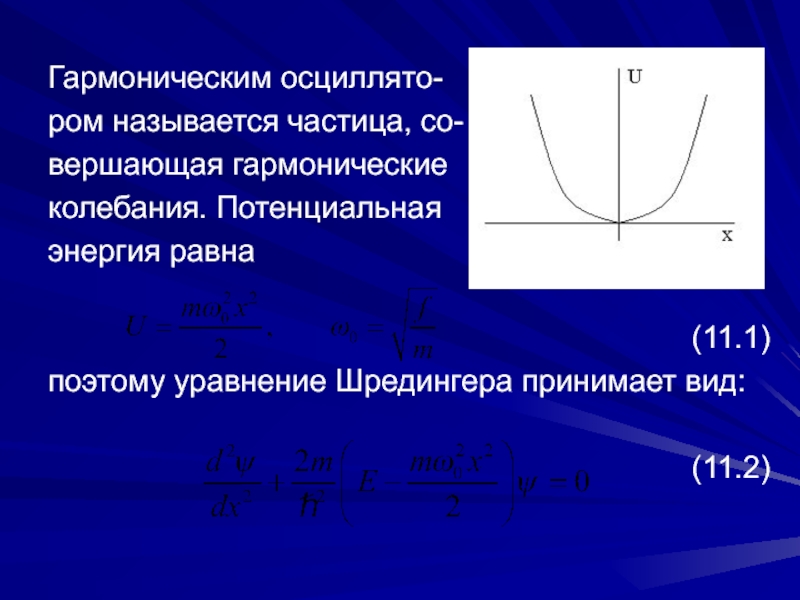
- 2. Гармоническим осциллято-ром называется частица, со-вершающая гармоническиеколебания. Потенциальнаяэнергия равна(11.1)поэтому уравнение Шредингера принимает вид:(11.2)
- 3. Качественно задача подобна рассмотренной вы-ше задаче о
- 4. Будем искать решение в виде(11.5)Тогда для функции
- 5. Подставим (11.7) в (11.6):Приравнивая нулю сумму коэффициентов
- 6. Отсюда и из формулы (11.3) находим энергию
- 7. Рекуррентная формула (11.8) позволяет последо-вательно вычислить все
- 8. Коэффициенты Cn находятся из условия норми-ровки:Вычисления дают
- 9. Скачать презентанцию
Гармоническим осциллято-ром называется частица, со-вершающая гармоническиеколебания. Потенциальнаяэнергия равна(11.1)поэтому уравнение Шредингера принимает вид:(11.2)
Слайды и текст этой презентации
Слайд 1Физика атома, атомного ядра и элементарных частиц
11 (2). Простейшие задачи
квантовой механики. Линейный гармонический осциллятор
Слайд 2Гармоническим осциллято-
ром называется частица, со-
вершающая гармонические
колебания. Потенциальная
энергия равна
(11.1)
поэтому уравнение Шредингера
принимает вид:
(11.2)
Слайд 3Качественно задача подобна рассмотренной вы-ше задаче о движении частицы в
потенциаль-ной яме, однако здесь имеется особенность, из-за которой задача довольно
сильно услож-няется: в пределах ямы потенциальная энергия не имеет постоянного значения, а изменяется по параболическому закону.Обозначим: (11.3)
Тогда уравнение Шредингера принимает вид:
(11.4)
Слайд 4Будем искать решение в виде
(11.5)
Тогда для функции v получаем следующее
уравнение:
(11.6)
Будем искать функцию v в виде бесконечного степенного ряда:
(11.7)
Для того,
чтобы решение не обратилось в беско-нечность, коэффициенты этого ряда надо подо-
брать так, чтобы они были равны нулю, начиная с
некоторого номера n+1. (Другими словами, беско-
нечный ряд должен превратиться в полином сте-
пени n).
Слайд 5Подставим (11.7) в (11.6):
Приравнивая нулю сумму коэффициентов при оди-
наковых степенях,
получаем следующие рекуррен-
тные соотношения для коэффициентов ak:
(11.8)
Как видно из этого
соотношения, для того, чтобы an ≠ 0, а an+2 = 0, необходимо, чтобыλn = 2n+1 (11.9)
Слайд 6Отсюда и из формулы (11.3) находим энергию ос-циллятора:
(11.10)
в частности, при
n = 0 минимальная энергия ос-циллятора не равна нулю:
(11.11)
что согласуется
с соотношениями неопределен-ности. Энергия E0 называется "нулевой энер-гией"; она не исчезает даже когда температура стремится к абсолютному нулю.
Слайд 7Рекуррентная формула (11.8) позволяет последо-вательно вычислить все члены ряда. Функцию
v можно теперь записать в виде:
если n четное
если n нечетное
Эти
полиномы называются полиномами Эрмита и обозначаются . Таким образом, волно-вая функция Ψn, принадлежащая собственному значению En, выражается формулой(11.12)
Слайд 8Коэффициенты Cn находятся из условия норми-ровки:
Вычисления дают следующий результат:
(11.13)
В частности,
для нулевого состояния собственная функция имеет вид:
