Слайд 1Теория вероятностей и математическая статистика
Проверка параметрических гипотез
ЛЕКЦИЯ 15
Слайд 2Общая схема проверки параметрических гипотез
1.Сформулировать статистическую
параметрическую модель, нулевую и
альтернативную гипотезы, задать уровень
значимости α.
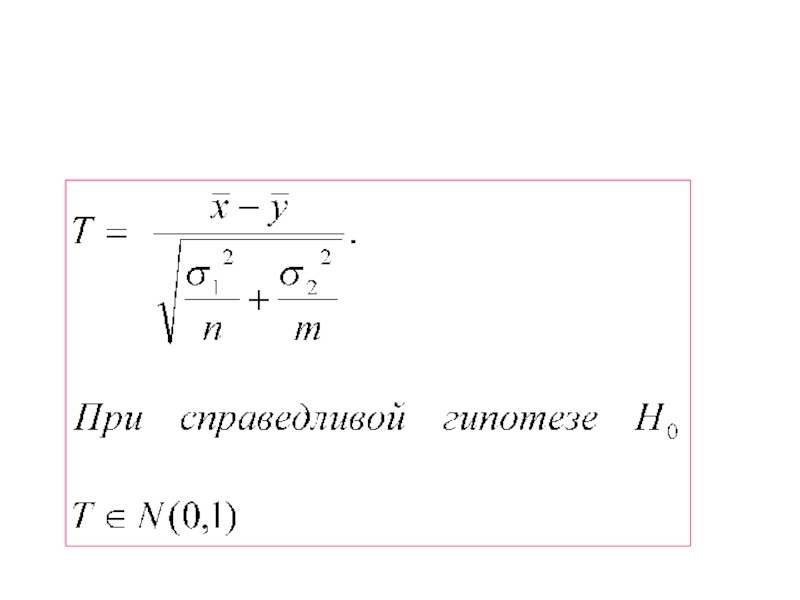
2. Выбрать статистику Т, такую,
что она сама
зависит от параметра θ, а ее распределение
от θ не зависит, и различается при H0 и при H1.
3. Найти критическую область V.
Слайд 3
4. Рассчитать по выборке значение ст –ки Тв.
5. Если Тв
попадает в критическую область V,
то нулевая гипотеза отвергается (в
пользу
альтернативной). Если Тв не попадает в
критическую область V, то нулевая гипотеза не
отвергается.
6. Сформулировать ответ в терминах вопроса.
Замечание. Гипотеза H0 отвергается или не отвергается с уровнем значимости α.
Слайд 4Пример
Автомат производит шарики диаметра 10 мм,
σ=0,3 мм. Выборочному контролю
были
подвергнуты 100 случайно взятых шариков.
Оказалось, что средний диаметр равен 10,06
мм. Можно ли считать это отклонение
случайным, или следует признать, что автомат
производит нестандартную продукцию?
Слайд 5Решение. N=100, a0=10, a1=10,06, σ=0,3
Модель: N(θ,σ). (Далее будем неизвестный параметр
θ обозначать, как обычно, a.)
H0: a = a 0,
H1: a > a0 .
α=0,05.
Слайд 6
3. Критическая область V =(t*,+∞), где
t*=u1 –α/2 (квантиль нормального
распределения порядка 1 –α/2). Область правосторонняя, поскольку в случае, когда
справедлива H1, распределение статистики T сместится вправо.
Слайд 7
3. (Продолжение).
α =0,05; 1 –α =0,95. u1 –α/2=1,64.
Т.о., критическая область
V =(1,64;+∞).
4.
Слайд 8
5. Тв попадает в критическую область V (поскольку 2>1,64). Следовательно,
с уровнем значимости α =0,05 нулевая гипотеза H0 отвергается (в
пользу
альтернативной H1).
6. Ответ. Отклонение нельзя считать
случайным, следует признать, что автомат
производит нестандартную продукцию.
Слайд 9Проверка гипотез о параметрах
нормального распределения
Гипотезы о параметрах одного распределения
(одна выборка).
Гипотеза о дисперсии.
(X1,, X2,...,Xn)€, N(a,θ), то
есть параметр σ не известен.
H0: σ = σ0.
Слайд 10Гипотеза о дисперсии. H0: σ = σ0.
Слайд 11H0: σ2 = 163; H1: σ2 ≠ 163.
Пусть
уровень значимости α = 0,05.
Sисп = 12,75
σ = 12
Tв. = 112 ∙ 162,57/163= 111,705
χ2 0,025= 84,6036 χ2 0,975 = 143,1801
T в. не принадлежит критической области, а значит гипотеза Но не отвергается (с доверительной вероятностью 0,95).
Пример
Слайд 12Гипотеза о среднем. H0: a = a0.
1) (X1,, X2,...,Xn)
€, N(θ1, σ), то есть параметр σ известен, а параметр
a не известен.
Слайд 13Пример
H0: a = 95; H1: a ≠ 95
Пусть
уровень значимости α = 0,05.
σ = 12
Xср = 94,64434
Tв.
= ((94,64434-95) ∙1131/2 )/ (12) = - 0,315
U0,025= - 1,96 U0,975 = 1,96
Tв. не принадлежит критической области, а значит гипотеза Но не отвергается (с доверительной вероятностью 0,95).
Слайд 14Гипотеза о среднем. H0: a = a0.
2) (X1,, X2,...,
Xn) € N(θ1,θ2), то есть оба параметра неизвестны.
Слайд 15Пример
H0: a = 95; H1: a ≠ 95
Пусть
уровень значимости α = 0,05.
Sисп = 12,75
Xср = 94,64434
Tв.
= ((94,64434-95) ∙1131/2) / (12,75) = - 0,297
T0,025= - 1,98 T0,975 = 1,98
Tв. не принадлежит критической области, а значит гипотеза Но не отвергается (с доверительной вероятностью 0,95).
Слайд 16 Гипотезы о параметрах двух распределений (две независимые выборки).
Гипотеза
о дисперсии. H0: σ1 = σ2.
(X1,, X2,..., Xn)
€ N(θ1,θ2),
(Y1,, Y2,..., Ym) € N(θ′1,θ2 ′), то есть параметры не известны.
Слайд 17Гипотеза о дисперсии. H0: σ1 = σ2.
Критерий Фишера
Слайд 18Гипотеза о среднем. H0: a1 = a2.
1) (X1,, X2,...,
Xn) € N(θ,σ1),
(Y1,, Y2,..., Ym) € N(θ,σ2),
то есть параметры σ известны.
Слайд 20
Гипотеза о среднем. H0: a1 = a2.
2) (X1,, X2,...,
Xn) € N(θ1,θ2),
(Y1,, Y2,..., Ym) € N(θ′1,θ2
′), то есть параметры σ неизвестны, но гипотеза о их равенстве не отвергается.
Слайд 21Гипотеза о среднем. H0: a1 = a2.
Критерий Стьюдента
Слайд 22Критерий Стьюдента для парных выборок
Гипотеза о среднем. H0: a1
= a2.
(X1,, X2,..., Xn) € N(θ1,θ2), (Y1,, Y2,..., Yn) €
N(θ′1,θ2 ′)
Xi и Yi связаны между собой (пара).
Перейдем к разностям di = Xi и Yi, для разностей гипотеза формулируется так:
H0: d0 = 0.
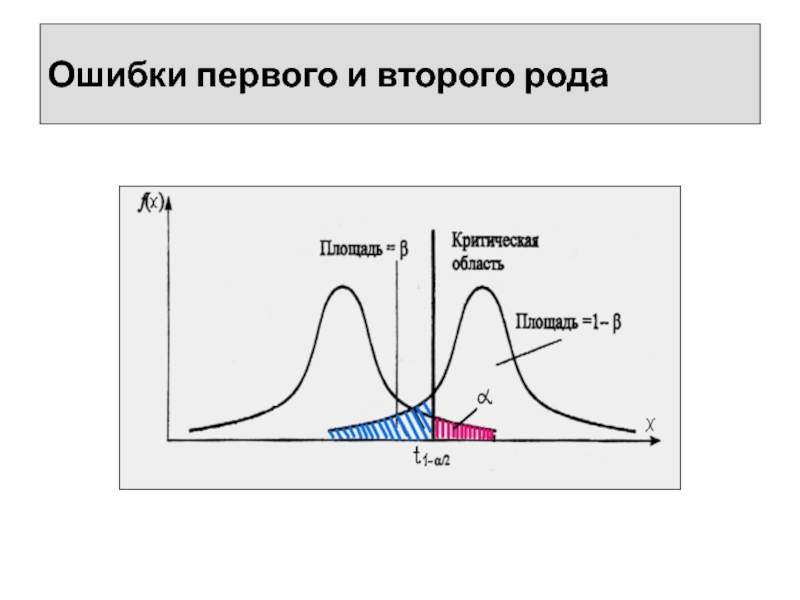
Слайд 24Ошибки первого и второго рода
Существует два рода ошибок, которые можно
сделать при проверке гипотез. Во –первых, можно ошибочно отвергнуть H0
(например, забраковать партию шариков). Вероятность совершить такую ошибку обычно называется вероятностью ошибки первого рода (альфа). Вторая ошибка, которую можно сделать, –ошибочно не отвергнуть H0 (посчитать, что шарики стандартны), когда на самом деле они нестандартны. Вероятность этой ошибки обычно называется вероятностью ошибки второго рода (бета).
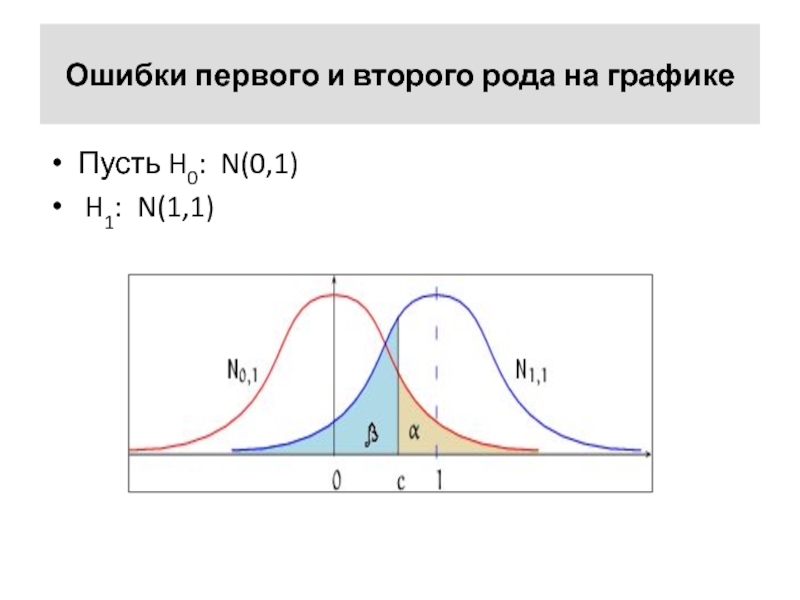
Слайд 25Ошибки первого и второго рода на графике
Пусть H0: N(0,1)
H1:
N(1,1)
Слайд 26Ошибка первого рода
Определение. Ошибка первого рода
состоит в том, что
H0 отвергается, когда она
верна.
Вероятность ошибки 1 –го рода обозначается
α,
α = P(T€ V/ H0) (значение статистики Т
принадлежит критической области V при
условии, что верна H0) .
α – это уровень значимости.
Слайд 27Ошибка второго рода
Определение. Ошибка второго рода
состоит в том, что
H0 не отвергается, когда она
не верна.
Вероятность ошибки 2
–го рода обозначается β.
β – это вероятность того, что значение
статистики Т не принадлежит критической
области V при условии, что верна H1.
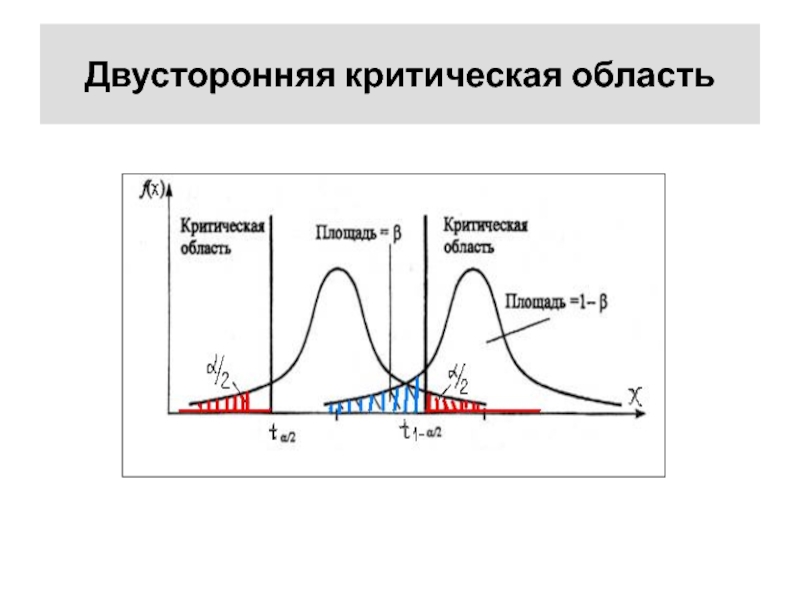
Слайд 29Двусторонняя критическая область
Слайд 30Мощность критерия
Определение. Мощностью критерия
называется величина М = 1
– β. Мощность
критерия М равна вероятности отвергнуть H0,
когда
она не верна.
М – это вероятность того, что значение
статистики Т принадлежит критической
области V при условии, что верна H1.
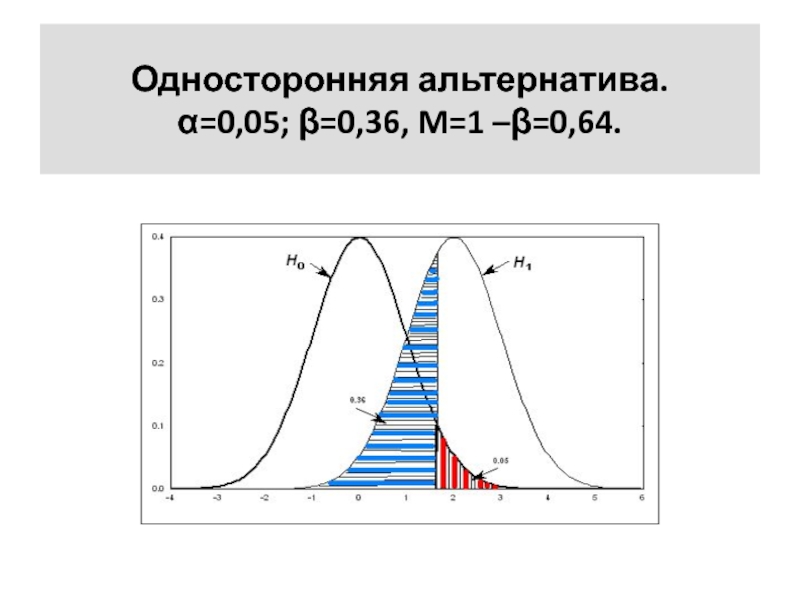
Слайд 31Односторонняя альтернатива.
α=0,05; β=0,36, M=1 –β=0,64.
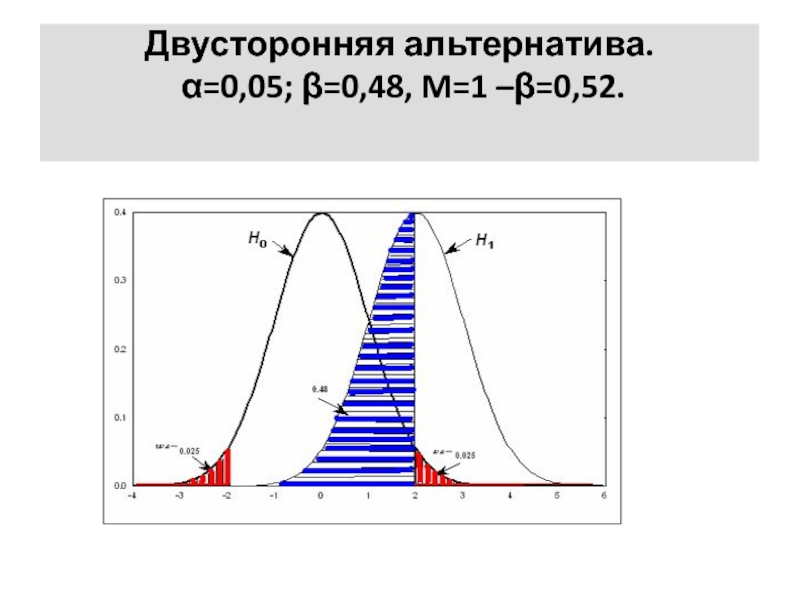
Слайд 32Двусторонняя альтернатива.
α=0,05; β=0,48, M=1 –β=0,52.
Слайд 33Замечание
Проверка статистических гипотез может проводиться методом доверительных интервалов.
Пример
H0: a
= 15; H1: a ≠ 15
α = 0,05
Доверительный интервал для a:
Ia = [12, 2; 14,8].
Значение a = 15 не входит в интервал Ia , следовательно,
H0 отвергается.