заданной вещественной частотой ωo.
Этот сигнал не является абсолютно интегрируемым, поскольку
при t ? +∞ функция s(t) не стремится ни к какому пределу. Преобразование Фурье S(ω) этого сигнала, рассматриваемое в обобщенном смысле, должно удовлетворять соотношению
Отсюда искомая спектральная плотность S(ω) выражается таким образом:
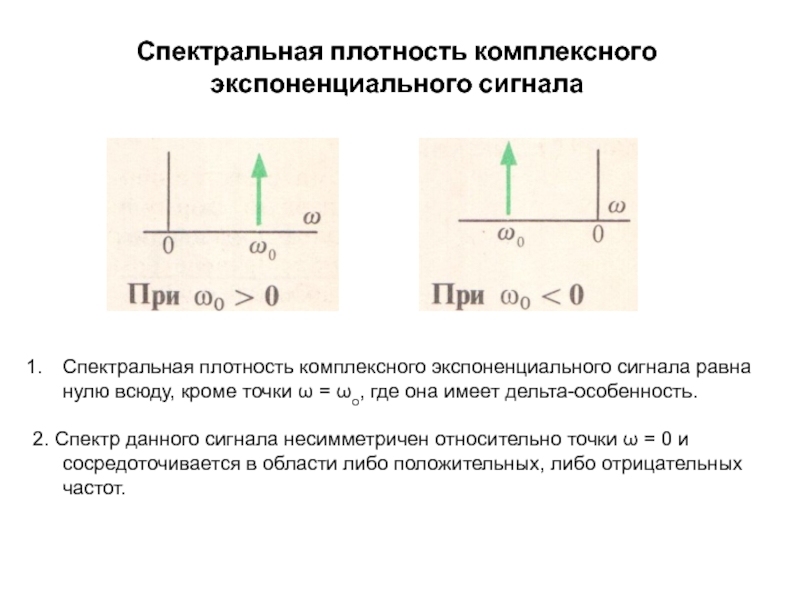
Спектральная плотность комплексного экспоненциального сигнала