Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема Понятие. Отношение. Логические операции
Содержание
- 1. Тема Понятие. Отношение. Логические операции
- 2. Понятие и его формы: суждения , умозаключения;Приёмы
- 3. Характеристика понятийПонятие - это форма мышления, отражающая
- 4. План лекции1. Приёмы образования понятий2. Содержание и
- 5. Приёмы образования понятийСоставить понятие о предмете означает
- 6. Сравнение - логический приём для установки сходства
- 7. Содержание и объём понятий
- 8. Слайд 8
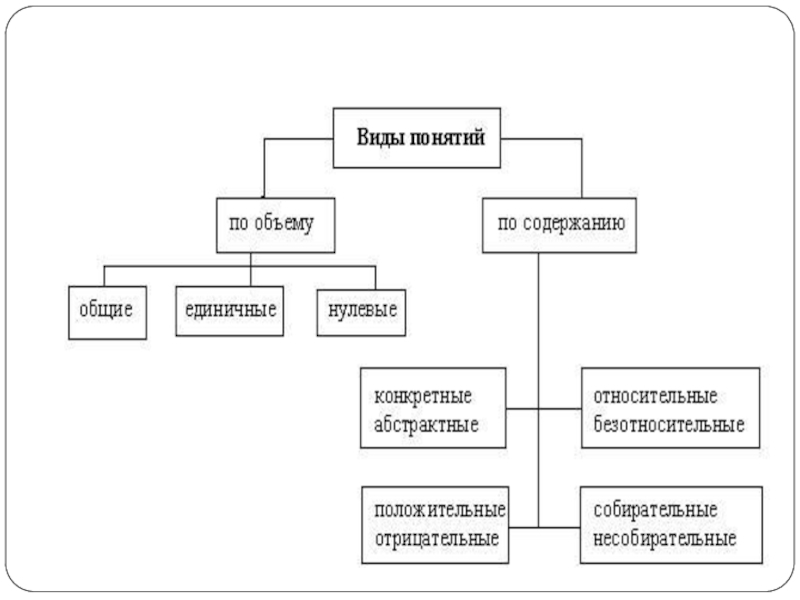
- 9. По объёму понятия бывают: ЕдиничнымиОбщимРегистрирующимиНерегистрирующимНулевыми(пустыми)
- 10. Единичными - понятия, которых составляет один единственный
- 11. По содержанию понятия бывают: КонкретныеАбстрактныеОтносительные БезотносительныеПоложительныеОтрицательныеСобирательныеНесобирательные
- 12. Конкретные - это понятия, в которых мыслится
- 13. Безотносительные - это такие понятия, в которых
- 14. Собирательными называются понятия, в которых группа однородных
- 15. Логические отношения между понятиямиТак как все предметы
- 16. Совместимые - это такие понятия, объемы которых
- 17. Слайд 17
- 18. Совместимые понятияПонятия находятся в отношении равнозначности (тождества)
- 19. Понятия находятся в отношении пересечения тогда, когда
- 20. Понятия находятся в отношении подчинения в том
- 21. Несовместимые понятияПонятия находятся в отношении соподчинения тогда,
- 22. Понятия находятся в отношении противоположности в том
- 23. Понятия находятся в отношении противоречия, если одно
- 24. Схематично можно изобразить не только отношения между
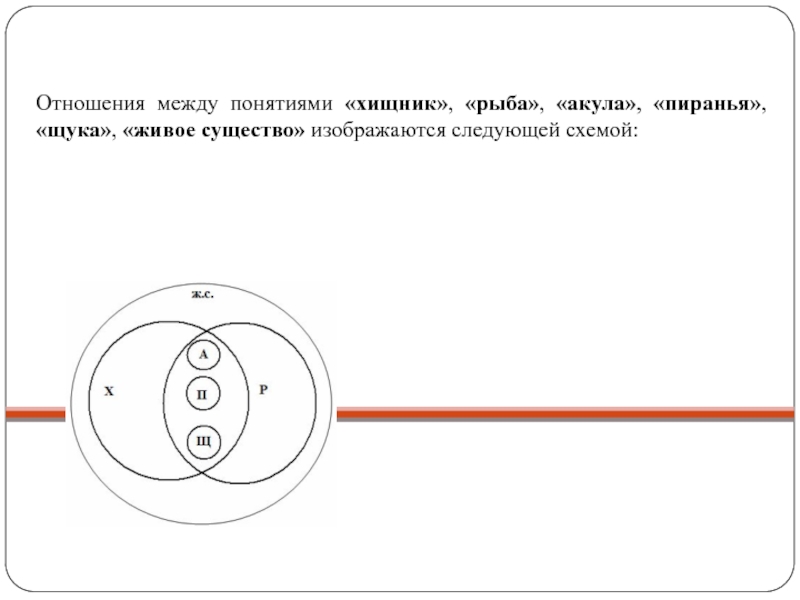
- 25. Отношения между понятиями «хищник», «рыба», «акула», «пиранья», «щука», «живое существо» изображаются следующей схемой:
- 26. Логические операции над понятиямиОбобщениеОграничениеОпределениеДеление
- 27. Ограничение и обобщение понятий Ограничение
- 28. Обобщение понятия — это логическая операция, которая противоположна
- 29. Ограничения и обобщения понятий складываются в логические
- 30. Пределом цепочки ограничения любого понятия всегда будет
- 31. Определение понятия Определение понятия — это логическая
- 32. Существует несколько логических правил определения. Нарушение хотя
- 33. Определение не должно быть узким, т.е. определение
- 34. Определение не должно быть широким и
- 35. 3. В определении не должно быть круга,
- 36. 4. Определение не должно быть двусмысленным, т.е.
- 37. 5. Определение не должно быть сложным и
- 38. Деление понятия Деление понятия - это логическая операция,
- 39. Существует несколько логических правил деления понятия. Нарушение
- 40. В делении с подменой основания могут использоваться
- 41. 3. Результаты деления не должны пересекаться, т.е.
- 42. Сложение и умножение понятийСложение понятий — это логическая
- 43. Умножение понятий — это логическая операция объединения двух
- 44. Скачать презентанцию
Понятие и его формы: суждения , умозаключения;Приёмы образования понятий: сравнение, анализ, синтез, абстрагирование, обобщение;Содержание понятия, объём понятия, виды понятий, логические отношения между понятиями, логические операции с понятиямиОсновные понятияПонятиеОтношениеЛогические операцииКлючевые слова
Слайды и текст этой презентации
Слайд 1Гадзаова С.В., ГрГУ им. Я. Купалы
Выполнила Цынкус Ю.А.
Тема
Понятие. Отношение.
Логические операции
Слайд 2Понятие и его формы: суждения , умозаключения;
Приёмы образования понятий: сравнение,
анализ,
синтез, абстрагирование, обобщение;
Содержание понятия, объём понятия, виды понятий,
логические
отношения между понятиями, логическиеоперации с понятиями
Основные понятия
Понятие
Отношение
Логические операции
Ключевые слова
Слайд 3Характеристика понятий
Понятие - это форма мышления, отражающая предметы в их
общих
признаках(свойств).
Отношение - математическая структура, которая формально определяет свойства различных объектов и
их взаимосвязи.Логическими операциями называют действия, вследствие которых порождаются новые понятия, возможно с использованием уже существующих.
Логические операции над понятиями — такие мыслительные действия, результатом которых является изменение содержания или объёма понятий, а также образование новых понятий.
Слайд 4План лекции
1. Приёмы образования понятий
2. Содержание и объём понятий
3. Виды
понятий
3. Логические отношения между понятиями
4. Логические операции над понятиями
Слайд 5Приёмы образования понятий
Составить понятие о предмете означает умение отличить его
среди других предметов, для этого логика использует операции:
сравнение
анализ
синтез абстрагирование
обобщение
Слайд 6Сравнение - логический приём для установки сходства и различия. Анализ -
мысленное расчленение на составные части. Синтез - соединение составных частей. Абстрагирование-отвлечение от
одних свойств с целью более детального изучения других. Обобщение - способ познания посредством определения общих существенных признаков объектов. Обобщение базируется на анализе и синтезе, направленных на установление существенных признаков объектов, а также на сравнении, которое позволяет определить общие существенные признаки.Слайд 7Содержание и объём понятий
Содержание понятия –
наиболее важный признак (свойство) объекта, который обозначается этим понятием.
Объём понятия - количество объектов, которое охвачено этим понятием. Таким образом, каждое понятие объединяет в себе
класс объектов - объем этого понятия - и характеристическое свойство, присущее всем объектам этого класса, и только им, - содержание этого понятия.
Например, понятие "треугольник" соединяет в себе класс всевозможных треугольников (объем этого понятия) и характеристическое свойство - наличие трех сторон, трех вершин, трех углов (содержание понятия).
Между объемом и содержанием понятия существует обратное отношение: чем больше содержание понятия, тем меньше его объем, и наоборот.
Слайд 10Единичными - понятия, которых составляет один единственный предмет. Общим - понятия,
объём которых составляет множество предметов. Регистрирующими - понятие, в которых множество
мыслимых в них предметов поддаётся учёту. Нерегистрирующими - понятия, в которых множество мыслимых в них предметов не поддаётся учёту. Нулевыми (пустыми) - понятия, объемы которых представляют собой классы реально не существующих предметов и существование которых в принципе невозможно: "вечный двигатель", "русалка", "леший" и др.). От нулевых следует отличать понятия, отражающие предметы, которые реально не существуют в настоящее время, но существовали в прошлом или существование которых возможно в будущем: "древнегреческий философ", "термоядерная электростанция". Такие понятия не являются нулевыми.Слайд 11По содержанию понятия бывают:
Конкретные
Абстрактные
Относительные
Безотносительные
Положительные
Отрицательные
Собирательные
Несобирательные
Слайд 12Конкретные - это понятия, в которых мыслится предмет или совокупность
предметов как нечто самостоятельно существующее: "академия", "студент", "романс", "дом", "поэма
А. Блока "Двенадцать" и др. Абстрактные - это понятия, в которых мыслится не сам предмет, а какой-либо из признаков предмета, взятый отдельно от самого предмета: "смелость", "добросовестность", "храбрость", "синева", "тождество" и др. Относительные - это такие понятия, в которых мыслятся предметы, существование одного из которых предполагает существование другого: " родители "-" дети "," учитель "- "ученик "," начальник "-" подчиненный "," истец "-" ответчик " и др.Слайд 13Безотносительные - это такие понятия, в которых мыслятся предметы, существующие
самостоятельно, вне зависимости от другого "фермер","правило","деревня","человек"и др. Положительные - это
понятия, содержание которых составляют свойства, присущие предмету: "принципиальность", "благородный поступок", "живущий по средствам", "успевающий студент" и др. Отрицательными называются понятия, в содержании которых указывается на отсутствие у предмета определенных свойств (например, "некрасивый поступок", "некрашеный дом", "некошеный луг" и др.). В русском языке отрицательные понятия выражаются обычно словами с отрицательными приставками "не" или "без" ("бес "): "неграмотный", "неверующий", "беззаконие", "беспорядок" и др. В словах иностранного происхождения - чаще всего словами с отрицательной приставкой "а": "агностицизм", "аморальный" и др.Слайд 14Собирательными называются понятия, в которых группа однородных предметов мыслится как
единое целое: "лес", "созвездие", "роща", "студенческий строительный отряд" и др.
Содержание собирательного понятия нельзя отнести к каждому отдельному элементу, входящему в объем этого понятия. Несобирательные - это такие понятия, содержание которых можно отнести к каждому предмету данного класса, который охватывается понятием: "дерево", "звезда", "студент" и др.Слайд 15Логические отношения между понятиями
Так как все предметы мира находятся во
взаимодействии и
взаимообусловленности, то и понятия, отражающие предметы мира,
такженаходятся в определенных отношениях.
Конкретные виды отношений устанавливаются в зависимости от
содержания и объема понятий, которые сравниваются.
Несравнимые понятия, если не имеют общих признаков, далеки
по содержанию.
Сравнимые понятия имеют общие признаки. Сравнимые понятия
делятся по объему на совместимые и несовместимые.
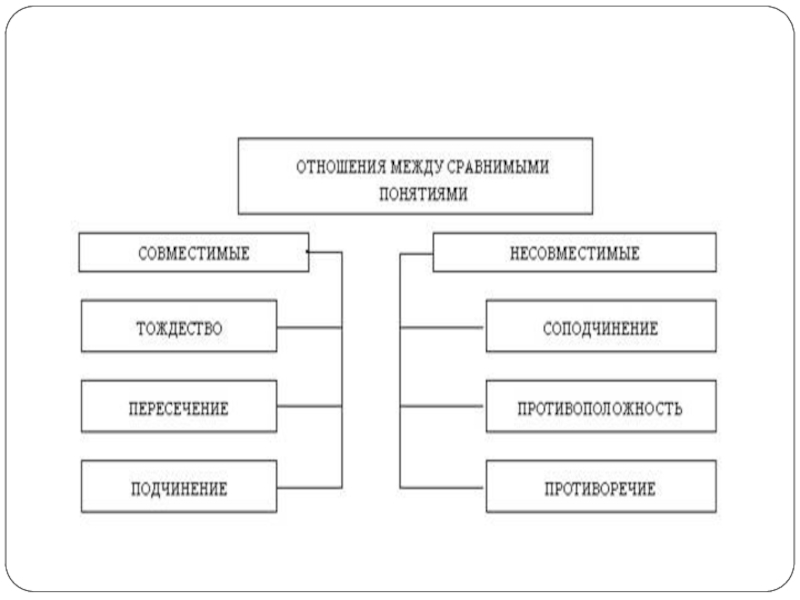
Слайд 16Совместимые - это такие понятия, объемы которых совпадают полностью или
частично. Несовместимые - это понятия, объемы которых не совпадают ни
в одном элементе. Отношения между понятиями принято иллюстрировать с помощью круговых схем (кругов Эйлера), где каждый круг обозначает объем понятия , а каждая точка - предмет, входящий в его объем. Круговые схемы позволяют наглядно представить отношения между различными понятиями, лучше понять и усвоить эти отношения.Слайд 18Совместимые понятия
Понятия находятся в отношении равнозначности (тождества) в том случае,
если их объемы полностью совпадают.
Так отношение равнозначности между понятиями «квадрат»
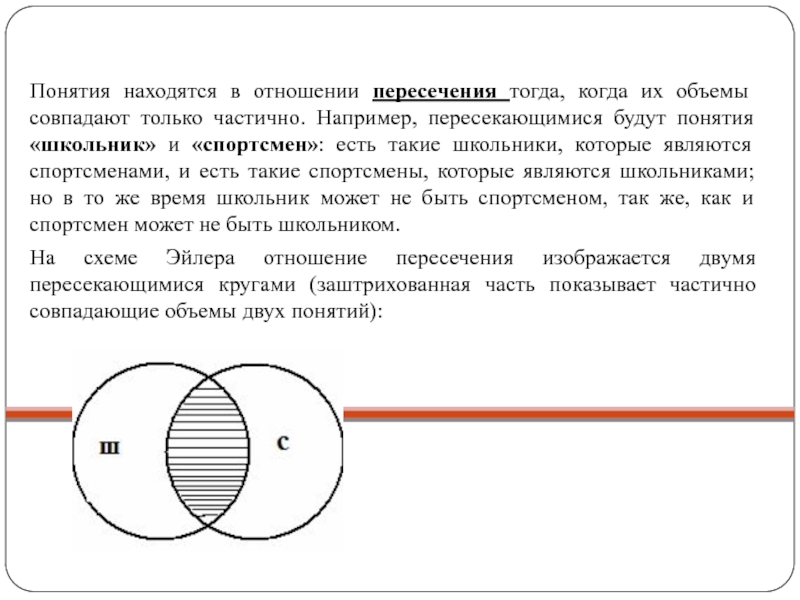
и «равносторонний прямоугольник» изображается схемой, на которой два круга, обозначающие два равных объема, полностью совпадают:Слайд 19Понятия находятся в отношении пересечения тогда, когда их объемы совпадают
только частично. Например, пересекающимися будут понятия «школьник» и «спортсмен»: есть
такие школьники, которые являются спортсменами, и есть такие спортсмены, которые являются школьниками; но в то же время школьник может не быть спортсменом, так же, как и спортсмен может не быть школьником.На схеме Эйлера отношение пересечения изображается двумя пересекающимися кругами (заштрихованная часть показывает частично совпадающие объемы двух понятий):
Слайд 20Понятия находятся в отношении подчинения в том случае, когда объем
одного из них обязательно больше объема другого и полностью его
в себя включает (один объем как бы подчиняется другому). Например, в отношении подчинения находятся понятия «карась» и «рыба», т.к. все караси — это обязательно рыбы, но рыбами.Рыбами являются не только караси, есть и другие виды рыб. Таким образом, объем понятия «карась» является меньшим по отношению к объему понятия «рыба» и полностью в него включается (подчиняется ему). В отношении подчинения понятия с меньшим объемом называются видовыми, а с большим — родовыми. На схеме Эйлера отношение подчинения изображается двумя кругами, один из которых располагается внутри другого
Слайд 21Несовместимые понятия
Понятия находятся в отношении соподчинения тогда, когда их объемы
не имеют общих элементов, но в то же время входят
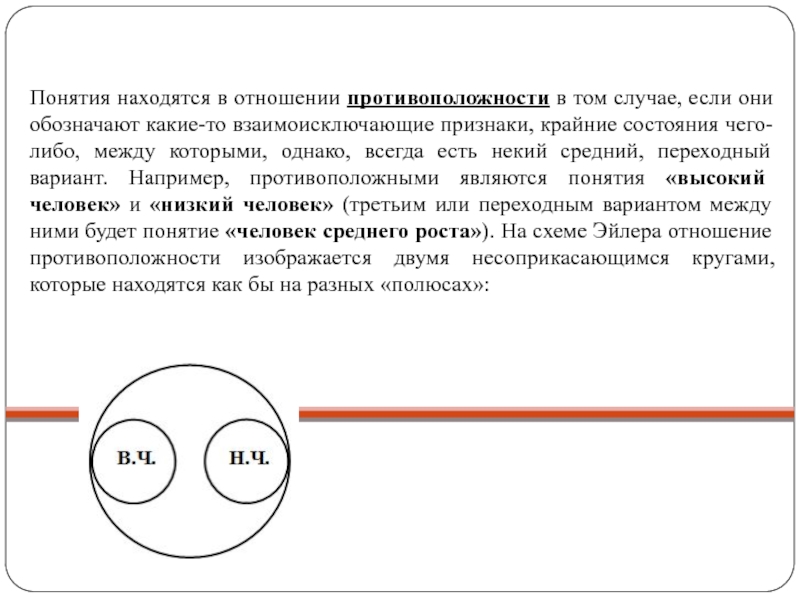
в объем какого-то третьего понятия, родового для них (совместно ему подчиняются). Например, понятия «сосна» и «береза» являются соподчиненными: ни одна сосна не может быть березой, и наоборот, но и множество всех сосен, и множество всех берез включается в более широкий объем понятия «дерево». На схеме Эйлера отношение соподчинения изображается двумя несоприкасающимися кругами:Слайд 22Понятия находятся в отношении противоположности в том случае, если они
обозначают какие-то взаимоисключающие признаки, крайние состояния чего-либо, между которыми, однако,
всегда есть некий средний, переходный вариант. Например, противоположными являются понятия «высокий человек» и «низкий человек» (третьим или переходным вариантом между ними будет понятие «человек среднего роста»). На схеме Эйлера отношение противоположности изображается двумя несоприкасающимся кругами, которые находятся как бы на разных «полюсах»:Слайд 23Понятия находятся в отношении противоречия, если одно из них представляет
собой отрицание другого, причем в отличие от противоположных понятий, между
противоречащими понятиями никак не может быть третьего или среднего варианта. Например, в отношении противоречия находятся понятия «высокий человек» и «невысокий человек». В том случае, когда одно понятие является отрицанием другого, третий вариант автоматически исключается: и «низкий человек», и «человек среднего роста» — это «невысокий человек». На схеме Эйлера отношение противоречия изображается одним кругом, поделенным на две части, которые обозначают противоречащие понятия:Слайд 24Схематично можно изобразить не только отношения между двумя понятиями, это
можно сделать и с большим количеством понятий. Например, отношения между
тремя понятиями «боксер», «негр» и «человек» . Взаимное расположение кругов показывает, что понятия «боксер» и «негр» находятся в отношении пересечения (боксер может быть негром и может им не быть, а также негр может быть боксером и может им не быть), а понятия «боксер» и «человек», так же как и понятия «негр» и «человек» находятся в отношении подчинения (любой боксер и любой негр — это обязательно человек, но человек может не быть ни боксером, ни негром).Слайд 25Отношения между понятиями «хищник», «рыба», «акула», «пиранья», «щука», «живое существо»
изображаются следующей схемой:
Слайд 27Ограничение и обобщение понятий
Ограничение понятия — это логическая операция
перехода от
родового понятия к видовому с помощью прибавления к
егосодержанию какого-либо признака. Вспомним об обратном отношении
между объемом и содержанием понятия: чем больше объем, тем
меньше содержание, и наоборот.
Ограничение понятия или переход от родового понятия к видовому — это уменьшение его объема, а значит — увеличение содержания. Вот почему при добавлении каких-то признаков к содержанию понятия автоматически уменьшается его объем. Например, если к содержанию понятия «ромб» прибавить признак «с прямым углом», то оно превратится в понятие «квадрат».