РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ 9

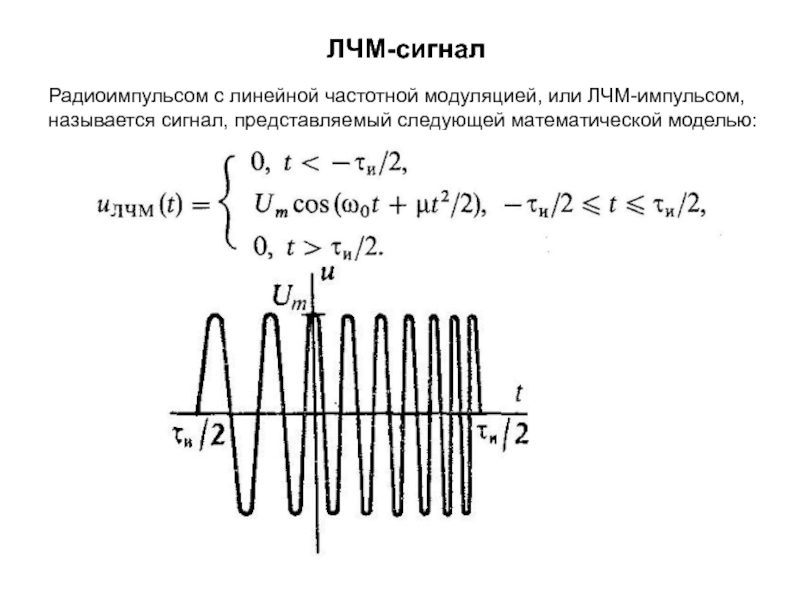
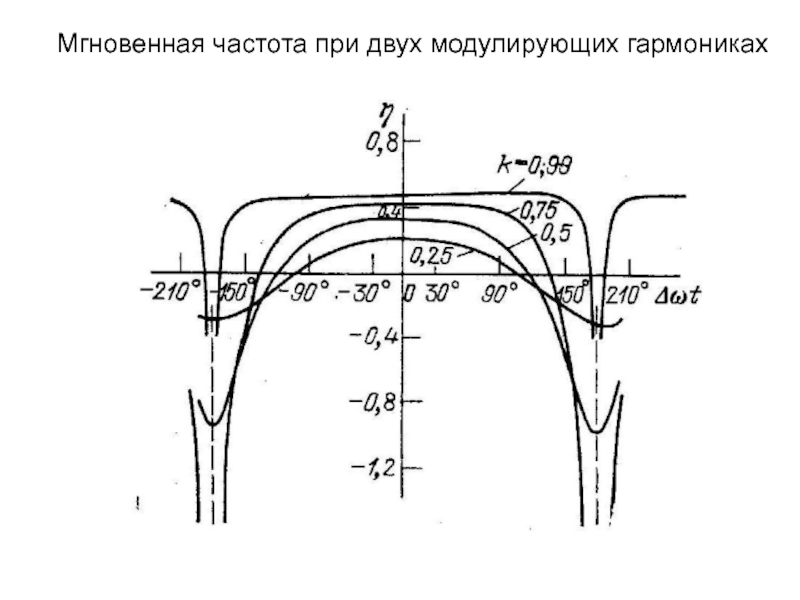
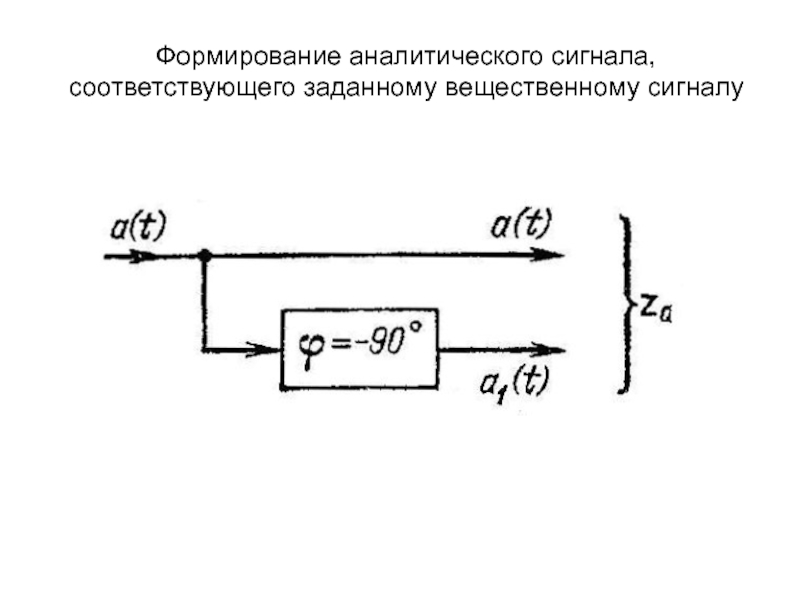
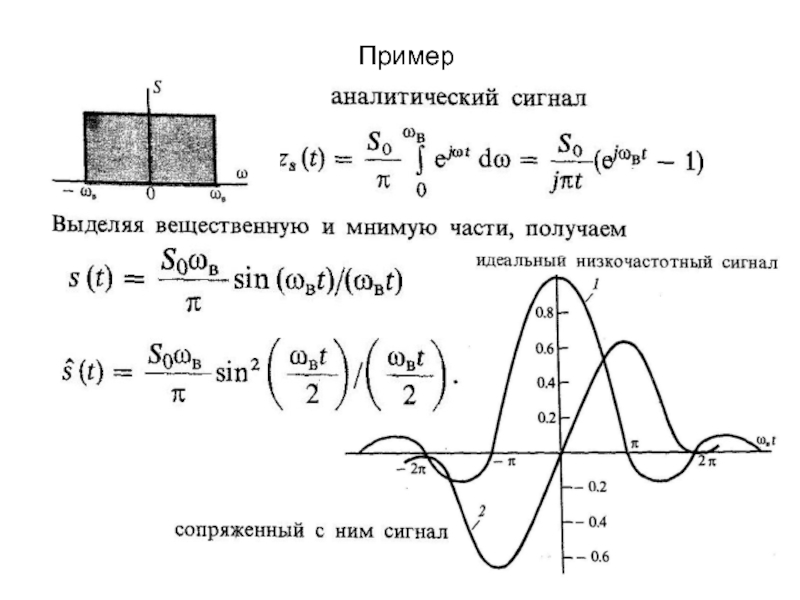
Будем полагать, что частота заполнения линейно нарастает от начала импульса

к его концу. Конкретизируя математическую модель сигнала, предположим, что его длительность равна причем точка t = 0 соответствует середине импульса, а мгновенная частота изменяется во времени по закону

Здесь — несущая частота; — параметр с размерностью с-2, равный скорости изменения частоты во времени.

За время, равное длительности импульса, девиация частоты

Полная фаза сигнала

следующей математической моделью:

практическую значимость, состоит в следующем.
Предположим,

что имеется некоторое физическое устройство, осуществляющее задержку сигналов, подаваемых на его вход. Если время задержки зависит от частоты сигнала, причем с ростом частоты это время уменьшается, то при определенных условиях, подавая на вход такого устройства ЛЧМ-импульс большой длительности, можно добиться существенного «сжатия» его во времени.
Этот эффект обусловлен тем, что на выходе устройства задержки одновременно будут появляться составляющие как более низкочастотные, относящиеся к началу импульса, так и более высокочастотные, наблюдаемые в его конце.

влияния отдельных спектральных составляющих.
На основании математической модели запишем выражение

спектральной плотности одиночного ЛЧМ-импульса:

плотности с резко выраженным максимумом в области положительных частот, близких

к Второй интеграл соответствует части спектральной плотности, сосредоточенной в основном при
На практике интересуются исключительно случаем, когда эффект перекрытия спектров, концентрирующихся при положительных и отрицательных частотах, пренебрежимо мал. Это связано с тем, что полная девиация частоты за время длительности импульса очень мала по сравнению с несущей частотой:

Поэтому в формуле следует вычислять только первый интеграл, дающий спектральную плотность при

Спектр в области отрицательных частот может быть получен на основании свойств преобразования Фурье для вещественных сигналов

квадрата, получим
Удобно перейти от переменной t к новому аргументу х,

выполнив замену переменной:

в выражении сводится к комбинации хорошо изученных специальных функций —

интегралов Френеля:

ЛЧМ-сигнала:
Представив эту спектральную плотность в показательной форме:
можно заметить, что модуль

(амплитудный спектр)

в то время как фазовый спектр состоит из квадратичного слагаемого

и остаточного члена

выражений свидетельствует о том, что характер частотной зависимости модуля и

фазы спектральной плотности прямоугольного ЛЧМ-импульса полностью зависит от безразмерного числа

равного произведению девиации частоты на длительность импульса и называемого базой ЛЧМ-сигнала.
В практически важных случаях выполняется условие
Спектр таких ЛЧМ-сигналов с большой базой имеет ряд особенностей. Во-первых, модуль спектральной плотности практически постоянен в пределах полосы частот шириной с центром в точке
Во-вторых, наблюдается постепенное исчезновение осцилляций модуля спектральной плотности с увеличением базы сигнала. Можно убедиться, что на центральной частоте спектра модуль спектральной плотности ЛЧМ-сигнала с большой базой

базы применяют по отношению к разнообразным сигналам. При этом

сигнал называют сложным при
, при 1 - простым.

Таким образом, модуль спектральной плотности ЛЧМ-сигнала с большой базой

Энергетический спектр такого сигнала

также постоянен в полосе частот
и обращается в нуль вне этой полосы.

= 10 ГГц и длительность

= 2 мкс. Девиация частоты за время импульса 0.1 ГГц.
Определить основные параметры спектра такого сигнала.

Прежде всего находим базу сигнала
В = 108*2*10-6 = 200.
Скорость нарастания частоты
*
Энергетический спектр

Поскольку база сигнала велика, его спектр практически заключен в пределах полосы частот
от 9.95 ГГц до = 10.05 ГГц.

при решении задач обнаружения сигнала, целесообразно использовать связь между АКФ

и энергетическим спектром сигнала, устанавливаемой парой интегральных преобразований Фурье.
Пусть база ЛЧМ-сигнала достаточно велика, так что энергетический спектр этого сигнала равномерен и сосредоточен лишь в полосе частот
вокруг несущей частоты. Тогда автокорреляционная функция ЛЧМ-сигнала:

Формула устанавливает следующее свойство ЛЧМ-сигнала: ширина главного лепестка огибающей АКФ обратно пропорциональна девиации частоты импульса.

нуль при сдвиге сигнала относительно его копии на интервал времени

Применяемые в радиолокации ЛЧМ-сигналы характеризуются значительной девиацией частоты, поэтому главный лепесток АКФ получается весьма узким.

Нормированная АКФ

Огибающая нормированной АКФ

нуль огибающей АКФ составит всего 0.01 мкс, или 0.5 %

от длительности импульса.
Однако с точки зрения корреляционных свойств ЛЧМ-сигналам присущ известный недостаток: высота двух первых симметричных боковых лепестков АКФ достаточно велика, составляя 0.212 от высоты центрального лепестка. В неблагоприятных условиях (значительный уровень шумов) это может привести к ошибочному определению временного положения импульса.

С точки зрения уровня боковых лепестков автокорреляционной функции ЛЧМ-сигнал существенно уступает сигналам Баркера при М = 13.

класс радиотехнических сигналов с ограниченным спектром, которые возникают на выходе

частотно-избирательных цепей и устройств.
По определению, сигнал называется узкополосным, если его спектральная плотность отлична от нуля лишь в пределах частотных интервалов шириной П, образующих окрестности точек
. причем должно выполняться условие

/ — низкочастотный сигнал, спектр которого сосредоточен в окрестности нулевой

частоты, то колебание при достаточно большом значении будет обладать всеми необходимыми признаками узкополосного сигнала, поскольку его спектр окажется сконцентрированным в малых окрестностях точек
Узкополосным будет и сигнал отличающийся фазой «быстрого» сомножителя. Наиболее общую математическую модель узкополосного сигнала можно получить, составив линейную комбинацию вида

Обе входящие сюда функции времени As(t) и Bs(t) являются низкочастотными в том смысле, что их относительные изменения за период высокочастотных колебаний достаточно малы. Функцию As(t) принято называть синфазной амплитудой узкополосного сигнала s(t) при заданном значении опорной частоты , а функцию Bs(t) — его квадратурной амплитудой.

квадратурную амплитуды можно выделить аппаратурным способом. Действительно, пусть имеется перемножающее

устройство, на один из входов которого подан узкополосный сигнал s(t), а на другой — вспомогательное колебание, изменяющееся во времени по закону . На выходе перемножителя будет получен сигнал

Пропустим выходной сигнал перемножителя через фильтр нижних частот (ФНЧ), подавляющий составляющие с частотами порядка
Ясно, что с выхода фильтра будет поступать низкочастотное колебание, пропорциональное синфазной амплитуде As(t).

называют комплексной амплитудой гармонического

колебания.
С физической точки зрения узкополосные сигналы представляют собой квазигармонические колебания.
Введем комплексную низкочастотную функцию

Комплексное представление узкополосных сигналов

В теории линейных электрических цепей широко применяется метод комплексных амплитуд, согласно которому гармоническое колебание выражается как вещественная или мнимая часть комплексных функций:

называемую комплексной огибающей узкополосного сигнала. Легко непосредственно проверить, что

узкополосному сигналу играет ту же роль, что и комплексная амплитуда

по отношению к простому гармоническому колебанию. Однако комплексная огибающая в общем случае зависит от времени - вектор Us(t) совершает на комплексной плоскости некоторое движение, изменяясь как по модулю, так и по направлению.

> 0 является гармоническим колебанием; в момент времени t =

0 частота сигнала изменяется скачком:

Взяв в качестве опорной частоты получим следующее выражение для комплексной огибающей данного сигнала:

Выбор опорной частоты обычно диктуется удобством расчета. Так, например, комплексная огибающая рассматриваемого сигнала относительно опорной частоты
имеет более сложный вид:

огибающую в показательной форме:.
Здесь Us(t) — вещественная неотрицательная функция времени,

называемая физической огибающей (часто, для краткости, просто огибающей), — медленно изменяющаяся во времени начальная фаза узкополосного сигнала.

Величины связаны с синфазной и квадратурной амплитудами соотношениями


откуда вытекает еще одна полезная форма записи математической модели узкополосного сигнала:

Us(t) через синфазную и квадратурную амплитуды:
2. Если вместо частоты

взять некоторую частоту то сигнал s(t) должен быть представлен в виде


и новое значение комплексной огибающей

Однако при этом физическая огибающая, являющаяся модулем комплексной огибающей, останется неизменной, поскольку выражение имеет единичный модуль.
3. Свойство физической огибающей состоит в том, что в каждый момент времени | s(t)| < Ua(t).

Важность понятия огибающей обусловлена тем, что в радиотехнике широко используются специальные устройства — амплитудные детекторы (демодуляторы), способность точно воспроизводить огибающую узкополосного сигнала.

спектральную
плотность, несимметричную относительно частоты

:

Спектральная плотность комплексной огибающей:

Используя обратное преобразование Фурье, находим комплексную огибающую

Несимметричная
плотность

Симметричная
плотность

вещественную и мнимую части:
Физическая огибающая рассматриваемого сигнала
Мгновенная частота :
имеет наибольшее

значение, равное в момент времени
t = 0.

Осциллограмма колебания s(t) представляет собой симметричный импульс
с непостоянной во времени частотой заполнения.