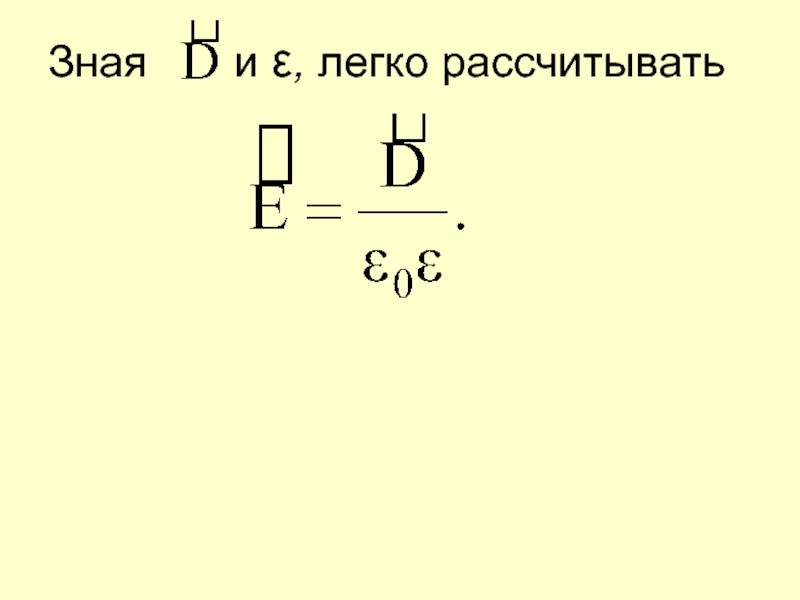Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расчет потенциалов простейших электростатических полей
Содержание
- 1. Расчет потенциалов простейших электростатических полей
- 2. Теорема Гаусса: иследовательно- оператор Лапласа (лапласиан) -
- 3. Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми заряженными телами
- 4. 6.2. Силовые линии и эквипотенциальные поверхностиНаправление силовой
- 5. Воображаемая поверхность, все точки которой имеют одинаковый
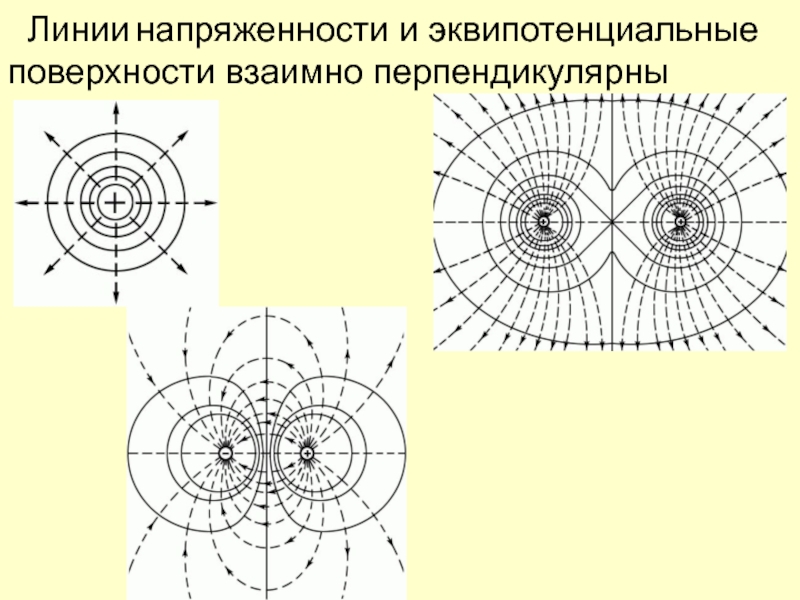
- 6. Линии напряженности и эквипотенциальные поверхности взаимно перпендикулярны
- 7. Формула выражает связь потенциала с напряженностью и
- 8. Интеграл можно брать по любой линии, соединяющие
- 9. Из обращения в нуль циркуляции вектора
- 10. 6.3. Расчет потенциалов простейшихэлектростатических полей6.3.1.Разность потенциалов между точками поля, образованного двумя бесконечными заряженными плоскостямиРис. 6.1,а
- 11. Мы показали, что напряженность связана с потенциалом
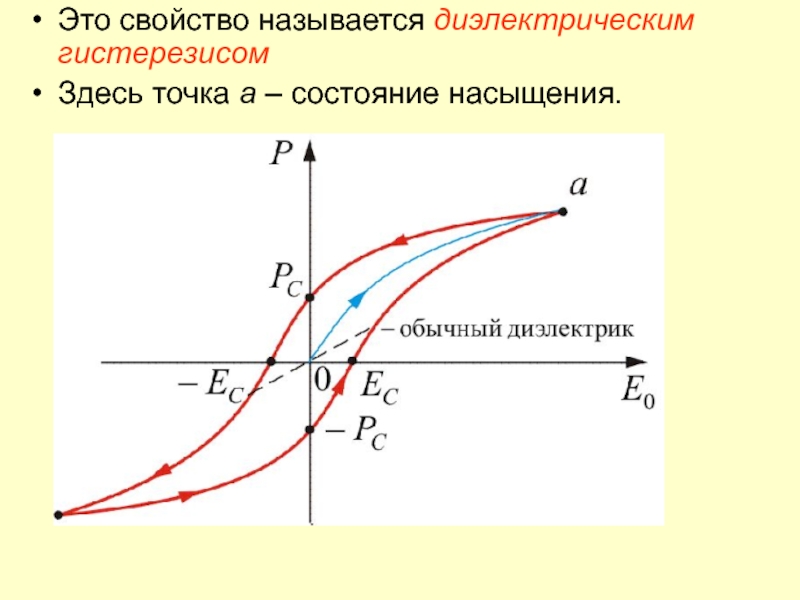
- 12. Чтобы получить выражение для потенциала между
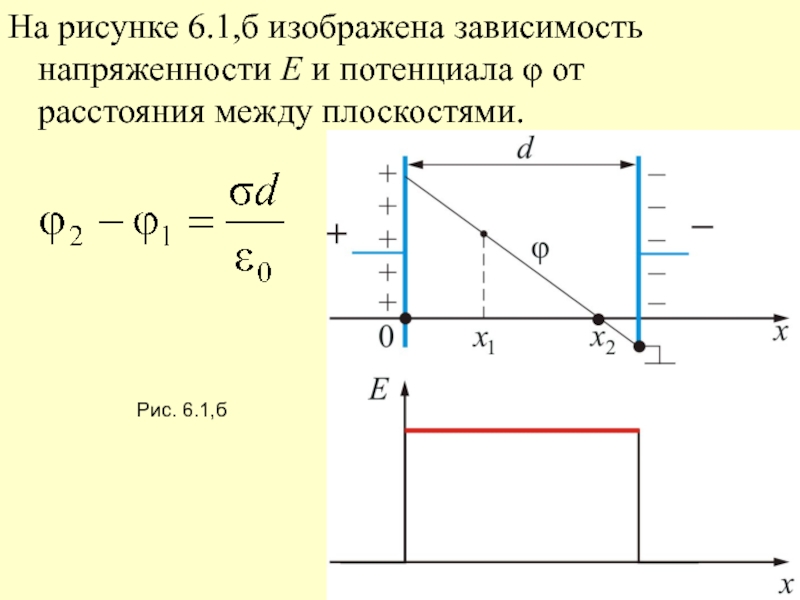
- 13. На рисунке 6.1,б изображена зависимость напряженности E и потенциала φ от расстояния между плоскостями.Рис. 6.1,б
- 14. 6. 3.2. Разность потенциалов между точками поля,
- 15. Тогда, т.к. отсюда следует, что разность
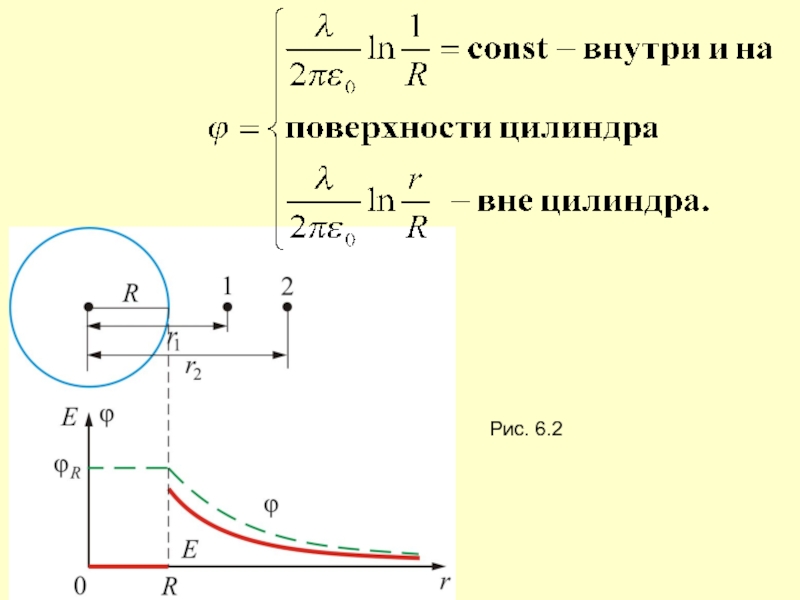
- 16. Рис. 6.2
- 17. 6.3.3. Разность потенциалов между обкладками
- 18. Т.к. , то
- 19. Таким образом, внутри меньшего цилиндра имеем, Е
- 20. 6. 3.4. Разность потенциалов между точками поля,
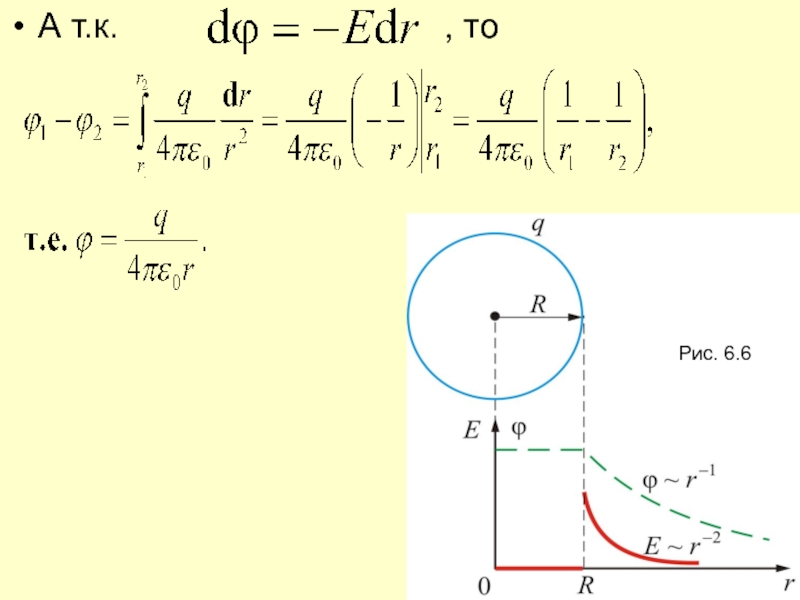
- 21. А т.к.
- 22. Из полученных соотношений можно сделать следующие выводы:С
- 23. 7.1. Поляризация диэлектриков;7.2. Различные виды диэлектриков:7.2.1. Сегнетоэлектрики;7.2.2.
- 24. До сих пор мы рассматривали электростатические поля
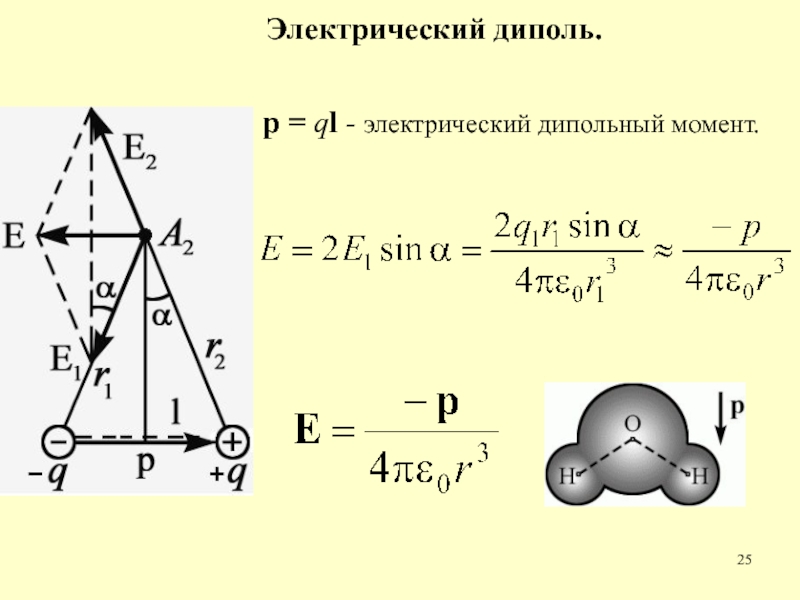
- 25. Электрический диполь.р = ql - электрический дипольный момент.
- 26. Диполь во внешнем поле Электрическое поле стремится
- 27. 4.1. Поляризация диэлектриков Все известные в природе
- 28. В идеальном диэлектрике свободных зарядов, то есть
- 29. Смещение электрических зарядов вещества под действием электрического
- 30. Поляризуемость диэлектрика включает составляющие – электронную, ионную и ориентационную (дипольную).
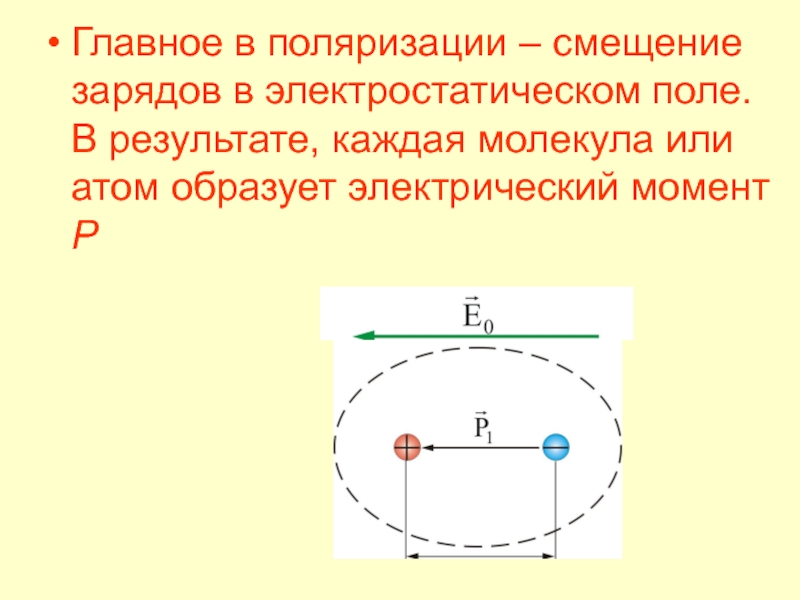
- 31. Главное в поляризации – смещение зарядов в
- 32. Внутри диэлектрика электрические заряды диполей компенсируют друг
- 33. Обозначим – электростатическое поле связанных
- 34. Поместим диэлектрик в виде параллелепипеда в электростатическое
- 35. Введем новое понятие – вектор поляризации –
- 36. С учетом этого обстоятельства,
- 37. Поверхностная плотность поляризационных зарядов равна нормальной составляющей
- 38. Вектор поляризации можно представить так:
- 39. Следовательно, и у результирующего поля изменяется, по
- 40. Величина
- 41. График зависимости напряженности электростатического поля шара от
- 42. 4.2. Различные виды диэлектриков В 1920 г.
- 43. Рассмотрим основные свойства сегнетоэлектриков:1. Диэлектрическая проницаемость ε
- 44. Это свойство называется диэлектрическим гистерезисом Здесь точка а – состояние насыщения.
- 45. 4. Наличие точки Кюри – температуры, при
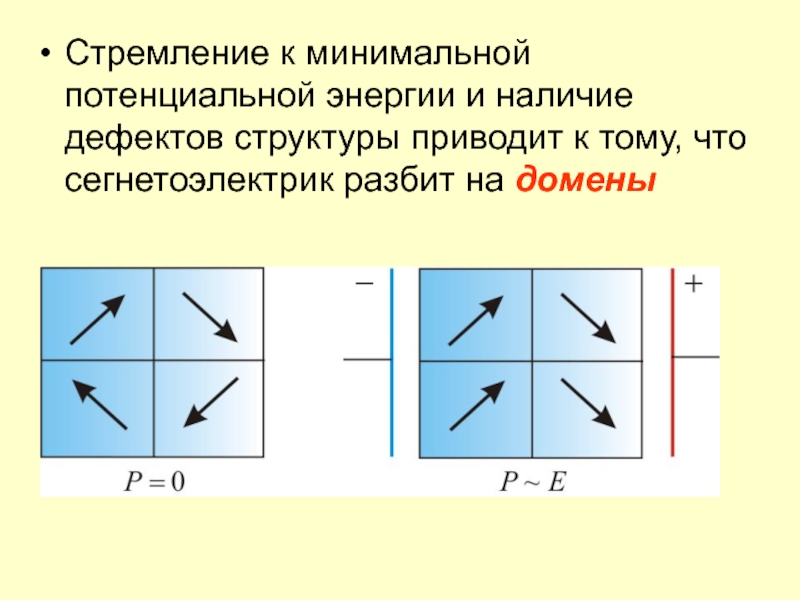
- 46. Стремление к минимальной потенциальной энергии и наличие
- 47. Среди диэлектриков есть вещества, называемые электреты –
- 48. ПьезоэлектрикиНекоторые диэлектрики поляризуются не только под
- 49. Рис.
- 50. Сейчас известно более 1800 пьезокристаллов. Все сегнетоэлектрики
- 51. 4.2.3. ПироэлектрикиПироэлектричество – появление электрических зарядов на
- 52. Все пироэлектрики являются пьезоэлектриками, но не наоборот. Некоторые пироэлектрики обладают сегнетоэлектрическими свойствами.
- 53. В качестве примеров использования различных диэлектриков можно
- 54. 4.3. Вектор электрического смещенияИмеем границу раздела двух
- 55. Главная задача электростатики – расчет электрических полей,
- 56. Для упрощения расчетов была введена новая векторная
- 57. Dn1 = Dn2.Таким образом, вектор
- 58. Зная и ε, легко рассчитывать
- 59. отсюда можно записать: (4.3.3)
- 60. Для точечного заряда в вакууме Для
- 61. 4.4. Поток вектора электрического смещения. Теорема Остроградского-Гаусса
- 62. В однородном электростатическом поле поток вектора равен:
- 63. Теорему Остроградского-Гаусса для вектора D получим из теоремы Остроградского-Гаусса для вектора E :
- 64. Теорема Остроградского-Гаусса для
- 65. 4.5. Изменение и
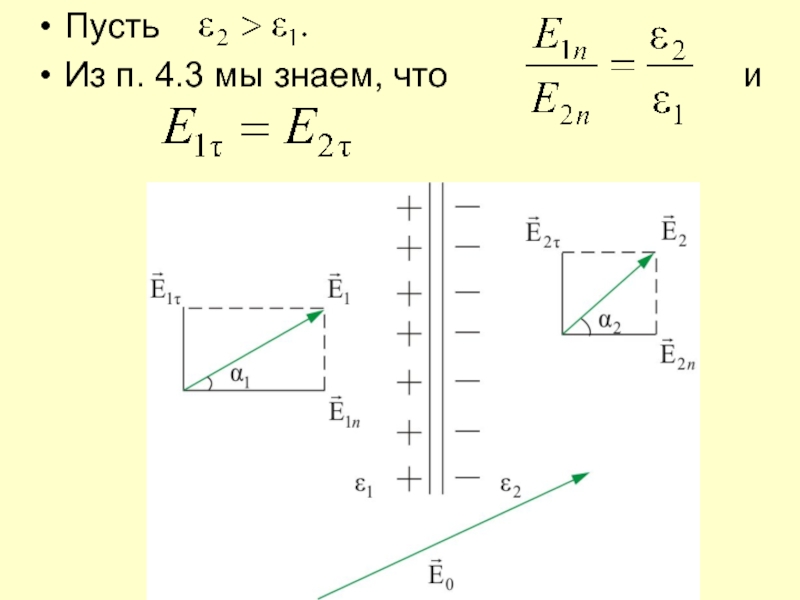
- 66. Пусть Из п. 4.3 мы знаем, что
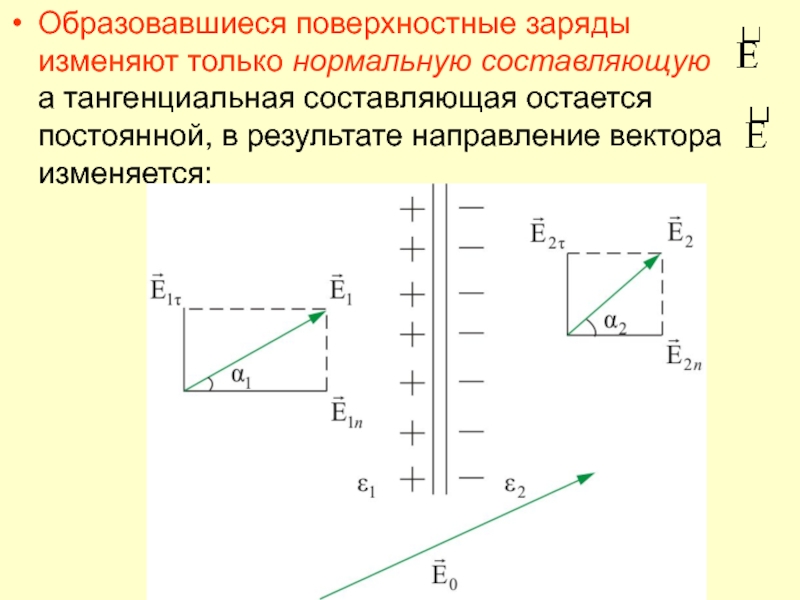
- 67. Образовавшиеся поверхностные заряды изменяют только нормальную составляющую
- 68. То есть направление вектора E изменяется: Это закон преломления вектора напряженности электростатического поля.
- 69. Рассмотрим изменение вектора D и его проекций и
- 70. Т.к.
- 71. закон преломления вектора D .
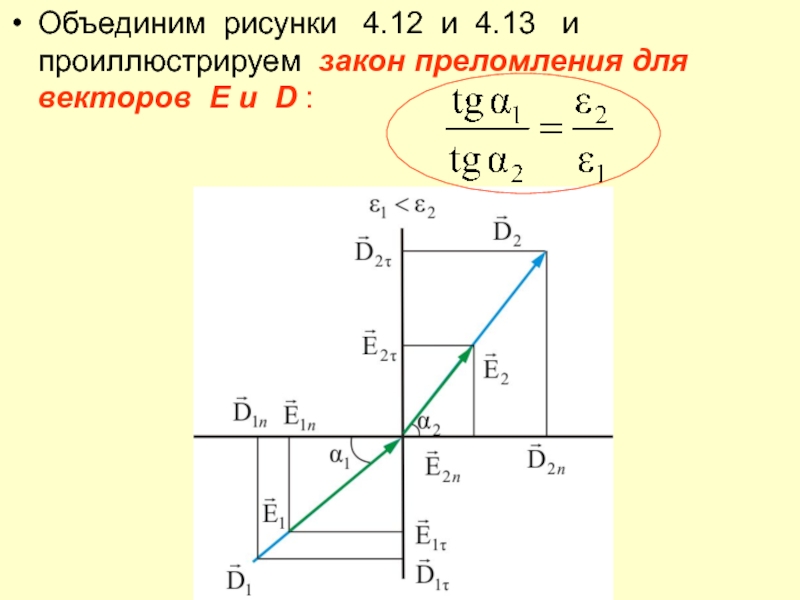
- 72. Объединим рисунки 4.12 и 4.13
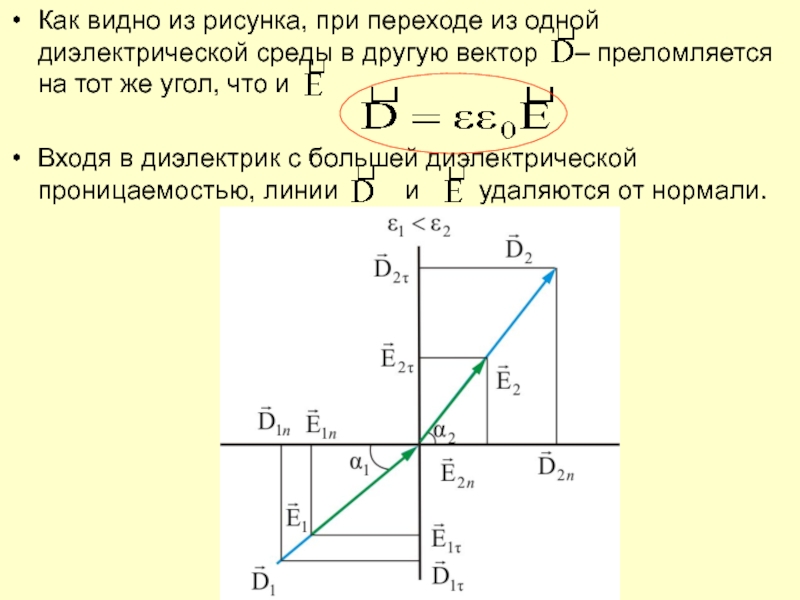
- 73. Как видно из рисунка, при переходе из
- 74. Лекция окончена.Сегодня: *
- 75. Лекция окончена.Сегодня: *
- 76. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 6. Расчет потенциалов простейших электростатических полей
6.1. Уравнения Лапласа и
Пуассона
Слайд 2
Теорема Гаусса:
и
следовательно
- оператор Лапласа (лапласиан)
- уравнение Пуассона
- уравнение
Лапласа
В области пространства, где заряды отсутствуют ρ=0
Слайд 3Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного
некоторыми заряженными телами
Слайд 46.2. Силовые линии и эквипотенциальные поверхности
Направление силовой линии (линии напряженности)
в каждой точке совпадает с направлением
.Отсюда следует, что напряженность равна разности потенциалов U на единицу длины силовой линии.
Именно вдоль силовой линии происходит максимальное изменение потенциала. Поэтому всегда можно определить
между двумя точками, измеряя U между ними, причем тем точнее, чем ближе точки.
В однородном электрическом поле силовые линии – прямые. Поэтому здесь определить наиболее просто:
(5.6.1)
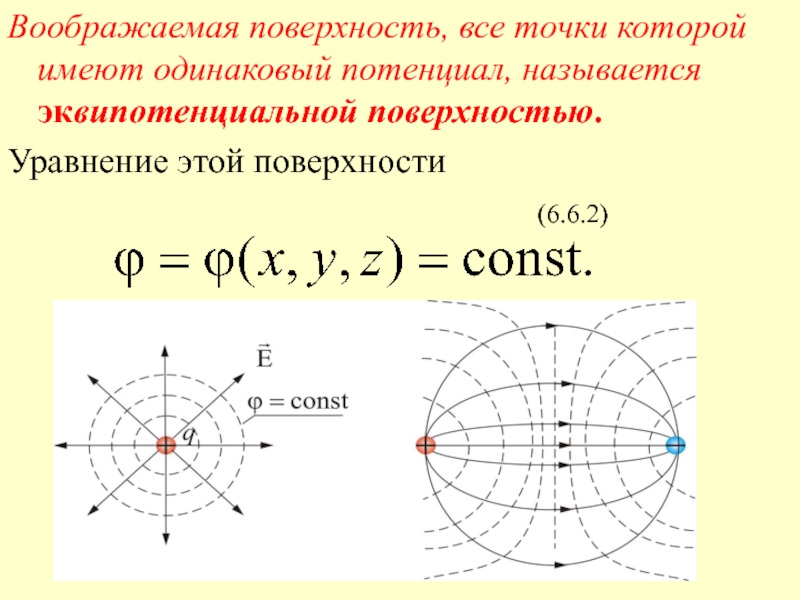
Слайд 5Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется
эквипотенциальной поверхностью.
Уравнение этой поверхности
(6.6.2)
Слайд 7Формула выражает связь потенциала с напряженностью и позволяет по известным
значениям φ найти напряженность поля в каждой точке.
Можно
решить и обратную задачу, т.е. по известным значениям в каждой точке поля найти разность потенциалов между двумя произвольными точками поля.
Слайд 8
Интеграл можно брать по любой линии, соединяющие точку 1 и
точку 2, ибо работа сил поля не зависит от пути.
Для обхода по замкнутому контуру получим:
т.е. пришли к известной нам теореме о циркуляции вектора напряженности: циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю.
Поле, обладающее этим свойством, называется потенциальным.
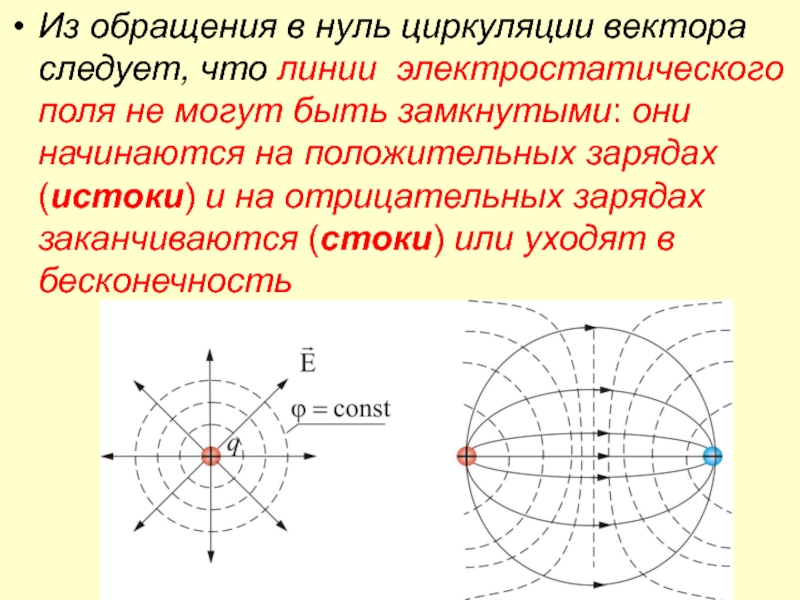
Слайд 9Из обращения в нуль циркуляции вектора следует, что линии
электростатического поля не могут быть замкнутыми: они начинаются на положительных
зарядах (истоки) и на отрицательных зарядах заканчиваются (стоки) или уходят в бесконечность
Слайд 106.3. Расчет потенциалов простейших
электростатических полей
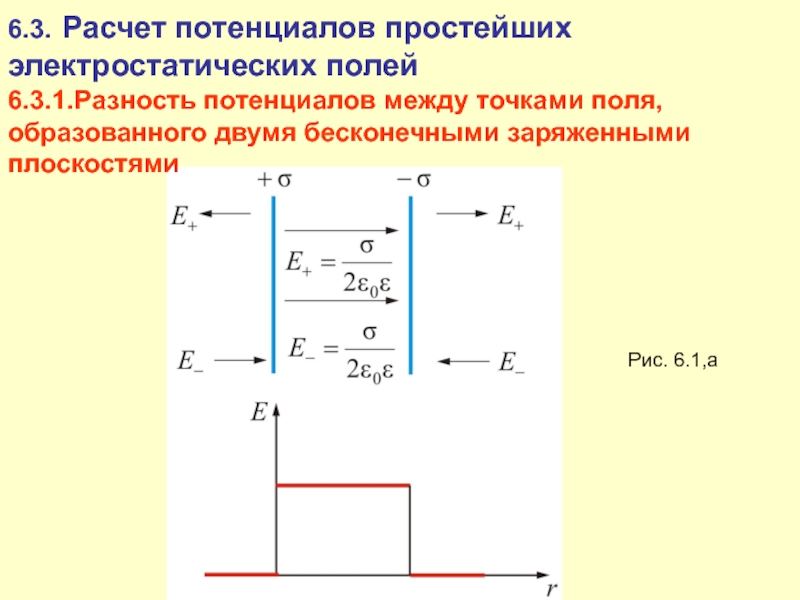
6.3.1.Разность потенциалов между точками поля, образованного
двумя бесконечными заряженными плоскостями
Рис. 6.1,а
Слайд 11Мы показали, что напряженность связана с потенциалом
тогда
(6.1.1)
где – напряженность
электростатического поля между заряженными плоскостями
σ = q/S – поверхностная плотность заряда.
Слайд 12 Чтобы получить выражение для потенциала между плоскостями, проинтегрируем выражение
При x1 = 0 и x2 = d (6.1.2)
Слайд 13На рисунке 6.1,б изображена зависимость напряженности E и потенциала φ
от расстояния между плоскостями.
Рис. 6.1,б
Слайд 146. 3.2. Разность потенциалов между точками поля, образованного бесконечно длинной
цилиндрической поверхностью
С помощью теоремы
Остроградского-Гаусса мы показали, что
Слайд 15Тогда, т.к.
отсюда следует, что разность потенциалов в произвольных
точках 1 и 2 будет равна:
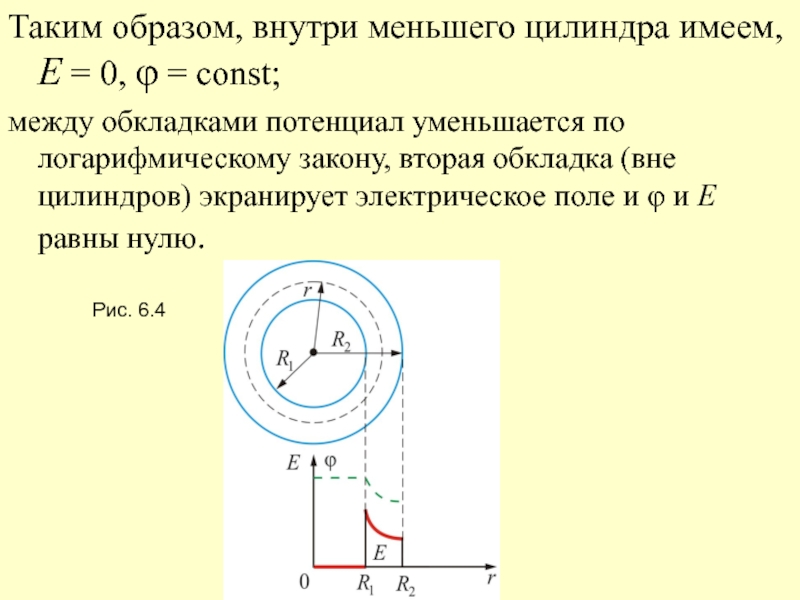
Слайд 19Таким образом, внутри меньшего цилиндра имеем, Е = 0, φ
= const;
между обкладками потенциал уменьшается по логарифмическому закону, вторая
обкладка (вне цилиндров) экранирует электрическое поле и φ и Е равны нулю.Рис. 6.4
Слайд 206. 3.4. Разность потенциалов между точками поля, образованного заряженной сферой
(пустотелой)
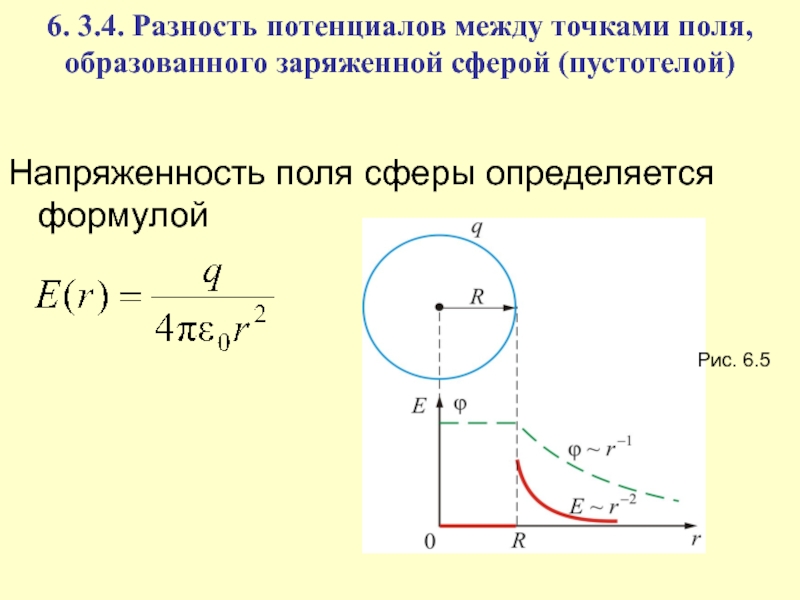
Напряженность поля сферы определяется формулой
Рис. 6.5
Слайд 22Из полученных соотношений можно сделать следующие выводы:
С помощью теоремы Гаусса
сравнительно просто можно рассчитать Е и φ от различных заряженных
поверхностей.Напряженность поля в вакууме изменяется скачком при переходе через заряженную поверхность.
Потенциал поля – всегда непрерывная функция координат.
Слайд 237.1. Поляризация диэлектриков;
7.2. Различные виды диэлектриков:
7.2.1. Сегнетоэлектрики;
7.2.2. Пьезоэлектрики;
7.2.3. Пироэлектрики;
7.3. Вектор
электрического смещения .
7.4. Поток вектора электрического смещения.
Теорема
Гаусса для вектора . 7.5. Изменение и на границе раздела
двух диэлектриков.
Лекция 7
Тема: ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
Сегодня: *
Слайд 24До сих пор мы рассматривали электростатические поля и взаимодействие зарядов
в вакууме. Как ведут себя заряды в среде? Что происходит
с веществом в электростатическом поле?Слайд 26Диполь во внешнем поле
Электрическое поле стремится повернуть ось диполя
так, чтобы его электрический момент р установился по направлению поля.
Положение равновесия, когда векторы p и E параллельны, устойчиво.Энергия диполя во
внешнем поле
Слайд 274.1. Поляризация диэлектриков
Все известные в природе вещества, в соответствии с
их способностью проводить электрический ток, делятся на
три основных класса:
диэлектрики
полупроводники
проводники
Слайд 28В идеальном диэлектрике свободных зарядов, то есть способных перемещаться на
значительные расстояния (превосходящие расстояния между атомами), нет.
Но это не
значит, что диэлектрик, помещенный в электростатическое поле, не реагирует на него, что в нем ничего не происходит.Слайд 29Смещение электрических зарядов вещества под действием электрического поля называется поляризацией.
Способность к поляризации является основным свойством диэлектриков.
Слайд 30Поляризуемость диэлектрика включает составляющие – электронную, ионную и ориентационную (дипольную).
Слайд 31Главное в поляризации – смещение зарядов в электростатическом поле. В
результате, каждая молекула или атом образует электрический момент Р
Слайд 32Внутри диэлектрика электрические заряды диполей компенсируют друг друга. Но на
внешних поверхностях диэлектрика, прилегающих к электродам, появляются заряды противоположного знака
(поверхностно связанные заряды).Слайд 33Обозначим – электростатическое поле связанных зарядов. Оно направлено
всегда против внешнего поля
Следовательно, результирующее электростатическое
поле внутри диэлектрика
Слайд 34Поместим диэлектрик в виде параллелепипеда в электростатическое поле
Электрический момент тела, можно найти по формуле:
– поверхностная плотность связанных зарядов.
Слайд 35Введем новое понятие – вектор поляризации – электрический момент единичного
объема.
(4.1.4)где n – концентрация молекул в единице объема,
– электрический момент одной молекулы.
Слайд 36С учетом этого обстоятельства,
(4.1.5)
(т.к. – объем параллелепипеда).
Приравняем (4.1.3.) и (4.1.5) и учтем, что – проекция P на направление – вектора нормали,
тогда
Слайд 37Поверхностная плотность поляризационных зарядов равна нормальной составляющей вектора поляризации в
данной точке поверхности.
Отсюда следует, что индуцированное в диэлектрике электростатическое поле
E' будет влиять только на нормальную составляющую вектора напряженности электростатического поля .
Слайд 38Вектор поляризации можно представить так:
(4.1.7)
где – поляризуемость молекул,
– диэлектрическая восприимчивость – макроскопическая безразмерная величина, характеризующая поляризацию единицы объема.
Слайд 39Следовательно, и у результирующего поля изменяется, по сравнению с
,только нормальная составляющая. Тангенциальная составляющая поля остается без
изменения.В векторной форме результирующее поле можно представить так:
(4.1.8)
Результирующая электростатического поля в диэлектрике равно внешнему полю, деленному на диэлектрическую проницаемость среды ε:
(4.1.9)
Слайд 40Величина
характеризует электрические свойства диэлектрика.
Физический смысл диэлектрической проницаемости среды
ε – величина, показывающая во сколько раз электростатическое поле внутри диэлектрика меньше, чем в вакууме:(4.1.10)
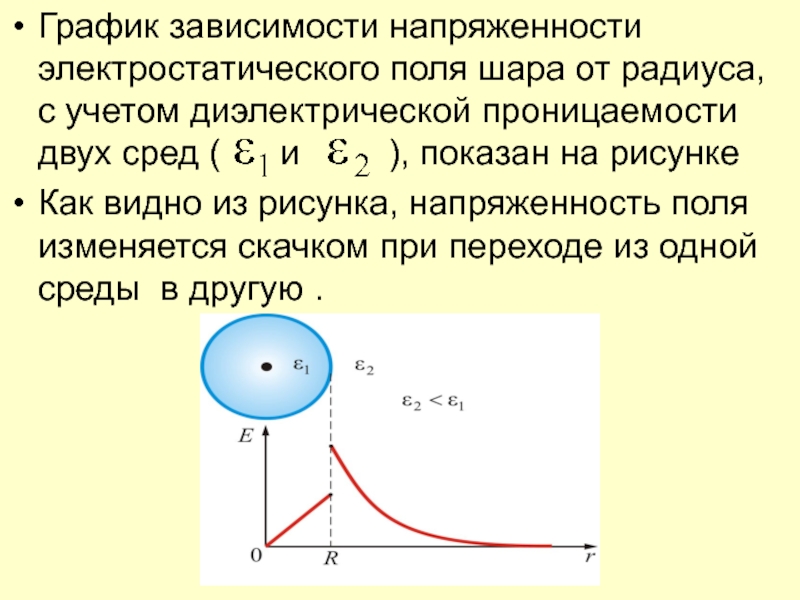
Слайд 41График зависимости напряженности электростатического поля шара от радиуса, с учетом
диэлектрической проницаемости двух сред ( и
), показан на рисункеКак видно из рисунка, напряженность поля изменяется скачком при переходе из одной среды в другую .
Слайд 424.2. Различные виды диэлектриков
В 1920 г. была открыта спонтанная (самопроизвольная)
поляризация.
Всю группу веществ, назвали сегнетоэлектрики (или ферроэлектрики).
Все сегнетоэлектрики обнаруживают резкую
анизотропию свойств (сегнетоэлектрические свойства могут наблюдаться только вдоль одной из осей кристалла). У изотропных диэлектриков поляризация всех молекул одинакова, у анизотропных – поляризация, и следовательно, вектор поляризации в разных направлениях разные.Слайд 43Рассмотрим основные свойства сегнетоэлектриков:
1. Диэлектрическая проницаемость ε в некотором температурном
интервале велика(
).2. Значение ε зависит не только от внешнего поля E0, но и от предыстории образца.
3. Диэлектрическая проницаемость ε (а следовательно, и Р ) – нелинейно зависит от напряженности внешнего электростатического поля (нелинейные диэлектрики).
Слайд 454. Наличие точки Кюри – температуры, при которой (и выше)
сегнетоэлектрические свойства пропадают. При этой температуре происходит фазовый переход 2-го
рода. Например,титанат бария: 133º С;
сегнетова соль: – 18 + 24º С;
ниобат лития 1210º С.
Слайд 46Стремление к минимальной потенциальной энергии и наличие дефектов структуры приводит
к тому, что сегнетоэлектрик разбит на домены
Слайд 47Среди диэлектриков есть вещества, называемые электреты – диэлектрики, длительно сохраняющие
поляризованное состояние после снятия внешнего электростатического поля (аналоги постоянных магнитов).
Слайд 48 Пьезоэлектрики
Некоторые диэлектрики поляризуются не только под действием электрического поля,
но и под действием механической деформации. Это явление называется пьезоэлектрическим
эффектом.Явление открыто братьями Пьером и Жаком Кюри в 1880 году.
Если на грани кристалла наложить металлические электроды (обкладки) то при деформации кристалла на обкладках возникнет разность потенциалов.
Если замкнуть обкладки, то потечет ток.
Слайд 49
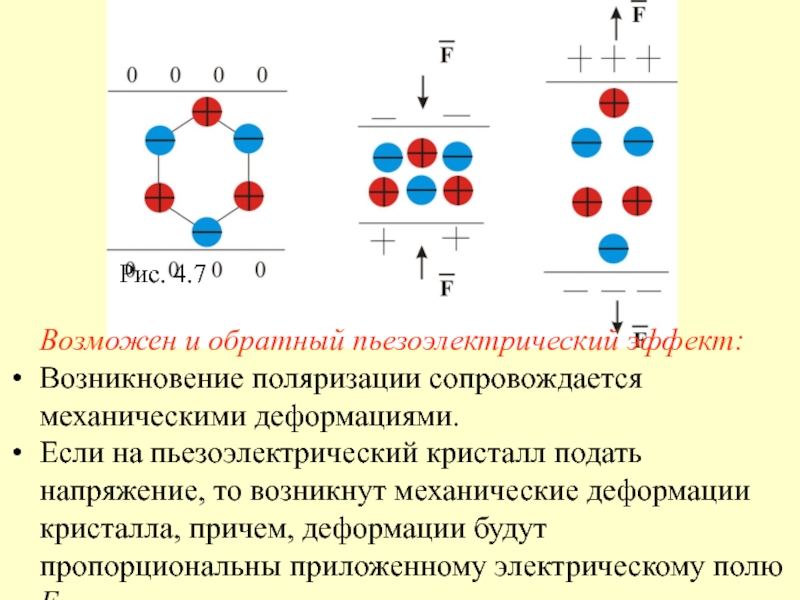
Рис. 4.7
Возможен и обратный
пьезоэлектрический эффект:
Возникновение поляризации сопровождается механическими деформациями.
Если на пьезоэлектрический кристалл
подать напряжение, то возникнут механические деформации кристалла, причем, деформации будут пропорциональны приложенному электрическому полю Е0.
Слайд 50Сейчас известно более 1800 пьезокристаллов.
Все сегнетоэлектрики обладают пьезоэлектрическими свойствами
Используются в пьезоэлектрических адаптерах и других устройствах).
Слайд 514.2.3. Пироэлектрики
Пироэлектричество – появление электрических зарядов на поверхности некоторых кристаллов
при их нагревании или охлаждении.
При нагревании один конец диэлектрика
заряжается положительно, а при охлаждении он же – отрицательно.Появление зарядов связано с изменением существующей поляризации при изменении температуры кристаллов.
Слайд 52Все пироэлектрики являются пьезоэлектриками, но не наоборот. Некоторые пироэлектрики обладают
сегнетоэлектрическими свойствами.
Слайд 53В качестве примеров использования различных диэлектриков можно привести:
сегнетоэлектрики – электрические
конденсаторы, ограничители предельно допустимого тока, позисторы, запоминающие устройства;
пьезоэлектрики – генераторы
ВЧ и пошаговые моторы, микрофоны, наушники, датчики давления, частотные фильтры, пьезоэлектрические адаптеры;пироэлектрики – позисторы, детекторы ИК-излучения, болометры (датчики инфракрасного излучения), электрооптические модуляторы.
Слайд 544.3. Вектор электрического смещения
Имеем границу раздела двух сред с ε1
и ε2, так что, ε1 < ε2 (рис. 4.8).
Рис.
4.8 или
Напряженность электрического поля E изменяется скачком при переходе из одной среды в другую.
Слайд 55Главная задача электростатики – расчет электрических полей, то есть
в различных электрических аппаратах, кабелях, конденсаторах,….
Эти
расчеты сами по себе не просты да еще наличие разного сорта диэлектриков и проводников еще более усложняют задачу.Слайд 56Для упрощения расчетов была введена новая векторная величина – вектор
электрического смещения (электрическая индукция).
(4.3.1)Из предыдущих рассуждений E1ε1 = ε2E2 тогда ε0ε1E1 = ε0ε2E2 отсюда и
Dn1 = Dn2.
Слайд 57Dn1 = Dn2.
Таким образом, вектор остается неизменным
при переходе из одной среды в другую и это облегчает
расчет .Слайд 59
отсюда можно записать:
(4.3.3)
– вектор поляризации,
χ – диэлектрическая восприимчивость среды,
характеризующая поляризацию единичного объема среды.где
Слайд 614.4. Поток вектора электрического смещения.
Теорема Остроградского-Гаусса для вектора
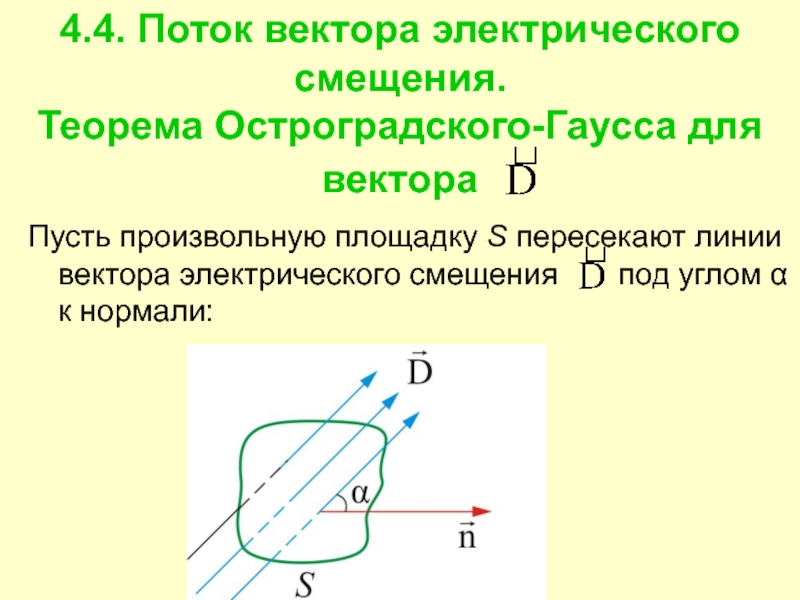
Пусть произвольную
площадку S пересекают линии вектора электрического смещения
под углом α к нормали:
Слайд 63Теорему Остроградского-Гаусса для вектора D получим из теоремы Остроградского-Гаусса для
вектора E :
Слайд 64Теорема Остроградского-Гаусса для
(4.4.1)
Поток вектора через любую замкнутую поверхность определяется только свободными зарядами, а не всеми зарядами внутри объема, ограниченного данной поверхностью.
Это позволяет не рассматривать связанные (поляризованные) заряды, влияющие на и упрощает решение многих задач.
В этом смысл введения вектора .
Слайд 654.5. Изменение и на границе раздела
двух диэлектриков
Рассмотрим простой случай (рисунок 4.12): два бесконечно протяженных диэлектрика
с ε1 и ε2, имеющих общую границу раздела, пронизывает внешнее электростатическое поле .
Слайд 67Образовавшиеся поверхностные заряды изменяют только нормальную составляющую
а тангенциальная составляющая остается постоянной, в результате направление вектора
изменяется:
Слайд 68То есть направление вектора E изменяется:
Это закон преломления вектора
напряженности электростатического поля.
Слайд 70Т.к.
, то имеем:
т.е. – нормальная составляющая вектора не изменяется.
т.е. тангенциальная составляющая вектора увеличивается в раз
Слайд 73Как видно из рисунка, при переходе из одной диэлектрической среды
в другую вектор – преломляется на тот же
угол, что иВходя в диэлектрик с большей диэлектрической проницаемостью, линии и удаляются от нормали.