Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Раздел 3. Прямые и плоскости в пространстве 3.1 Прямые в пространстве 3.1.1
Содержание
- 1. Раздел 3. Прямые и плоскости в пространстве 3.1 Прямые в пространстве 3.1.1
- 2. Стереометрия – раздел геометрии, в котором изучаются
- 3. Равными (конгруэнтными) фигурами называются такие две фигуры,
- 4. Слайд 4
- 5. Любая плоскость делит пространство на две области,
- 6. Аксиомы стериометрии:Аксиома 1: Через любые три точки
- 7. Аксиома 2: Если две плоскости имеют общую
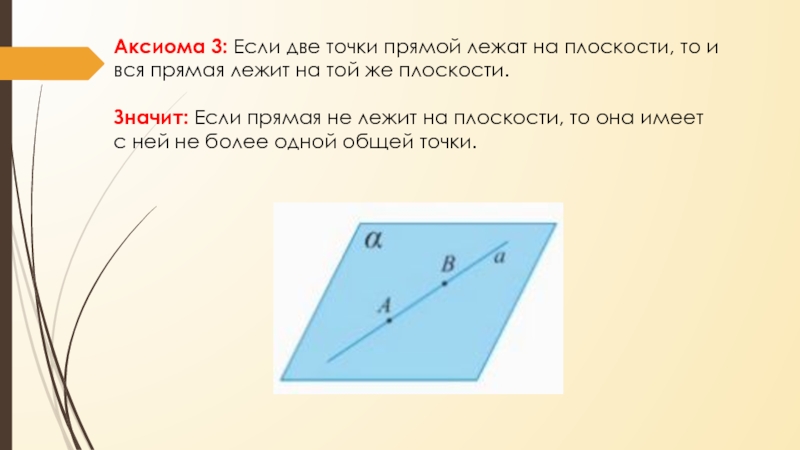
- 8. Аксиома 3: Если две точки прямой лежат
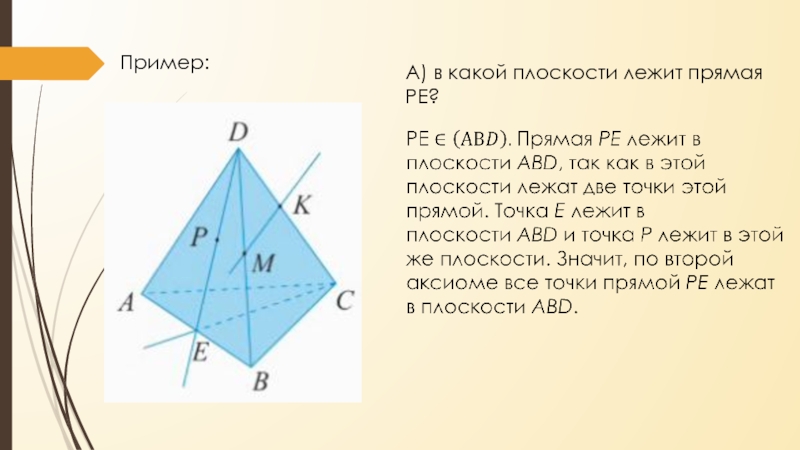
- 9. Пример:А) в какой плоскости лежит прямая РЕ?
- 10. Аксиома 4: Расстояние между любыми двумя точками
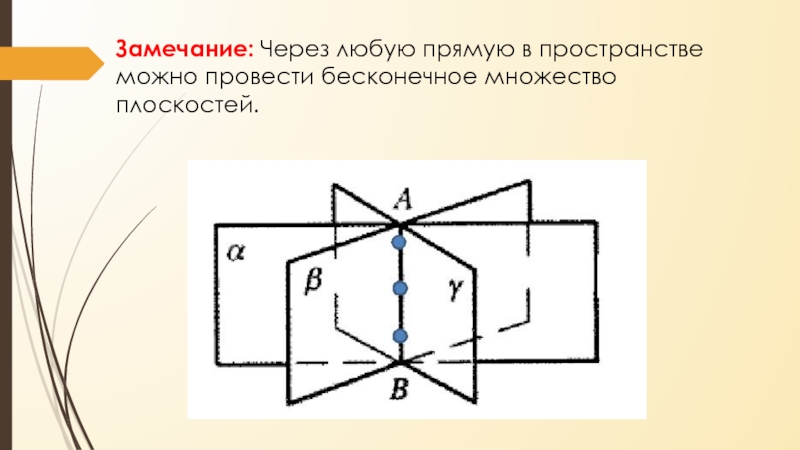
- 11. Замечание: Через любую прямую в пространстве можно провести бесконечное множество плоскостей.
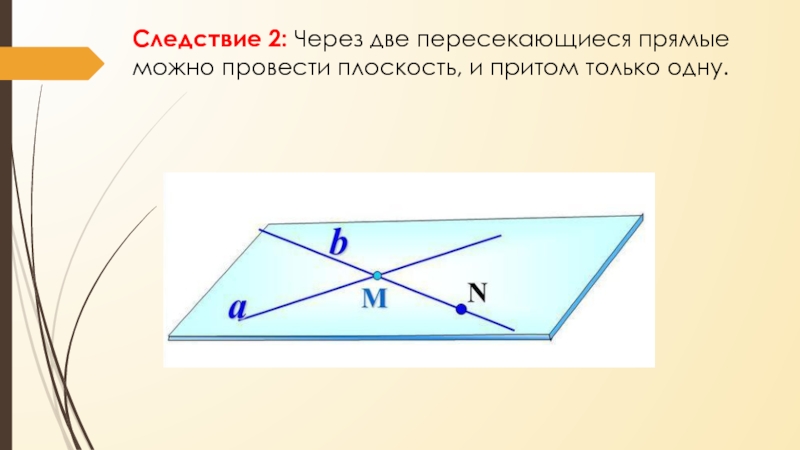
- 12. Следствие 2: Через две пересекающиеся прямые можно провести плоскость, и притом только одну.
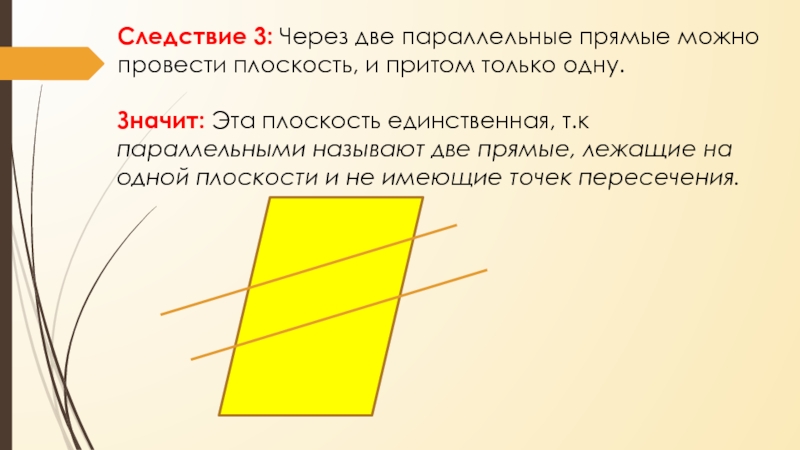
- 13. Следствие 3: Через две параллельные прямые можно
- 14. Аксиома (из планиметрии):Через точку, не лежащую на
- 15. В пространстве две прямые могут:Лежать на одной
- 16. Две прямые в пространстве, которые не имеют
- 17. Прямая и плоскость называются параллельными, если они
- 18. Замечания:Если плоскость проходит через данную прямую, параллельную
- 19. а) прямая лежит в плоскости; б) прямая
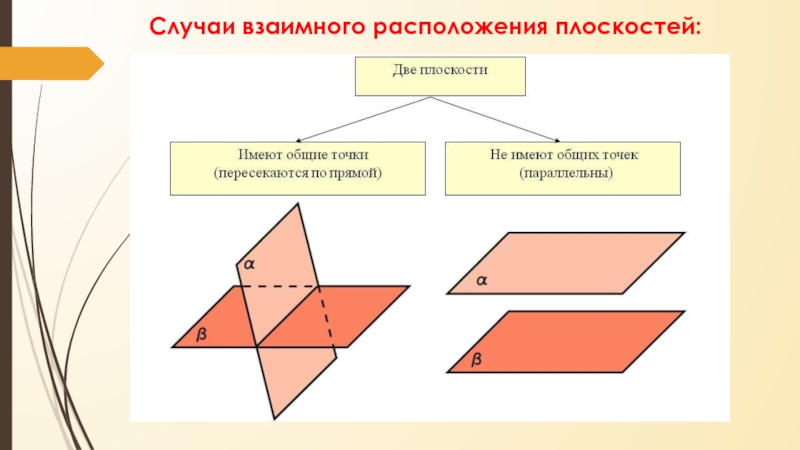
- 20. Случаи взаимного расположения плоскостей:
- 21. Свойства параллельных плоскостей:Если две параллельные плоскости пересечены
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Скачать презентанцию
Стереометрия – раздел геометрии, в котором изучаются фигуры в пространстве.Основные понятия стереометрии: точка, прямая, плоскость и расстояние от точки до точки. В стереометрии изучают свойства фигур, не все точки которых лежат
Слайды и текст этой презентации
Слайд 1Раздел 3. Прямые и плоскости в пространстве
3.1 Прямые в пространстве
3.1.1
Взаимное расположение двух прямых в пространстве.
Слайд 2Стереометрия – раздел геометрии, в котором изучаются фигуры в пространстве.
Основные
понятия стереометрии: точка, прямая, плоскость и расстояние от точки до
точки.В стереометрии изучают свойства фигур, не все точки которых лежат в одной плоскости – пространственных фигур.
Геометрическое тело – часть пространства, занимаемая предметом и изучаемая относительно её формы и размера, независимо от физических свойств предмета.
Геометрическое тело отделяется от окружающего пространства поверхностью.
Слайд 3Равными (конгруэнтными) фигурами называются такие две фигуры, которые можно совместить
так, чтобы они совпали во всех своих частях.
Две фигуры, состоящие
из одних и тех же точек, мы будем рассматривать как одну и ту же фигуру. Слайд 5Любая плоскость делит пространство на две области, расположенные по разные
стороны от этой плоскости
Если прямая имеет с плоскостью только одну
общую точку, то она ее пересекает, переходя из части пространства, лежащей по одну сторону плоскости, в часть пространства, лежащую по другую её сторону. Слайд 6Аксиомы стериометрии:
Аксиома 1: Через любые три точки пространства, не лежащие
на одной прямой, можно провести плоскость, при том только одну.
Слайд 7Аксиома 2: Если две плоскости имеют общую точку, то они
пересекаются по прямой, проходящей через эту точку.
Значит: Фигура, являющаяся прямой
в одной плоскости, является прямой и в любой другой плоскости, на которой она лежит. Поэтому, прямую в пространстве можно рассматривать саму по себе, независимо от плоскостей, в которых она лежит.Слайд 8Аксиома 3: Если две точки прямой лежат на плоскости, то
и вся прямая лежит на той же плоскости.
Значит: Если прямая
не лежит на плоскости, то она имеет с ней не более одной общей точки.Слайд 10Аксиома 4: Расстояние между любыми двумя точками пространства одно и
то же в любой плоскости, проходящей через эти точки.
Следствие 1:
Через прямую а и точку С вне ее можно провести плоскость, и при том только одну.Значит: На прямой а можно взять любые две точки, которые вместе с точкой С образуют три точки, не лежащие не на одной прямой => по А1 через эти три точки можно провести плоскость, и при том только одну.
Слайд 11Замечание: Через любую прямую в пространстве можно провести бесконечное множество
плоскостей.
Слайд 12Следствие 2: Через две пересекающиеся прямые можно провести плоскость, и
притом только одну.
Слайд 13Следствие 3: Через две параллельные прямые можно провести плоскость, и
притом только одну.
Значит: Эта плоскость единственная, т.к параллельными называют две
прямые, лежащие на одной плоскости и не имеющие точек пересечения. Слайд 14Аксиома (из планиметрии):
Через точку, не лежащую на заданной прямой, нельзя
провести более одной прямой, параллельной этой заданной прямой.
Она справедлива и
в стереометрии, тк если прямые в пространстве параллельны, то они лежат на одной плоскости. Слайд 15В пространстве две прямые могут:
Лежать на одной плоскости, при этом
:
- иметь общую точку (пересекающиеся прямые)
-
не иметь общих точек (параллельные прямые)Не лежать на одной плоскости и не иметь общих точек
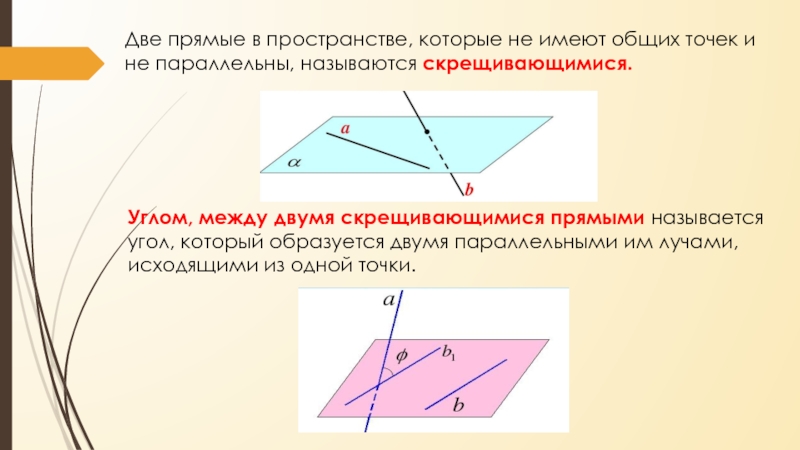
Слайд 16Две прямые в пространстве, которые не имеют общих точек и
не параллельны, называются скрещивающимися.
Углом, между двумя скрещивающимися прямыми называется угол,
который образуется двумя параллельными им лучами, исходящими из одной точки. Слайд 17Прямая и плоскость называются параллельными, если они не имеют общих
точек.
Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь
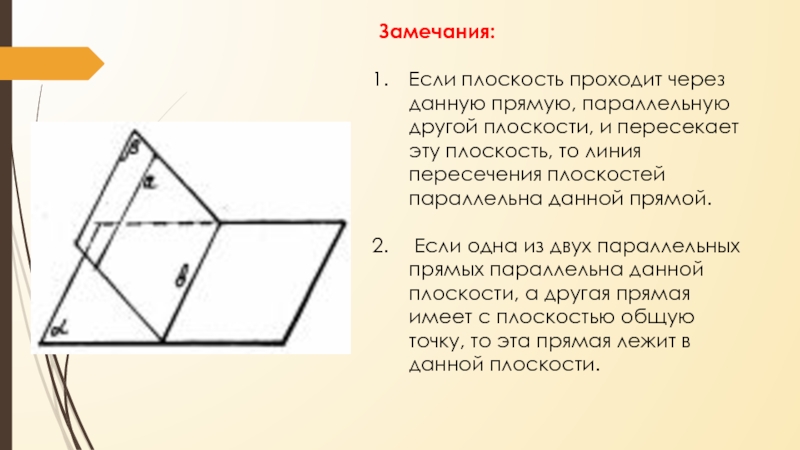
прямой, лежащей в этой плоскости, то она параллельна самой плоскости.Слайд 18Замечания:
Если плоскость проходит через данную прямую, параллельную другой плоскости, и
пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Если одна из двух параллельных прямых параллельна данной плоскости, а другая прямая имеет с плоскостью общую точку, то эта прямая лежит в данной плоскости.
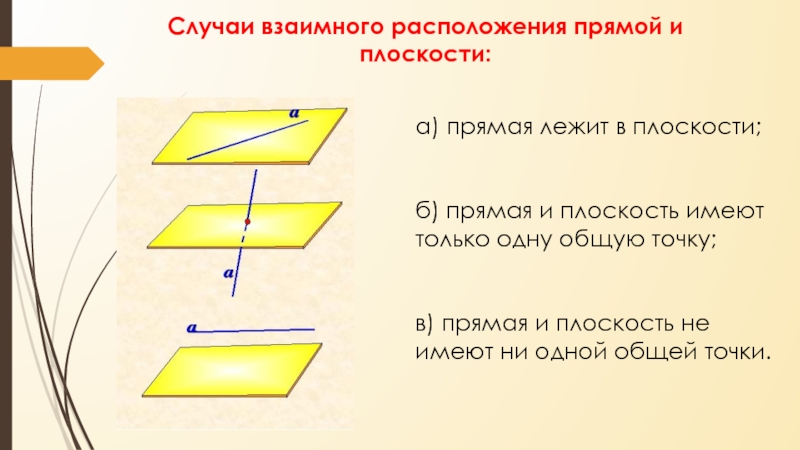
Слайд 19а) прямая лежит в плоскости;
б) прямая и плоскость имеют только
одну общую точку;
в) прямая и плоскость не имеют ни одной
общей точки.Случаи взаимного расположения прямой и плоскости: