Раздел № 2 Солодухин Е.А

Содержание

1. Раздел № 2 Солодухин Е.А
2. Прямая линия
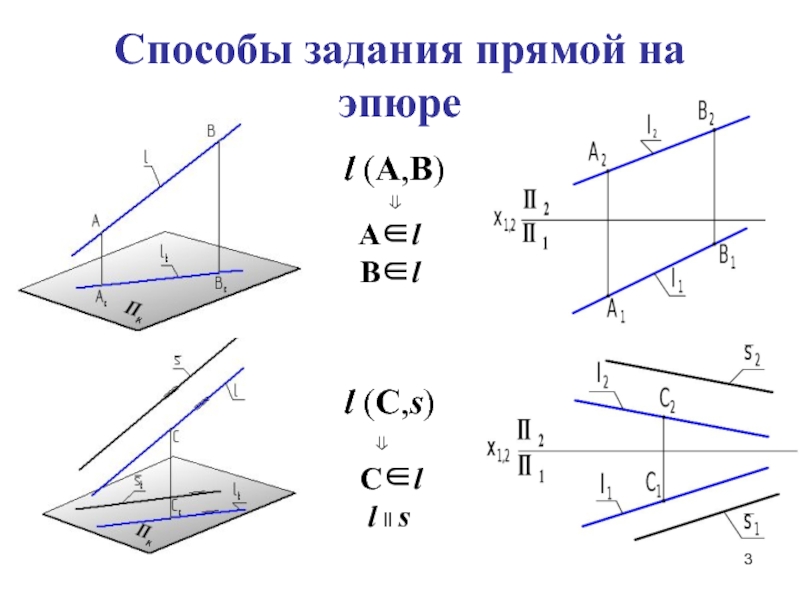
3. Способы задания прямой на эпюреl (A,B) Al Bll (С,s)  Cl l ll s
4. Положение прямой относительно плоскости проекцийПрямая общего
5. Слайд 5
6. Прямая общего положения Это прямая не параллельная и
7. l II П1 и l II П2l
8. Характерная особенность эпюра прямой общего положения –
9. Прямые частного положенияЭто прямые параллельные или перпендикулярные
10. Прямая уровняЭто прямая параллельная какой-либо одной плоскости проекцийl II Пк
11. ГоризонтальЭто прямая параллельная горизонтальной плоскости проекцийl II П1  l  h
12. Горизонталь - h
13. ФронтальЭто прямая параллельная фронтальной плоскости проекцийl II П2  l  f
14. Фронталь - f
15. Характерная особенность эпюра горизонтали и фронтали –
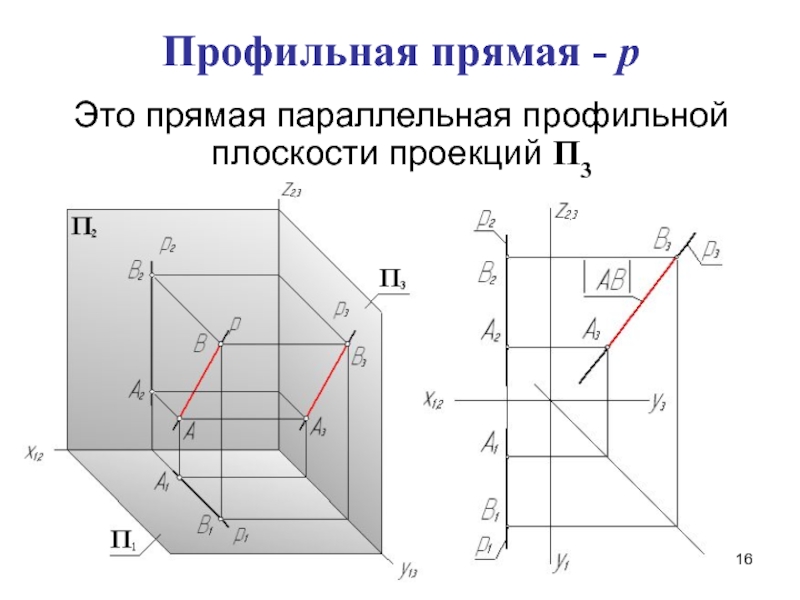
16. Профильная прямая - pЭто прямая параллельная профильной плоскости проекций П3
17. Проецирующая прямая Прямая перпендикулярная одной из плоскостей проекцийm  Пк
18. Горизонтально-проецирующая прямаяЭто прямая перпендикулярная горизонтальной плоскости проекцийm  П1
19. Горизонтально-проецирующая прямаяm  П1  m II
20. Фронтально-проецирующая прямаяЭто прямая перпендикулярная фронтальной плоскости проекцийm  П2
21. Фронтально-проецирующая прямаяm  П2  m II
22. Характерная особенность эпюра проецирующей прямой – одна из проекций прямой точка
23. Взаимное положение двух прямых
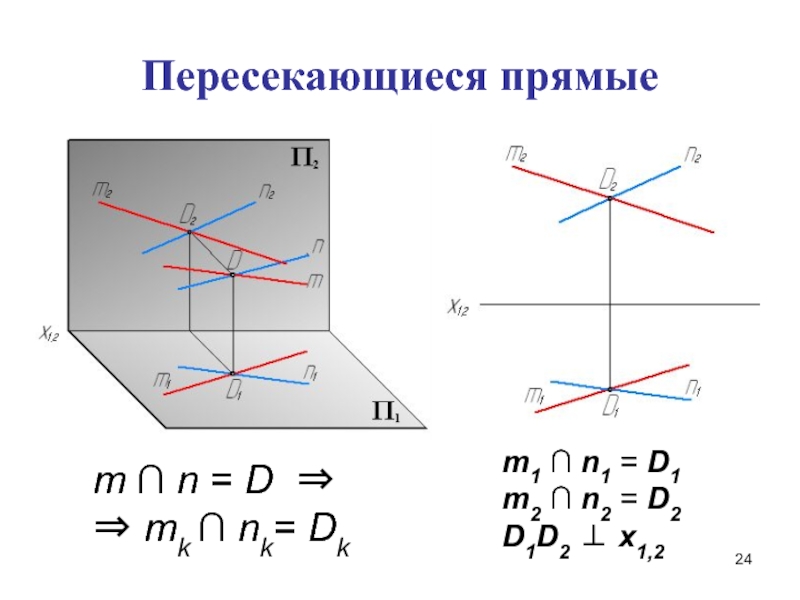
24. Пересекающиеся прямыеm ∩ n = D 
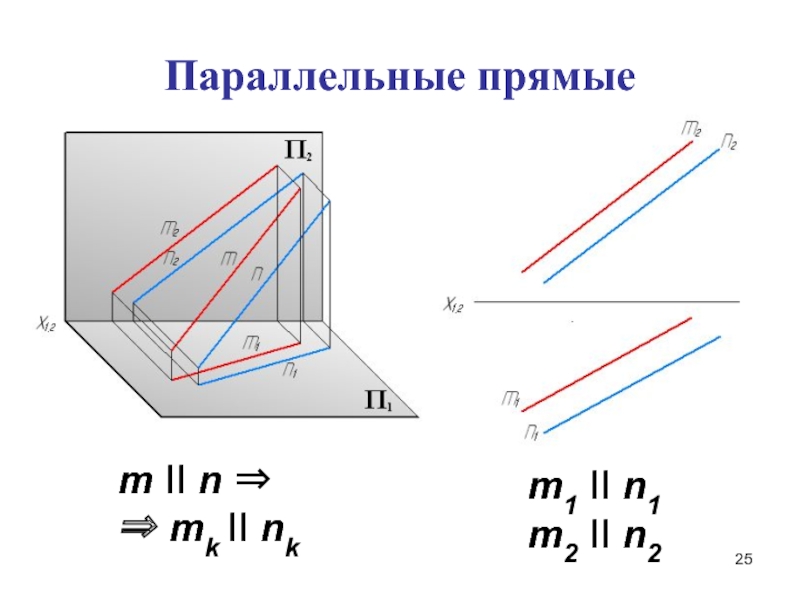
25. Параллельные прямыеm II n  mk II nkm1 II n1m2 II n2
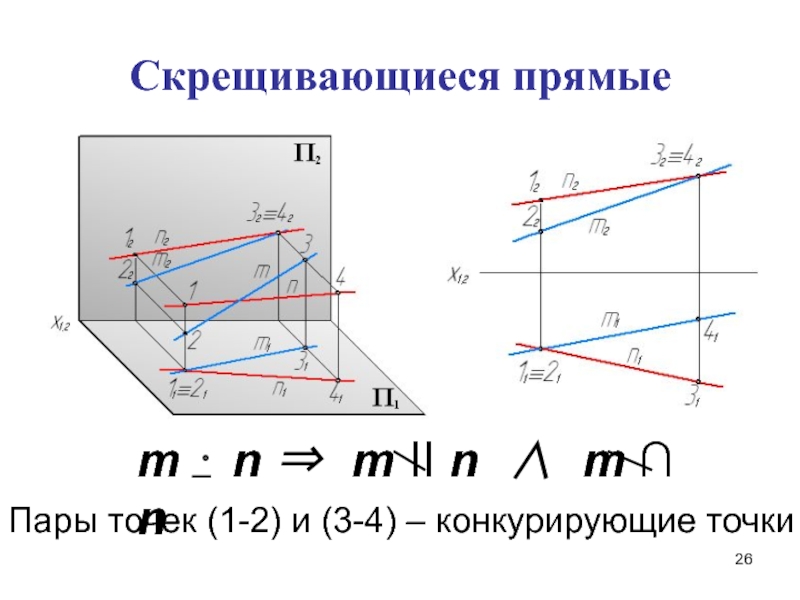
26. Скрещивающиеся прямыеm  n  m II
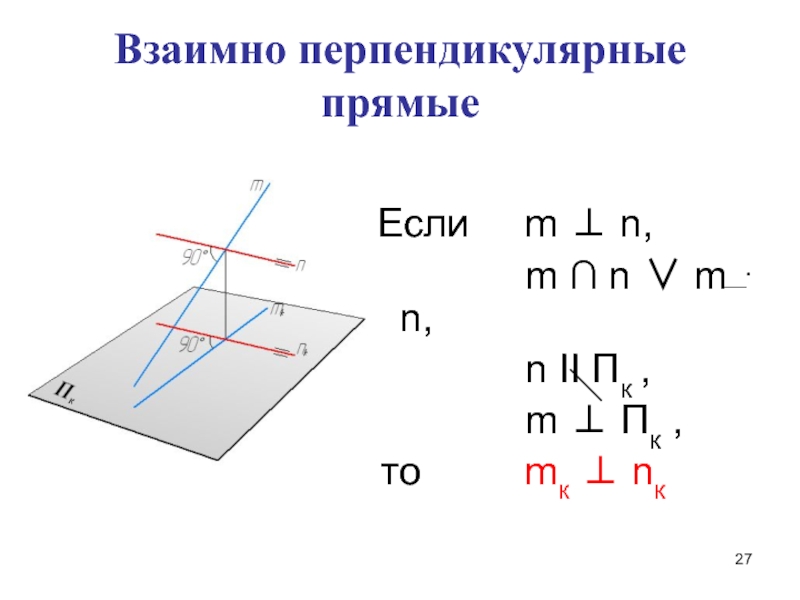
27. Взаимно перпендикулярные прямые Если m
28. m  n  m  n
29. m  n  m  n
30. Следы прямойСлед прямой – это точка пересечения
31. Построение горизонтального следа прямойl ∩ П1 =
32. Построение фронтального следа прямойl ∩ П2 =
33. Скачать презентанцию

Прямая линия

Главная
Разное
Раздел № 2 Солодухин Е.А

Слайды и текст этой презентации

Слайд 1Раздел № 2 Солодухин Е.А.
НАЧЕРТАТЕЛЬНАЯ
ГЕОМЕТРИЯ

Слайд 2Прямая линия

Слайд 3Способы задания прямой на эпюре
l (A,B)

Al
Bl
l (С,s)


Cl
l ll s

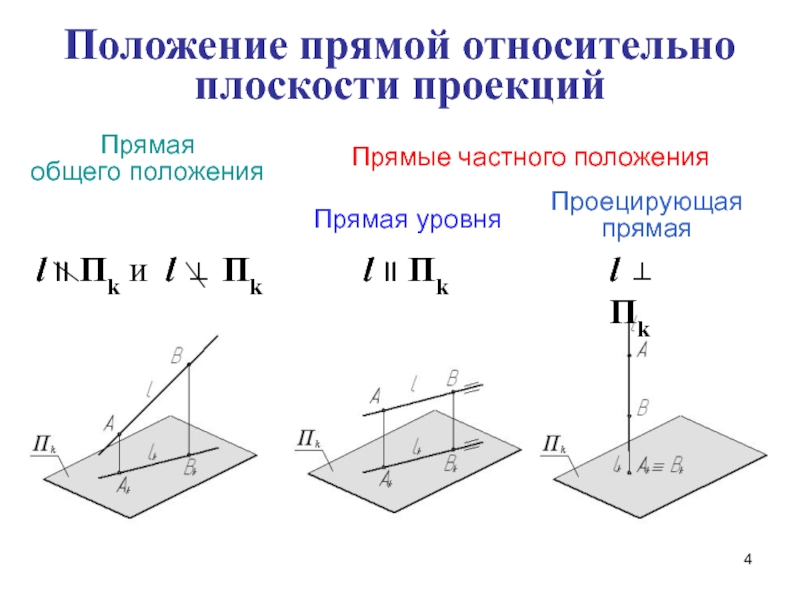
Слайд 4Положение прямой относительно плоскости проекций
Прямая
общего положения
Прямые частного положения
l II

Пk и l  Пk
l II Пk
l 

Пk

Прямая уровня

Проецирующая
прямая

Положение прямой относительно плоскости проекцийПрямая общего положенияПрямые частного положенияl II Пk и l  Пk l

Слайд 5

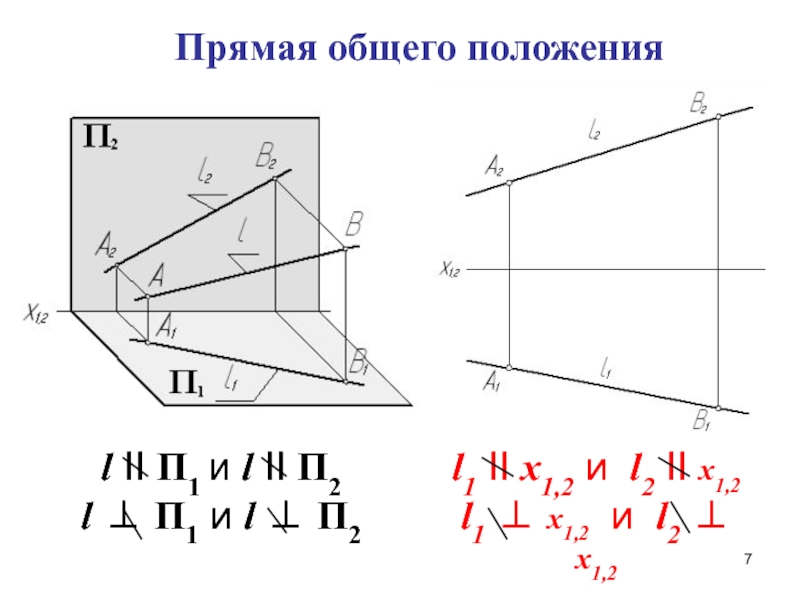
Слайд 6Прямая общего положения
Это прямая не параллельная и
не перпендикулярная ни одной

из плоскостей проекций
l II Пk и l  Пk

Прямая общего положения Это прямая не параллельная и не перпендикулярная ни одной из плоскостей проекцийl II Пk

Слайд 7l II П1 и l II П2
l  П1 и

l  П2
l1 II x1,2 и l2 II x1,2
l1 

x1,2 и l2  x1,2

Прямая общего положения

l II П1 и l II П2l  П1 и l  П2l1 II x1,2 и l2

Слайд 8Характерная особенность эпюра прямой общего положения – горизонтальная и фронтальная

проекции прямой не параллельны и не перпендикулярны координатной оси х1,2

Характерная особенность эпюра прямой общего положения – горизонтальная и фронтальная проекции прямой не параллельны и не перпендикулярны

Слайд 9Прямые частного положения
Это прямые параллельные или перпендикулярные одной из плоскостей

проекций
l II Пk  l  Пk

Слайд 10Прямая уровня
Это прямая параллельная какой-либо одной плоскости проекций
l II Пк

Слайд 11Горизонталь
Это прямая параллельная
горизонтальной плоскости проекций
l II П1  l

 h

ГоризонтальЭто прямая параллельная горизонтальной плоскости проекцийl II П1  l  h

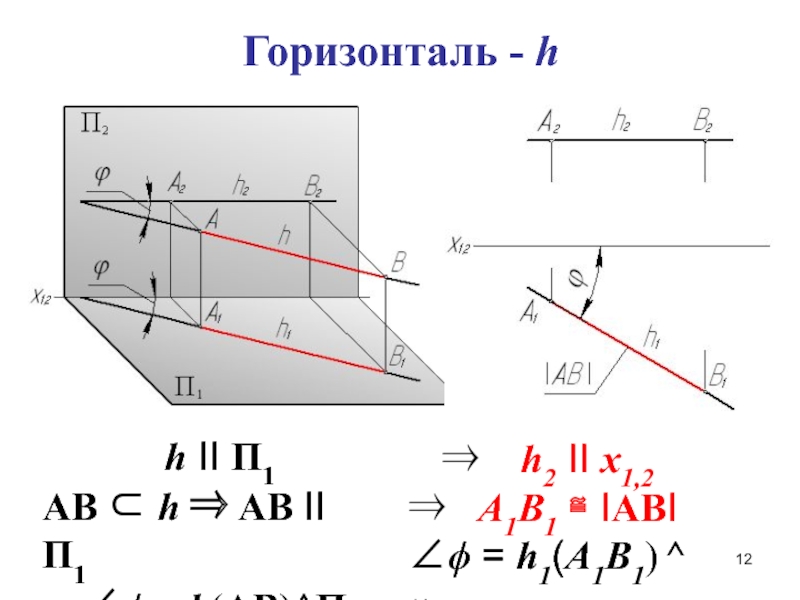
Слайд 12Горизонталь - h
h II П1
AB

 h  AB II П1
  h(AB)^П2

 h2 II x1,2
 А1В1  IABI
  h1(А1В1) ^ x1,2

Горизонталь - h h II П1AB  h  AB II П1

Слайд 13Фронталь
Это прямая параллельная
фронтальной плоскости проекций
l II П2  l

 f

ФронтальЭто прямая параллельная фронтальной плоскости проекцийl II П2  l  f

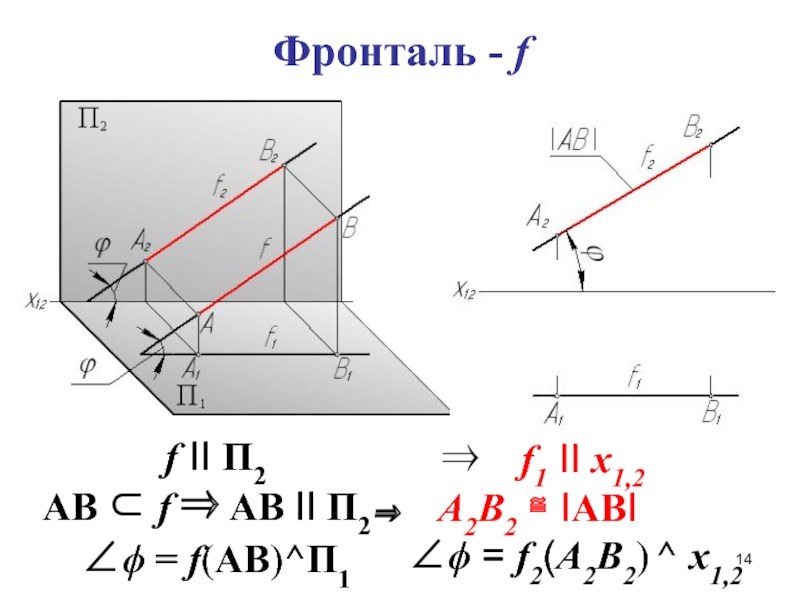
Слайд 14Фронталь - f
f II П2
AB

 f  AB II П2
  f(AB)^П1

 f1 II x1,2
А2В2  IABI
  f2(А2В2) ^ x1,2

Слайд 15Характерная особенность эпюра горизонтали и фронтали – одна из проекций

параллельна координатной оси х1,2

Слайд 16Профильная прямая - p
Это прямая параллельная профильной плоскости проекций П3

Слайд 17Проецирующая прямая
Прямая перпендикулярная одной из плоскостей проекций
m  Пк

Слайд 18Горизонтально-проецирующая прямая
Это прямая перпендикулярная
горизонтальной плоскости проекций
m  П1

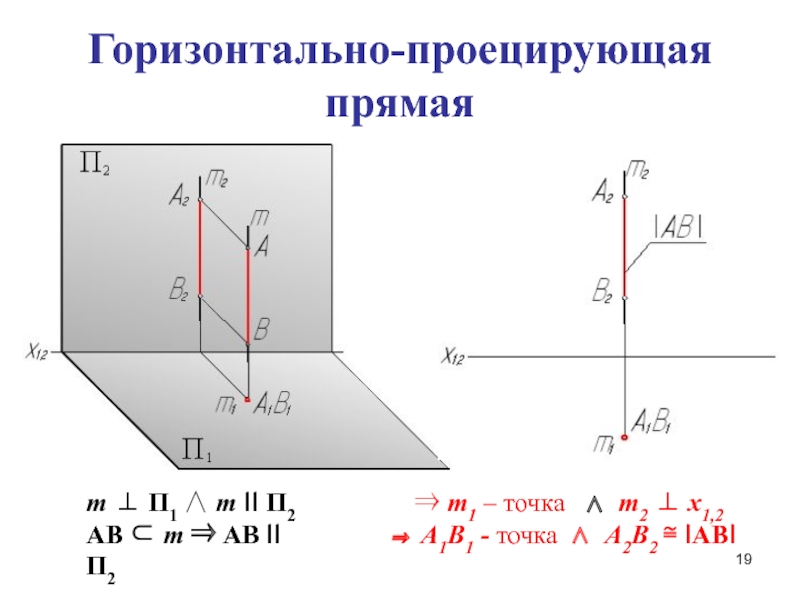
Слайд 19Горизонтально-проецирующая прямая
m  П1  m II П2
AB  m

 AB II П2
 m1 – точка

 m2  x1,2
А1В1 - точка  А2В2  IABI

Горизонтально-проецирующая прямаяm  П1  m II П2AB  m  AB II П2  m1

Слайд 20Фронтально-проецирующая прямая
Это прямая перпендикулярная
фронтальной плоскости проекций
m  П2

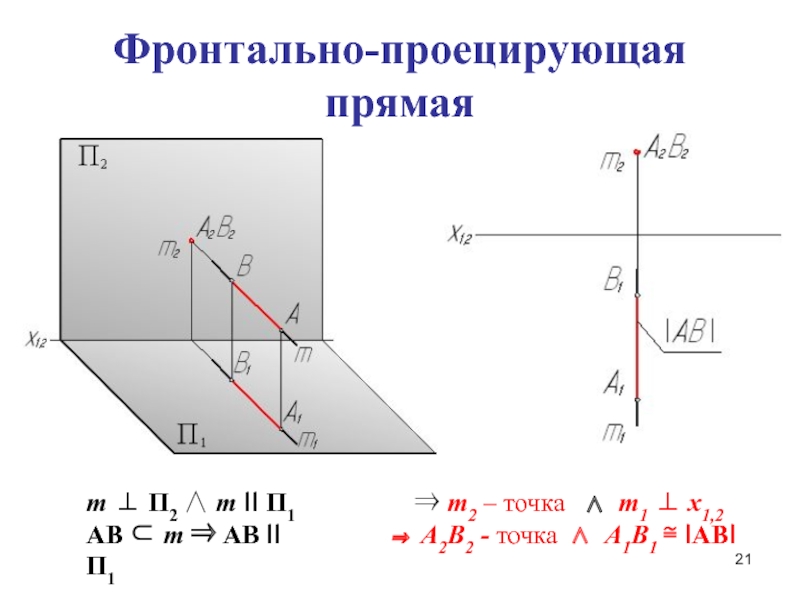
Слайд 21Фронтально-проецирующая прямая
m  П2  m II П1
AB  m

 AB II П1
 m2 – точка

 m1  x1,2
А2В2 - точка  А1В1  IABI

Фронтально-проецирующая прямаяm  П2  m II П1AB  m  AB II П1  m2

Слайд 22Характерная особенность эпюра проецирующей прямой – одна из проекций прямой

точка

Слайд 23Взаимное положение двух прямых

Слайд 24Пересекающиеся прямые
m ∩ n = D 
 mk ∩ nk=

Dk
m1 ∩ n1 = D1
m2 ∩ n2 = D2
D1D2 

x1,2

Пересекающиеся прямыеm ∩ n = D  mk ∩ nk= Dkm1 ∩ n1 = D1m2 ∩ n2

Слайд 25Параллельные прямые
m II n 
 mk II nk
m1 II n1
m2

II n2

Слайд 26Скрещивающиеся прямые
m  n  m II n  m

∩ n
Пары точек (1-2) и (3-4) – конкурирующие точки

Скрещивающиеся прямыеm  n  m II n  m ∩ n Пары точек (1-2) и (3-4)

Слайд 27Взаимно перпендикулярные прямые
Если m  n,

m  n  m

 n,
n II Пк ,
m  Пк ,
то mк  nк

Взаимно перпендикулярные прямые Если m  n, m 

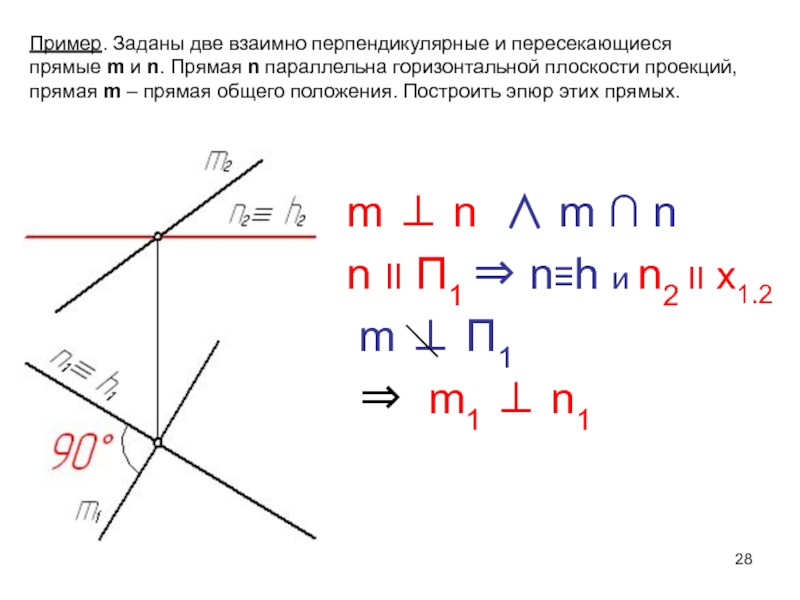
Слайд 28m  n  m  n
n II П1

 n≡h и n2 II х1.2
m  П1

 m1  n1

Пример. Заданы две взаимно перпендикулярные и пересекающиеся
прямые m и n. Прямая n параллельна горизонтальной плоскости проекций,
прямая m – прямая общего положения. Построить эпюр этих прямых.

m  n  m  n n II П1  n≡h и n2 II х1.2 m

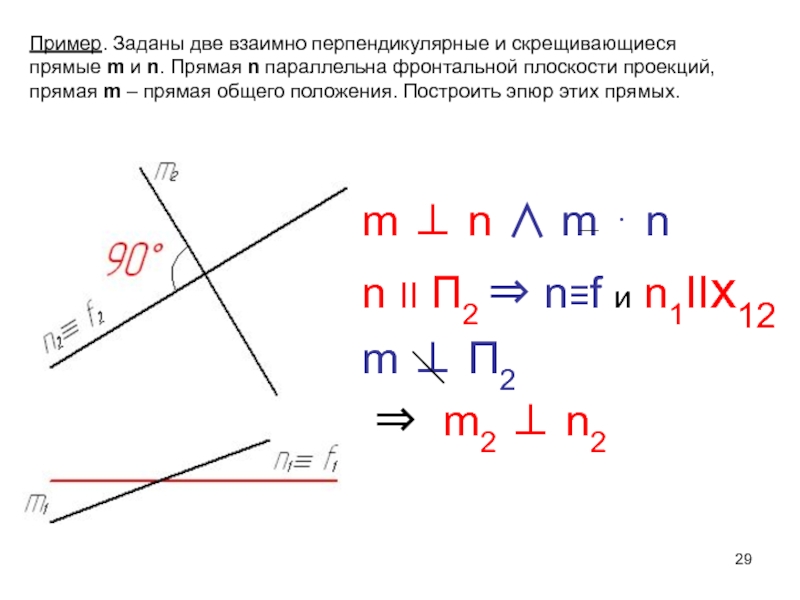
Слайд 29m  n  m  n
n II П2

 n≡f и n1IIх12
m  П2
 m2

 n2

Пример. Заданы две взаимно перпендикулярные и скрещивающиеся
прямые m и n. Прямая n параллельна фронтальной плоскости проекций,
прямая m – прямая общего положения. Построить эпюр этих прямых.

m  n  m  n n II П2  n≡f и n1IIх12m  П2 

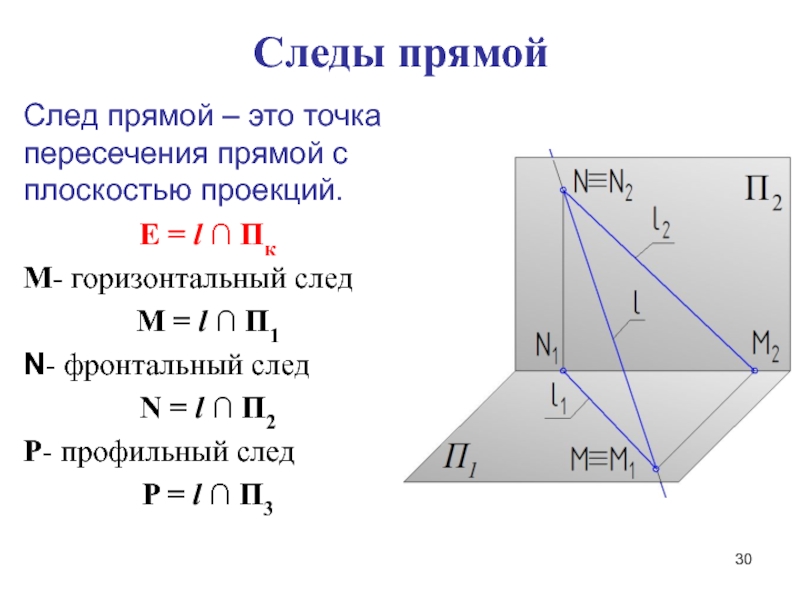
Слайд 30Следы прямой
След прямой – это точка пересечения прямой с плоскостью

проекций.
Е = l ∩ Пк
М- горизонтальный след
М = l ∩

П1
N- фронтальный след
N = l ∩ П2
Р- профильный след
P = l ∩ П3

Следы прямойСлед прямой – это точка пересечения прямой с плоскостью проекций.Е = l ∩ ПкМ- горизонтальный следМ

Слайд 31Построение горизонтального следа прямой
l ∩ П1 = М  М

П1; М  l
Требуется на прямой l найти точку М,

высота которой равна нулю.
На эпюре высота точки определяется расстоянием от оси х1,2 до фронтальной проекции точки.
Следовательно, решение задачи сводится к определению точки пересечения фронтальной проекции прямой с осью х1,2.

Мl  М1l1  М2l2
МП1  М1≡М  М2 х1,2


М2=l2 ∩ х1,2
М2М1  х1,2
М1l1

Построение горизонтального следа прямойl ∩ П1 = М  М П1; М  lТребуется на прямой l

Слайд 32Построение фронтального следа прямой
l ∩ П2 = N  N

П2; N  l
Требуется на прямой l найти точку N,

глубина которой равна нулю.
На эпюре глубина точки определяется расстоянием от оси х1,2 до горизонтальной проекции точки.
Следовательно, решение задачи сводится к определению точки пересечения горизонтальной проекции прямой с осью х1,2.

Nl  N2l1  N1l2
NП2  N2≡ N  N1 х1,2


N1=l1 ∩ х1,2
N1 N2  х1,2
N2l2

Построение фронтального следа прямойl ∩ П2 = N  N П2; N  lТребуется на прямой l

Скачать презентацию

Разделы презентаций

Раздел № 2 Солодухин Е.А

Содержание

Слайды и текст этой презентации

Слайд 1Раздел № 2 Солодухин Е.А.НАЧЕРТАТЕЛЬНАЯГЕОМЕТРИЯ

Слайд 2Прямая линия

Слайд 3Способы задания прямой на эпюреl (A,B) Al Bll (С,s)

 Cl l ll s

Слайд 4Положение прямой относительно плоскости проекцийПрямая общего положенияПрямые частного положенияl II

Пk и l  Пk l II Пk l 

Слайд 5

Слайд 6Прямая общего положения Это прямая не параллельная и не перпендикулярная ни одной

из плоскостей проекцийl II Пk и l  Пk

Слайд 7l II П1 и l II П2l  П1 и

l  П2l1 II x1,2 и l2 II x1,2l1 

Слайд 8Характерная особенность эпюра прямой общего положения – горизонтальная и фронтальная

проекции прямой не параллельны и не перпендикулярны координатной оси х1,2

Слайд 9Прямые частного положенияЭто прямые параллельные или перпендикулярные одной из плоскостей

проекцийl II Пk  l  Пk

Слайд 10Прямая уровняЭто прямая параллельная какой-либо одной плоскости проекцийl II Пк

Слайд 11ГоризонтальЭто прямая параллельная горизонтальной плоскости проекцийl II П1  l

 h

Слайд 12Горизонталь - h h II П1AB

 h  AB II П1   h(AB)^П2

Слайд 13ФронтальЭто прямая параллельная фронтальной плоскости проекцийl II П2  l

 f

Слайд 14Фронталь - f f II П2AB

 f  AB II П2   f(AB)^П1

Слайд 15Характерная особенность эпюра горизонтали и фронтали – одна из проекций

параллельна координатной оси х1,2

Слайд 16Профильная прямая - pЭто прямая параллельная профильной плоскости проекций П3

Слайд 17Проецирующая прямая Прямая перпендикулярная одной из плоскостей проекцийm  Пк

Слайд 18Горизонтально-проецирующая прямаяЭто прямая перпендикулярная горизонтальной плоскости проекцийm  П1

Слайд 19Горизонтально-проецирующая прямаяm  П1  m II П2AB  m

 AB II П2  m1 – точка

Слайд 20Фронтально-проецирующая прямаяЭто прямая перпендикулярная фронтальной плоскости проекцийm  П2

Слайд 21Фронтально-проецирующая прямаяm  П2  m II П1AB  m

 AB II П1  m2 – точка