Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Развитие пространственного воображения
Содержание
- 1. Развитие пространственного воображения
- 2. Формально - логический подход Наглядно - прикладной подход МетодикагеометрииРазвитие пространственного воображения как педагогическая проблема
- 3. Формально-логический подходОсновная задача:построение логического аппарата;упражнение дедуктивного
- 4. «Никогда ни одно научное
- 5. Наглядно-прикладной подход Авторы курса
- 6. «геометрия имеет своим
- 7. МоделированиеСредства наглядного обученияОбширная литератураПособия по преподаванию геометрии
- 8. Прохождение курса геометрии должно согласоваться:123С возрастными особенностями
- 9. В большей степени опираться на интуицию
- 10. Экспериментальные работы по исследованию пространственных представлений и пространственного воображения учащихся старших классов средней школы
- 11. №1. Вообразим себе куб,
- 12. D1C1A1B1DABCI пирамидаB(A1B1C1)C1A1B1DABCC1A1B1DABCD1D1III пирамидаS(A1B1C1D1)II пирамидаB(A1B1C1D1)S
- 13. Сколько граней имеет пирамида?Назовите равные грани
- 14. №2. Дан куб, в который вписан
- 15. Верное решение
- 16. IIIIIIIV №3. Кольцо рассечено плоскостью, проходящей через
- 17. Верное решение
- 18. 2 – полный ответ, 1
- 19. 1 – за верное
- 20. Выводы по работе №2:
- 21. Выводы по работе №3:
- 22. Выводы в преподавании геометрии 1. Учащиеся старших классов
- 23. 6. Изображение пространственных фигур применяется
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
Формально - логический подход
Наглядно
- прикладной подход
Методика
геометрии
Развитие
пространственного воображения как педагогическая проблема
Слайд 3
Формально-логический подход
Основная задача:
построение логического аппарата;
упражнение дедуктивного мышления учащихся.
Методическое направление основывается на совершенно противоположных принципах наглядного,
конкретного преподавания геометрии и частого обращения к прикладным вопросам.Слайд 4
«Никогда ни одно научное сочинение не имело
успеха, сравнимого с «Началами» Евклида. Исключительно по ним в течение
веков учили геометрии во всех математических школах; они переведены на все языки и на всех языках комментировались, – доказательство их исключительного превосходства» «Только розгами можно вогнать ученикам четыре первых теоремы евклидовых «Элементов», а пятая уже называется «Elefuga» – бегство несчастного!»
Слайд 5
Наглядно-прикладной подход
Авторы курса придерживались чисто эмпирических
методов изложения курса геометрии, пренебрегая его внутренним содержанием как дедуктивной
дисциплины. Доказательства геометрических теорем были заменены лабораторными методами нахождения законов этой науки.
Слайд 6
«геометрия имеет своим предметом пространственные
формы и количественные отношения действительного мира, т.е. весьма реальное содержание»
Важно,
чтобы:школьное обучение геометрии было основано на пространственном представлении всех геометрических образов и форм, свойства которых изучаются в курсе геометрии;
учащиеся видели эти геометрические образы в окружающей действительности и могли бы применять свою геометрию в практической жизни.
Слайд 7
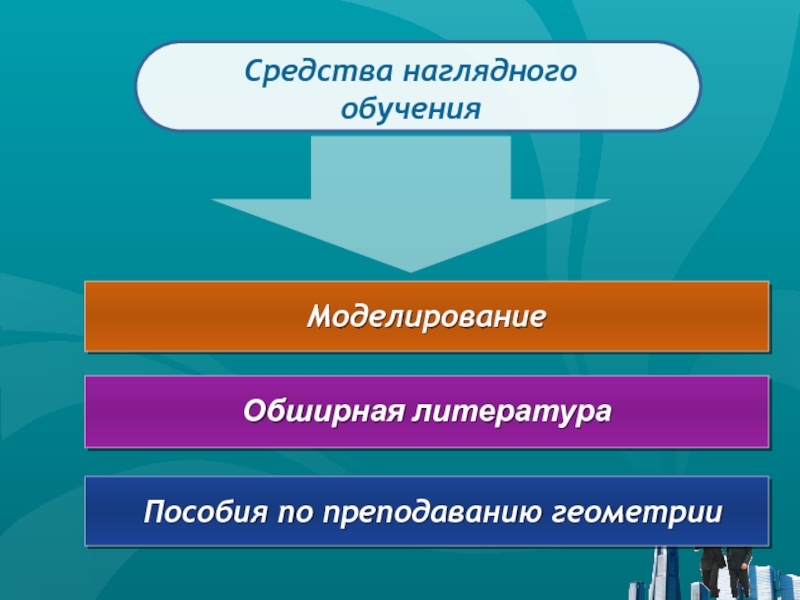
Моделирование
Средства наглядного обучения
Обширная литература
Пособия по преподаванию геометрии
Слайд 8Прохождение курса геометрии должно согласоваться:
1
2
3
С возрастными особенностями учащихся.
С развитием их
геометрических представлений.
Способностью воображать пространственные фигуры и делать логические умозаключения.
Слайд 9
В большей степени опираться на интуицию учащихся
Методы
преподавания
геометрии
должны:
Широко применять наглядность
в процессе изучения материала
Чаще делать чертежи изучаемых геометрических образов
Обращаться к
моделированиюСлайд 10
Экспериментальные работы по исследованию пространственных представлений и пространственного
воображения учащихся старших классов средней школы
Слайд 11
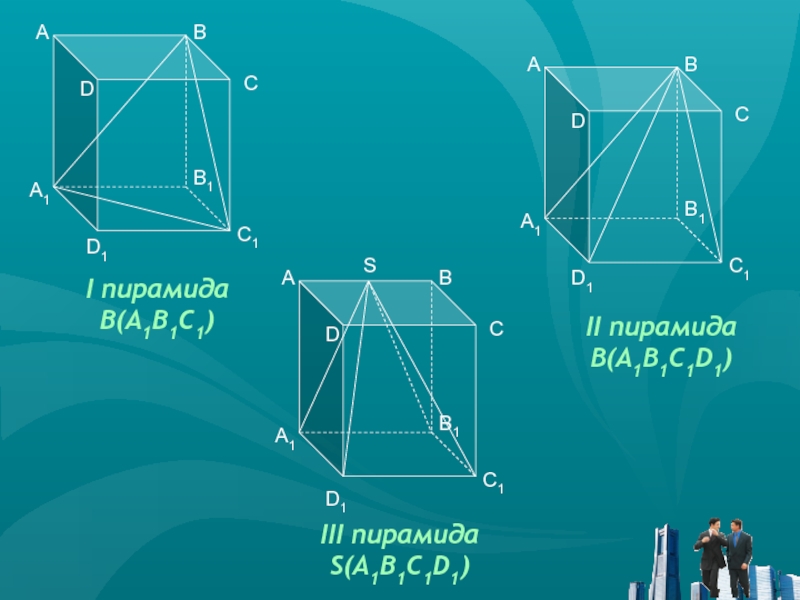
№1. Вообразим себе куб, верхнее основание которого
обозначено буквами ABCD, а нижнее основание обозначено соответственно буквами A1B1C1D1.
Причем, вершина A1 находится под вершиной A и т.д. В этом кубе построена пирамида, вершиной которой является точка B, а основанием служит треугольник A1B1C1.Кроме указанной пирамиды, вообразите вторую пирамиду. Она получается следующим образом при помощи того же самого куба ABCD (A1B1C1D1). Вершина второй пирамиды находится в точке B верхнего основания куба, а основанием пирамиды служит нижнее основание куба.
Наконец, вообразите еще третью пирамиду. Вершина третьей пирамиды находится в середине S ребра AB верхнего основания куба, а основанием служит нижнее основание куба A1B1C1D1.
Слайд 12
D1
C1
A1
B1
D
A
B
C
I пирамида
B(A1B1C1)
C1
A1
B1
D
A
B
C
C1
A1
B1
D
A
B
C
D1
D1
III пирамида
S(A1B1C1D1)
II пирамида
B(A1B1C1D1)
S
Слайд 13
Сколько граней имеет пирамида?
Назовите равные грани данной пирамиды.
Назовите равные
двугранные углы пирамиды.
Назовите равные стороны и равные углы в каждой
грани пирамиды.Назовите прямые (плоские и двугранные) углы пирамиды.
Слайд 14
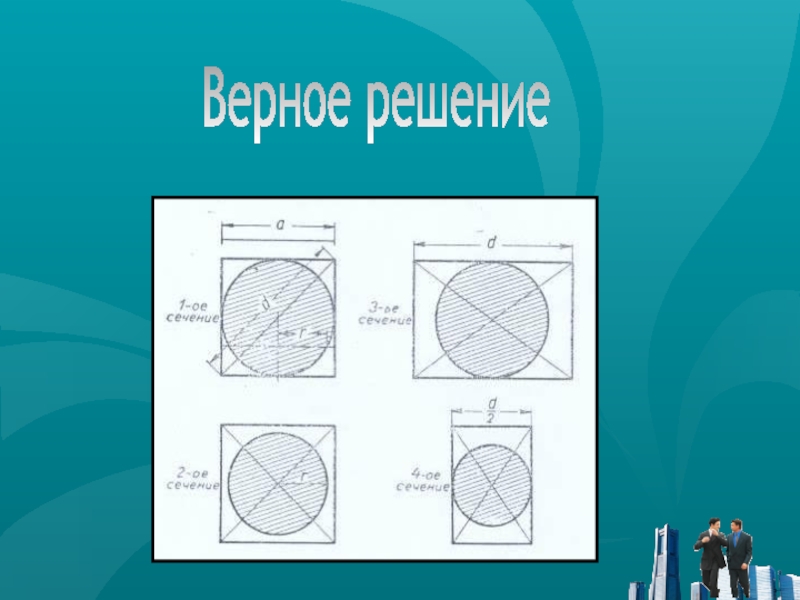
№2. Дан куб, в который вписан шар. Проведем четыре
сечения:
Через середину бокового ребра параллельно основанию.
На высоте четверти бокового ребра,
параллельно основанию.Диагональное сечение.
Через середину ребра верхнего основания, параллельно диагональному сечению.
(1)
(1)
(2)
(2)
(3)
(4)
(4)
(4)
Слайд 16
I
II
III
IV
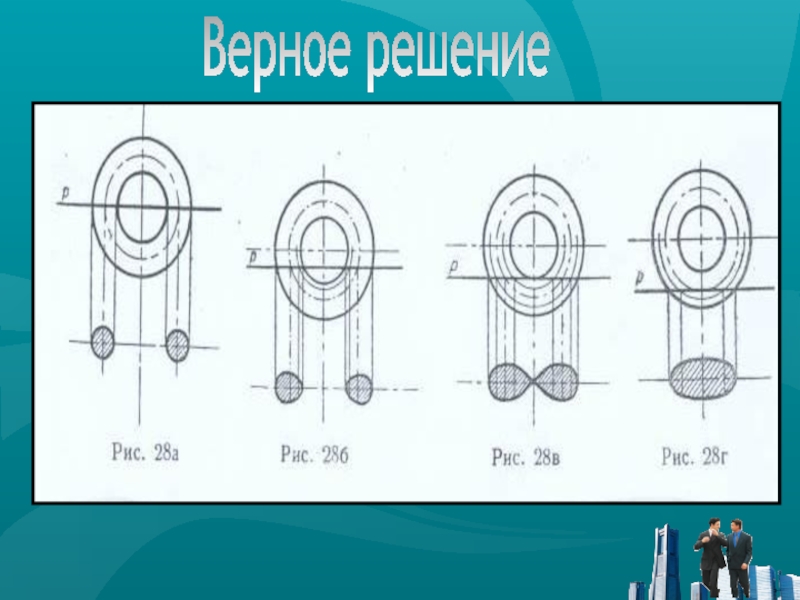
№3. Кольцо рассечено плоскостью, проходящей через ось вращения.
Это сечение обозначено цифрой I.
Секущая плоскость постепенно передвигается параллельно
самой себе сверху вниз и образует еще три сечения: сечение II, отстоящее от центра кольца на четверть радиуса его, сечение III, отстоящее от центра на половину радиуса, и сечение IV, отстоящее от центра на три четверти радиуса кольца.Слайд 18
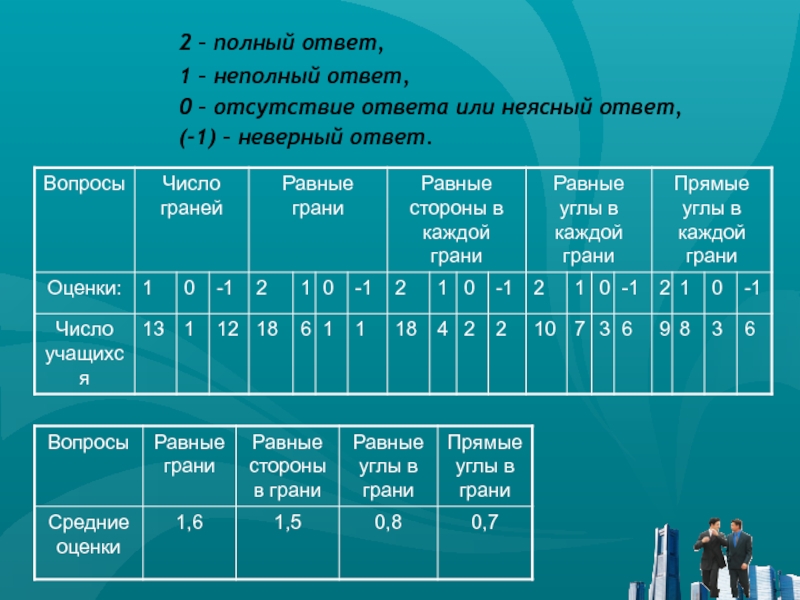
2 – полный ответ,
1 – неполный
ответ,
0 – отсутствие ответа или неясный ответ,
(-1) – неверный ответ.
Слайд 19
1 – за верное решение (
для 1-го и 3-го сечения),
2 – за верное решение (
для 2-го и 4-го сечения), 0 – за отсутствие решения или неясного решения,(-1) – за неверное решение.
Слайд 20Выводы по работе №2:
1. Следует отметить, что самый метод выполнения задания чисто графическим
путем, без вывода формул и вычислений, вызвал затруднения у учащихся и казался для них необычным. При обычном преподавании стереометрии в школах преобладают задачи вычислительного характера, в которых в готовые формулы подставляются данные значения. Неумение учащихся пользоваться пространственным представлением фигур и весьма простыми графическими приемами решения задач было причиной многих ошибок.2. Решение задач вызвало большой интерес среди учащихся старших классов.
Слайд 21Выводы по работе №3:
1. Для
выполнения этой работы учащиеся могли бы не обладать знаниями курса
геометрии, т.к. в этой работе они не могли бы применить этих знаний для построения искомых сечений кольца. Вопрос решался лишь в зависимости от развития пространственных представлений у учащихся.2. Проведенные работы показали, что большинство учащихся правильно понимали, в чем заключалось требуемое от них при выполнении этого задания. Большая часть учащихся смогла представить себе форму кольца и дать верное изображение простейших сечений. Однако более трудным оказалось 3-е сечение.
3. Большое разнообразие в выборе геометрических фигур и упражнений с пространственными фигурами могло бы содействовать дальнейшему развитию пространственного воображения учащихся.
Слайд 22Выводы в преподавании геометрии
1. Учащиеся старших классов школы имеют достаточно
отчетливые пространственные представления основных геометрических элементов и фигур.
2. Недостатком в
развитии пространственных представлений учащихся является их привычка к шаблонам.3. Обнаруживается привычка учащихся мыслить планиметрические фигуры лишь в плоскости чертежа, в не в произвольных положениях в пространстве.
4. Преподавание геометрии часто не устанавливает живой связи между зрительным восприятием формы предметов и их натуральными формами
5. Учащиеся почти не применяют графических методов решения задач, основанных на пространственном воображении.
Слайд 23
6. Изображение пространственных фигур применяется в преподавании лишь
для иллюстрации и по большей части ограничивается применением кабинетной проекцией
7. В школьном курсе не разработана методика решения задач на построение в пространстве (в частности, а) решение стереометрических задач на проекционном чертеже и б) решение стереометрических задач в воображении).
8. Преподавание геометрии в старших классах особенно нуждается в прочной опоре на пространственном представлении геометрических фигур и всех геометрических соотношений.