Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение неравенств методом интервалов. 8 класс
Содержание
- 1. Решение неравенств методом интервалов. 8 класс
- 2. 1.Какие неравенства соответствуют промежуткам:X
- 3. 2.Какие неравенства соответствуют геометрическим моделям:X ≥ - 4 -1
- 4. 3.Какие промежутки соответствуют геометрическим моделям:
- 5. Какой алгоритм применяется при решении неравенств методом
- 6. Чтобы решить неравенство вида
- 7. Например: решить неравенство
- 8. Метод интервалов применяют при решении других видов неравенств. Например,
- 9. Найдите решение неравенства: 1)
- 10. Слайд 10
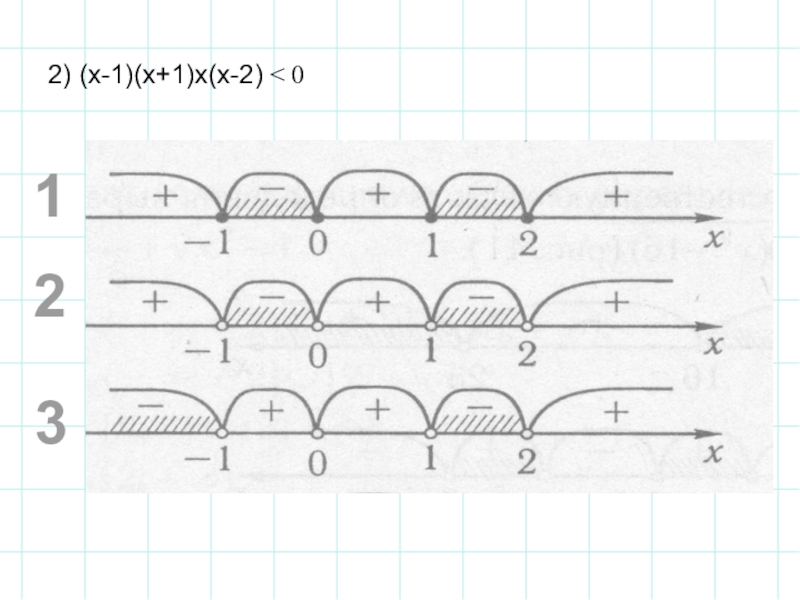
- 11. 2) (х-1)(х+1)х(х-2) < 0123
- 12. Ответ: в первом неравенстве 3 во втором неравенстве 2
- 13. Найти наименьшее целое решение неравенства: (решите
- 14. Найдите целое решение неравенства. В таблицу
- 15. № 675
- 16. Спасибо за внимание!Успехов!
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 5Какой алгоритм применяется при решении неравенств методом интервалов?
1) Преобразовать неравенство
(привести неравенство) к одному из видов: Р(х)>0, Р(х)< 0, Р(х)
0, Р(х) 0;2) решить уравнение Р(х)=0, т.е. находим нули функции соответствующей функции;
3) значение корней уравнения отметить на числовой оси и через отмеченные точки провести волнообразную линию;
Алгоритм:
4) определить знак соответствующей функции на одном из интервалов и на этом интервале поставим соответствующий знак: «+» или «-»;
5) на следующих интервалах поставим знаки, чередуя их в том случае, когда уравнение не имеет повторяющихся корней или корни повторяются нечетный раз; когда уравнение имеет корни, повторяющиеся четный раз , то на интервалах, которые ограничиваются значением этого корня, знаки будут одинаковыми;
6) в качестве ответа в зависимости от вида неравенства (>,<, , )
берутся те интервалы, на которые поставлен соответствующий знак.
Слайд 6Чтобы решить неравенство вида
(х+а)(х+с)(х+b) >0 методом интервалов надо:
1) Найти корни уравнения
(х+а)(х+с)(х+b) = 0 2) Корни уравнения отметить на числовой оси - ось разобьется на интервалы
3) Определить знак (+ или -) выражения (х+а)(х+с)(х+b) на каждом из интервалов;
4) Выбрать подходящие интервалы (в зависимости от знака < или > ) и записать ответ.
Метод интервалов.
Слайд 7Например: решить неравенство
(х + 5)(х – 6) ≥ 0
Решение: 1) решим
уравнение (х + 5)(х – 6) = 0.х+5=0 или х-6=0 , значит х₁= -5, а х₂ = 6
2) отмечаем полученные корни на оси и определяем знак выражения (х+5)(х-6) на полученных интервалах (для этого берём любое число из 1-го интервала, например -8, и подставляем его вместо х, вычисляем и ставим знак результата на интервал, то же делаем на других интервалах)
3) запишем ответ: (-∞; -5]U[6; +∞)
Слайд 13Найти наименьшее целое решение неравенства: (решите неравенство и из полученного
ответа выберите наименьшее целое число)
< 0Слайд 14Найдите целое решение неравенства. В таблицу под порядковым номером неравенства
поставьте букву, обозначающую правильный ответ.
1)
4) х² - 16х < - 63 (у – 4)(у – 2) < 0 5) (2у-3)(2у-5)<0
3) х²(х-11)(х-13) < 0 6) (3х-12)(6-х) > 0
Е
Л
Б
А
С
Ы
Задание: зашифрованное слово