Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
RSA
Содержание
- 1. RSA
- 2. RSAФормирование ключаp и q – большие простыеN=p*qφ(N)=(p-1)*(q-1)Выбор K
- 3. RSAШифрование M-сообщение в виде числа
- 4. RSAПояснение к расшифрованию:M’=Ek=MKk=M l φ(N)+1=M*(Mφ(N)) l= =M*1=M
- 5. Сложность вычислений RSAФормирование ключа:Нахождение простых p и
- 6. Стойкость RSAНахождение k из K так как
- 7. Стойкость RSAНахождение k из K, M, E,
- 8. Стойкость RSAОпределение M из E без нахождения
- 9. Слабые ключи RSAE = M K mod N = M mod N, т.е.
- 10. Особенности использования RSAМалые ключиМалые сообщенияСоставные p q (требования к выбору p q)…
- 11. Шифр Эль ГамаляФормирование ключа:Находят простое число pВыбирают целое число b , 0
- 12. Эль ГамаляШифрование:выбирает целое число K’ (0
- 13. Эль ГамаляРасшифрование:M = – a mod p Пояснение к расшифрованию: –a = b –aK’ mod p ; –a = M y K’ b –aK’ = M b аK’ b –aK’ = M mod p.
- 14. Эль ГамаляОсобенности:Так как K’ выбирается случайно, то
- 15. Криптосистемы на эллиптических кривых В общем случае
- 16. Слайд 16
- 17. Операции на Э.к.Определим операцию сложения точек на
- 18. Слайд 18
- 19. СложениеТочка 0 - нулевой элемент.Так, 0 =
- 20. СложениеДля сложения двух точек P и Q
- 21. Слайд 21
- 22. Операции на Э.к.Если прямая - касательная к
- 23. ШифрованиеИсходные параметры – сама э.к. и исходная
- 24. ШифрованиеШифрованиеСообщение представляется точкой M на э.к.A выбирает
- 25. Свойства асимметричных системУпрощение распределения ключейУменьшение числа ключей
- 26.
- 27. Гибридная криптосистемаАсимметричные системы+ упрощение распределения ключа– медленная скоростьСимметричные системы– сложное распределения ключа+ высокая скорость
- 28. Гибридная криптосистемаAKсимм1.Формирование ключей:ВKВ kВ2. Шифрование:E0=fасимм(Kсимм;KB)Kсимм= gассим(E0;kB)(E;E0)3. Расшифрование:М= gсимм(E;Kсимм)E =fсимм (M; Kсимм)KBЦифровой конверт
- 29. Скачать презентанцию
RSAФормирование ключаp и q – большие простыеN=p*qφ(N)=(p-1)*(q-1)Выбор K
Слайды и текст этой презентации
Слайд 4RSA
Пояснение к расшифрованию:
M’=Ek=MKk=M l φ(N)+1=M*(Mφ(N)) l=
=M*1=M mod N
Mφ(N)=1 mod N
– справедливо только для НОД(M,N)=1,
справедливость расшифрования может быть показана
и для НОД(M,N)>1a*b=1modp
a*b=l*p+1
Слайд 5Сложность вычислений RSA
Формирование ключа:
Нахождение простых p и q – «простая»
вероятностный тест и « небольшой» перебор.
N=p*q; (p-1)*(q-1) «простые»
НОД(K, φ(N)) -
«простая» - алгоритм Эвклидаk – обратный элемент для K - «простая» - расширенный алгоритм Эвклида
Шифрование, расшифрование
Возведение в степень по mod – «простые » – быстрое возведение в степень.
Слайд 6Стойкость RSA
Нахождение k из K так как ключи каким-то образом
связанны:
Kk=1mod φ(N), т.е. если если известно φ(N), то k найти
«просто».φ(N)=(p-1)*(q-1), т.е. если если известны p и q то k найти «просто».
p и q можно определить из известного N методом разложения на множители, но это «сложно».
Слайд 7Стойкость RSA
Нахождение k из K, M, E, N, f() g()
Из
соотношения: M=Ekmod N можно попытаться определить k:
Противник сам формирует произвольное
сообщение ME=MKmod N находит криптограмму для сообщения M.
Определяет k=logEM mod N
«Сложно» – дискретное логарифмирование.
Слайд 8Стойкость RSA
Определение M из E без нахождения ключа:
Перехваченная криптограмма последовательно
возводится в степень открытого ключа по mod N^
E0=E – перехваченная
криптограммаEi=(Ei-1)Kmod N
Ek=E – если Ek совпадает с исходной E, то Ek-1 – зашифрованное сообщение:
Ek=(Ek-1)Kmod N аналогично E=MKmodN
Каждая операция возведения в степень простая, однако общее число шагов необозримо большое.
Слайд 9Слабые ключи RSA
E = M K mod N = M mod N,
т.е. шифрование фактически не изменяет
сообщений.
Для устранения недостатка при формировании ключей используют сильные простые:
p=2p’-1
q=2q’-1, p’
q’ – простые.
Слайд 10Особенности использования RSA
Малые ключи
Малые сообщения
Составные p q
(требования к выбору
p q)
…
Слайд 11Шифр Эль Гамаля
Формирование ключа:
Находят простое число p
Выбирают целое число b
, 0
ключ(a,p) секретный ключ.
Слайд 13Эль Гамаля
Расшифрование:
M = – a mod p
Пояснение к расшифрованию:
–a = b –aK’ mod p ;
–a = M y K’ b –aK’ = M b аK’ b –aK’ = M mod p.
Слайд 14Эль Гамаля
Особенности:
Так как K’ выбирается случайно, то криптограмма каждый раз
разная, даже для одинаковых сообщений*.
Криптограмма в два раза больше сообщения.
Алгоритм
широко используется, во многих случаях заменяя RSA.*(должно быть различным для разных сообщений, иначе возможен взлом)
Слайд 15Криптосистемы на эллиптических кривых
В общем случае уравнение эллиптической кривой
Е имеет вид:
y2 + axy + by =
x3 + cx2 + dx + e (a,b,c,d,e – целые) Пример:
y2 + y = x3 - x2
Точки с целыми координатами : А (0, 0), В (1, -1), С (1, 0) и D (0, -1)
Слайд 17Операции на Э.к.
Определим операцию сложения точек на эллиптической кривой:
На плоскости
существует бесконечно удаленная точка 0, в которой сходятся все вертикальные
прямые.Будем считать, что касательная к кривой пересекает точку касания два раза.
Если три точки эллиптической кривой лежат на прямой линии, то их сумма есть 0.
Слайд 19Сложение
Точка 0 - нулевой элемент.
Так, 0 = -0
для любой точки
Р на кривой Р + 0 = Р.
Вертикальная линия пересекает
кривую в двух точках с одной и той же координатой х:S = (x, y) и T = (x, -y).
Эта прямая пересекает кривую и в бесконечно удаленной точке,т.е.:
Р1 + Р2 + 0 = 0 и Р1 = -Р2.
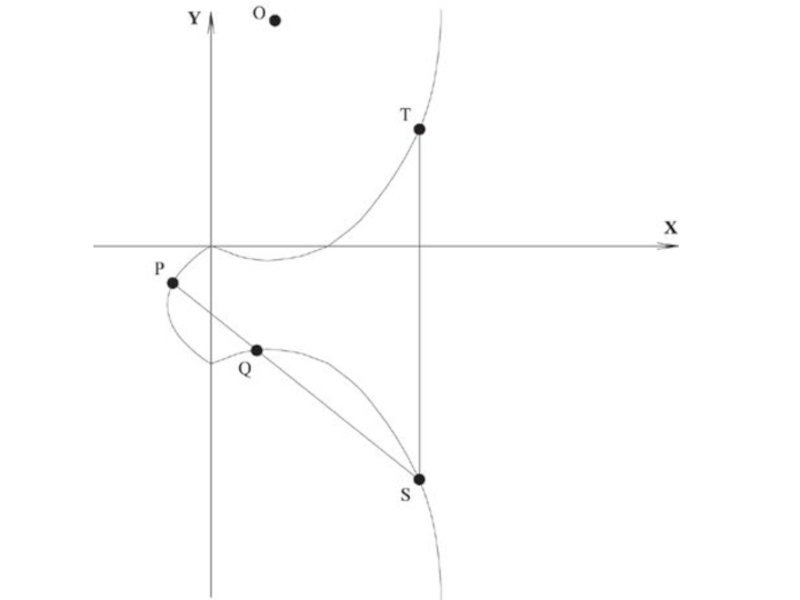
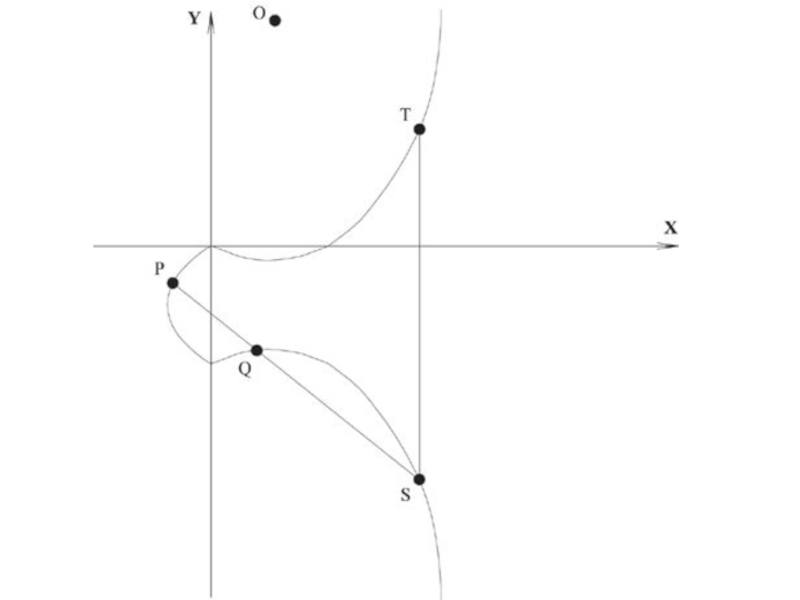
Слайд 20Сложение
Для сложения двух точек P и Q (см. рисунок) с
разными координатами х, следует провести через эти точки прямую и
найти точку пересечения ее с эллиптической кривой.Если прямая не является касательной к кривой в точках P или Q, то существует только одна такая точка, обозначим ее S.
P + Q + S = О
Следовательно,
P + Q = -S
P + Q = T
Слайд 22Операции на Э.к.
Если прямая - касательная к кривой в точке
P или Q, то в этом случае:
S = P
или S = Q. Удвоение точки Q:
необходимо провести касательную в точке Q и найти другую точку пересечения S с эллиптической кривой.
Q + Q = 2 × Q = -S.
Операция сложения подчиняется всем обычным правилам сложения.
Умножение точки Р на k (k>0) определяется как сумма k точек Р.
Слайд 23Шифрование
Исходные параметры – сама э.к. и исходная точка G на
ней.
Формирование ключей:
Выбирают точку: k (секретный ключ)
Вычисляют: K=k*G
Слайд 24Шифрование
Шифрование
Сообщение представляется точкой M на э.к.
A выбирает k’ – случайное
положительное число.
Криптограмма: E=(k’*G, M+k’*K)=(x,y)
Расшифрование:
M=y-k*x
Пояснение
[M+k’*K]-[k*(k’*G)]=
= M+k’*(k*G)- k*(k’*G)=M
![ШифрованиеШифрованиеСообщение представляется точкой M на э.к.A выбирает k’ – случайное положительное число.Криптограмма: E=(k’*G, M+k’*K)=(x,y)Расшифрование:M=y-k*xПояснение[M+k’*K]-[k*(k’*G)]= = M+k’*(k*G)- k*(k’*G)=M](/img/thumbs/47fe9b35fe04462e5c4c738df9852c8e-800x.jpg "RSA ШифрованиеШифрованиеСообщение представляется точкой M на э.к.A выбирает k’ – случайное положительное")
Слайд 25Свойства асимметричных систем
Упрощение распределения ключей
Уменьшение числа ключей при большом количестве
пользователей
Применение не только для шифрования
Прозрачнее криптоанализ (проще оценить стойкость)
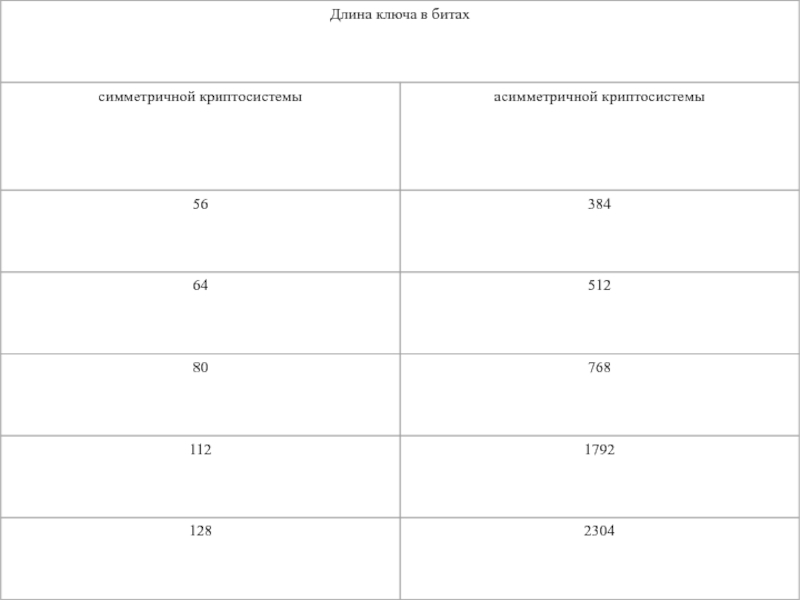
Большие длины
ключейМедленность преобразований (в десятки раз, если сравнивать с DES).
Слайд 27Гибридная криптосистема
Асимметричные системы
+ упрощение распределения ключа
– медленная скорость
Симметричные системы
– сложное
распределения ключа
+ высокая скорость
Слайд 28Гибридная криптосистема
A
Kсимм
1.Формирование ключей:
В
KВ kВ
2. Шифрование:
E0=fасимм(Kсимм;KB)
Kсимм= gассим(E0;kB)
(E;E0)
3. Расшифрование:
М= gсимм(E;Kсимм)
E
=fсимм (M; Kсимм)
KB
Цифровой конверт
