Слайд 1Лекция 3-4. Системы массового обслуживания.
План.
Марковские процессы и потоки событий.
Системы массового
обслуживания (СМО): структура, классификация, эффективность работы.
Одноканальная СМО с отказами.
Многоканальная СМО
с отказами.
Многоканальная СМО с ожиданием и ограничением на длину очереди.
Одноканальная СМО с ожиданием и ограниченной очередью.
Многоканальная СМО с ожиданием и неограниченной очередью.
Одноканальная СМО с ожиданием и неограниченной очередью
Слайд 21.Марковские процессы и потоки событий.
Теория массового обслуживания в
качестве аппарата использует понятия теории случайных величин:
=
Случайный процесс
дискретный
непрерывный
= Марковский случайный процесс
Слайд 31.Марковские процессы и потоки событий.
= Поток
без последействия
регулярный
ординарный
стационарный
пуассоновский
= Интенсивность
потока
Слайд 41.Марковские процессы и потоки событий.
Теорема. Для простейшего потока
событий с интенсивностью λ случайное число событий x(τ)=m (m=1,2,…), наступающих
за промежуток времени τ , распределено по закону Пуассона
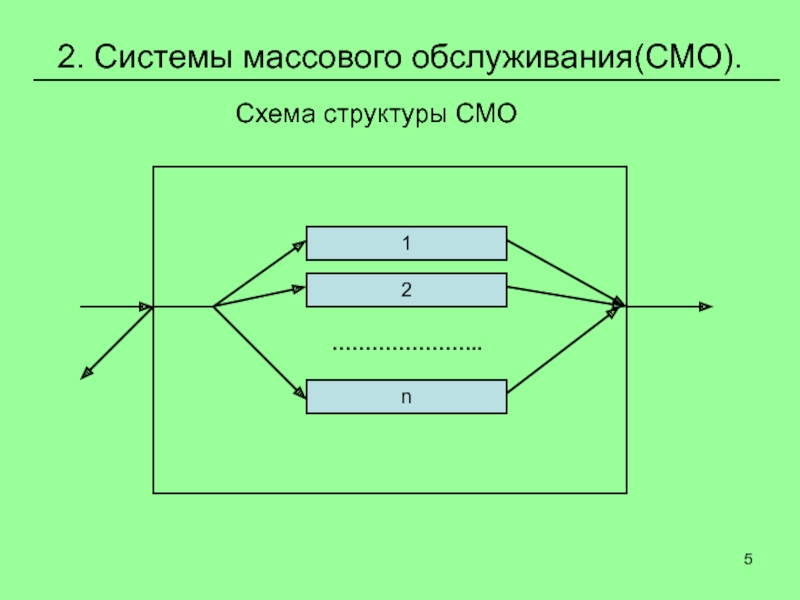
Слайд 52. Системы массового обслуживания(СМО).
Схема структуры СМО
Слайд 62. Системы массового обслуживания(СМО).
Основные элементы СМО:
Входной поток
заявок
Очередь
Каналы обслуживания
Выходной поток заявок
Слайд 72. Системы массового обслуживания(СМО).
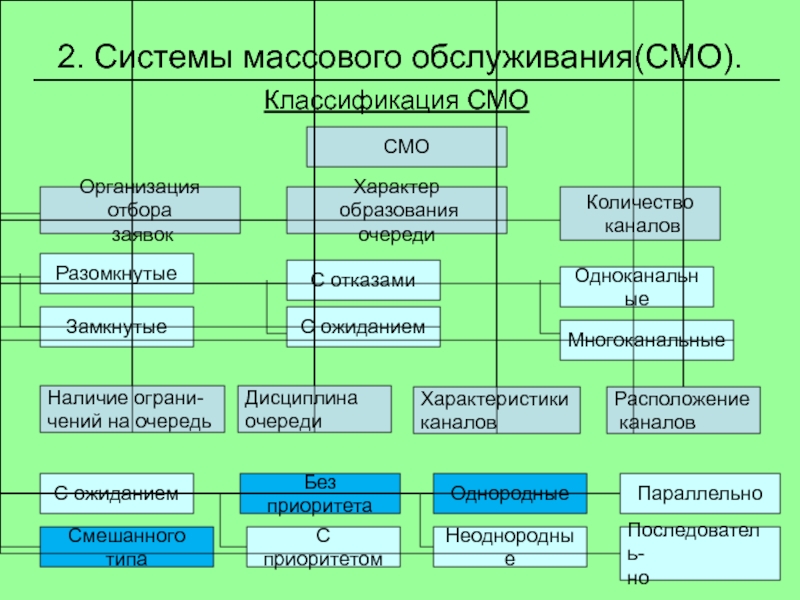
Классификация СМО
СМО
Слайд 82. Системы массового обслуживания(СМО).
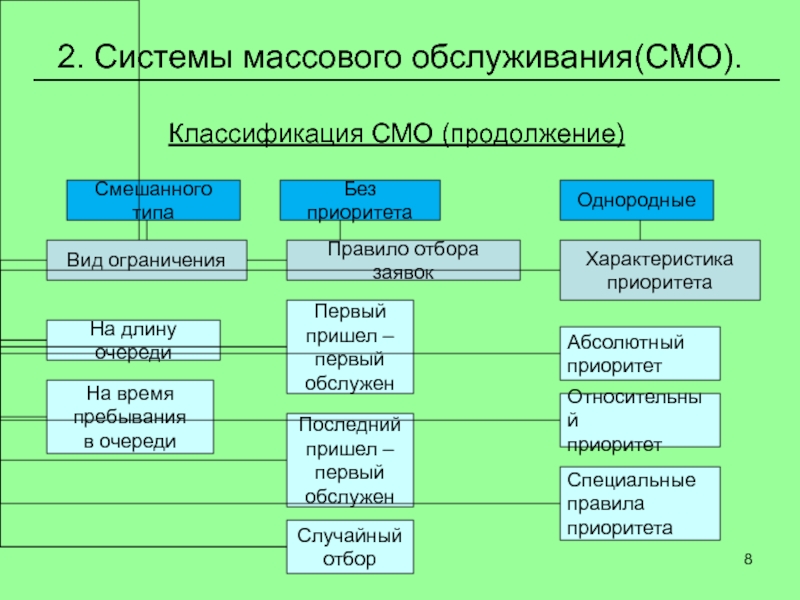
Классификация СМО (продолжение)
Слайд 92. Системы массового обслуживания(СМО).
Показатели эффективности работы СМО:
Абсолютная
пропускная способность (А);
Относительная пропускная способность (Q);
Приведенная интенсивность (
);
Средняя продолжительность периода занятости СМО (время обслуживания заявок);
Коэффициент использования СМО (время обслуживания заявок/время работы системы).
Слайд 102. Системы массового обслуживания(СМО).
Показатели качества обслуживания заявок:
Среднее
время ожидания заявки в очереди (Tline);
Среднее время пребывания заявки
в СМО (Tsys );
Вероятность отказа заявки в обслуживании без ожидания;
Вероятность немедленного приема заявки;
Закон распределения времени ожидания заявки в очереди в СМО;
Среднее число заявок в очереди (Nline);
Среднее число заявок, находящихся в СМО (Nsys).
Слайд 113. Одноканальная СМО с отказами.
Граф состояний СМО
Система уравнений
Колмогорова
Слайд 123. Одноканальная СМО с отказами.
Нормировочное условие
Предельные значения вероятностей состояния СМО
Слайд 133. Одноканальная СМО с отказами.
Основные характеристики работы СМО
Относительная пропускная способность
(Q)
Абсолютная пропускная способность (A)
Вероятность отказа в обслуживании заявки, когда канал
занят:
Слайд 143. Одноканальная СМО с отказами.
Основные характеристики работы СМО
Среднее время обслуживания
заявки:
Среднее время простоя канала:
Среднее время пребывания заявки в системе:
Слайд 15Пример: АТС имеет одну линию, на которую в среднем приходит
0.8 вызова в минуту. Среднее время разговора 2 минуты. Вызов,
пришедший во время разговора, не обслуживается. Считая потоки вызовов пуассоновскими найти абсолютную и относительную пропускную способности станции, вероятность отказа абоненту.
Решение:
Интенсивность потока обслуживания
μ = 1/tобс=1/2=0.5 выз./мин.
Интенсивность потока заявок
λ = 0.8 выз./мин.
Слайд 16Относительная пропускная способность
Q = p0 = μ /(λ+μ) = 0.5/(0.5+0.8)
=0.385
Абсолютная пропускная способность
А = λ*Q = 0.8*0.385 = 0.308
выз./мин.
Вероятность отказа в обслуживании
p1 = 1 - p0 = 1- 0.385 = 0.615
Слайд 17Пример: Телефонная станция имеет одну линию, на которую в среднем
приходит 0.9 вызова в минуту. Производительность линии 1.5выз./мин. Вызов, пришедший
во время разговора, не обслуживается. Считая потоки вызовов пуассоновскими найти абсолютную пропускную способности станции, среднее время обслуживания одного вызова, вероятность отказа в обслуживании, среднее время пребывания заявки в системе.
Решение:
Интенсивность потока обслуживания
μ = 1.5 выз./мин.
Интенсивность потока заявок
λ = 0.9 выз./мин.
Слайд 18Среднее время обслуживания одного вызова
tобс = 1/μ=1/1.5=0.67мин.
Абсолютная пропускная способность
А =
λ *μ/(λ+μ)= 0.9*1.5/(0.9+1.5) = 0.563 выз./мин.
Вероятность отказа в обслуживании
p1 =
λ /(λ+μ)= 0.9/(0.9+1.5) = 0.375
Время пребывания заявки в системе:
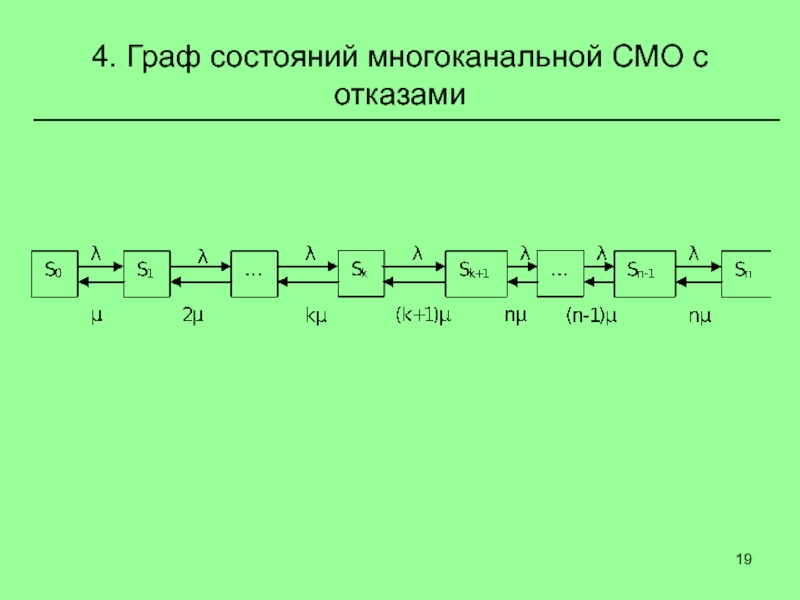
Слайд 194. Граф состояний многоканальной СМО с отказами
Слайд 20Уравнение Колмогорова для многоканальной СМО
Нормировочное условие
Слайд 21Предельные вероятности системы
Предельный режим работы СМО
Слайд 22Уравнение нормировки в стационарном виде
Приведенная интенсивность входящего потока (измеряется в
эрлангах):
Слайд 23Решение системы уравнений:
Формулы Эрланга
Слайд 24Основные характеристики СМО
Отказ в обслуживании заявки
Вероятность обслуживания заявки
Относительная пропускная способность
Q
= ps
Абсолютная пропускная способность
A = λQ = λ(1- pn)
Слайд 25Среднее число занятых каналов
Среднее время пребывания заявки в СМО
Слайд 26Пример: в отделении банка на обслуживании клиентов работают 3 оператора.
Среднее время обслуживания одного клиента оператором – 12 минут. В
среднем за час в банк обращаются 15 клиентов. Если все операторы заняты, клиенты банком не обслуживаются.
I. Найти основные средние характеристики работы отделения банка, а также вероятность того, что не менее двух операторов простаивают.
II. Рассчитать, как изменятся характеристики работы СМО, если операторы будут тратить на обслуживание клиентов 10 минут.
III. Определить минимальную среднюю производительность операторов, чтобы вероятность обслуживания клиентов банка была бы не ниже 0,9
Слайд 27Решение:
I. Число каналов: n=3
Интенсивность входного потока заявок: λ = 15
клиентов/час
Интенсивность одного канала обслуживания μ =1/tобс= 1/(12/60) = 5 клиентов/час
Тогда
приведенная интенсивность: ρ = λ/ μ =15/5=3
Вероятность простоя системы:
p0 = 1/(1+3+3^2/2+3^3/6) = 0,077
Вероятность отказа:
pr = p3 = p0*3^3/6 = 0,346
Относительная пропускная способность:
Q = pS = 1 – pr = 1- 0,346 = 0,654
Абсолютная пропускная способность:
A = λ*Q= 9,81 клиент/час
Среднее число занятых каналов Ňsys= A/μ = 1,962
Среднее время пребывания заявки в СМО
Tsys = Nsys/ λ = 0,131 ч = 7,85 мин.
Слайд 28Вероятность того, что не менее 2 операторов простаивают: p0 +
p1 = 0,077*(1+3) = 0,308
II. Интенсивность одного канала обслуживания μ
= 6 клиентов/час
Тогда ρ = λ/ μ =15/6=2,5
p0= 1/(1+2,5+2,5^2/2+2,5^3/6) = 0,108
pr= p3 = p0*2,5^3/6 = 0,28
Q = p3 = 1 – pr = 1- 0,28 = 0,72
A = λ*Q= 10,8 клиент/час
Среднее число занятых каналов Ňsys= A/μ = 1,8
Среднее время пребывания заявки в СМО
Tsys = Nsys/ λ = 0,12 ч = 7,2 мин.
Слайд 29III. Из условия следует 1- pn >=0,9 pn
определяем:
Ответ: μ >= 12
Слайд 30Граф состояний n-канальной СМО с ограничением на длину очереди m
5.
Многоканальная СМО с ожиданием и ограничением на длину очереди
Слайд 31Основные соотношения
Уравнения Колмогорова для многоканальной СМО с ожиданием и ограничением
на длину очереди
Слайд 32Нормировочное условие:
Показатель нагрузки на один канал
Слайд 33Решение системы уравнений:
Упрощенная формула:
Слайд 34Остальные предельные вероятности:
Слайд 35Основные характеристики СМО
Вероятность отказа:
Вероятность приема заявки:
Абсолютная пропускная способность:
Слайд 36Среднее число занятых каналов
Среднее число заявок в очереди
Среднее число заявок,
находящихся в системе
Слайд 37Среднее время обслуживания заявки
Среднее время ожидания заявки в очереди
Среднее время
пребывания заявки в СМО
Слайд 38Пример. В пункте валютного обмена работают два оператора, каждый из
которых обслуживает клиента в среднем за 2,5 минуты. По условиям
безопасности в помещении пункта может находиться одновременно не более 5 человек, включая обслуживаемых клиентов. Если помещение заполнено, то очередной клиент не становится в очередь, а уходит. В среднем клиенты приходят каждые 2 минуты. Найти основные характеристики работы обменного пункта.
Слайд 39Решение:
Число каналов: n= 2
Длина очереди m =3
Интенсивность входного потока заявок:
λ = 0,5 клиент/мин.
Интенсивность потока обслуживания μ = 1/2.5 =
0,4 клиент/мин.
Нагрузка СМО ρ = λ/ μ = 0,5/0,4 = 1,25
Нагрузка на один канал Ψ = ρ/n = 1,25/2 = 0,625
Вероятность простоя СМО
p0= [1+(2/1!)*0,625+ (2^2/2!)*0,625^2+(2^2/2!)*0,625^3*(1 - 0,625^3)/(1-0,625)] ^(-1)= 0,249
Вероятность отказа
pr = p5 = (2^2/2!)* 0,625^(2+3)*0,249 = 0,048
Относительная пропускная способность
Q = 1 - 0,048= 0,952
Слайд 40Абсолютная пропускная способность
A= λ*Q= 0,5*0,952= 0,476 клиент/мин.
Среднее число занятых операторов
Среднее
число клиентов в очереди:
Среднее число клиентов в системе:
Слайд 41Среднее время обслуживания клиента:
Среднее время пребывания клиента в очереди:
Среднее время
пребывания клиента в пункте обмена:
Слайд 426.Одноканальная СМО с ожиданием и ограниченной очередью.
n=1 ψ = ρ
Вероятность
отказа в обслуживании
Вероятность принятия заявки
Слайд 43Относительная пропускная способность:
Абсолютная пропускная способность:
Предельные вероятности состояний:
Среднее число заявок в
очереди:
Слайд 44Среднее число заявок в очереди:
Среднее время ожидания в очереди:
Среднее время
пребывания в системе:
Слайд 457. Многоканальная СМО с ожиданием и неограниченной очередью
Решение системы уравнений:
Нормировочное
условие:
Слайд 46 Вероятность отказа:
Вероятность принятия заявки:
Абсолютная пропускная способность:
Среднее число
занятых каналов:
Среднее число заявок
в очереди:
Слайд 47Среднее время ожидания в очереди:
Среднее число заявок, находящихся в системе:
Среднее
время пребывания заявок в системе:
Слайд 48Пример. В кассе метрополитена, продающей карточки на проезд, работают два
окна. В среднем один кассир тратит на обслуживание одного пассажира
0,5 минуты. В среднем к кассе подходит 3 чел./мин.
Найти основные характеристики работы кассы.
Слайд 49Решение:
Двухканальная СМО с ожиданием и без ограничения на длину очереди.
Число
каналов: n= 2
Интенсивность входного потока заявок: λ = 3 чел./мин.
Интенсивность
потока обслуживания μ = 2 чел./мин.
Нагрузка СМО ρ = λ / μ = 3/2 = 1,5
Нагрузка на один канал Ψ = ρ/n = 1,5/2 = 0,75
Вероятность простоя СМО (оба кассира свободны):
p0=1/ [1+(2/1!)*0,75+ (2^2/2!)*0,75^2+(2^2/2!)*0,75^3/(1-0,75)]= 0,143
Вероятность отказа
pr = 0
Относительная пропускная способность
Q = 1
Слайд 50
Среднее число занятых кассиров:
Среднее число пассажиров в очереди:
Среднее число пассажиров
у касс:
Среднее время пребывания пассажиров в очереди:
Среднее время затрачиваемое пассажиром
на покупку карточки:
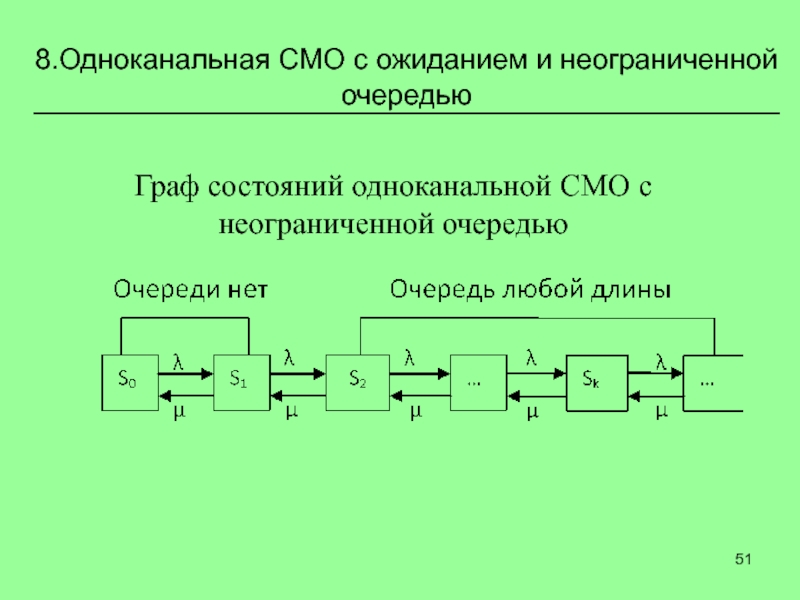
Слайд 51Граф состояний одноканальной СМО с неограниченной очередью
8.Одноканальная СМО с ожиданием
и неограниченной очередью
Слайд 52Приведенная интенсивность нагрузки СМО:
при λ < μ
= λ /μ
Вероятность
обслуживания: pобс = 1
Вероятность отказа: pотк = 0
Вероятность простоя системы:
p0 = 1 - ρ
Вероятность занятости системы: p1 = 1 – p0
Вероятность пребывания в очереди k заявок:
pk = ρk(1- ρ )
Слайд 53Относительная пропускная способность :
Q = pобс = 1
Абсолютная пропускная способность:
A
= λ *Q = λ
Среднее число обслуженных заявок:
Lоб = ρ
Среднее число заявок в очереди:
Среднее число заявок в системе:
LСМО = Lоч + Lоб
Слайд 54Пример. В магазине работает только один продавец. Интенсивность обслуживания составляет
25 чел./час. Простейший поток покупателей поступает с интенсивностью 20 чел./час.
Найти основные характеристики работы СМО.
Слайд 55Интенсивность входного потока:
Интенсивность потока обслуживания:
Приведенная интенсивность нагрузки СМО:
при λ
< μ
= λ /μ = 20/25 = 0,8
Вероятность обслуживания: pобс
= 1
Вероятность отказа: pотк = 0
λ = 20 чел./час
μ = 25 чел./час.
Слайд 56Вероятность простоя продавца: p0 = 1 - ρ =
1
– 0,8 = 0,2
Вероятность занятости продавца: p1 = 1 –
p0
= 1- 0,2 = 0,8
Вероятность пребывания в очереди k заявок:
pk = ρk(1- ρ )
Вероятность пребывания в очереди 3 человек:
p3 = ρ3(1- ρ ) = 0,83(1 - 0,8 ) = 0,102
Слайд 57Относительная пропускная способность :
Q = pобс = 1
Абсолютная пропускная способность:
A
= λ *Q = λ = 20 чел./час
Среднее число обслуженных
покупателей:
Lоб = ρ = 0,8
Среднее число покупателей в очереди:
Среднее число покупателей в магазине:
LСМО = Lоч + Lоб = 3.2 + 0.8 = 4
Слайд 58Среднее время ожидания в очереди:
Среднее время пребывания покупателей в
магазине:
TСМО = Tоч + Tобс = 0,16+ 1/25 = 0.2
час. = 12 мин.