Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы с одной степ свободы
Содержание
- 1. Системы с одной степ свободы
- 2. Обобщённая расчётная модельn = 1mcmcДинамика систем с одной степенью свободы масс
- 3. Динамика систем с одной степенью свободы
- 4. Обобщённая расчётная модельmcmcДинамика систем с одной
- 5. Динамика систем с одной степенью свободы
- 6. Динамика систем с одной степенью свободы
- 7. Решение дифференциального уравнения свободного движения системы с
- 8. Динамика систем с одной степенью свободы
- 9. Динамика систем с одной степенью свободы
- 10. Динамика систем с одной степенью свободы
- 11. Динамика систем с одной степенью свободы
- 12. Динамика систем с одной степенью свободы
- 13. ty(t)ydyny*(t)μ0ydyn = μ* yst,FПереходныйпроцессУстановившиесявынужденные колебания011Резонанс – явление
- 14. Динамика систем с одной степенью свободы
- 15. Динамика систем с одной степенью свободы
- 16. Динамика систем с одной степенью свободы
- 17. Определение усилий, перемещений и напряжений в исходной
- 18. Определение усилий, перемещений и напряжений в исходной
- 19. Определение усилий, перемещений и напряжений в исходной
- 20. Определение усилий, перемещений и напряжений в исходной
- 21. К о н т р о л
- 22. К о н т р о л
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
ДИНАМИКА
СООРУЖЕНИЙ
С
ВГ
ДИНАМИКА СИСТЕМ
С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ МАСС
Строительная
механика.
Часть III
Слайд 3Динамика систем
с одной степенью свободы масс
Предпосылки и рабочие гипотезы
линейной
теории динамических расчётов систем
с конечным числом степеней свободы масс
( в
том числе с n = 1 )Рассматриваются линейно деформируемые системы.
Массы сосредоточенные, элементы системы невесомые.
3. Сопротивление внешней среды и внутреннее трение в системе
учитываются по модели вязкого трения.
4. Исследуется движение системы относительно
её исходного состояния, в качестве которого принимается
состояние равновесия, вызванное статическими воздействиями
( постоянными и временными нединамическими ).
5. Определению подлежат динамические составляющие
напряжённо-деформированного состояния движущейся системы
( перемещения, усилия, напряжения, деформации ).
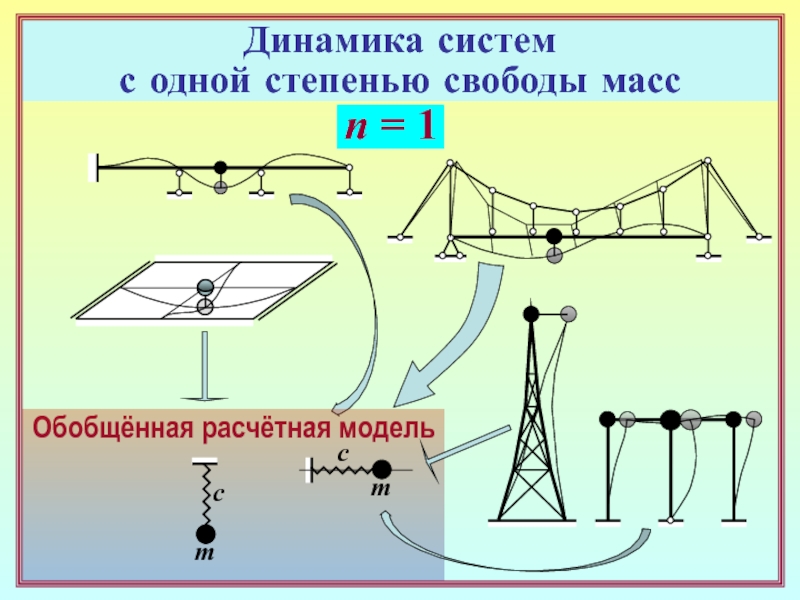
Слайд 4
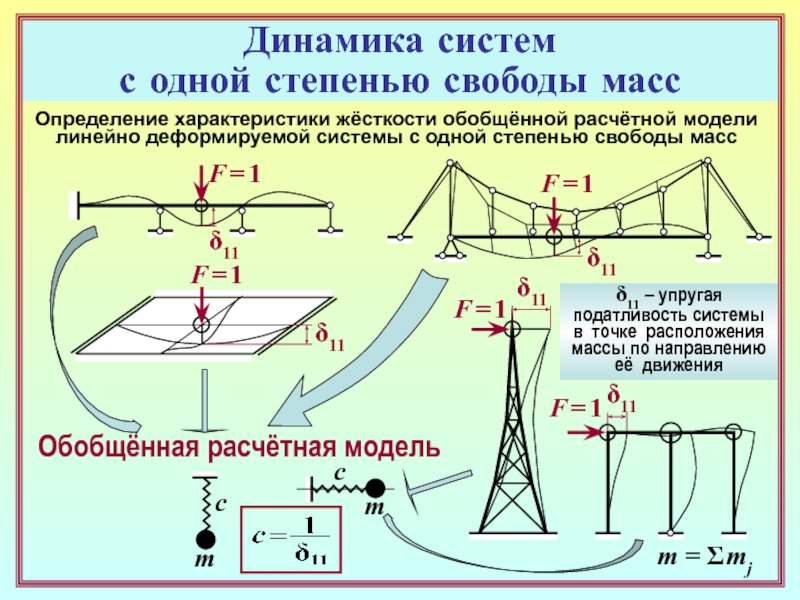
Обобщённая расчётная модель
m
c
m
c
Динамика систем
с одной степенью свободы масс
Определение характеристики
жёсткости обобщённой расчётной модели
линейно деформируемой системы с одной степенью свободы
массF = 1
F = 1
F = 1
F = 1
F = 1
δ11
δ11
δ11
δ11
δ11
m = Σ mj
δ11 – упругая
податливость системы
в точке расположения
массы по направлению
её движения
Слайд 5Динамика систем
с одной степенью свободы масс
Обобщённая
расчётная модель
m
c
Вязкая
среда
Положение
статического
равновесия
( свободное
движение )
m
y(t)
y
0
R(t)
R(t) – реакция
дискретной связи
FD (t)
Сила
сопротивле-
ния (реакция)
вязкой среды
J(t)
– сила инерцииМатематическая
модель
Статическая сторона задачи
( уравнение равновесия )
Σy = 0:
J(t) + FD (t) + R(t) = 0 ( 1 )
Геометрическая сторона задачи
( условие совместности
деформации дискретной связи
и перемещения массы )
Δlc (t) = y(t) ( 2 )
3. Физическая сторона задачи
– закон Гука ( для дискретной упругой связи ):
– закон инерции ( для силы инерции Д’Аламбера ):
– закон вязкого сопротивления ( по модели Фойгта ):
( 3 )
W. Voigt
kf – коэффициент сопротивления
Слайд 6Динамика систем
с одной степенью свободы масс
Обобщённая
расчётная модель
Положение
статического
равновесия
( свободное
движение )
m
y(t)
y
0
R(t)
FD (t)
J(t)
Математическая
модель
Разрешающее уравнение –
дифференциальное уравнение
свободного движения:
или
Коэффициент демпфирования
Слайд 7
Решение дифференциального уравнения
свободного движения системы
с одной степенью свободы
масс
Характеристическое уравнение:
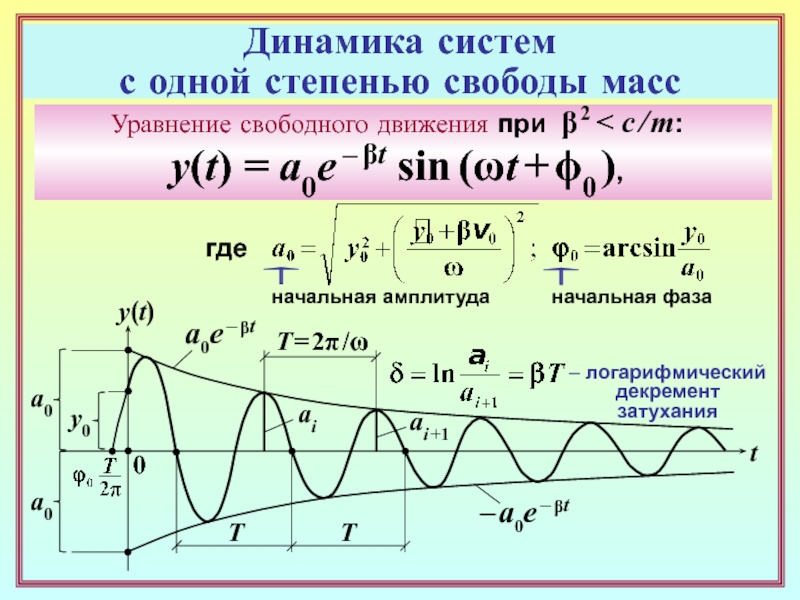
Уравнение свободного движения
при β 2 < c / m:
y(t) = a0e – βt sin (ωt + ϕ0 )
Динамика систем
с одной степенью свободы масс
ω – угловая частота свободных колебаний системы с одной степенью свободы
Слайд 8Динамика систем
с одной степенью свободы масс
Уравнение свободного движения при
β 2 < c / m:
y(t) = a0e – βt
sin (ωt + ϕ0 ), где
а0
а0
y0
y(t)
t
a0e – βt
T
T
аi
ai +1
– логарифмический
декремент
затухания
0
– a0e – βt
T = 2π /ω
начальная амплитуда
начальная фаза
Слайд 9Динамика систем
с одной степенью свободы масс
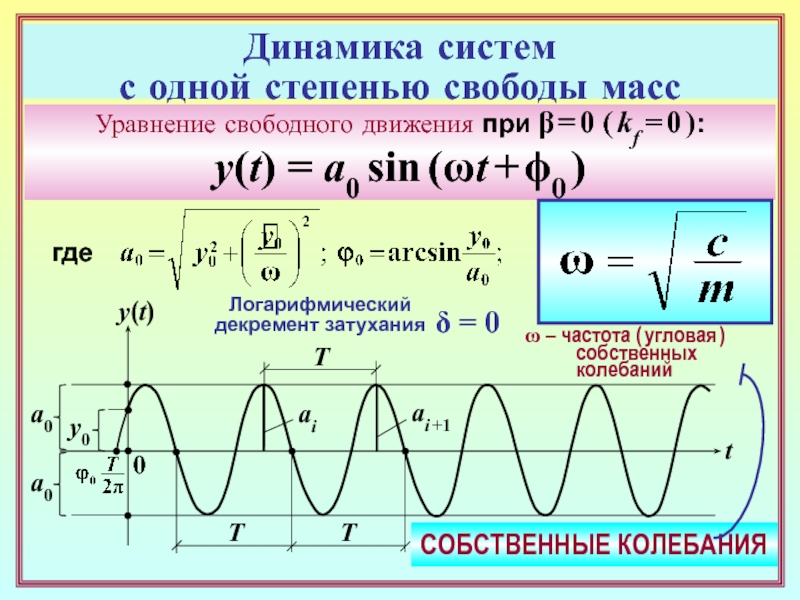
Уравнение свободного движения при
β = 0 ( kf = 0 ):
y(t) = a0
sin (ωt + ϕ0 ) где
а0
а0
y0
y(t)
t
T
T
T
аi
ai +1
Логарифмический
декремент затухания
δ = 0
СОБСТВЕННЫЕ КОЛЕБАНИЯ
0
– частота ( угловая )
собственных
колебаний
Слайд 10Динамика систем
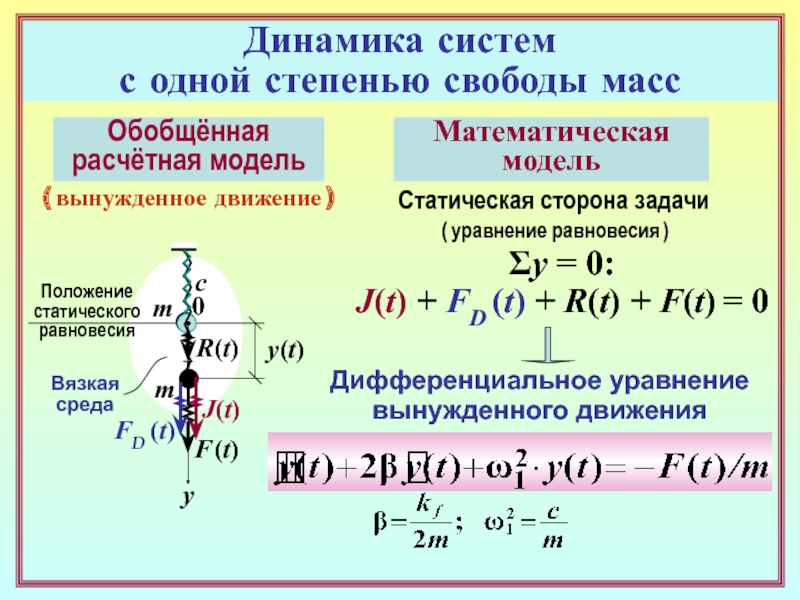
с одной степенью свободы масс
Обобщённая
расчётная модель
m
c
Вязкая
среда
Положение
статического
равновесия
m
y(t)
y
F (t)
(
вынужденное движение )
0
R(t)
FD (t)
J(t)
Математическая
модель
Статическая сторона задачи
( уравнение равновесия )Σy = 0:
J(t) + FD (t) + R(t) + F(t) = 0
Дифференциальное уравнение
вынужденного движения
Слайд 11Динамика систем
с одной степенью свободы масс
a0e – βt sin
(ωt + ϕ0 )
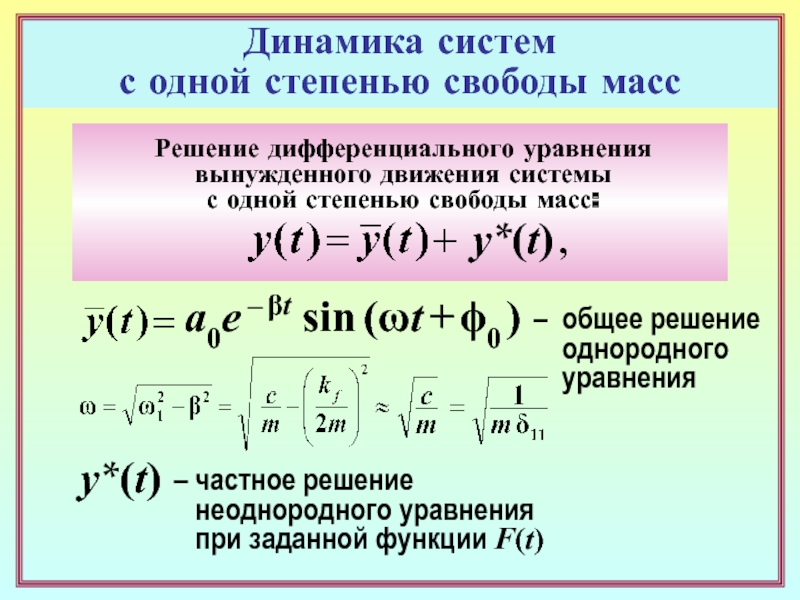
Решение дифференциального уравнения
вынужденного движения системы
с
одной степенью свободы масс: – общее решение
однородного
уравнения
– частное решение
неоднородного уравнения
при заданной функции F(t)
y*(t)
y*(t) ,
Слайд 12Динамика систем
с одной степенью свободы масс
t
F(t)
F
F
y*(t) = μ *
yst,F sin ( ωF t – ε ) =
= ydyn * sin ( ωF t – ε ) ydyn
y*(t)
t
ydyn
TF
TF
Δt
Δt
yst,F = F/c ;
Динамический коэффициент
( коэффициент динамичности )
– коэффициент
неупругого
сопротивления
0
0
Частный случай динамического воздействия – вибрационная нагрузка F(t) = F * sin ωF (t)
γ =
0,025 – сталь
0,05 – дерево
0,08 – кирпичная кладка
0,1 – бетон и железобетон
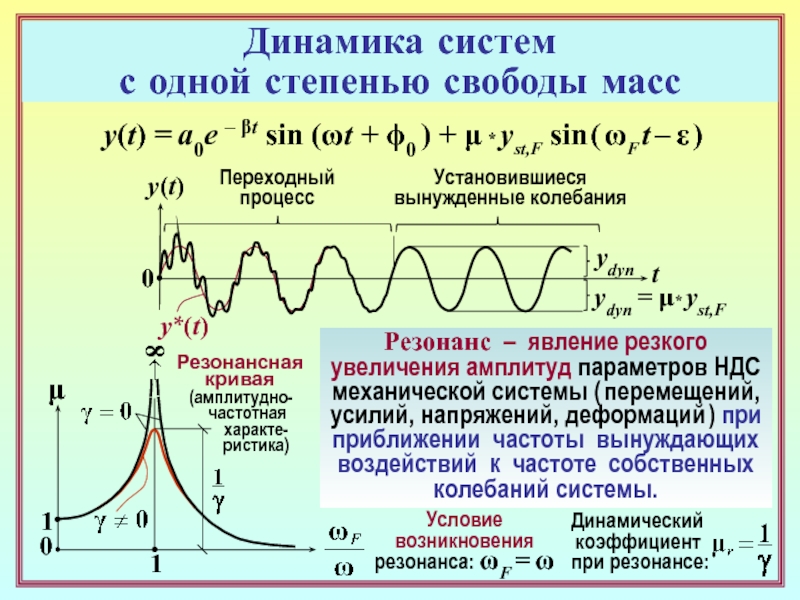
Слайд 13
t
y(t)
ydyn
y*(t)
μ
0
ydyn = μ* yst,F
Переходный
процесс
Установившиеся
вынужденные колебания
0
1
1
Резонанс – явление резкого
увеличения амплитуд параметров
НДС механической системы ( перемещений, усилий, напряжений, деформаций ) при
приближении частоты вынуждающих воздействий к частоте собственныхколебаний системы.
Динамика систем
с одной степенью свободы масс
y(t) = a0e – βt sin (ωt + ϕ0 ) + μ * yst,F sin ( ωF t – ε )
Условие
возникновения
резонанса: ωF = ω
Динамический
коэффициент
при резонансе:
8
Резонансная
кривая
(амплитудно-
частотная
характе-
ристика)
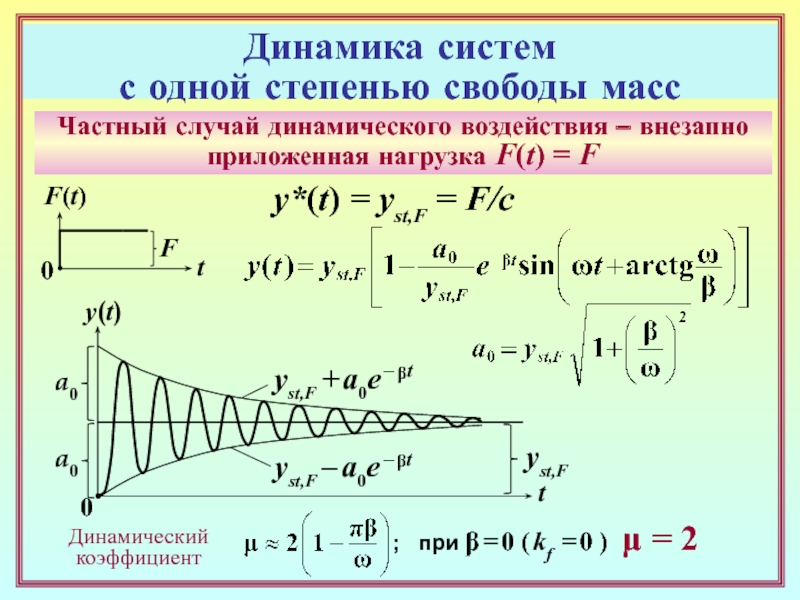
Слайд 14Динамика систем
с одной степенью свободы масс
Частный случай динамического воздействия
– внезапно приложенная нагрузка F(t) = F
0
F(t)
F
t
y*(t) = yst,F =
F/ca0
y(t)
t
yst,F + a0e – βt
a0
0
yst,F – a0e – βt
yst,F
Динамический коэффициент
; при β = 0 ( kf = 0 ) μ = 2
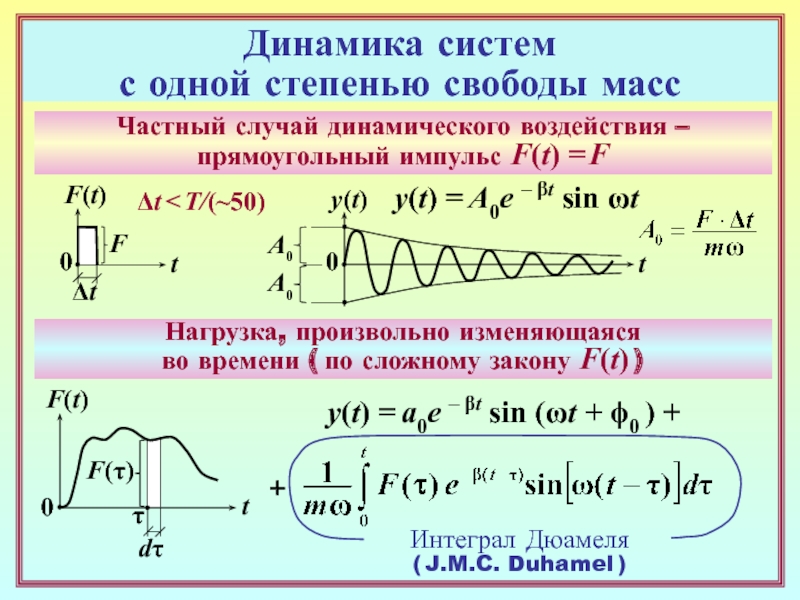
Слайд 15Динамика систем
с одной степенью свободы масс
Частный случай динамического воздействия
–прямоугольный импульс F(t) = F
0
F(t)
F
t
t
0
Интеграл Дюамеля
( J.M.C. Duhamel )
Δt
Нагрузка, произвольно
изменяющаясяво времени ( по сложному закону F(t) )
F(t)
τ
dτ
F(τ)
y(t) = a0e – βt sin (ωt + ϕ0 ) +
+
Δt < T/(~50)
0
t
y(t)
A0
A0
y(t) = A0e – βt sin ωt
Слайд 16Динамика систем
с одной степенью свободы масс
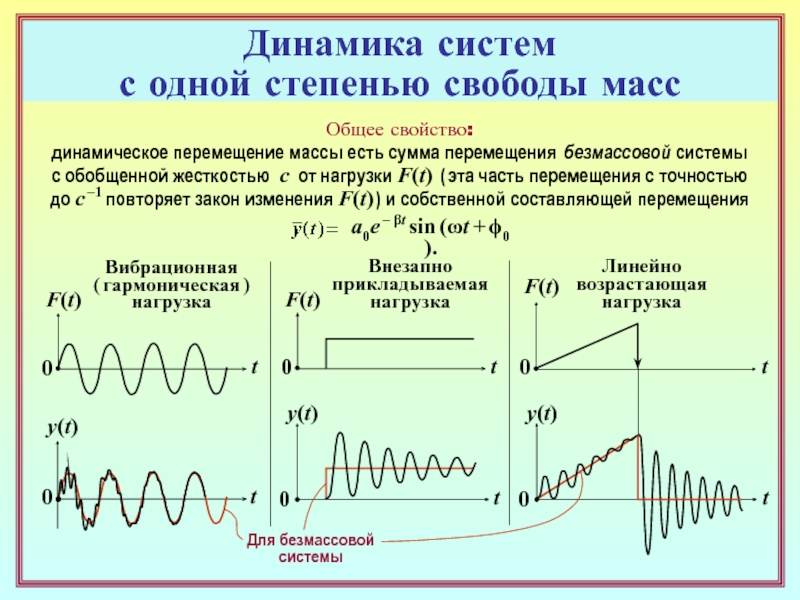
Общее свойство:
динамическое перемещение
массы есть сумма перемещения безмассовой системы
с обобщенной жесткостью c
от нагрузки F(t) ( эта часть перемещения с точностью до c –1 повторяет закон изменения F(t) ) и собственной составляющей перемещения
t
0
F(t)
0
t
y(t)
a0e – βt sin (ωt + ϕ0 ).
t
0
y(t)
t
0
F(t)
t
F(t)
0
0
t
y(t)
Вибрационная
( гармоническая )
нагрузка
Внезапно
прикладываемая
нагрузка
Линейно
возрастающая
нагрузка
Для безмассовой
системы
Слайд 17
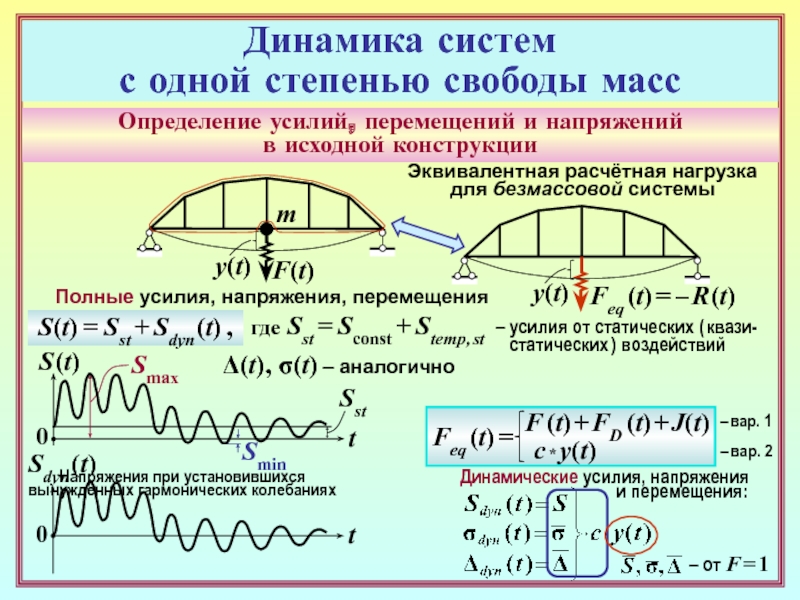
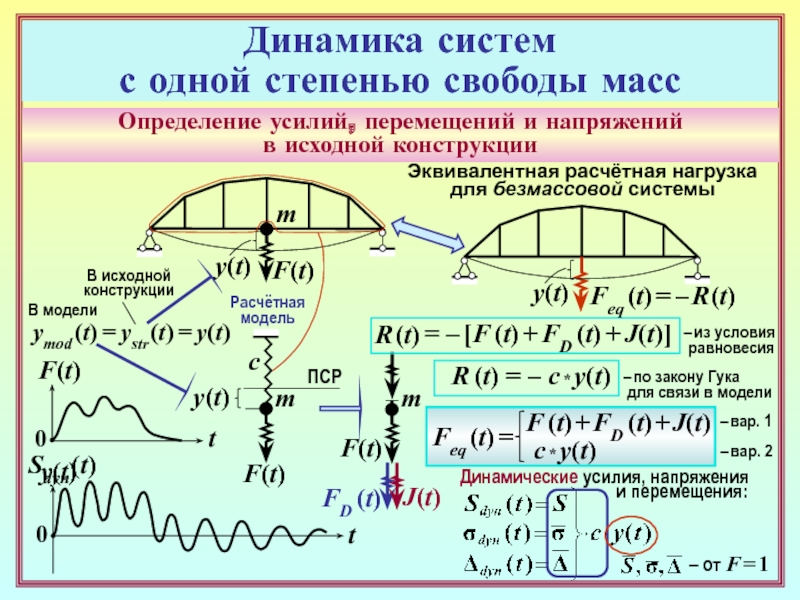
Определение усилий, перемещений и напряжений
в исходной конструкции
F(t)
t
0
F(t)
0
t
y(t)
y(t)
m
c
m
F(t)
ПСР
y(t)
ymod (t)
= ystr (t) = y(t)
F(t)
m
R (t)
FD (t)
J(t)
= – [F
(t) + FD (t) + J(t)]R (t) = – с * y(t)
Эквивалентная расчётная нагрузка
для безмассовой системы
y(t)
Feq (t) = – R (t)
Feq (t) =
F (t) + FD (t) + J(t)
с * y(t)
– вар. 1
– вар. 2
Динамические усилия, напряжения
и перемещения:
– от F = 1
– из условия
равновесия
– по закону Гука
для связи в модели
Расчётная
модель
Динамика систем
с одной степенью свободы масс
Sdyn (t)
В модели
В исходной
конструкции
Слайд 18
Определение усилий, перемещений и напряжений
в исходной конструкции
F(t)
0
t
y(t)
m
R (t)
= –
[F (t) + FD (t) + J(t)]
R (t) = –
с * y(t)Эквивалентная расчётная нагрузка
для безмассовой системы
y(t)
Feq (t) = – R (t)
Feq (t) =
F (t) + FD (t) + J(t)
с * y(t)
– вар. 1
– вар. 2
Динамические усилия, напряжения
и перемещения:
– от F = 1
– из условия
равновесия
– по закону Гука
для связи в модели
Динамика систем
с одной степенью свободы масс
Sdyn (t)
Полные усилия, напряжения, перемещения
Слайд 19
Определение усилий, перемещений и напряжений
в исходной конструкции
F(t)
0
t
y(t)
m
Эквивалентная расчётная нагрузка
для
безмассовой системы
y(t)
Feq (t) = – R (t)
Feq (t) =
F (t)
+ FD (t) + J(t)с * y(t)
– вар. 1
– вар. 2
Динамические усилия, напряжения
и перемещения:
– от F = 1
Динамика систем
с одной степенью свободы масс
Sdyn (t)
S(t) = Sst + Sdyn (t) ,
где Sst = Sconst + Stemp, st
0
t
S (t)
Smax
Smin
Sst
Полные усилия, напряжения, перемещения
Δ(t), σ(t) – аналогично
Напряжения при установившихся
вынужденных гармонических колебаниях
– усилия от статических ( квази-
статических ) воздействий
Слайд 20
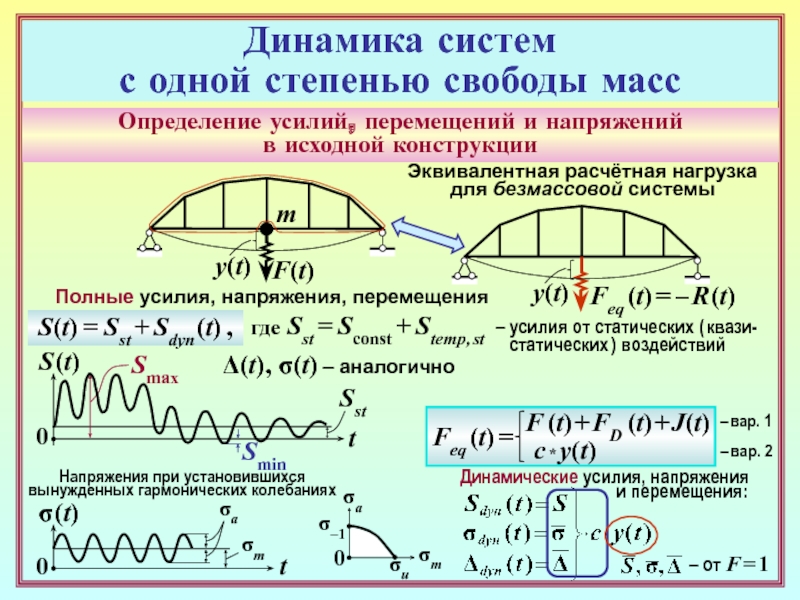
Определение усилий, перемещений и напряжений
в исходной конструкции
F(t)
0
t
y(t)
m
Эквивалентная расчётная нагрузка
для
безмассовой системы
y(t)
Feq (t) = – R (t)
Feq (t) =
F (t)
+ FD (t) + J(t)с * y(t)
– вар. 1
– вар. 2
Динамические усилия, напряжения
и перемещения:
– от F = 1
Динамика систем
с одной степенью свободы масс
σ (t)
S(t) = Sst + Sdyn (t) ,
где Sst = Sconst + Stemp, st
0
t
S (t)
Smin
Sst
Напряжения при установившихся
вынужденных гармонических колебаниях
σm
σa
σm
σa
0
σu
σ–1
Δ(t), σ(t) – аналогично
Полные усилия, напряжения, перемещения
Smax
– усилия от статических ( квази-
статических ) воздействий
Слайд 21К о н т р о л ь н ы
е в о п р о с ы
( в
скобках даны номера слайдов, на которых можно найти ответы на вопросы;для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 21» )
1. Перечислить предпосылки и рабочие гипотезы линейной теории динамических
расчётов систем с конечным числом степеней свободы масс. ( 3 )
2. Может ли число степеней свободы масс n быть равным 1, если в системе имеется
несколько сосредоточенных масс? ( 2 )
3. Если в системе есть только одна сосредоточенная масса, то обязательно ли n = 1 ?
4. Какова обобщённая расчётная модель системы с одной степенью свободы масс? ( 2 )
5. Как определяется характеристика с жёсткости обобщённой расчётной модели
для любой линейно деформируемой системы с одной степенью свободы масс? ( 4 )
6. Какие уравнения описывают состояние расчётной модели при решении задач
динамики системы с n = 1 кинетостатическим методом? ( 5 )
7. Какие силы учитываются в уравнении равновесия? ( 5 )
8. Каково условие совместности перемещений и деформаций элементов расчётной
модели? ( 5 )
9. Какие физические зависимости используются в решении динамической задачи? ( 5 )
10. Как получается дифференциальное уравнение свободного движения массы системы
с n = 1 ? ( 6 ) Каково его решение (функция, описывающая перемещение массы)? ( 7 )
11. Какими компонентами выражения y(t) описывается колебательный характер
свободного движения и затухание процесса? ( 8 )
12. Из-за чего происходит затухание свободных колебаний?
13. От чего зависит частота свободных колебаний? ( 7 )
14. Какие параметры функции y(t) зависят от собственных свойств системы,
а какие – от начальных условий свободного движения? ( 7, 8 )
15. Каков закон изменения перемещения массы в свободном движении системы с n = 1
при отсутствии сопротивления? ( 9 ) По какой формуле в этом случае определяется
частота собственных колебаний? ( 9 )
*) Только в режиме «Показ слайдов»
Слайд 22К о н т р о л ь н ы
е в о п р о с ы
( в
скобках даны номера слайдов, на которых можно найти ответы на вопросы;для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 22» )
16. Чем отличаются уравнения кинетостатического метода в случае вынужденного движе-
ния системы с одной степенью свободы масс от уравнений свободного движения? ( 10 )
17. Каков вид выражения динамического перемещения y(t) массы в общем случае
вынужденного движения? ( 11 ) Как в нём учитывается характер заданной
динамической нагрузки? ( 11 )
18. Какая функция y(t) описывает динамическое перемещение массы при действии
гармонической ( вибрационной ) нагрузки? ( 12 )
19. От чего зависит разность фаз гармонической нагрузки и вызываемого ею
динамического перемещения массы ? ( 12 )
20. Что такое динамический коэффициент ( коэффициент динамичности )? ( 12 )
21. По какой формуле вычисляется динамический коэффициент при гармонической
нагрузке? ( 12 )
21. Что понимается под переходным процессом в случае колебаний от вибрационной
нагрузки? ( 13 )
22. Что такое установившиеся вынужденные колебания при вибрационной нагрузке? ( 13 )
По какому закону и с какой частотой они происходят? ( 13 )
23. Что представляет собой резонанс и при каких условиях он возникает? ( 13 )
24. Чему равен динамический коэффициент при резонансе? ( 13 )
25. Каков характер движения массы при внезапном приложении нагрузки? ( 14 )
Чему равен динамический коэффициент при таком воздействии? ( 14 )
26. Какое общее свойство динамического перемещения массы системы с одной степенью
свободы можно использовать для предсказания вида функции y(t) ? ( 16 )
27. Как по найденной функции y(t) динамического перемещения массы обобщённой
расчётной модели определяются динамические и полные усилия, напряжения
и напряжения в исходной конструкции? ( 17 – 20 )
28. Как проверяется прочность материала при циклических напряжениях? ( 20 )
*) Только в режиме «Показ слайдов»






![Системы с одной степ свободы Определение усилий, перемещений и напряжений в исходной конструкцииF(t)0ty(t)mR (t)= – [F Определение усилий, перемещений и напряжений в исходной конструкцииF(t)0ty(t)mR (t)= – [F (t) + FD (t) + J(t)]R](/img/thumbs/fc31b29d0f3bf062a7c4190d0984663e-800x.jpg)