позиционные и непозиционные
Непозиционная система счисления – это система, где
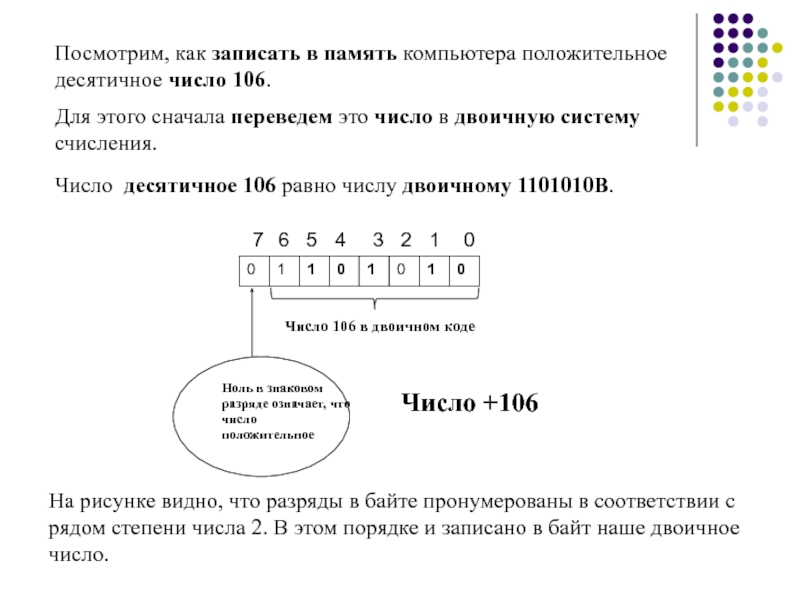
порядок цифры в числе определяется по установленному правилу. Например, непозиционной системой счисления является «римская» система.Позиционной системой счисления, называется система - где порядок цифры в числе определяется рядом степени числа, которое является основанием данной системы счисления.
Система счисления - это совокупность правил наименования и изображения чисел с помощью набора знаков.