Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сопротивление грунтов сдвигу. Закон Кулона (Кулона – Мора )
Содержание
- 1. Сопротивление грунтов сдвигу. Закон Кулона (Кулона – Мора )
- 2. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫДалматов Б.И. Механика грунтов, основания
- 3. Физический смысл прочностных характеристик:Удельное сцепление с –
- 4. Скальные грунты, как и многие упругие тела,
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Рис. Схема потери устойчивости откосаПри потере устойчивости происходит
- 13. Под действием внешней нагрузки в
- 14. Таким образом, в основании фундаментов при достижении предельной
- 15. Слайд 15
- 16. Сопротивление грунтов сдвигуНормальные и касательные напряжения на
- 17. Сопротивление грунтов сдвигуСхема прибора одноплоскостного сдвига или среза
- 18. Слайд 18
- 19. Еще в 18 веке французским ученым Ш. Кулоном было
- 20. НАПРЯЖЕННОЕ СОСТОЯНИЕ ГРУНТАЕсли к поверхности грунта основания
- 21. Структурные связи (кристаллизационные ионно-коллоидные) зависят от геоморфологических особенностей
- 22. НАПРЯЖЕННОЕ СОСТОЯНИЕ ГРУНТАПолные напряжения по граням элемента σ' и σ" можно разложить на нормальные составляющие σz и σx и касательные (сдвигающие) τ (рис. 2,а)
- 23. Нормальные напряжения сжимают элемент, а касательные "перекашивают"
- 24. ВНУТРЕННЕЕ СОПРОТИВЛЕНИЕ ГРУНТА СДВИГУВнутреннее сопротивление грунта сдвигу
- 25. ВНУТРЕННЕЕ СОПРОТИВЛЕНИЕ ГРУНТА СДВИГУ2. Силы сцепления. Характеризуют сопротивление
- 26. Слайд 26
- 27. Теория Кулона Кулон полагал, что разрушение материала начинается
- 28. Если образец песка 1 поместить в сдвиговой
- 29. Если мы
- 30. Слайд 30
- 31. Слайд 31
- 32. СОПРОТИВЛЕНИЕ СДВИГУ СВЯЗНЫХ ГРУНТОВГлины, суглинки и супеси
- 33. Навье видоизменил теорию Кулона, приняв, что сопротивление
- 34. Подставляя эти значения в уравнение Кулона –
- 35. Существуют разнообразные сдвиговые приборы, применяемые в лабораторных
- 36. Рис. 2.11. Схема четырехлопастной
- 37. Общее напряженное состояние грунта
- 38. Напряжённое состояние в точке грунта по теории
- 39. Круги Мора, касающиеся предельной кривой,
- 40. 3. ОСОБЕННОСТИ ТЕОРИИ ПРОЧНОСТИ КУЛОНА-МОРАМор принял, что
- 41. 3. ОСОБЕННОСТИ ТЕОРИИ ПРОЧНОСТИ КУЛОНА-МОРА Теория прочности Мора
- 42. 4. Прямолинейные огибающие Простейшими огибающими предельных кругов Мора
- 43. Обозначив tg φ через f, приходим к
- 44. Из рис. следует, что при плоском напряженном
- 45. Опыты показывают, что для одних грунтов влиянием
- 46. Пользуясь свойствами полюса крута Мора, можно найти
- 47. Спасибо за внимание!
- 48. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Сопротивление грунтов сдвигу. Закон Кулона (Кулона – Мора)
Новосибирский государственный
архитектурно-строительный
университет
Слайд 2СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Далматов Б.И. Механика грунтов, основания и фундаменты. –
М.: Стройиздат, 1988.
Проектирование фундаментов зданий и подземных сооружений: Учеб. пособие/
Под ред. Б.И. Далматова; 2-е изд. – М.: Изд-во АСВ; СПб.: СПбГАСУ, 2001. Цытович Н.А. Механика грунтов (краткий курс): Учебник для строит. вузов. – М.: Высш. шк., 1983.
Бартоломей А.А. Механика грунтов: Учеб. издание/ АСВ, Москва, 2004;
Малышев М.В., Болдырев Г.Г. Механика грунтов. Основания и фундаменты (в вопросах и ответах) / Учебное пособие. – М.: Издательство Ассоциации строительных вузов, 2004;
Тер-Мартиросян З.Г. Механика грунтов/ Учебное пособие. – М.: Издательство Ассоциации строительных вузов, 2005;
Слайд 3Физический смысл прочностных характеристик:
Удельное сцепление с – это сопротивление грунта
срезу (сдвигу) при отсутствии нормальных
напряжений σ на площадке
сдвига (среза).Угол внутреннего трения φ равен углу наибольшего отклонения полного давления q от нормали к площадке, на которой оно действует.
При отклонении q на угол φ, равный углу θmax наступает состояние предельного равновесия грунта.
Слайд 4Скальные грунты, как и многие упругие тела, разрушаются от растяжения,
сжатия, кручения, изгиба и комбинаций этих воздействий. Разрушения оценивают соответствующими
расчётными сопротивлениями этих видов воздействий.Нескальные грунты разрушаются только сдвигом одной части относительно другой.
Основные показатели грунтов, используемые при расчётах предельной прочности и устойчивости грунтов, а также при расчете давления грунтов на ограждения могут быть получены в результате изучения сопротивляемости грунта сдвигу, обусловленной:
в сыпучих телах – внутренним трением,
в связных грунтах – трением и сцеплением.
Слайд 12Рис. Схема потери устойчивости откоса
При потере устойчивости происходит сдвиг одной части относительно
другой.
Сопротивление грунтов сдвигу
Сопротивление грунтов сдвигу является их важнейшим прочностным свойством,
знание которого необходимо для решения разных задач механики грунтов.Слайд 13 Под действием внешней нагрузки в определенных зонах грунта
связи между частицами разрушаются и происходит смещение (сдвиг) одних частиц
относительно других — грунт приобретает способность неограниченно деформироваться под данной нагрузкой. Разрушение массива грунта происходит в виде перемещения одной части массива относительно другой (оползание откоса, выпор грунта из-под сооружения и т. п.).Определение сопротивления грунта сдвигу, производимое в лаборатории или полевых условиях, моделирует разрушение грунта в сооружении и заключается в измерении усилия, необходимого для сдвига образца или некоторого объема грунта, находящегося под действием известного нормального давления.
Сопротивление грунтов сдвигу
Слайд 14Таким образом,
в основании фундаментов при достижении предельной
нагрузки возникают области
с максимальными
касательными напряжениями, образующие
сплошную поверхность скольжения.
В этот момент происходит
потеря устойчивостиоснования, сопровождающаяся просадкой фундамента.
Поэтому
понятие прочности грунта, его прочностные свойства
напрямую связаны с сопротивлением грунта сдвигу.
Сопротивление грунтов сдвигу
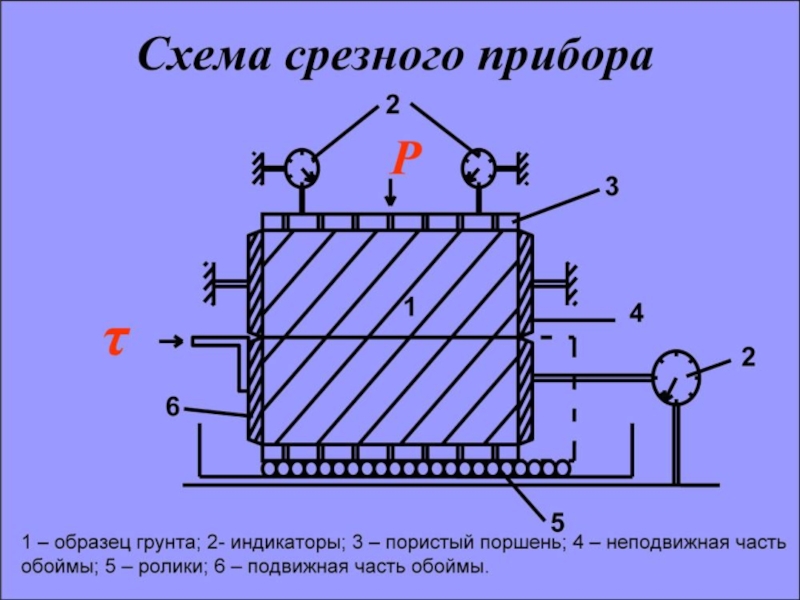
Слайд 16Сопротивление грунтов сдвигу
Нормальные и касательные напряжения на площадке сдвига определяются
в приборе одноплоскостного сдвига или среза.
Уплотнители и прибор одноплоскостного среза
системы «Гидропроект»Слайд 19Еще в 18 веке французским ученым Ш. Кулоном было показано, что сопротивление дисперсной
среды сдвигу обеспечивается:
∙ трением между частицами грунта;
∙ структурными связями между
частицами грунта.Трение между частицами грунта зависит от ряда факторов, среди которых можно выделить:
- минеральный и гранулометрический состав грунт;
- влажность грунта;
- окатанность зерен грунта.
Из курса физики также известно, что сила трения между твердыми телами (в данном случае между частицами грунта) зависит от величины нормальной силы прижимающей эти тела друг другу.
Сопротивление грунтов сдвигу
Слайд 20НАПРЯЖЕННОЕ СОСТОЯНИЕ ГРУНТА
Если к поверхности грунта основания приложить нагрузку p,
в нём возникнет напряженное состояние:
Схема работы призмы грунта с формированием
поверхности скольжения (площадок сдвига) в момент предельного состояния.Слайд 21Структурные связи (кристаллизационные ионно-коллоидные) зависят от геоморфологических особенностей грунта, грансостава, наличия и
толщины пленки связанной воды. Структурные связи и силы зацепления в сумме
образуют силы сцепления между частицами грунта, играющие огромную роль в формировании его прочностных свойств.НАПРЯЖЕННОЕ СОСТОЯНИЕ ГРУНТА
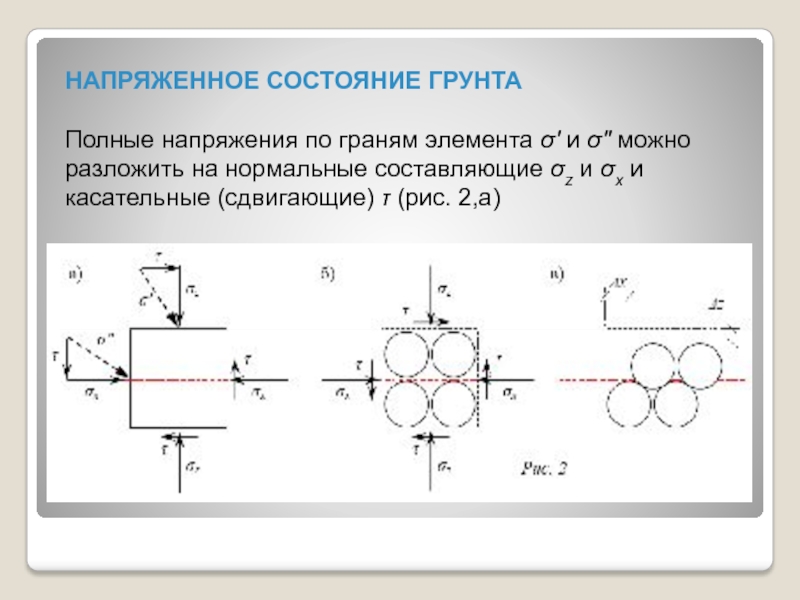
Слайд 22НАПРЯЖЕННОЕ СОСТОЯНИЕ ГРУНТА
Полные напряжения по граням элемента σ' и σ" можно разложить на нормальные
составляющие σz и σx и касательные (сдвигающие) τ (рис. 2,а)
Слайд 23Нормальные напряжения сжимают элемент, а касательные "перекашивают" (поворачивают) его. Если
представить, что элемент состоит из шаровых зёрен грунта, связанных в
точках контакта, то нормальные напряжения сжимают зёрна и усиливают связи между ними, а касательные стремятся вызвать относительный сдвиг зёрен, т.е. разрушить грунт.В том случае, когда касательные усилия превзойдут сопротивление зёрен в точках контакта, произойдет относительный сдвиг частиц (Δx и Δz на рис 2,в). Эти деформации являются необратимыми и свидетельствуют о разрушении грунта в данной точке. Причиной разрушения являются касательные напряжения τ, которые превзошли величину внутреннего сопротивления грунта сдвигу.
НАПРЯЖЕННОЕ СОСТОЯНИЕ ГРУНТА
Слайд 24ВНУТРЕННЕЕ СОПРОТИВЛЕНИЕ ГРУНТА СДВИГУ
Внутреннее сопротивление грунта сдвигу происходит в результате
действия сил трения между частицами и сцепления между ними:
1. Силы трения. Характеризуют
внутреннее сопротивление в идеально сыпучих телах (чистые пески). Трение возникает в точках контакта частиц и зависит от многих факторов, среди которых основными являются:
- минеральный состав грунта;
- величина зёрен грунта;
- форма зёрен (окатанная, пластинчатая, игольчатая);
- состояние поверхности (округлая, угловатая);
- плотность грунта, степень водонасыщенности и др.
Показатель, характеризующий внутреннее трение в грунтах – это угол внутреннего трения (обозначается символом φ , измеряется в градусах).Слайд 25ВНУТРЕННЕЕ СОПРОТИВЛЕНИЕ ГРУНТА СДВИГУ
2. Силы сцепления. Характеризуют сопротивление структурных связей всякому
перемещению связываемых ими частиц, независимо от величины внешнего давления. Сцепление
(связность) в грунте определяется: - наличием капиллярного давления в грунте; - силами молекулярного притяжения между частицами грунта; - наличием в грунте вяжущих веществ (известь, минеральные смолы, соли). Показатель, характеризующий сцепление в грунтах – удельное сцепление (обозначается символом c , измеряется в паскалях). Каким образом определить внутреннее сопротивление грунта сдвигу, характеризуемое показателями φ и c?Слайд 27Теория Кулона
Кулон полагал, что разрушение материала начинается в точке, в
которой наибольшие касательные напряжения достигают некоторого предельного значением прочности данного
материала при сдвиге. Максимальное касательное напряжение τмакс действует в плоскости, нормаль к которой делит угол между σ1 и σ111 пополам (рис. 1, а). При одноосном сжатии (σ1 = σ111 = 0), когда σ1 = σR (где σR – предельное значение σ1 соответствующее разрушению), получается, что площадки сдвига наклонены к σ1 под углом в 45°. Однако у большинства материалов этот угол оказывается меньше 45°.Слайд 28Если образец песка 1 поместить в сдвиговой прибор в виде
кольца, разрезанного по горизонтальной плоскости ,(рис. 2.9, а), то, приложив
силу N и постепенно увеличивая силу Т, можно достигнуть среза (сдвига) одной части образца по другой приблизительно по линии, обозначенной пунктиром. Прибор имеет нижнюю неподвижную обойму 4; верхнюю подвижную обойму 3 и зубчатые фильтрующие пластины сверху и снизу 2.Рис. Схема прибора для испытания грунта на сдвиг (о) и графики
сопротивления сдвигу сыпучего (б) и связного (в) грунта
Сопротивление грунтов сдвигу
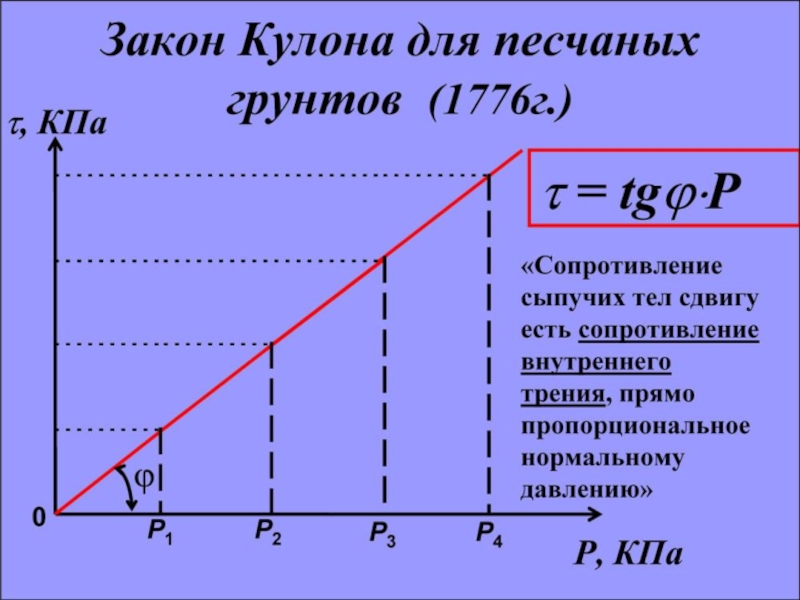
Слайд 29 Если мы проведем несколько таких
опытов при различном вертикальном напряжении σ = N/A (где А
— площадь образца в плоскости среза), то получим, что чем больше σ, тем больше предельное сопротивление грунта сдвигу τu. По данным экспериментов построим зависимость предельного сопротивления сыпучего грунта сдвигу τu от давления (рис. 2.9,б). На основе многочисленных опытов установлено следующее: для несвязных (идеально сыпучих) грунтов экспериментальные точки в пределах обычных изменений напряжений (до 0,5 МПа) оказываются на прямой, выходящей из начала координат. В таком случае для любого нормального напряжения τui = σi tg φ где tg φ — коэффициент внутреннего трения, характеризующий трение грунта о грунт: tg φ = f; φ — угол внутреннего трения. Зависимость установлена Ш. Кулоном еще в 1776 г. Она выражает закон сопротивления сыпучих грунтов сдвигу, который формулируется так:предельное сопротивление сыпучих грунтов сдвигу прямо пропорционально нормальному напряжению. Этот закон называется законом Кулона.
Сопротивление грунтов сдвигу
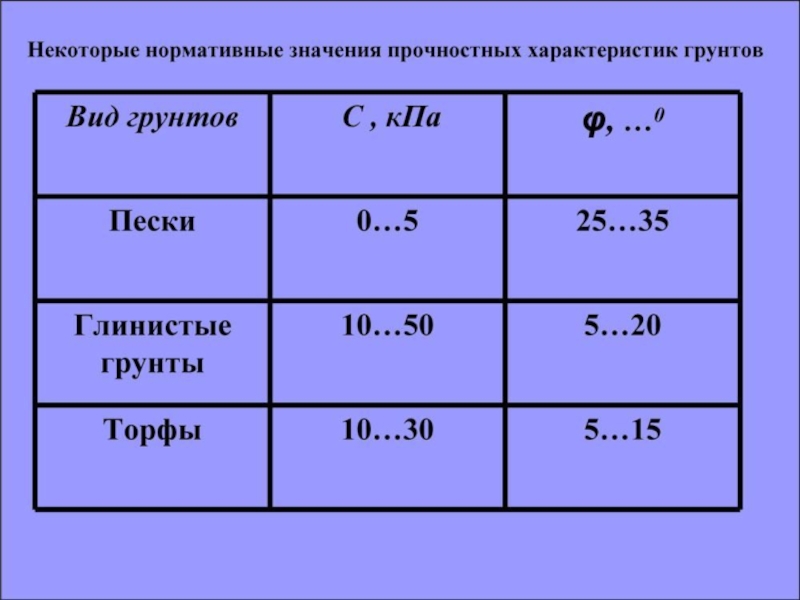
Слайд 32СОПРОТИВЛЕНИЕ СДВИГУ СВЯЗНЫХ ГРУНТОВ
Глины, суглинки и супеси обладают связностью, интенсивность
которой зависит от влажности грунта и степени его уплотнения. Приложенная
к образцу водонасыщенного пылевато-глинистого грунта вертикальная нагрузка сначала передается на поровую воду. Лишь по мере выдавливания воды из пор это давление начинает воздействовать на скелет грунта. В связи с этим образец испытывают сдвиговые воздействия после консолидации грунта, когда все нормальное напряжение уже передано на скелет грунта.Для сохранения природной структуры пылевато-глинистого грунта фильтрующий поршень и днище обычно делают плоским — без зубцов. Если в таком приборе провести несколько испытаний на сдвиг одного и того же грунта, подвергая образцы воздействию различных напряжений σ, получим криволинейную зависимость предельного сопротивления грунта сдвигу τu от σ. Криволинейность зависимости наиболее ощутима при малых значениях σ. При напряжениях в диапазоне 0,05...0,5 МПа практически имеем прямую, описываемую уравнением
Слайд 33Навье видоизменил теорию Кулона, приняв, что сопротивление сдвигу материала при
действии нормального давления возрастает на величину, которая составляет некоторую долю
f от нормального напряжения по площадке. Если нормальное и касательное напряжения по площадке равны σ и τ, то разрушение наступает тогда, когдаτ = с + f σ,
где с – сопротивление материала сдвигу при σ =0.
Слайд 34 Подставляя эти значения в уравнение Кулона – Навье, получим
½ (σ1
+ σ3) sinθ – с + ½ │(σ1 + σ3)
– ½ (σ1 – σ3) cosθ│ f Откуда½ (σ1 + σ3) (sinθ – f cosθ) – ½ f (σ1 + σ3) = с
Следовательно, разрушение наступит, когда левая часть будет равна с. Максимальное значение левая часть будет иметь при
sinθ + f cosθ = max
Беря производную по θ и приравнивая ее нулю, получим
cosθ – f sinθ = 0 откуда
tgθ = 1/ f
Следовательно, разрушение наступит в виде сдвига по той площадке, наклон которой отвечает условию этому условию.
Слайд 35Существуют разнообразные сдвиговые приборы, применяемые в лабораторных испытаниях. На фото
представлены изображения сдвигового прибора АСИЗ, входящего в комплекс автоматизированных систем
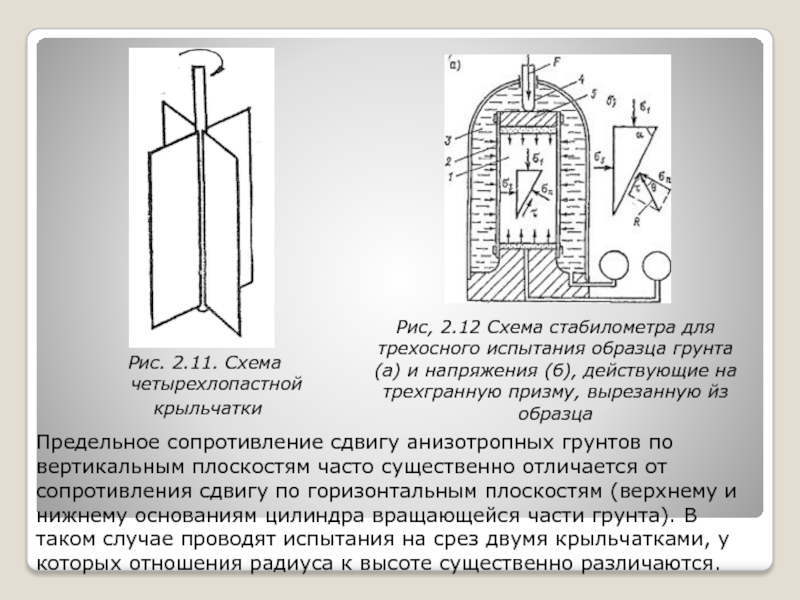
измерения (АСИ).Слайд 36Рис. 2.11. Схема четырехлопастной
крыльчатки
Рис, 2.12 Схема стабилометра для трехосного
испытания образца грунта (а) и напряжения (б), действующие на трехгранную призму, вырезанную йз образцаПредельное сопротивление сдвигу анизотропных грунтов по вертикальным плоскостям часто существенно отличается от сопротивления сдвигу по горизонтальным плоскостям (верхнему и нижнему основаниям цилиндра вращающейся части грунта). В таком случае проводят испытания на срез двумя крыльчатками, у которых отношения радиуса к высоте существенно различаются.
Слайд 37 Общее напряженное состояние грунта можно характеризовать кругом
Мора.
Напряжённое состояние в точке грунта по теории Мора-Кулона: в момент
предельного состояния площадка сдвига наклонена к оси абсцисс на угол αпр.2. ТЕОРИЯ ПРОЧНОСТИ МОРА
Слайд 38Напряжённое состояние в точке грунта по теории Мора-Кулона: в момент
предельного состояния площадка сдвига наклонена к оси абсцисс на угол
αпр.2. ТЕОРИЯ ПРОЧНОСТИ МОРА
Слайд 39 Круги Мора, касающиеся предельной кривой, называются предельными кругами
Мора, а напряженное состояние в точке, характеризуемое предельным кругом Мора
– предельным состоянием. Координаты точки касания дают значения касательного и нормального напряжений в момент разрушения (сдвига) в данной точке, для которой построен круг Мора. С помощью простого построения кругов Мора можно легко найти наклон площадки сдвига. Предельное состояние в точке характеризуется радиусом предельного круга Мора и положением его центра.Так как огибающая имеет две ветви (в положительной и отрицательной полуплоскости), то предельный круг Мора касается огибающей в двух точках, и, следовательно, в каждой точке тела имеются две взаимно наклоненные площадки, по которым одновременно достигается предельное состояние, непосредственно предшествующее разрушению.
2. ТЕОРИЯ ПРОЧНОСТИ МОРА
Слайд 403. ОСОБЕННОСТИ ТЕОРИИ ПРОЧНОСТИ КУЛОНА-МОРА
Мор принял, что сопротивление материала сдвигу
зависит от нормальных напряжений по площадкам сдвига. Чем больше нормальные
напряжения, тем больше это сопротивление. Таким образом, величина касательных напряжений, которые могли бы вызвать сдвиг, будет зависеть от нормальных напряжений по площадкам сдвига, что может быть представлено в видеτ = f(σ)
Теория Кулона – Навье является частным случаем теории Мора.
Если построить круги Мора для момента разрушения некоторого материала при различных напряженных состояниях, как показано на рис. 2, в, г, то уравнение огибающей этих кругов и будет представлять собой искомую функцию f(σ) для данного материала. Эту огибающую обычно называют предельной кривой Мора. Сам Мор в своей работе указывал, что такая кривая должна быть получена экспериментально для каждого материала.
Как показывают опыты, общий вид этих кривых близок к параболе, ординаты которой τR возрастают с увеличением σ, а наклон касательной dτR / dσ с увеличением расстояния от начала координат стремится к нулю.
Слайд 413. ОСОБЕННОСТИ ТЕОРИИ ПРОЧНОСТИ КУЛОНА-МОРА
Теория прочности Мора имеет две особенности.
Первая заключается в том, что абсолютные значения нормального и касательного
напряжений по площадке сами по себе не оказывают влияния на прочность, а решающее значение имеет отношение этих напряжений. В самом деле, т.к. τ = σ tgp; если увеличить пропорционально значения τ и σ, то отношение τ/σ остается без изменений и будет равно тангенсу угла p (отклонения равнодействующей напряжений р от нормали к площадке). Этот угол p называют углом отклонения. Очевидно, что чем больше угол отклонения, тем меньше при том же p величина σ, и больше τ, и тем ближе состояние грунта к моменту разрушения будет. Значение угла p, при которой наступает сдвиг, называется предельным углом отклонения (обычно обозначается φ). Вторая особенность: проекция напряжений, нормальных к плоскости чертежа на эту плоскость, равна нулю. Поэтому эти напряжения не оказывают влияния на величины τ и σ в рассматриваемой плоскости, а следовательно, и не влияют на их отношение.
Слайд 424. Прямолинейные огибающие
Простейшими огибающими предельных кругов Мора являются прямые линии
(рис. 3) с уравнением
τ = с + σi tg φ
Рис. Прямолинейные
огибающие Мора, при наличии сцепленияСлайд 43Обозначив tg φ через f, приходим к условию прочности Кулона
– Навье
τ = f σi + с
Условие разрушения τ
= f(σ) можно заменить в соответствии со сказанным выше эквивалентным условием r =F (σ), так как величина радиуса предельного круга Мора r изменяется в зависимости от абсциссы его центра ОС. Радиус кругаr = (σ1 – σ3)/2, а абсцисса центра ОС = (σ1+σ3)/2
Таким образом, материалу, для которого огибающая предельных кругов Мора вырождается в прямую, отвечают как теория прочности Мора, так и теория прочности Кулона – Навье, которые в этом случае совпадают.
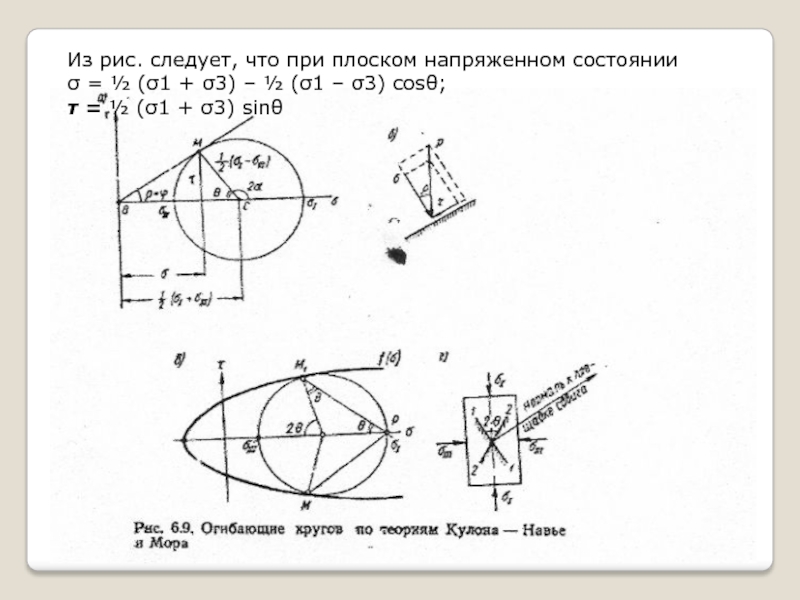
Слайд 44Из рис. следует, что при плоском напряженном состоянии
σ =
½ (σ1 + σ3) – ½ (σ1 – σ3) cosθ;
τ
= ½ (σ1 + σ3) sinθСлайд 45Опыты показывают, что для одних грунтов влиянием третьего главного напряжения
можно пренебрегать в силv его незначительности, для других это надо
учитывать.Если рассматриваемая плоскость является плоскостью главных напряжений, например σ1 и σ3, то на значения τ и σ по площадке сдвига не будет оказывать влияния третье главное напряжение σ2, перпендикулярное плоскости чертежа.
Легко увидеть, что наибольшее значение угол p имеет тогда, когда рассматривается плоскость действия наибольшего и наименьшего главных напряжений. Следовательно, вторая особенность теории Мора заключается в том, что она по самой своей сути не может учесть влияния на прочность третьего главного напряжения, хотя в формулу энергетической теории прочности это напряжение входит.
Слайд 46Пользуясь свойствами полюса крута Мора, можно найти положение площадок сдвига
в разрушающемся теле. Из построения видно, что угол в между
двумя площадками сдвига в точке зависит от напряжений σ1, σ3, так как при их изменении угол о наклона линий MP будет изменяться.У материалов с одинаковым сопротивлением на растяжение и сжатие огибающие кругов Мора превращаются в две параллельные прямые, и углы наклона площадок сдвига к площадкам главных напряжений σ1, σ3 становятся одинаковыми и равными 45°.