Слайд 1
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Кузбасский государственный технический университет имени Т.Ф. Горбачева»
Г.
А. Липина, Г. А. Казунина
Специальные главы математики:
материалы к лекционному курсу
для студентов направления подготовки
140400.62 «Электроэнергетика и электротехника»,
профиль 140404 «Электроснабжение»
Рекомендовано учебно-методической комиссией направления
140400.62 «Электроэнергетика и электротехника»
в качестве учебного пособия
Кемерово 2013
Слайд 2Рецензенты:
Жирнова Т.С. – доцент кафедры математики
Ефременко В.М. – заведующий кафедрой
электроснабжения
Липина Галина Александровна, Казунина Галина Алексеевна
Специальные главы математики
: материалы к лекционному курсу для студентов направления подготовки 140400.62 «Электроэнергетика и электротехника», профиль 140404 «Электроснабжение» очной формы обучения [электронный ресурс] / Г.А. Липина, Г.А. Казунина - электрон. дан.- Кемерово: КузГТУ, 2013. - Систем требования: Pentium IV; 0348 Мб; Windows 97-2003; Microsoft Office Power Point 97- 2003 (CD-ROM дисковод); мышь. Загл.с экрана.
Последовательно, компактно и доступно в форме презентации Microsoft Office Power Point
изложен теоретический материал курса «Специальные главы математики» (3 семестр) согласно государственному образовательному стандарту (ФГОС третьего поколения) и рабочей программе по дисциплине «Специальные главы математики» для направления подготовки 140400.62 «Электроэнергетика и электротехника», профиль 140404 «Электроснабжение». Теоретические положения сопровождаются подробно разобранными задачами и служат основой лекционного курса.
© КузГТУ
© Липина Г.А.
Казунина Г.А

Слайд 3Множества и отображения
Лекция 1
Слайд 4Понятие множества
Множество – одно из основных понятий математики, является первичным
и не имеет строгого определения.
Под множеством понимают объединение объектов, хорошо
различаемых нашей мыслью или интуицией.
Слайд 5Способы задания множеств
Множество считается заданным, если перечислены все его элементы
или указано свойство, которым обладают элементы, принадлежащие данному множеству.
Слайд 6Пустое множество
Если множество не содержит элементов, обладающих характеристическим признаком,
то оно называется пустым.
Пустое множество обозначается ∅.
Слайд 7Изображение множеств
Множества изображают с помощью кругов Эйлера ( диаграмм Венна).
Слайд 10Операции над множествами
К основным операциям над множествами относятся:
1. Пересечение множеств;
2. Объединение множеств;
3. Разность множеств;
4. Дополнение к множеству;
5. Симметрическая разность.
Слайд 16Кортежи и декартово произведение множеств, бинарные отношения, отображения множеств, функции.
Лекция
Слайд 18Равенство кортежей
Два кортежа равны, если:
1. Они имеют одинаковую длину;
2. Их
координаты, стоящие на местах с одинаковыми номерами, равны.
Слайд 19Декартовое произведение множеств
Слайд 21Специальные бинарные отношения
1. Рефлексивное отношение;
2. Симметричное отношение;
3. Транзитивное отношение.
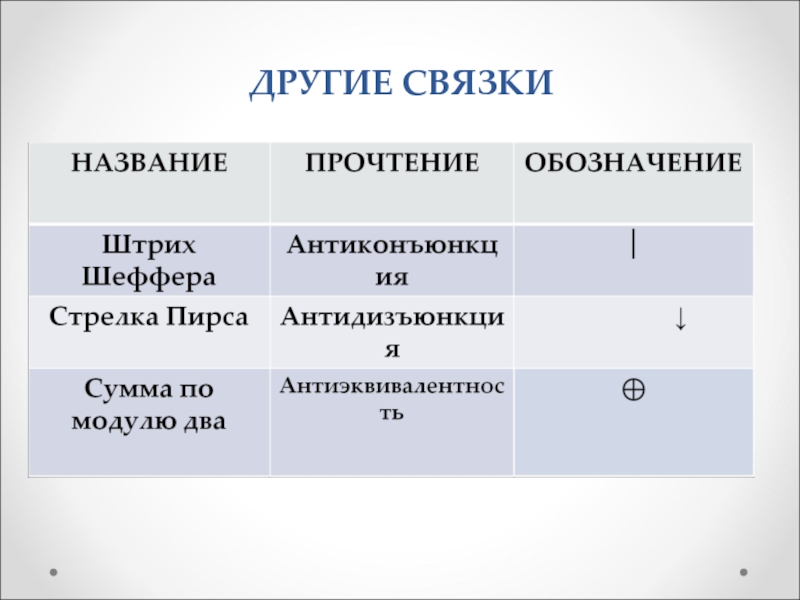
Слайд 26Составные высказывания. Простейшие связки, другие связки.
Лекция 3
Слайд 28Элементарные и составные
высказывания
Составное логическое высказывание – образовано из других
высказываний с помощью логических связок.
Элементарное логическое высказывание – высказывание, не
относящееся к составному.
Слайд 29Логические связки
Логическая связка – любая логическая операция над высказыванием.
Например, употребляемые
в обычной речи слова и словосочетания «не», «и», «или», «
если…,то…», «тогда и только тогда, когда» являются логическими связками.
Слайд 36
1. Отрицание;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения
логических операций используются скобки.
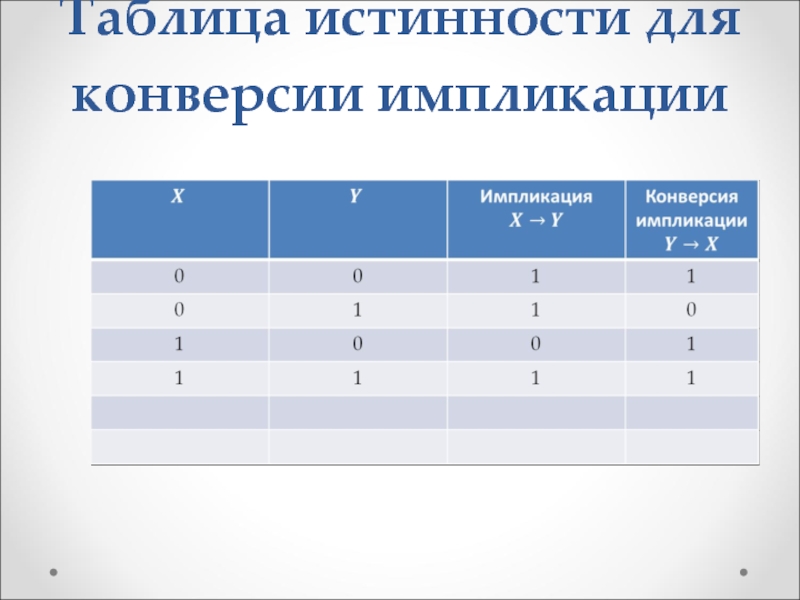
Слайд 43Таблица истинности для конверсии импликации
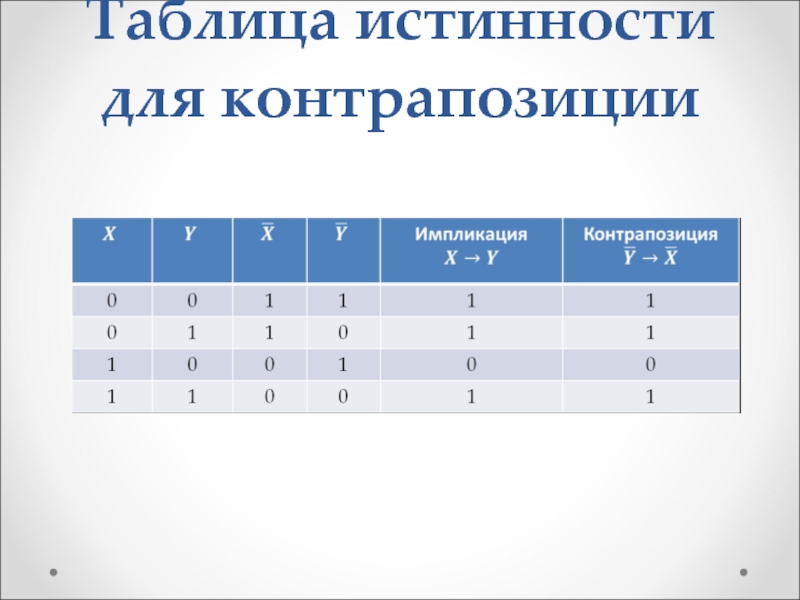
Слайд 44Таблица истинности для контрапозиции
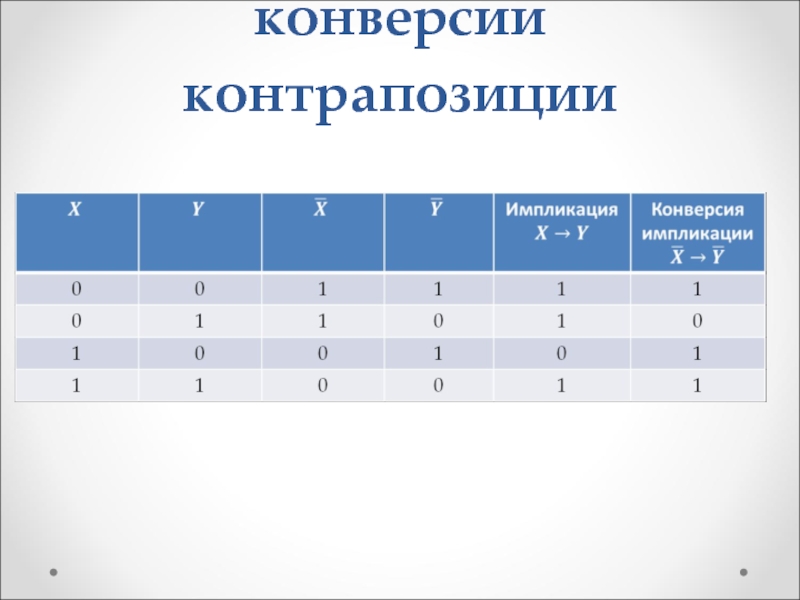
Слайд 45Таблица истинности для конверсии контрапозиции
Слайд 47Основные законы, определяющие свойства логических операций
Слайд 48Основные законы, определяющие свойства логических операций.
Слайд 49Основные законы, определяющие свойства логических операций
Слайд 50Основные законы, определяющие свойства логических операций
Слайд 51Основные законы, определяющие свойства логических операций
Слайд 52Булевы функции.
Свойства элементарных булевых функций
Лекция 5
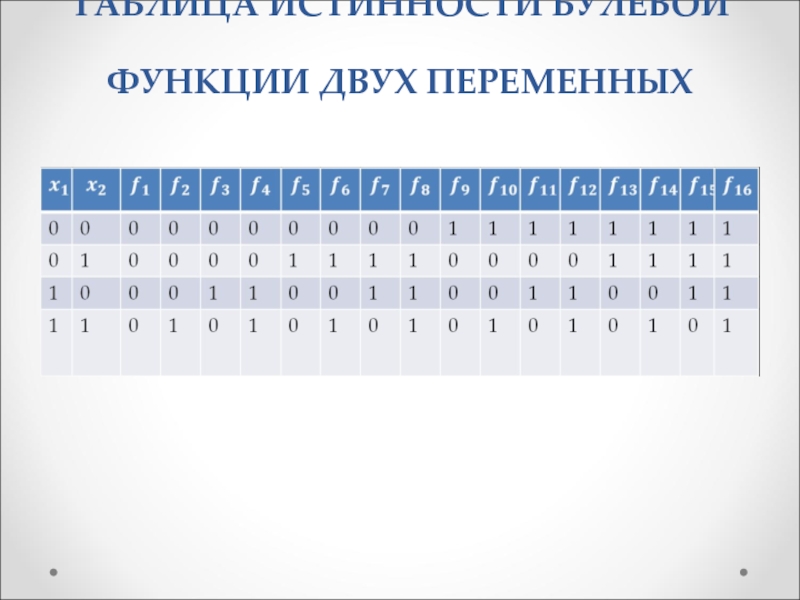
Слайд 56ТАБЛИЦА ИСТИННОСТИ БУЛЕВОЙ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
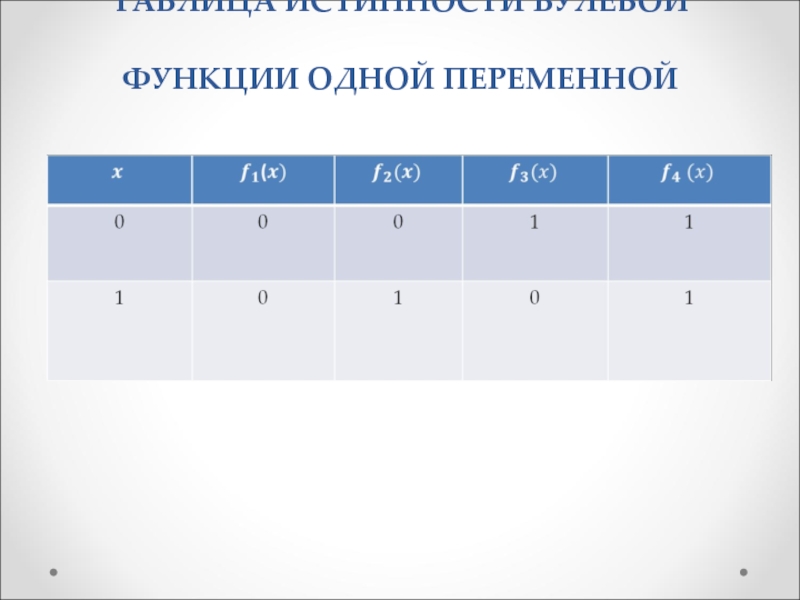
Слайд 57ТАБЛИЦА ИСТИННОСТИ БУЛЕВОЙ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Слайд 62Свойства элементарных булевых функций
1. Функции: конъюнкция, дизъюнкция, сумма по модулю
два, стрелка Пирса, штрих Шеффера коммутативны.
2. Функции: конъюнкция, дизъюнкция, сумма
по модулю два ассоциативны и дистрибутивны.
Слайд 63Свойства элементарных булевых функций
Слайд 64Свойства элементарных булевых функций
Слайд 65Свойства элементарных булевых функций
Слайд 66Cвойства элементарных булевых функций
Слайд 70Алгоритм построения КНФ И ДНФ
3) Избавиться от знаков двойного
отрицания.
4) Применить к операциям конъюнкции и дизъюнкции свойства дистрибутивности и
формулы поглощения.
Слайд 71Совершенная конъюктивная нормальная форма
Совершенной конъюктивной нормальной формой (СКНф) называется такая
её КНФ, которая удовлетворяет следующим свойствам:
1) КНФ не
содержит двух одинаковых дизъюнкций.
2) Ни одна из дизъюнкций не содержит одновременно двух одинаковых переменных.
3) Ни одна из дизъюнкций не содержит одновременно некоторую переменную и её отрицание.
Слайд 72Совершенная конъюктивная нормальная форма
Слайд 73Совершенная дизъюнктивная нормальная форма
Совершенной дизъюнктивной нормальной формой (СДНФ) называется её
ДНФ, обладающая свойствами:
1) ДНФ не содержит двух одинаковых конъюнкций.
2) Ни
одна конъюнкция не содержит одновременно двух одинаковых переменных.
Слайд 75Совершенная дизъюнктивная нормальная форма
Слайд 78Основные понятия теории графов. Степень вершины, маршруты, цепи, циклы.
Лекция 6
Слайд 79ПОНЯТИЕ ГРАФА
Графом называют совокупность объектов со связями между ними или
граф -
непустое конечное множество вершин (узлов) и множество ребер (дуг) , оба конца которых принадлежат множеству
Объекты – множество вершин
Связи – множество ребер
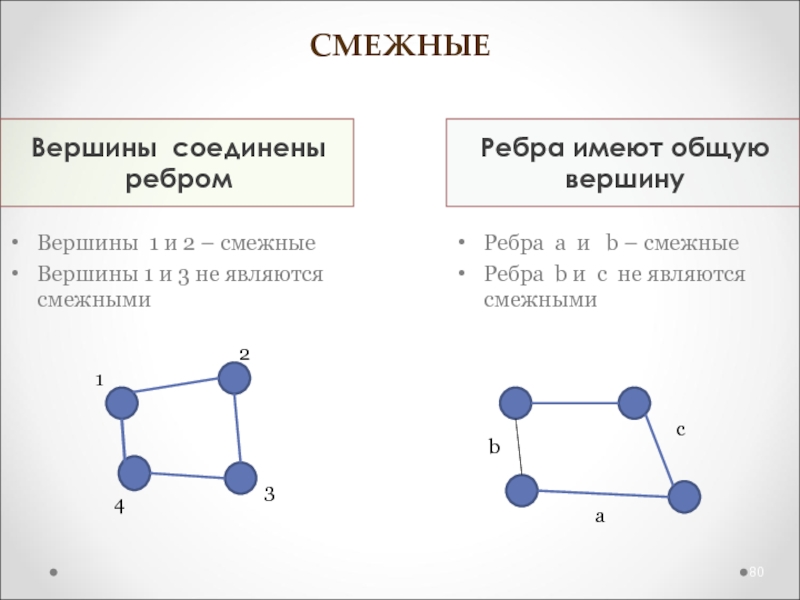
Слайд 80СМЕЖНЫЕ
Вершины соединены ребром
Ребра имеют общую вершину
Вершины 1 и 2 –
смежные
Вершины 1 и 3 не являются смежными
Ребра a и
b – смежные
Ребра b и c не являются смежными
1
2
3
4
a
b
c
Слайд 81
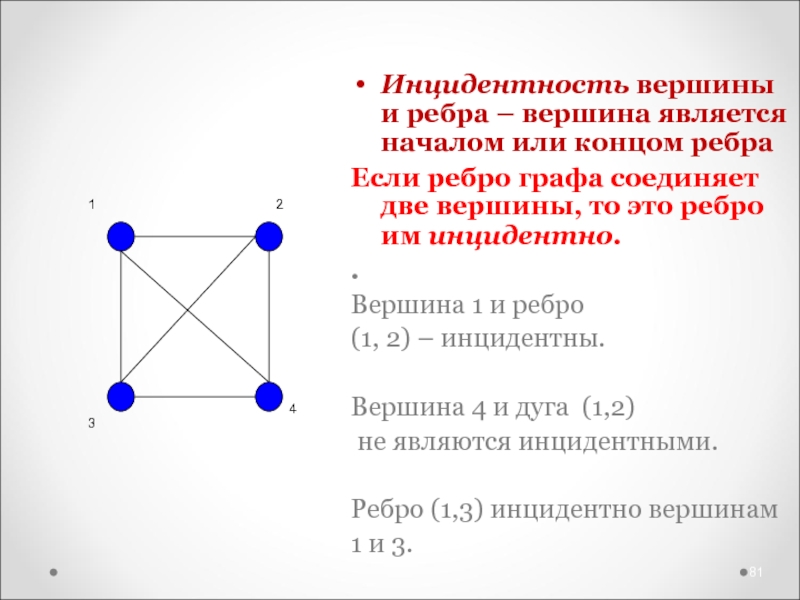
Инцидентность вершины и ребра – вершина является началом или концом
ребра
Если ребро графа соединяет две вершины, то это ребро им
инцидентно.
.
Вершина 1 и ребро
(1, 2) – инцидентны.
Вершина 4 и дуга (1,2)
не являются инцидентными.
Ребро (1,3) инцидентно вершинам
1 и 3.
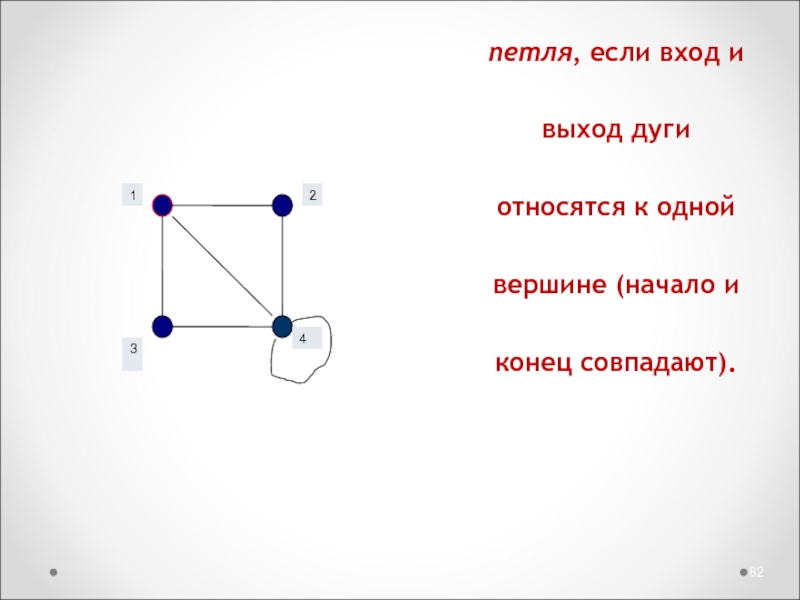
Слайд 82Дуга (ребро )– петля, если вход и выход дуги относятся
к одной вершине (начало и конец совпадают).
Слайд 83Мультиграф
- это граф, в котором пара вершин соединяется несколькими ребрами
Слайд 84Степень вершины -
Это число ребер, инцидентных вершине.
Если вершине инцидентна
петля, то она дает вклад в степень, равный 2 (два
конца входят в одну вершину)
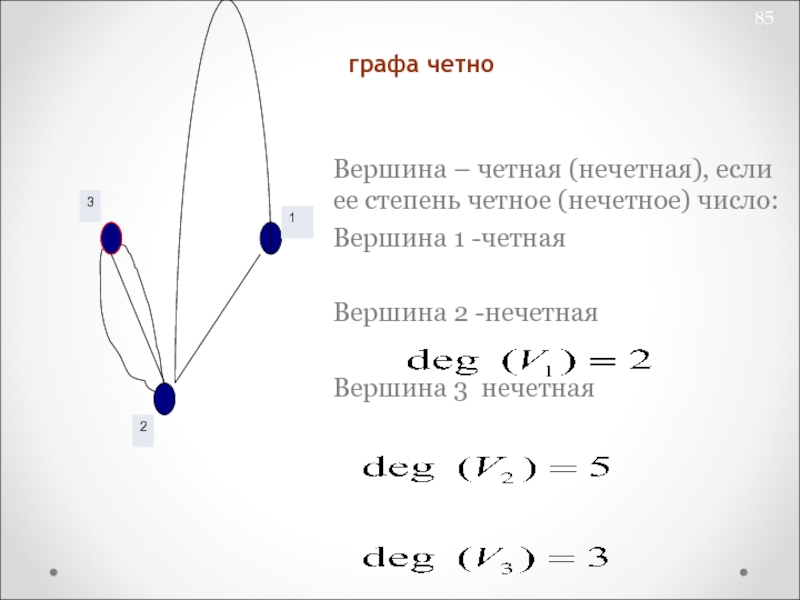
Слайд 85Четность вершин: число нечетных вершин любого графа четно
Вершина – четная
(нечетная), если ее степень четное (нечетное) число:
Вершина 1 -четная
Вершина 2
-нечетная
Вершина 3 нечетная
Слайд 86Сумма степеней всех вершин графа -четное число, равное удвоенному числу
ребер графа
Число вершин графа
Число ребер графа
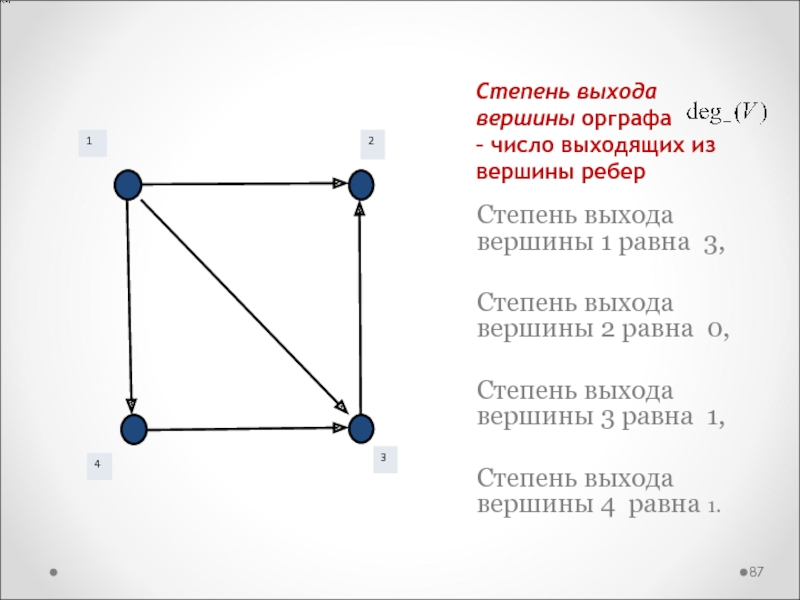
Слайд 87Степень выхода вершины орграфа
– число выходящих из вершины ребер
Степень выхода вершины 1 равна
3,
Степень выхода вершины 2 равна 0,
Степень выхода вершины 3 равна 1,
Степень выхода вершины 4 равна 1.
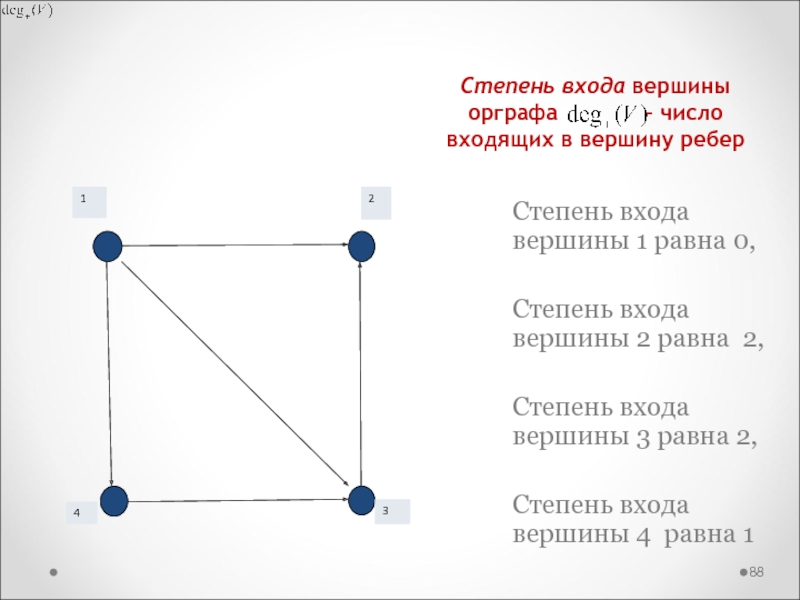
Слайд 88Степень входа вершины орграфа
– число входящих в вершину ребер
Степень входа вершины 1 равна
0,
Степень входа вершины 2 равна 2,
Степень входа вершины 3 равна 2,
Степень входа вершины 4 равна 1
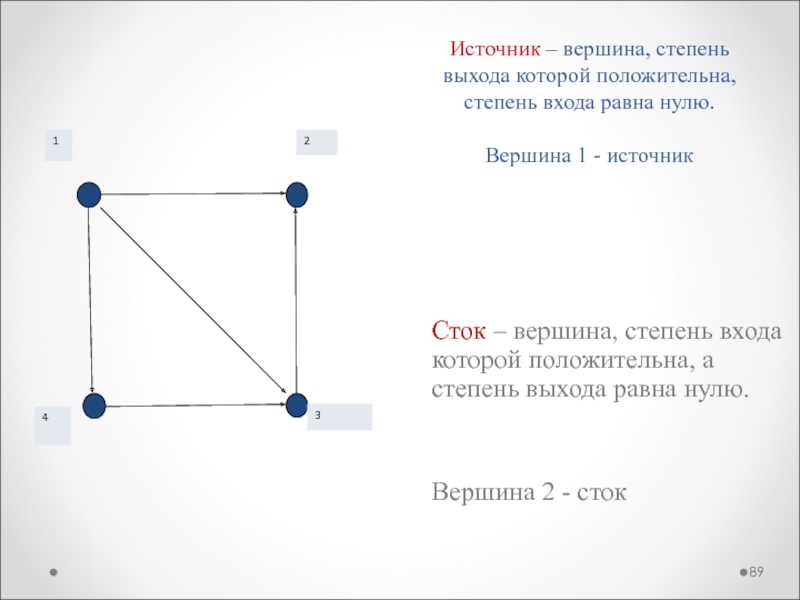
Слайд 89Источник – вершина, степень выхода которой положительна, степень входа равна
нулю.
Вершина 1 - источник
Сток – вершина, степень входа которой положительна,
а степень выхода равна нулю.
Вершина 2 - сток
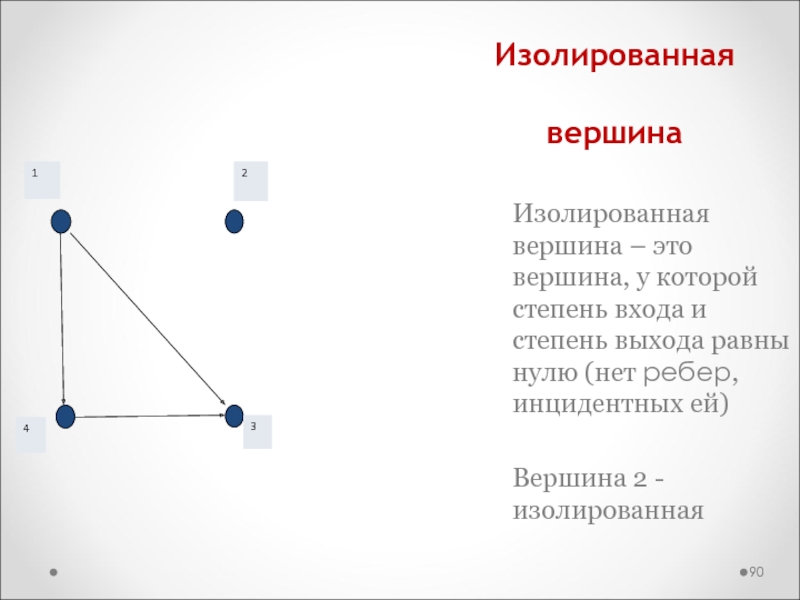
Слайд 90Изолированная вершина
Изолированная вершина – это вершина, у которой степень входа
и степень выхода равны нулю (нет ребер, инцидентных ей)
Вершина 2
- изолированная
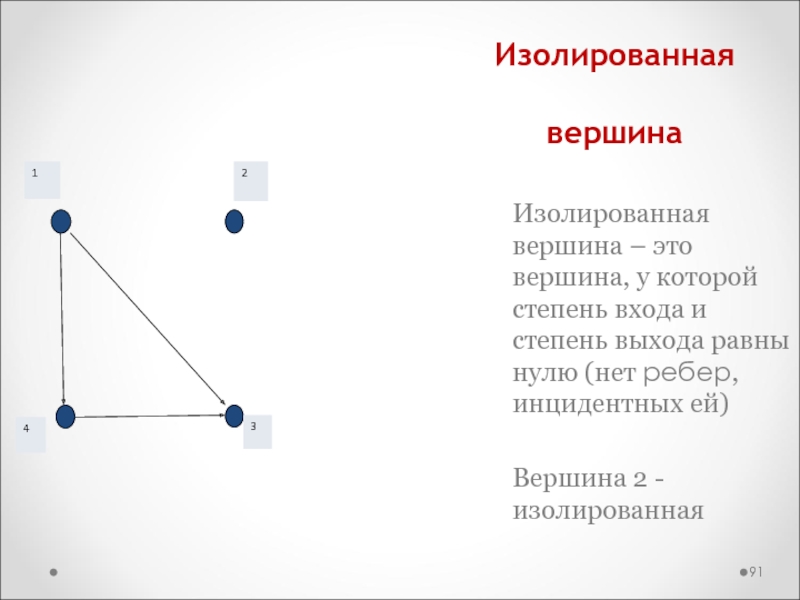
Слайд 91Изолированная вершина
Изолированная вершина – это вершина, у которой степень входа
и степень выхода равны нулю (нет ребер, инцидентных ей)
Вершина 2
- изолированная
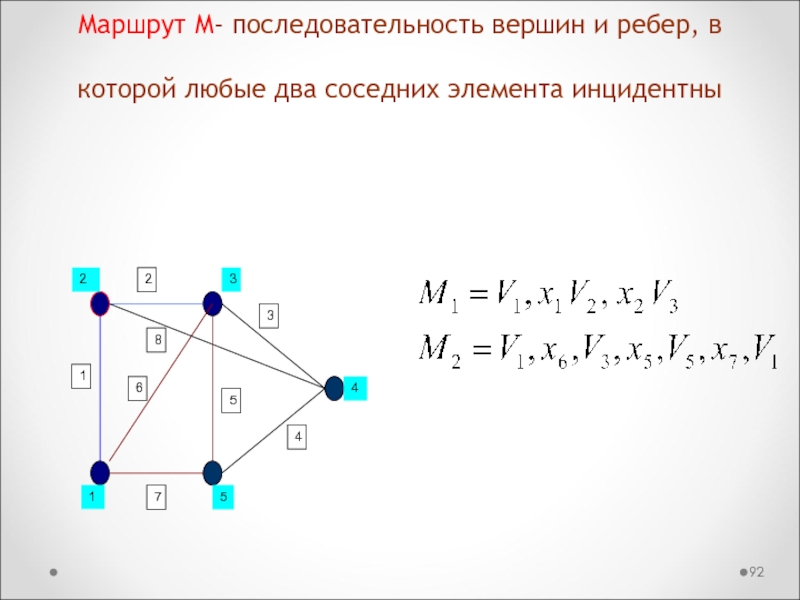
Слайд 92Маршрут М- последовательность вершин и ребер, в которой любые два
соседних элемента инцидентны
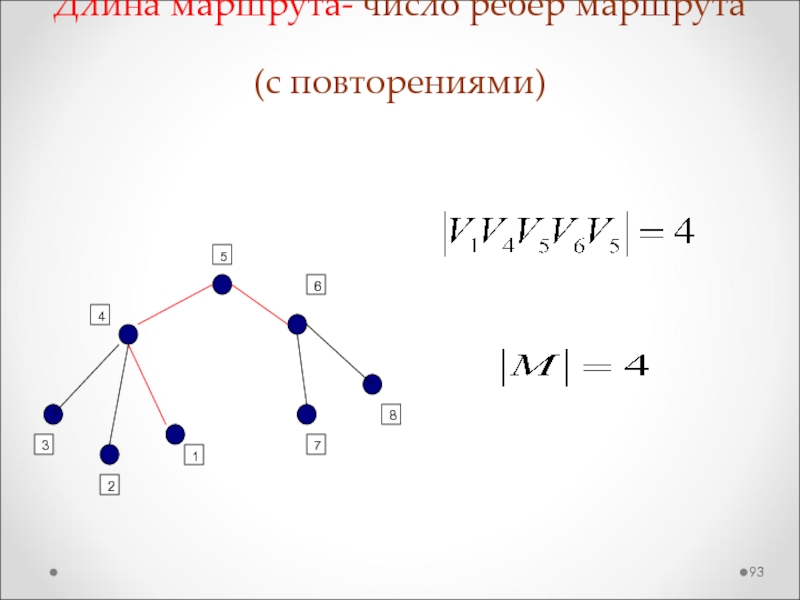
Слайд 93Длина маршрута- число ребер маршрута
(с повторениями)
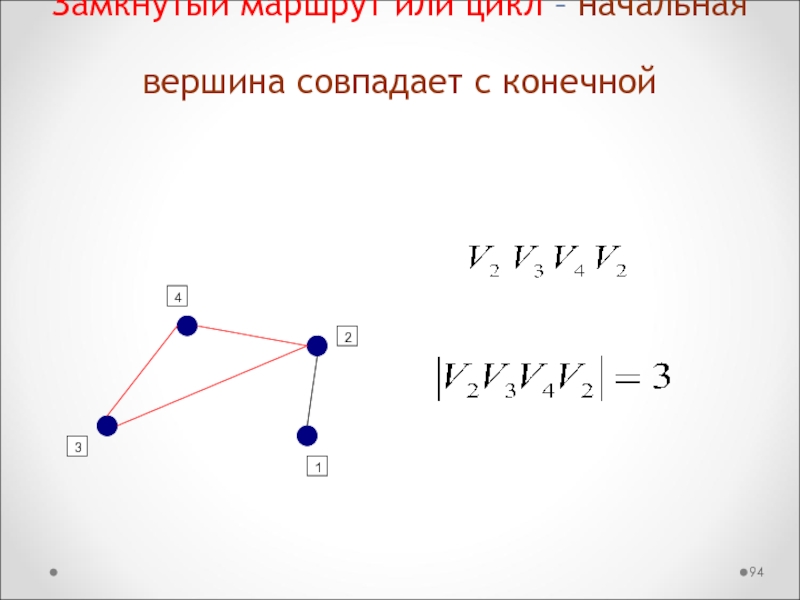
Слайд 94Замкнутый маршрут или цикл – начальная вершина совпадает с конечной
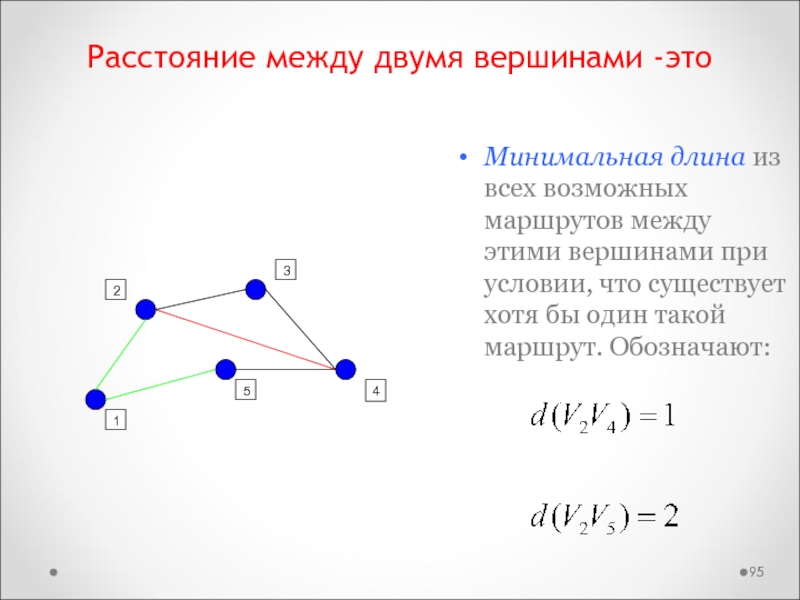
Слайд 95Расстояние между двумя вершинами -это
Минимальная длина из всех возможных маршрутов
между этими вершинами при условии, что существует хотя бы один
такой маршрут. Обозначают:
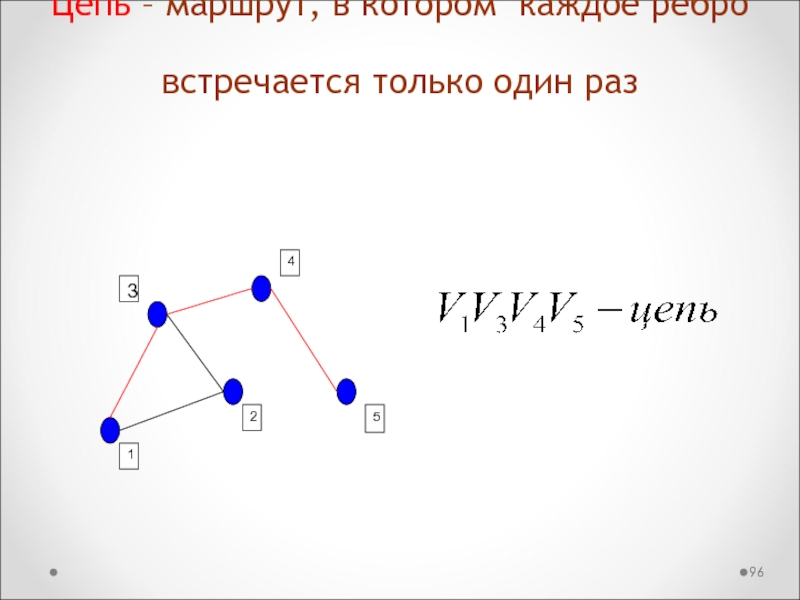
Слайд 96Цепь – маршрут, в котором каждое ребро встречается только один
раз
Слайд 97Ориентированные графы. Изоморфизм графов. Операции над графами.
Лекция 7
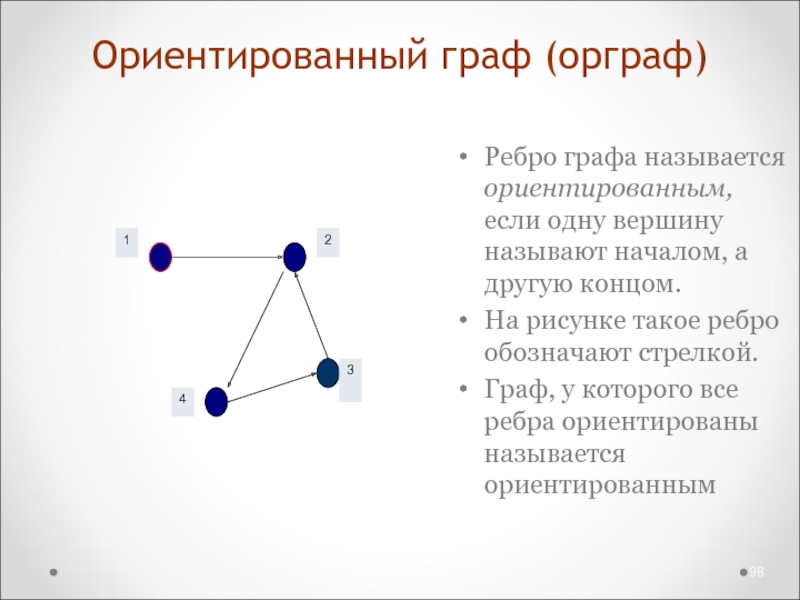
Слайд 98Ориентированный граф (орграф)
Ребро графа называется ориентированным, если одну вершину называют
началом, а другую концом.
На рисунке такое ребро обозначают стрелкой.
Граф, у
которого все ребра ориентированы называется ориентированным
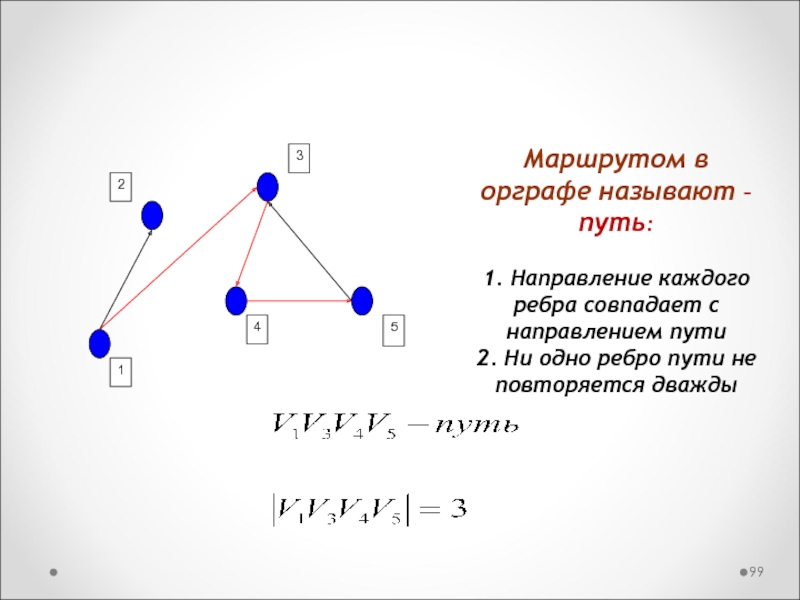
Слайд 99Маршрутом в орграфе называют – путь:
1. Направление каждого ребра совпадает
с направлением пути
2. Ни одно ребро пути не повторяется дважды
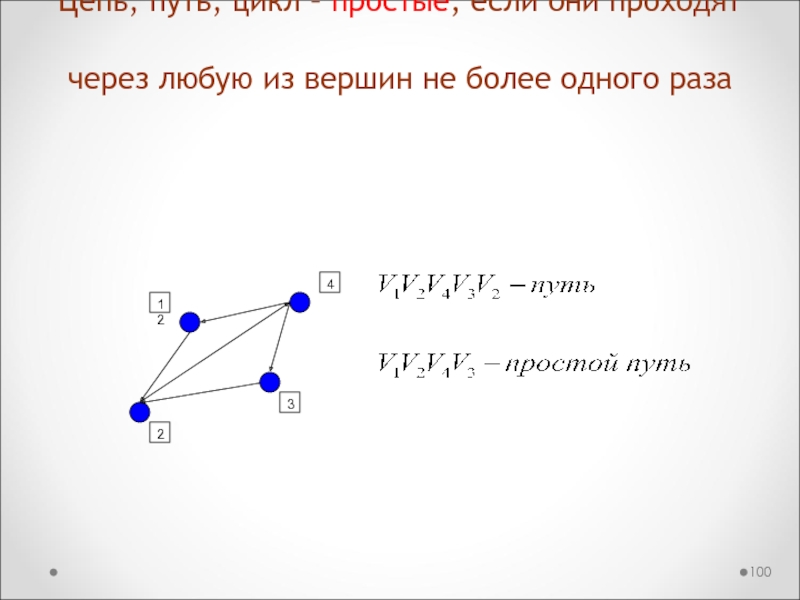
Слайд 100Цепь, путь, цикл – простые, если они проходят через любую
из вершин не более одного раза
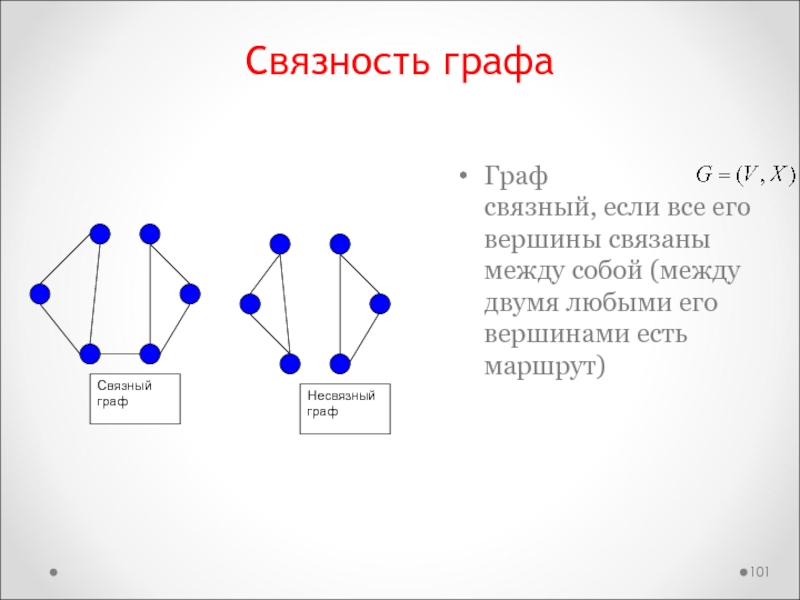
Слайд 101Связность графа
Граф
связный, если все его вершины связаны между
собой (между двумя любыми его вершинами есть маршрут)
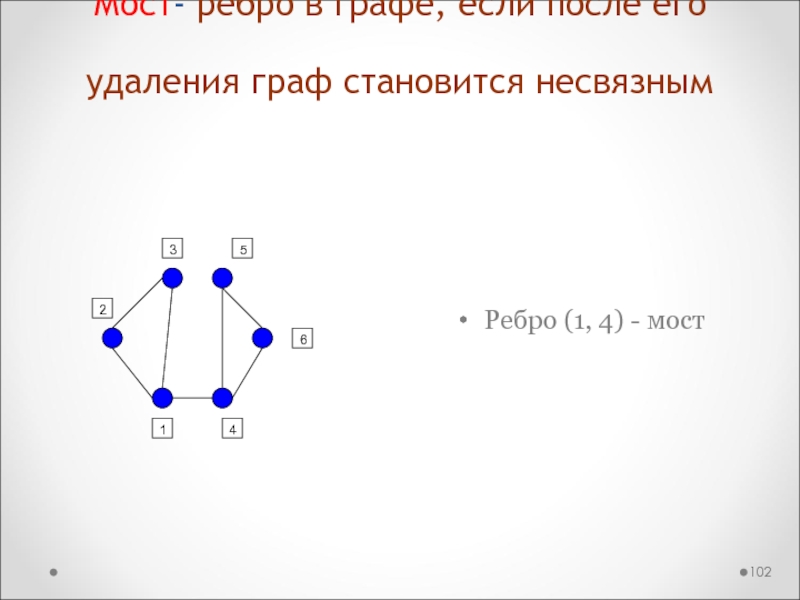
Слайд 102Мост- ребро в графе, если после его удаления граф становится
несвязным
Ребро (1, 4) - мост
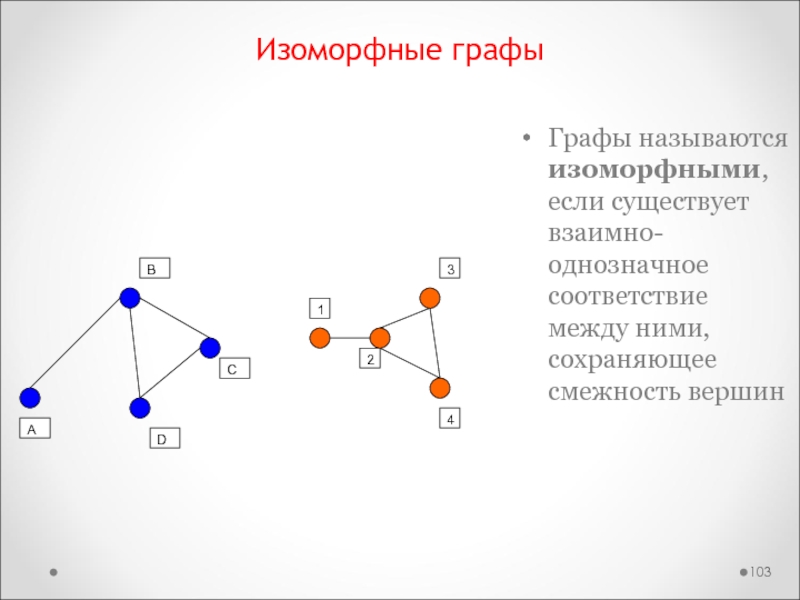
Слайд 103Изоморфные графы
Графы называются изоморфными, если существует взаимно-однозначное соответствие между ними,
сохраняющее смежность вершин
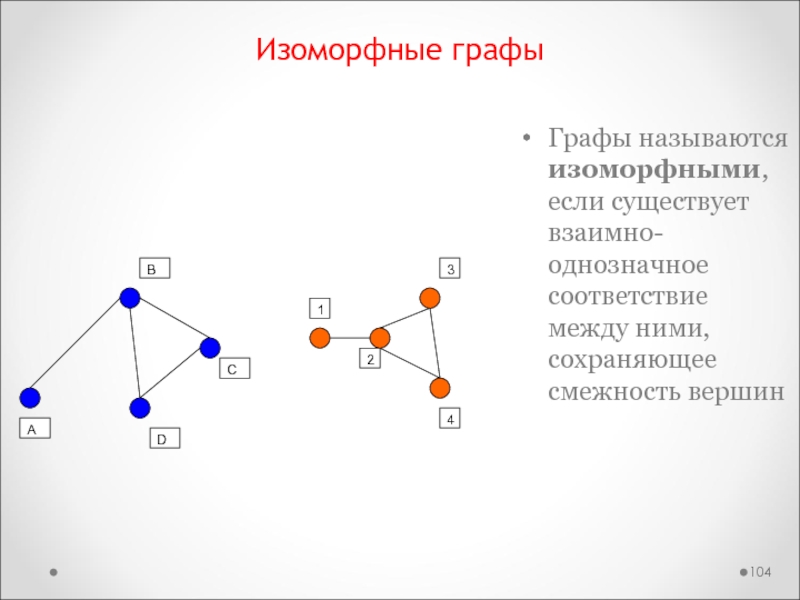
Слайд 104Изоморфные графы
Графы называются изоморфными, если существует взаимно-однозначное соответствие между ними,
сохраняющее смежность вершин
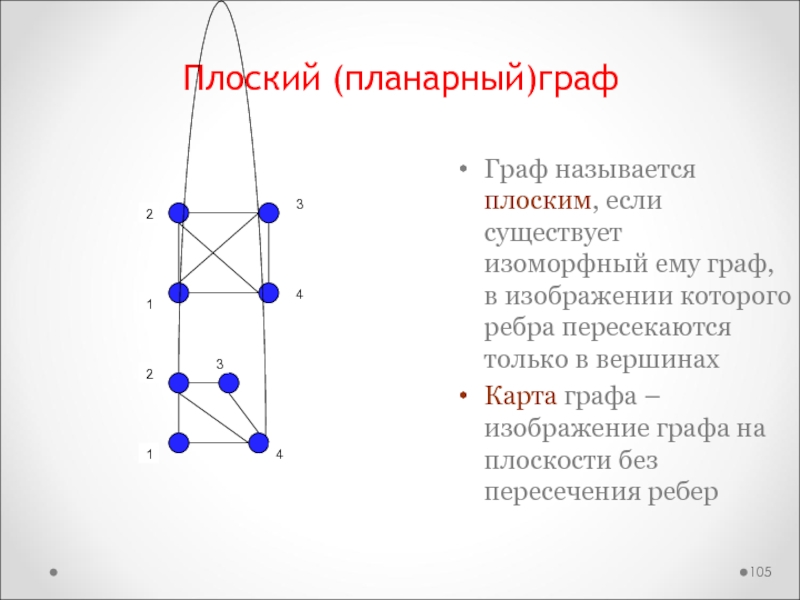
Слайд 105Плоский (планарный)граф
Граф называется плоским, если существует изоморфный ему граф,
в изображении которого ребра пересекаются только в вершинах
Карта графа –
изображение графа на плоскости без пересечения ребер
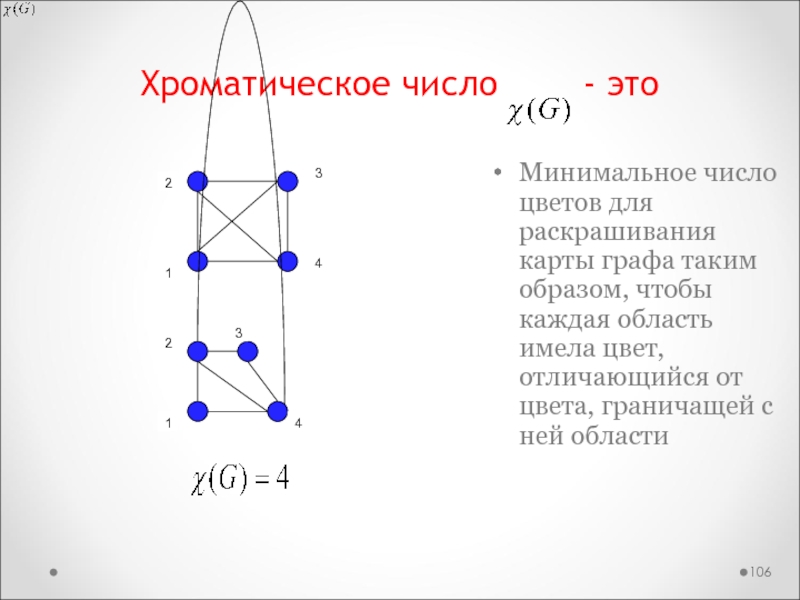
Слайд 106Хроматическое число - это
Минимальное число цветов для
раскрашивания карты графа таким образом, чтобы каждая область имела цвет,
отличающийся от цвета, граничащей с ней области
Слайд 107Связный плоский граф с n вершинами и m ребрами разбивает
плоскость на r областей (включая внешнюю). При этом справедливо:
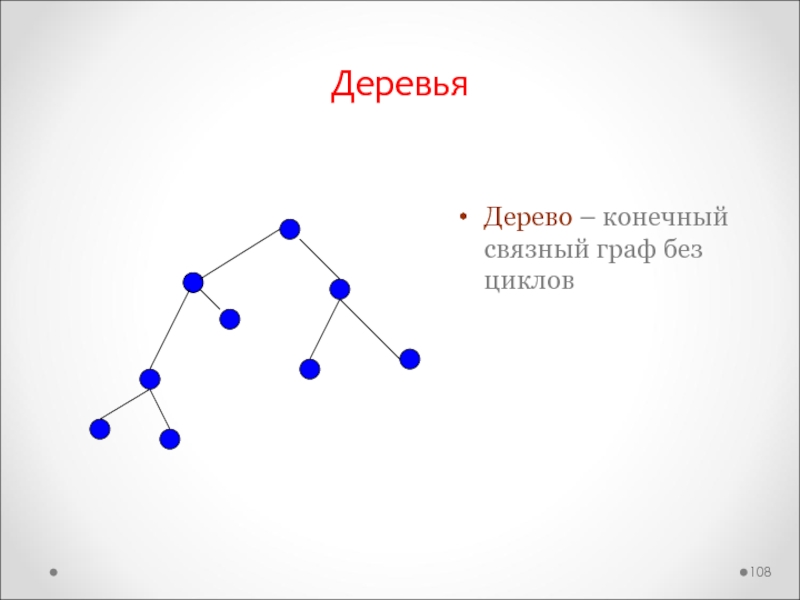
Слайд 108Деревья
Дерево – конечный связный граф без циклов
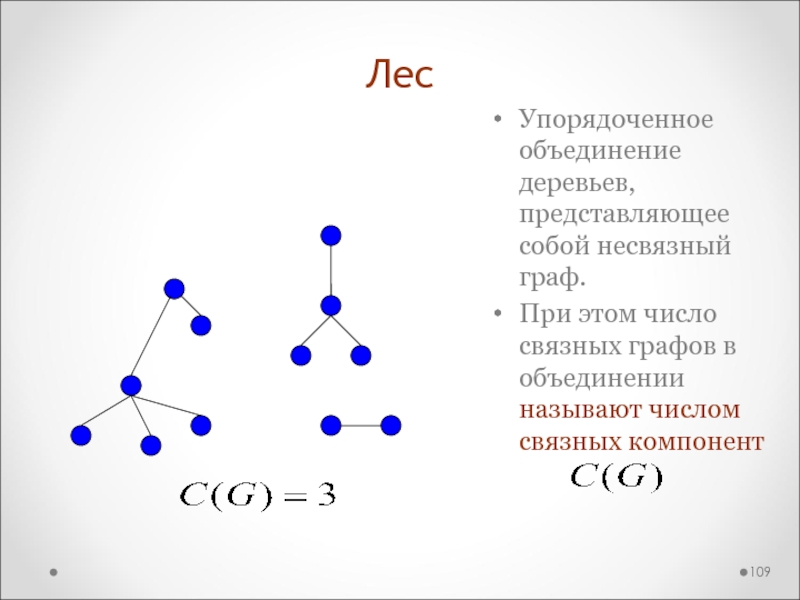
Слайд 109Лес
Упорядоченное объединение деревьев, представляющее собой несвязный граф.
При этом число
связных графов в объединении называют числом связных компонент
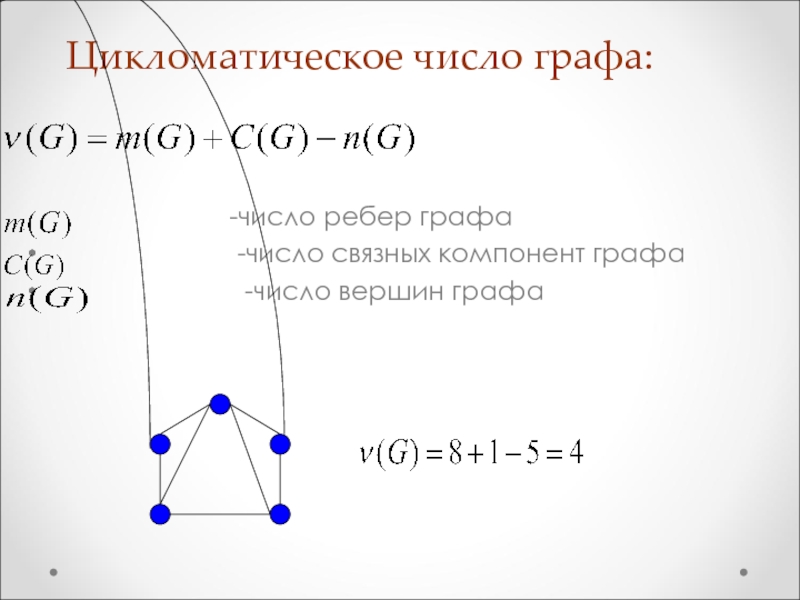
Слайд 110Цикломатическое число графа:
-число ребер графа
-число связных компонент графа
-число вершин графа
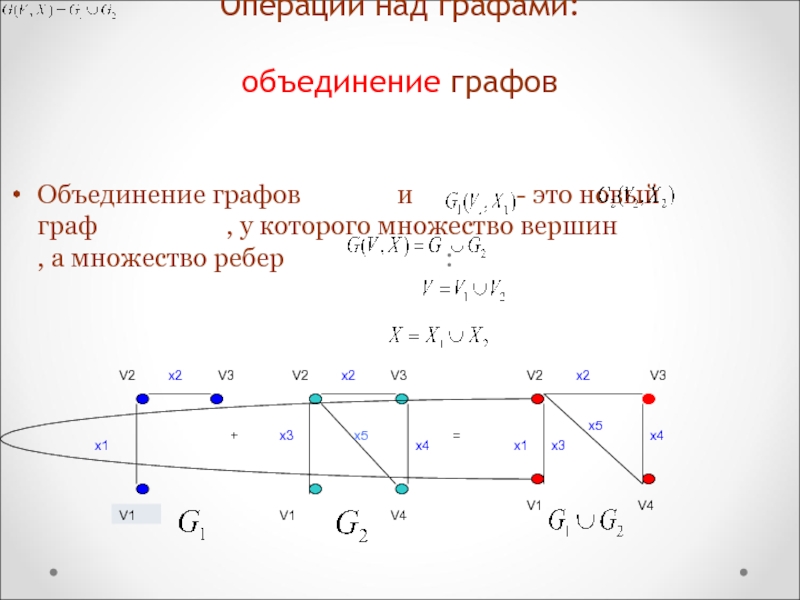
Слайд 111Операции над графами:
объединение графов
Объединение графов
и
- это новый граф , у которого множество вершин , а множество ребер :
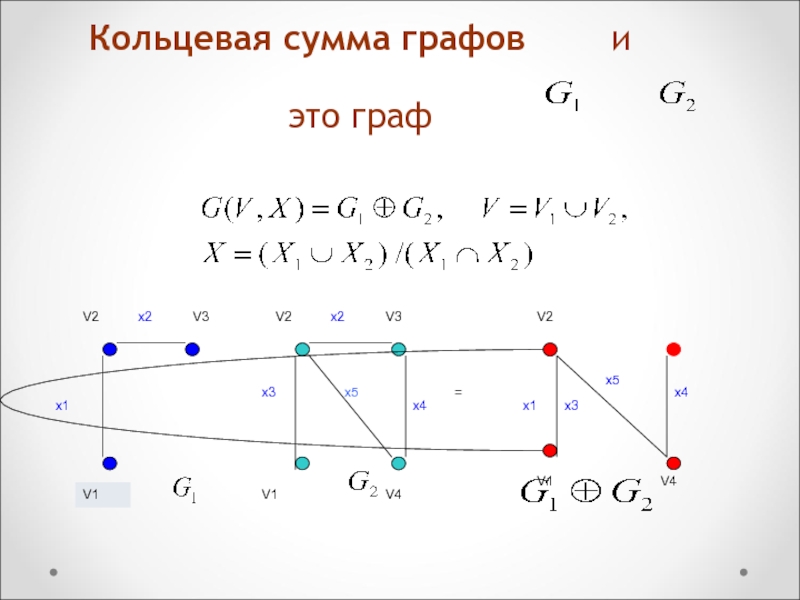
Слайд 112Операции над графами:
пересечение графов
Пересечение графов и
- это
граф, для которого - множество вершин, а - множество ребер
Слайд 114Способы задания графов. Матрицы смежности, инцидентности графов.
Лекция 8
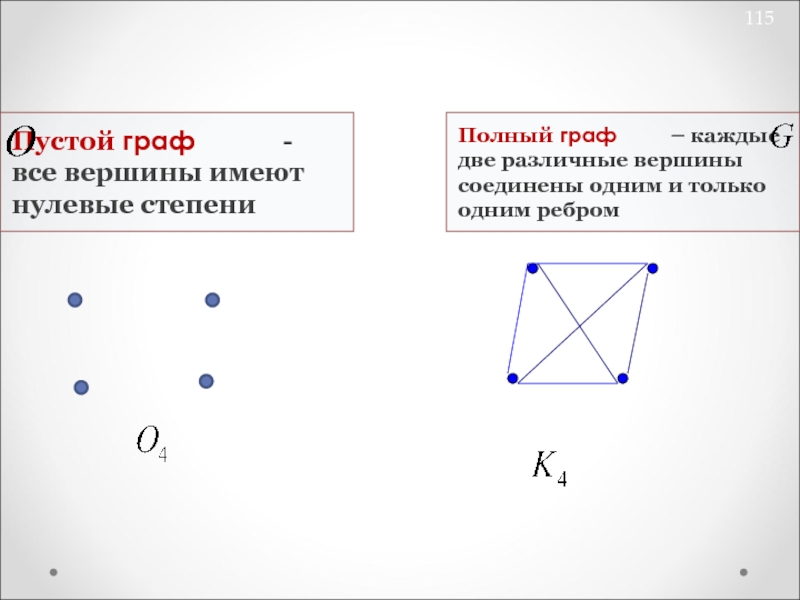
вершины имеют нулевые степени
Полный граф –
каждые две различные вершины соединены одним и только одним ребром
Слайд 116Дополнение графа –это другой граф
, с теми же вершинами, что и данный
граф и ребрами, которые надо добавить к первому графу, чтобы получился полный граф
Слайд 117МАТРИЦА ИНЦИДЕНТНОСТИ
Матрица инцидентности графа G с конечным числом
вершин n и числом ребер —
это прямоугольная матрица B размерности
Слайд 118МАТРИЦА ИНЦИДЕНТНОСТИ
Матрицей инцидентности орграфа называется прямоугольная матрица
размерности
- число вершин, -
число ребер.
Элемент матрицы принимает значение 1, если вершина – начало ребра,
Элемент матрицы принимает значение -1 , если вершина – конец ребра
Элемент равен 2, если у вершины есть петля
Элемент равен 0, если вершина не инцидентна ребру
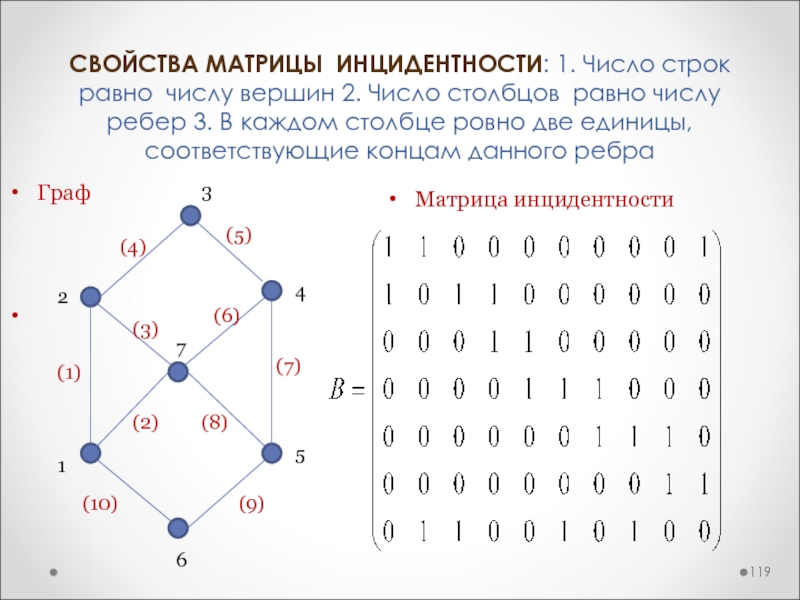
Слайд 119СВОЙСТВА МАТРИЦЫ ИНЦИДЕНТНОСТИ: 1. Число строк равно числу вершин 2.
Число столбцов равно числу ребер 3. В каждом столбце ровно
две единицы, соответствующие концам данного ребра
Граф
Матрица инцидентности
1
2
3
4
5
6
7
(1)
(3)
(2)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
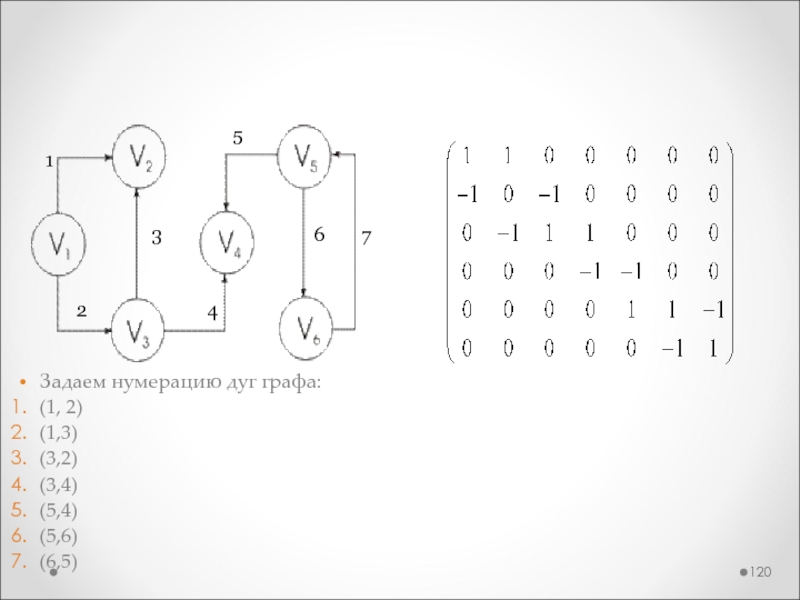
МАТРИЦА ИНЦИДЕНТНОСТИ
Задаем нумерацию дуг графа:
(1, 2)
(1,3)
(3,2)
(3,4)
(5,4)
(5,6)
(6,5)
1
2
4
3
5
6
7
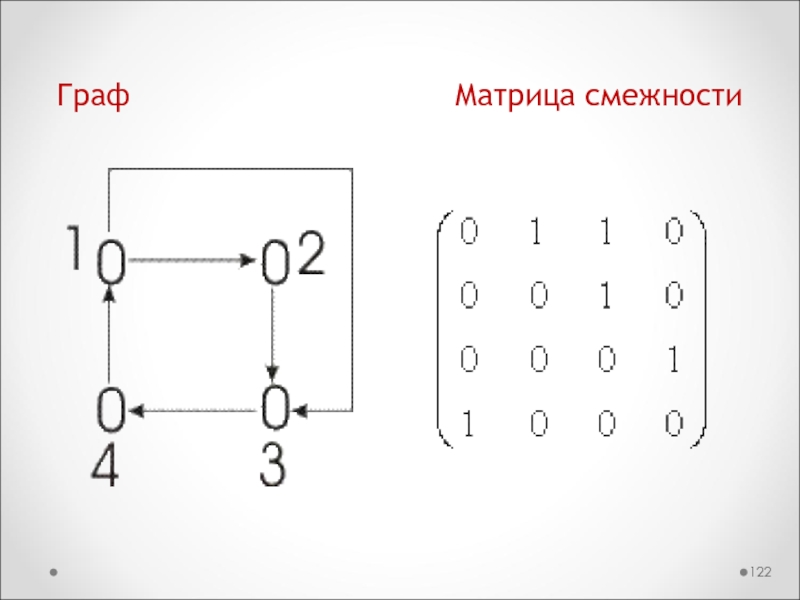
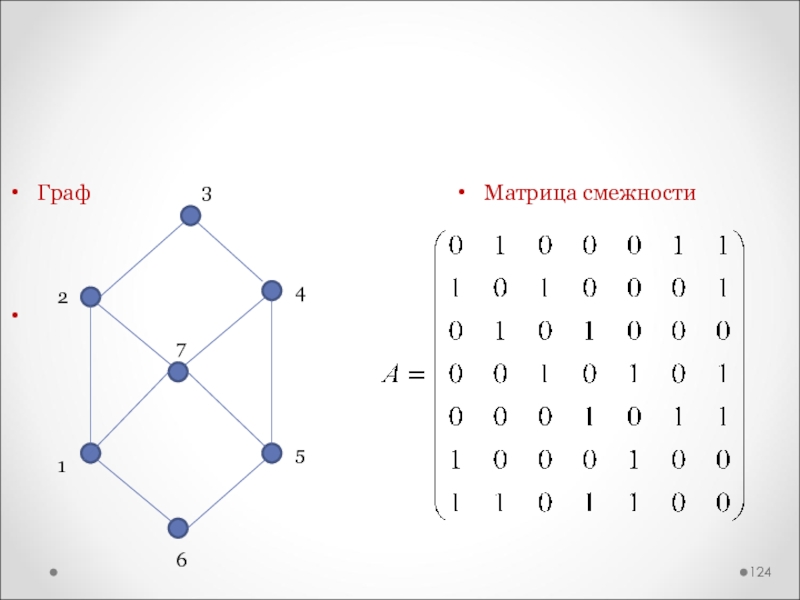
Слайд 121МАТРИЦА СМЕЖНОСТИ ГРАФА
Матрица смежности графа G с конечным числом вершин
n (пронумерованных числами от 1 до n) — это квадратная
матрица A порядка n, в которой значение элемента aij равно числу ребер из i-й вершины графа в j-ю вершину.