Разделы презентаций

Способы преобразования проекций

Содержание

Способ вращенияСпособ вращения базируется на следующих основных положениях:при вращении вокруг некоторой неподвижной прямой (оси вращения) каждая точка вращаемой фигуры перемещается в плоскости, перпендикулярной оси вращения;каждая точка вращаемой фигуры перемещается по окружности,

Слайды и текст этой презентации

Слайд 1Способы преобразования проекций
- изменить положение в пространстве рассматриваемого геометрического элемента

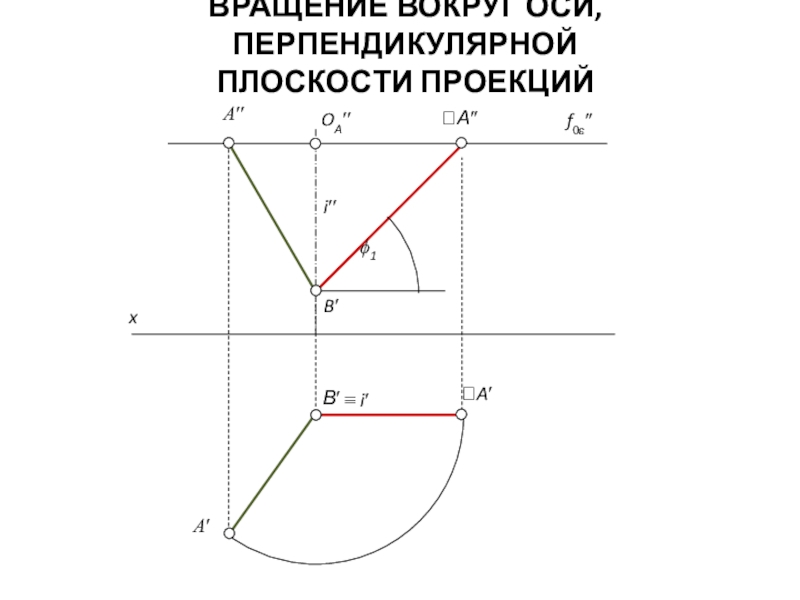
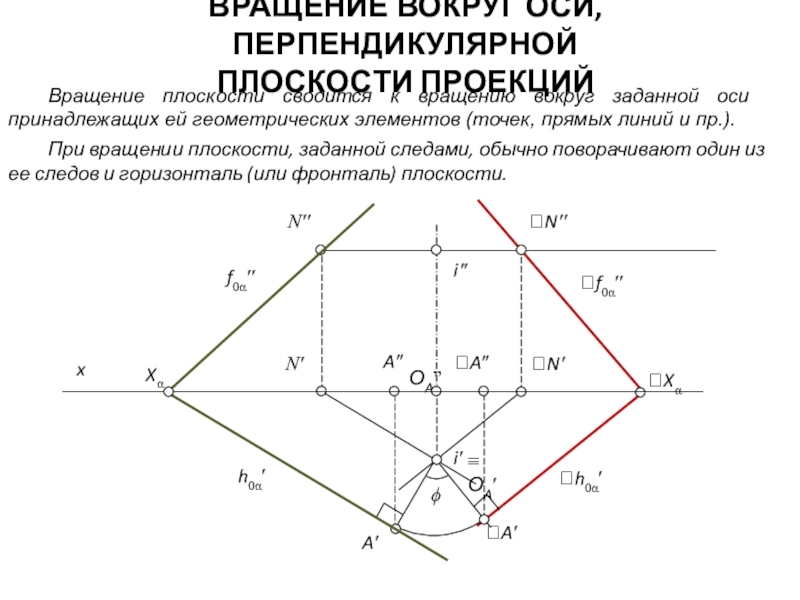
путем его вращения вокруг одной или нескольких осей, оставив неизменным

положение плоскостей проекций;

- ввести одну или несколько дополнительных плоскостей проекций, оставив неизменным положение геометрического элемента.

Преобразовать проекции можно следующими способами:

Способы преобразования проекций- изменить положение в пространстве рассматриваемого геометрического элемента путем его вращения вокруг одной или нескольких

Слайд 2Способ вращения
Способ вращения базируется на следующих основных положениях:
при вращении вокруг

некоторой неподвижной прямой (оси вращения) каждая точка вращаемой фигуры перемещается

в плоскости, перпендикулярной оси вращения;

каждая точка вращаемой фигуры перемещается по окружности, центр которой (центр вращения) находится в точке пересечения оси с плоскостью вращения;

радиус вращения равен кратчайшему расстоянию от вращаемой точки до оси вращения;

точки, расположенные на оси вращения, своего положения в пространстве не изменяют.

Способ вращенияСпособ вращения базируется на следующих основных положениях:при вращении вокруг некоторой неподвижной прямой (оси вращения) каждая точка

Слайд 3Вращение вокруг оси, перпендикулярной
плоскости проекций
h0
ОA 
i
ОA

А
А
ОА 

ОА


i
RA
OA


i
i

Вращение вокруг оси, перпендикулярной плоскости проекцийh0ОA  iОAААОА ОАiRAOAii

Слайд 4Вращение вокруг оси, перпендикулярной
плоскости проекций
Для вращения отрезка АВ вокруг

оси, перпендикулярной плоскости 1, на некоторый угол  нужно

повернуть на этот угол любые две его точки

f02

f01

OA

OB

B

А



RА

B

RB

 OA  OB

Вращение вокруг оси, перпендикулярной плоскости проекцийДля вращения отрезка АВ вокруг оси, перпендикулярной плоскости 1, на некоторый угол

Слайд 5OA
f0
A
А
i


Вращение вокруг оси, перпендикулярной
плоскости проекций
 i

OA f0 AА i Вращение вокруг оси, перпендикулярной плоскости проекций i

Слайд 6Вращение вокруг оси, перпендикулярной
плоскости проекций
Вращение плоскости сводится к вращению

вокруг заданной оси принадлежащих ей геометрических элементов (точек, прямых линий

и пр.).

При вращении плоскости, заданной следами, обычно поворачивают один из ее следов и горизонталь (или фронталь) плоскости.

i

h0

f0

X

N

N

N

N

A

A


A

A

 ОА

ОА”

Вращение вокруг оси, перпендикулярной плоскости проекций Вращение плоскости сводится к вращению вокруг заданной оси принадлежащих ей геометрических элементов

Слайд 7Вращение вокруг оси, перпендикулярной
плоскости проекций
Пример : Определить угол наклона

плоскости общего положения , заданной следами к горизонтальной плоскости проекций


Вращение вокруг оси, перпендикулярной плоскости проекцийПример : Определить угол наклона плоскости общего положения , заданной следами к

Слайд 8Пример : Определить истинную величину треугольника АВС
Вращение вокруг оси, перпендикулярной


плоскости проекций
Для определения истинной величины треугольника АВС повернем его дважды:

сначала в положение, перпендикулярное плоскости 2, а затем в положение, параллельное плоскости 1. Тогда в итоге на горизонтальную плоскость проекций треугольник спроецируется без искажения.
Пример : Определить истинную величину треугольника АВСВращение вокруг оси, перпендикулярной плоскости проекцийДля определения истинной величины треугольника АВС

Слайд 9A
f0A
h0C
A
1
B
1
B
B
1
f0B
i1
h0B
i2
C
B
 i1
 i2
C

A f0A h0CA1B1BB1 f0B i1 h0Bi2CB i1 i2C

Похожие презентации

Терморегуляция ПГТУ.ppt Терморегуляция ПГТУ.ppt 279
Тема : Искусство символизма (живопись) Тема : Искусство символизма (живопись) 254
5 2 6 Влияние факторов.ppt 5 2 6 Влияние факторов.ppt 257
Концепция опасной профессии. Концепция опасной профессии Концепция опасной профессии. Концепция опасной профессии 423
Феминизм Феминизм 244
Социальные сети как средство социального воспитания подростков МИНИСТЕРСТВО Социальные сети как средство социального воспитания подростков МИНИСТЕРСТВО 549
Муниципальное бюджетное образовательное учреждение дополнительного образования Муниципальное бюджетное образовательное учреждение дополнительного образования 199
Коммерческое предложение на примере Школы воздушного танца My Aerial Dance Коммерческое предложение на примере Школы воздушного танца My Aerial Dance 245
Насекомые Насекомые 314
Алматы Технологиялық Университеті ТақырыбЫ:Сомалық гибридизацияны практикада Алматы Технологиялық Университеті ТақырыбЫ:Сомалық гибридизацияны практикада 292
Чередование гласных в корнях слов Чередование гласных в корнях слов 206
Системный анализ Системный анализ 186
Есть ли смысл в его показах и в его сегодняшних словах? Товкес Анна Есть ли смысл в его показах и в его сегодняшних словах? Товкес Анна 314
Организация работы молочной кухни Организация работы молочной кухни 244
November 2011 Confidential Fleming Family and Partners Asset Management LLC November 2011 Confidential Fleming Family and Partners Asset Management LLC 203
Химия и производство. Химическая промышленность и химические Химия и производство. Химическая промышленность и химические 152
Стационарный режим в СМО Стационарный режим в СМО 336
(по книге Алиса в стране чудес) Мир парадоксов и абсурда Нижний Тагил, МБОУ (по книге Алиса в стране чудес) Мир парадоксов и абсурда Нижний Тагил, МБОУ 442
“ АСТАНА МЕДИЦИНА УНИВЕРСИТЕТІ ” АҚ “ АСТАНА МЕДИЦИНА УНИВЕРСИТЕТІ ” АҚ 467
Периодическая система химических элементов Д.И. Менделеева Периодическая система химических элементов Д.И. Менделеева 353

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика