Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статика
Содержание
- 1. Статика
- 2. Некоторые определения и понятия статикиСистема сил называется
- 3. Задачи, решаемые в рамках статикиОпределение условий равновесия
- 4. Составляющие вектора силыСоставляющими вектора силы Называют векторы
- 5. РычагиРычаг 1 рода – имеет точку опоры между усилием и нагрузкойF
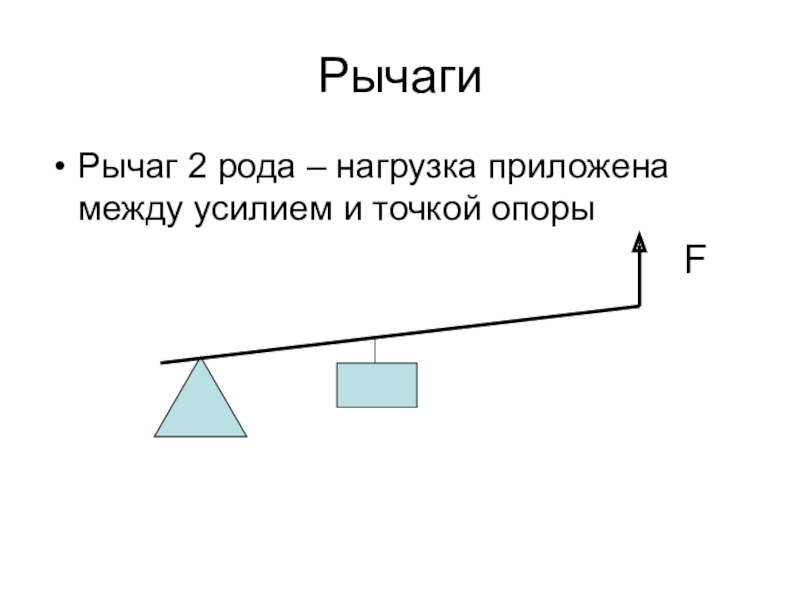
- 6. РычагиРычаг 2 рода – нагрузка приложена между усилием и точкой опорыF
- 7. РычагиРычаг 3 рода – усилие приложено между точкой опоры и нагрузкойF
- 8. Условия равновесия материальных телУсловия равновесия материальной точкиУсловия равновесия абсолютно твердого тела, совершающего поступательное движение
- 9. Условия равновесия материальных телУсловия равновесия твердого тела, имеющего закрепленную ось вращенияУсловия равновесия абсолютно твердого тела
- 10. Виды равновесияУстойчивое – если при любых малых
- 11. Виды равновесияНеустойчивое – если при любых малых
- 12. Виды равновесияБезразличное – если при любых малых
- 13. Механическая работаРабота постоянной силы равняется скалярному произведению
- 14. Положительная и отрицательная работа1. 2.3.
- 15. Свойства работы:работу совершает только тангенциальная составляющая силы dA
- 16. работа результирующей силы равна алгебраической сумме работ
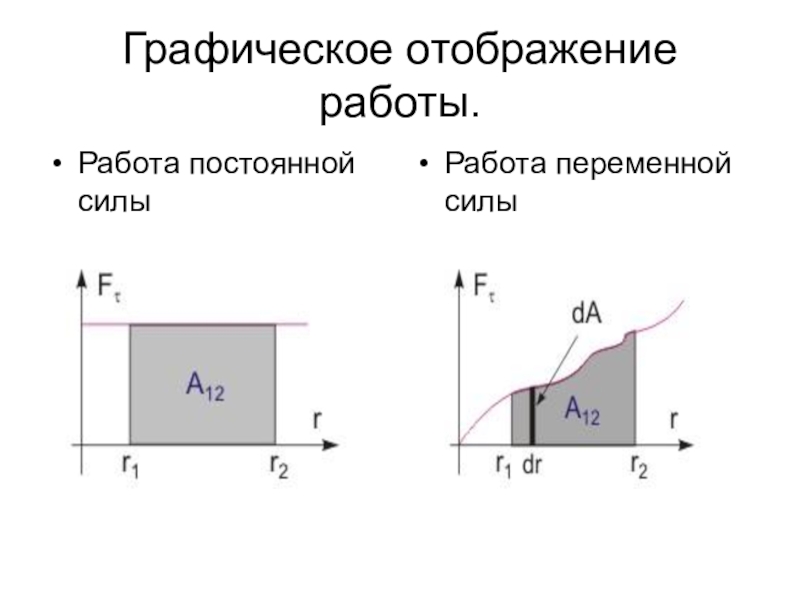
- 17. Графическое отображение работы. Работа постоянной силыРабота переменной силы
- 18. Потенциальные и непотенциальные силы Потенциальными называются такие
- 19. Консервативные и неконсервативные системы телСистема тел называется
- 20. ЭНЕРГИЯЭнергией называется скалярная физическая величина, являющаяся единой
- 21. Полная механическая энергияКинетическая энергия- характеризует движение и
- 22. Слайд 22
- 23. Теорема о кинетической энергииИзменение кинетической энергии тела
- 24. Потенциальная энергия Убыль потенциальной энергии равна
- 25. Полной механической энергией консервативной системы тел называется
- 26. Закон сохранения полной механической энергии. Полная механическая
- 27. Слайд 27
- 28. Закон сохранения полной механической энергии.Полная механическая энергия
- 29. МощностьМгновенной мощностью называется скалярная величина, равная отношению
- 30. Скачать презентанцию
Некоторые определения и понятия статикиСистема сил называется уравновешенной, если равнодействующая этой системы равна нулю.Тела, ограничивающие движение данного рассматриваемого тела, называются связями, а силы, действующие со стороны связей на данное тело, -
Слайды и текст этой презентации
Слайд 1Статика
Статика – это раздел механики , в котором изучается равновесие
материальных точек, тел и систем тел
Слайд 2Некоторые определения и понятия статики
Система сил называется уравновешенной, если равнодействующая
этой системы равна нулю.
Тела, ограничивающие движение данного рассматриваемого тела, называются
связями, а силы, действующие со стороны связей на данное тело, - силами реакции связей.
Слайд 3Задачи, решаемые в рамках статики
Определение условий равновесия тел,
Что надо сделать,
чтобы уравновесить тело или систему тел,
В каком направлении возникает движение,
если равновесие сил нарушено определенным образом.
Слайд 4Составляющие вектора силы
Составляющими вектора силы
Называют векторы силы,
сумма
которых равна данному вектору
Слайд 8Условия равновесия материальных тел
Условия равновесия материальной точки
Условия равновесия абсолютно твердого
тела, совершающего поступательное движение
Слайд 9Условия равновесия материальных тел
Условия равновесия твердого тела, имеющего закрепленную ось
вращения
Условия равновесия абсолютно твердого тела
Слайд 10Виды равновесия
Устойчивое – если при любых малых отклонения тела от
некоторого положения, допускаемого связями, возникают силы или моменты сил, стремящиеся
возвратить тело в исходное состояние.
Слайд 11Виды равновесия
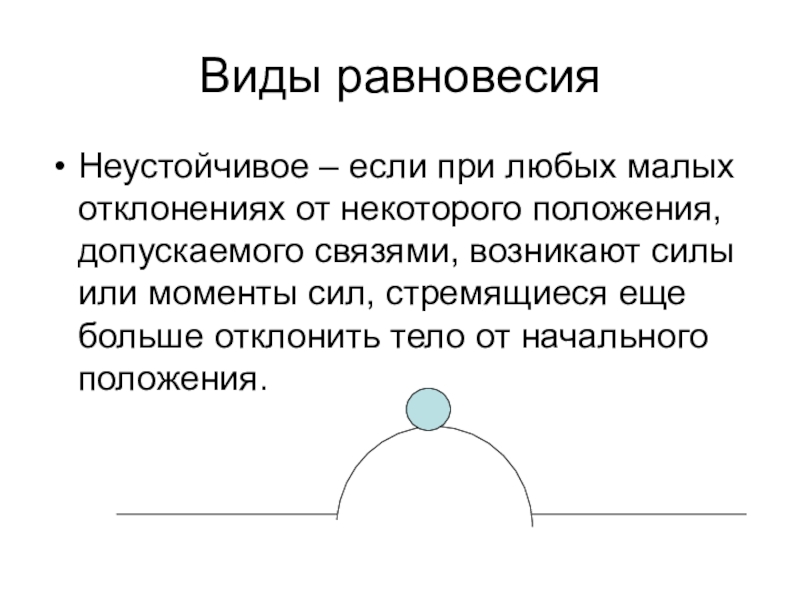
Неустойчивое – если при любых малых отклонениях от некоторого
положения, допускаемого связями, возникают силы или моменты сил, стремящиеся еще
больше отклонить тело от начального положения.
Слайд 12Виды равновесия
Безразличное – если при любых малых отклонениях тела от
некоторого положения, допускаемого связями, не возникает сил или моментов сил,
стремящихся возвратить тело в начальное положение или еще больше удалить тело от начального положения
Слайд 13Механическая работа
Работа постоянной силы равняется скалярному произведению векторов силы и
перемещения.
A1-2 = |F|·|∆r|·cos(α) = (F, ∆r).
Слайд 15Свойства работы:
работу совершает только тангенциальная составляющая силы dA = Fτ·dr. В
случае, если проекция вектора силы на тангенциальное направление больше нуля,
то сила совершает положительную работу, а если меньше нуля, то работа сил отрицательна;
Слайд 16работа результирующей силы равна алгебраической сумме работ ее составляющих.
работа
на перемещении ∆r равна сумме работ на отдельных участках траектории,
т.е. работа является аддитивной величиной.
Слайд 18Потенциальные и непотенциальные силы
Потенциальными называются такие силы, работа которых
зависит только от начального и конечного положения движущейся материальной точки
и не зависит от формы траектории (силы тяготения, упругости, электростатические).Непотенциальные – работа которых зависит от формы траектории (силы трения).
Слайд 19Консервативные и неконсервативные системы тел
Система тел называется консервативной,
если
все внутренние и внешние силы, действующие на тела системы, являются
потенциальными.Если хотя бы одно из условий консервативности нарушено, то система тел – неконсервативная.
Слайд 20ЭНЕРГИЯ
Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм
движения материи и мерой перехода движения материи из одних форм
в другиеЭнергия – способность совершить работу
Слайд 21Полная механическая энергия
Кинетическая энергия-
характеризует движение и взаимодействие тел и
является функцией скорости
Потенциальная энергия –
часть механической энергии, зависящая от
конфигурации системы, т.е. от взаимного положения ее частей во внешнем силовом поле
Слайд 23Теорема о кинетической энергии
Изменение кинетической энергии тела при переходе из
одного механического состояния в другое равно работе всех сил, действующих
на тело.
Слайд 24Потенциальная энергия
Убыль потенциальной энергии равна работе потенциальных
сил Апс, совершаемой при переходе системы из одного механического состояния
в другоеАпс = -∆Eп.
Слайд 25Полной механической энергией консервативной системы тел называется сумма ее кинетической
и потенциальной энергии:
E = Eк + Eп.Полная механическая энергия может изменяться в результате следующих причин:
внешнего воздействия на систему (толчки, приближение извне магнита, заряженных тел и т. п.);
наличия внутренних неконсервативных сил. Например, силы сопротивления вызывают уменьшение механической энергии системы.
Слайд 26Закон сохранения полной механической энергии.
Полная механическая энергия замкнутой системы,
в которой действуют только консервативные силы, не изменяется.
E = Eк + Eп=const
Слайд 28Закон сохранения полной механической энергии.
Полная механическая энергия замкнутой неконсервативной системы
равна сумме кинетической, потенциальной и внутренней энергии системы
E = Eк + Eп +U=const,где U- внутренняя энергия
Слайд 29Мощность
Мгновенной мощностью называется скалярная величина, равная отношению элементарной работы к
промежутку времени, за который она была совершена:
N = dA/dt,
где dA – элементарная работа, совершаемая силой за время dt. 
